Kraków 29.03.2012
Akademia Górniczo-Hutnicza
Im. Stanisława Staszica w Krakowie.
Wydział Inżynierii Mechanicznej i Robotyki
PODSTAWY KONSTRUKCJI MASZYN
Temat:
cz. 1: Korekcja uzębienia i zazębienia
cz. 2: Badanie sprawności przekładni zębatej.
Wykonali: Wojciech Darowski
Mateusz Dudek Krystian Dyczkowski
Mariusz Dybisiak
Łukasz Dróżdź
Gr. 3A
Część 1:
Korekcja uzębienia i zazębienia.
Cel ćwiczenia:
Poznanie istoty i skutków korekcji.
Przebieg ćwiczenia:
Specjalną kartkę papieru, na której narysowane były średnice podziałowe, średnice głów i stóp kół zębatych które poddawaliśmy analizie, zamocowaliśmy na blacie stołu stanowiska. Po przyłożeniu szablonu, obrysowywaliśmy zęby szablonu kilkanaście razy za każdym razem zmieniając nieco kąt blatu z kartką względem szablonu. Po obrysowaniu całego szablonu zaczęliśmy korygować uzębienie poprzez odsunięcie szablonu o 5 mm dla koła małego i 5mm dla koła dużego po czym ponownie obrysowywaliśmy szablon.
Znane parametry przed korekcją:
z1=9
z2=27
m=10[mm]
α=200
c=0.2
y=1
Tabela z obliczeniami:
Parametr, Wzór |
Koło Małe |
Koło Duże |
||
|
nie korygowane [mm]
|
korygowane [mm] |
nie korygowane [mm]
|
korygowane [mm] |
średnica podziałowa
|
10·9=90 |
10·9=90 |
10·27=270 |
10·27=270 |
średnica głów zęba
|
90+(2·10)=110 |
90-(2·10)=70 |
270+(2·10)=290 |
270-(2·10)=250 |
średnica stóp zęba
|
90-(2·12)=66 |
90+(2·12)=114 |
270-(2·12)=246 |
270+(2·12)=294 |
wysokość głowy zęba
|
10·(1+0+0)=10 |
10·(1+0,5+0)=15 |
10·(1+0+0)=10 |
10·(1-0,5+0)=5 |
wysokość stopy zęba
|
10·[(1-0) +0,2]=12 |
10·[(1-0,5)+0,2]=7 |
10·[(1-0) +0,2]=12 |
10·[(1+0,5)+0,2]=17 |
wysokość zęba
|
10+12=22 |
15+7=22 |
10+12=22 |
5+17=22 |
Wnioski:
- Po przeprowadzonej korekcji uzębienia, obrys stopy zęba poszerzył się, a obrys wierzchołka zwężył się.
- przy przekroczeniu wartości współczynnika przesunięcia X mogą nastąpić niekorzystne skutki korekcji uzębienia czyli nadmierne podcięcie zęba lub jego zaostrzenie.
Odpowiedzi na pytania ze skryptu:
1) Na czym polega istota korekcji P-O i kiedy można ją stosować?
Korekcje P-O można stosować gdy suma zębów w przekładni jest większa lub równa podwójnej liczbie górniczej zębów.
![]()
W korekcji tej stosuje się odsunięcie narzędzia dla mniejszego koła, aby uniknąć podcinania. Do dużego koła dosuwa się narzędzie o taką samą wartość. Odległość między osiami nie zmienia się. Zwiększa się grubość zęba u podstawy. Dzięki zwiększeniu ewolwentowego zarysu zęba maleje poślizg, rośnie cichobieżność i zwiększa się sprawność oraz wydłuża się żywotność.
2) Jakie są cech charakterystyczne korekcji P i kiedy ją można stosować?
Korekcje P można stosować gdy nie jest spełniony warunek:
![]()
lub w przypadku kiedy względy konstrukcyjne wymagają przesunięcia osi.
W korekcji tej następuje zmiana odległości osi.
3) W jaki sposób określa się graniczne współczynniki korekcji?
Graniczne górne wartości ![]()
określamy na podstawie liczby zębów z wykresu na krzywej O, natomiast wartość dolną ![]()
na krzywej P. Współczynnik x musi się zawierać pomiędzy krzywymi O i P.
4) Jak wpływa korekcja na geometrię zazębienia?
Korekcja powoduje:
-zwiększenie/zmniejszenie się wielkość promienia wierzchołków i stóp koła małego/koła dużego.
-zwiększenie/zmniejszenie się grubości zęba koła małego/dużego mierzona na okręgu podziałowym.
-zwiększenie stopnia pokrycia.
-występowanie korzystniejszego poślizgu.
-zwiększenie grubości zębów u podstawy.
5) Jak wpływa korekcja na wytrzymałość zębów?
Korekcja powoduje:
- zwiększenie wytrzymałości zęba na zginanie,
- zmniejszenie tarcia na skutek zmniejszenia poślizgu,
- zmniejszenie naprężeń stykowych w wyniku zmniejszenia krzywizny ewolwenty.
część 2:
Badanie sprawności przekładni zębatej.
Cel ćwiczenia:
Wyznaczenie sprawności przekładni pracującej jako reduktor i multiplikator.
Opis stanowiska:
K1,K2 - koła linowe o średnicy 185mm z nawiniętymi linami L1,L2
G1,G2 - odpowiednie obciążenia
i=10 - przełożenie reduktora
n1=1500obr/min - obroty normalne reduktora
N=9kW - moc przełożenia
Pomiary i obliczenia:
a) Badanie sprawności przekładni jako reduktora:
Początkowe położenie ciężaru D2 znajdowało się na podłodze, a szalka w górnym na wysokości ok. 60 cm(wysokość jest nieistotna). Następnie na szalkę nakładaliśmy odważniki, które powodowały jej jednostajny ruch w dół. W tej sytuacji przekładnia pracuje jako reduktor i jej sprawność liczymy ze wzoru poniżej:
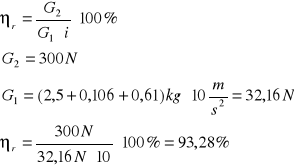
b) badanie sprawności przekładni jako multiplikatora:
W początkowym położeniu ciężar G2 znajdował się na pewnej wysokości nad podłogą, a szalka z obciążnikami (tak dobranymi by układ pozostawał w spoczynku) na podłodze. Następnie z szalki odejmowano odważniki do takiego momentu by ciężar G2 zaczął opadać w dół ruchem jednostajnym podnosząc równocześnie szalkę wraz z odważnikami. Sprawność dla przekładni pracującej, jako multiplikator oblicza się ze wzoru:
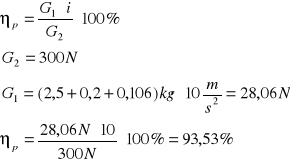
Wnioski:
Sprawności przekładni zębatej walcowej pracująca jako multiplikator i reduktor różnią się. Na uzyskane wartości sprawności wpływa kilka czynników:
Zużycie zębów i oddziaływanie między nimi, zużycie łożysk i straty związane z tarciem w łożyskach.
Odpowiedzi na pytania:
1) Na sprawność ogólną wpływają takie czynniki jak:
- przełożenie
- tarcie na powierzchni zębów
- opory ruchu w łożyskach
2) Prędkość ruchu kół zębatych znacznie obniża sprawność przekładni, ponieważ wraz ze wzrostem sprawności tarcie oraz inne opory ruchu również rosną.
3) Błędy montażu wpływają na zmianę sił w zazębieniu oraz powodują powstawanie dodatkowych obciążeń. Co za tym idzie, zmniejsza się wytrzymałość zębów oraz wzrasta ich zużycie. Błędy montażu mogą doprowadzić również do odkształcenia zazębienia, co wpływa na zmniejszenie sprawności przekładni a co za tym idzie skrócenie jej żywotności.
4) Na opory własne składają się takie czynniki jak:
- dokładność montażu
- metoda i jakość smarowania kół zębatych
- stan powierzchni współpracujących elementów
- opory powstające w łożyskach kół zębatych
- straty ciepła (wzrost temperatury współpracujących elementów)
5) Zapis sprawności reduktora
![]()
można zapisać w odniesieniu do klasycznego wzoru ![]()
stosując kolejno przekształcenia: ![]()
gdzie:
Ln - praca uzyskana
Lw - praca włożon
i=10 - przełożenie całkowite
n1=1500obr/min - obroty znamionowe
N=9kW - moc znamionowa
Wyszukiwarka
Podobne podstrony:
Sprzeglo klowe moje, Studia, IMIR- MIBM, III rok, PKM 2
przekładnia zębata W. Darowski(1), Studia, IMIR- MIBM, III rok, PKM 2
własnosci dynamiczne przetwornikow I rzedu - przykladowe, Studia, IMIR- MIBM, III rok, metro II, prz
ci ga 1, AGH - IMIR - IMIM, II ROK, PKM, PKM - egzamin II rok
Terytorium, studia, Administracja I stopnia, II rok Administracji, Prawo międzynarodowe
Wychowanie zdrowotne, Studia-PEDAGOGIKA, PEDAGOGIKA II ROK (resocjalizacyjna), teoria wychowania
Wychowanie zdrowotne, Studia-PEDAGOGIKA, PEDAGOGIKA II ROK (resocjalizacyjna), teoria wychowania
WYCHOWANIE PATRIOTYCZNE, Studia-PEDAGOGIKA, PEDAGOGIKA II ROK (resocjalizacyjna), teoria wychowania
Promocja zdrowia wieku starczego - treść, studia, Zdrowie Publiczne, II rok, Promocja zdrowia
InstrukcjaChZT, Studia, Przyszle lata, II rok pg, chemia
SPOSOBY BADANIA ZESPOŁU KLASOWEGO, Studia-PEDAGOGIKA, PEDAGOGIKA II ROK (resocjalizacyjna), pedagogi
Praca z tekstem(1), Studia-PEDAGOGIKA, PEDAGOGIKA II ROK (resocjalizacyjna), polski
PRAWO KARNE OPRACOWANA KSIĄŻKA, studia, Administracja I stopnia, II rok Administracji, Prawo karne
Podmioty prawa międzynarodowego, studia, Administracja I stopnia, II rok Administracji, Prawo między
WYKAZ STOWARZYSZEŃ POMOCY OSOBOM Z CHOROBĄ ALZHEIMERA, studia, Zdrowie Publiczne, II rok, Promocja z
technika wzmacniania pozytywnego i negatywnego, Studia-PEDAGOGIKA, PEDAGOGIKA II ROK (resocjalizacyj
więcej podobnych podstron