WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI METODĄ STOKESA
1.Cel ćwiczenia:
wyznaczenie współczynnika lepkości dla dwóch wybranych kulek;
zapoznanie się z wiskozymetrem Hopplera i wyznaczenie współczynnika lepkości cieczy zawartej w aparacie;
obserwacja ruchu ciał spadających w ośrodku ciekłym;
2. Podstawy teoretyczne:
Lepkość ( tarcie wewnętrzne ) jest zjawiskiem występowania sił stycznych przeciwdziałających wzajemnemu przemieszczaniu się elementów ciała sąsiadujących ze sobą Wskutek tarcia występującego między elementami ośrodka, poruszająca się cząstka " pociąga " ze sobą inną cząstkę wpływając na jej prędkość zależnie od wartości współczynnika lepkości danego gazu lub cieczy ( im większa lepkość tym prędkości sąsiadujących cząstek są bardziej zbliżone ).
Wszystkie rzeczywiste gazy i ciecze są lepkie, dlatego zjawisko lepkości jest bardzo ważne, jeżeli bierzemy pod uwagę przepływ cieczy lub ruch ciał spadających w ośrodku ciekłym.
Dla cieczy przepływającej stacjonarnie w rurze charakterystyczne jest jej rozwarstwienie, ze względu na prędkości poszczególnych warstw. Niejednorodność pola prędkości klasyfikuje lepkość do zjawisk transportu, gdzie następuje wymiana pędów cząstek prowadząca do ustalenia stałej prędkości w całym przekroju.
Dla małych prędkości przepływu mamy do czynienia z przepływem laminarnym, w który poszczególne warstwy cieczy oddziaływują między sobą. Siłę wzajemnego oddziaływania podał empirycznie Newton:
F = η S ( ![]()
)
η - współczynnik lepkości;
S - powierzchnia styku warstw;
dV/dx - gradient prędkości;
Wartość współczynnika lepkości zależy od temperatury ośrodka:
- dla cieczy: η = A * ![]()
; A ,B - stałe charakteryzujące ciecz;
- dla gazów: η = ![]()
;
λ - średnia droga swobodna cząstek gazu;
u - prędkość średnia cząsteczek;
ρ - gęstość gazu
Innym zagadnieniem związanym z lepkością jest swobodne spadanie ciał w ośrodku ciekłym. Siła oporu ( tarcia wewnętrznego ) charakterystyczna dla wszystkich cieczy rzeczywistych ma postać:
R = K l η v; K - stała zależna od kształtu ciała ( osiowo symetrycznego );
l - wymiar liniowy ciała;
v - prędkość opadania ciała;
Dla kuli K = 6π , l = r, a więc równanie przyjmuje postać: R = 6π r η v.
Wypadkowa siła działająca na kulkę ma postać:
F = P + W + R; P - siła ciężkości: P = ρKmg;
W - siła wyporu: W = ρwmg;
R - siła oporu: R = 6π r η v.
Z tego otrzymujemy równanie różniczkowe:
![]()
= A - Bv; A, B - stałe charakteryzujące ciecz określone wzorami:
A = ![]()
B = ![]()
Rozwiązaniem tego równania jest funkcja prędkości:
v = ![]()
(1 - e -B t ).
Okazuje się, że po pewnym czasie t →∞, kulka porusza się ruchem jednostajnym, co wynika ze stałego wzrostu siły oporu wraz ze wzrostem prędkości. Dlatego ciało spadające w ośrodku ciągłym może osiągnąć pewną prędkość graniczną wyrażoną równaniem:
vgr = ![]()
, co po podstawieniu za A i B daje ostatecznie wyrażenie na lepkość:
η = ![]()
Dla kulki spadającej w określonych warunkach ( co gwarantuje wiskozymetr Hopplera ) wyrażenie na współczynnik lepkości przyjmuje postać
η = K (ρk - ρw) * t; K - stała określająca warunki doświadczenia
t - czas spadania ciała;
3. Przebieg doświadczenia:
3.1. Wymiarowanie kulek:
3.1.1. Średnica:
ŚREDNICA |
d [mm] |
|||||||||
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
szklana |
6.08 |
6.085 |
6.075 |
6.075 |
6.075 |
6.08 |
6.07 |
6.085 |
6.075 |
6.075 |
ceramiczna |
6.5 |
6.6 |
6.77 |
7.085 |
6.63 |
6.675 |
6.81 |
6.51 |
6.66 |
6.85 |
dS = 6.0775;
dC = 6.709;
Tabela błędów pomiaru średnicy:
BŁĘDY |
Δd [mm] * 10 -3 |
|
|
|
|
|
|
|
|
|
|||||||||
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||||||||
szklana |
-2.5 |
7.5 |
2.5 |
2.5 |
2.5 |
-2.5 |
-7.5 |
7.5 |
2.5 |
2.5 |
|||||||||
ceramiczna |
209 |
109 |
-61 |
-376 |
79 |
34 |
-101 |
199 |
49 |
-141 |
|||||||||
Średni błąd kwadratowy pomiaru średnicy kulek:
σdS = 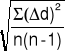
= ![]()
= 1.54 * 10 -3 mm;
σdC = 55.8 * 10 -3 mm;
3.1.2 Masy kulek:
MS = 0,4116 g;
MC = 0,4006 g;
ΔM = 0.0002 g - dokładność wagi laboratoryjnej.
3.1.3.Gęstość kulek:
rS = 0.303 cm rC = 0.335 cm
VS = 0.1175 cm3 VC = 0.158 cm3
ΔVS = 4.5 * 10 -13 cm3 ΔVC = 2.17 * 10 -8 cm3
ρS = ![]()
= ![]()
= 3.532 g cm -3 ρC = 2.543 g cm-3
Logarytmiczny błąd pomiaru gęstości: Δρ = (![]()
+ ![]()
) * ρ
ΔρS = 1.7 * 10-3 ΔρC = 4.99 * 10-4
3.2. Pomiary czasów swobodnego spadku kulek w ośrodku ciekłym:
3.2.1. Tabela wyników:
CZAS |
t [s] |
|
|
|
|
|
|
|
|
|
|||||||||
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||||||||
szklana |
2.7 |
2.8 |
2.8 |
2.8 |
2.7 |
2.8 |
2.8 |
2.8 |
2.8 |
2.8 |
|||||||||
ceramiczna |
4.2 |
4.1 |
4.2 |
4.2 |
4.1 |
4.3 |
4.1 |
4.2 |
4.2 |
4.2 |
|||||||||
tS = 2.78 s
tC = 4.18 s
3.2.2. Tabela błędów pomiaru czasu
BŁĘDY |
Δt [s] |
|
|
|
|
|
|
|
|
|
|||||||||
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||||||||
szklana |
0.08 |
-0.02 |
-0.02 |
-0.02 |
0.08 |
-0.02 |
-0.02 |
-0.02 |
-0.02 |
-0.02 |
|||||||||
ceramiczna |
-0.02 |
0.08 |
-0.02 |
-0.02 |
0.08 |
-0.12 |
0.08 |
-0.02 |
-0.02 |
-0.02 |
|||||||||
Średni błąd kwadratowy pomiaru czasu:
σtS = 0.013 s
σtC = 0.02 s
3.3 Obliczanie współczynnika lepkości
3.3.1.Wartość współczynnika lepkości:
η = ![]()
- ![]()
;
m - masa kulki;
t - czas swobodnego opadania;
h - droga swobodnego spadania;
r - promień kulki;
ρ - gęstość cieczy = 1240 kg m3
η1 = ![]()
- ![]()
= 0.459![]()
η2 = 0.505![]()
ηSR = 0.482![]()
3.3.2. Błąd pomiaru współczynnika lepkości:
dη=(![]()
- ![]()
+![]()
Wzór na Δη otrzymujemy poprzez podstawienie za różniczki obliczonych wartości błędów dla poszczególnych pomiarów. Z tego podstawienia otrzymujemy:
Δη = 0.0227
δη = (Δη/n) * 100% = 4.7 %
3.4. Badanie współczynnika lepkości cieczy zawartej w wiskozymetrze Hopplera :
3.4.1 Warunki doświadczenia:
K = 0.7941 * 10 -3 ![]()
cm3 g-1 s-1
ρK = (2.41 ± 0.01) g cm-3
ρC = (1.235 ± 0.005) g cm-3
3.4.2. Wyniki pomiaru czasu:
|
t [s] |
|
|
|
|
|
|
|
|
|
|||||||||
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||||||||
CZAS |
223.6 |
214.6 |
213.6 |
210.6 |
208.2 |
205.8 |
203.4 |
202.0 |
200.0 |
198.8 |
|||||||||
tW = 208.06 s
3.4.3. Błędy pomiaru czasu:
|
Δt [s] |
|
|
|
|
|
|
|
|
|
|||||||||
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||||||||
BŁĘDY |
-15.54 |
-6.54 |
-5.54 |
-2.54 |
-0.14 |
2.26 |
4.66 |
6.06 |
8.06 |
9.26 |
|||||||||
Średni błąd kwadratowy:
σtW = 2.44 s
3.4.4. Obliczanie współczynnika lepkości:
η = K t (ρK - ρC) = 0.7941 * 10-3 * 208.06 * ( 2.41 - 1.235) = 0.194![]()
3.4.5. Błąd pomiaru:
równanie różniczkowe do którego podstawiamy wyliczone wartości błędów;
d η = K (ρK - ρC) dt + K t dρK - K t dρC = 4.75 * 10 -3 = Δη
δη = (Δη/η) ∗ 100 % = 2.45 %
4. Wnioski:
Celem nasze doświadczenia było wyznaczenie współczynnika lepkości cieczy zawartej w wiskozymetrze Hopplera i naczyniu cylindrycznym. Podstawą teoretyczną do przeprowadzenia ćwiczenia było prawo Stokesa, które wykorzystywaliśmy przy obliczaniu prędkości i czasu spodania kulek w ośrodku ciągłym.
W pierwszej części ćwiczenia wrzucaliśmy do naczynia cylindrycznego wypełnionego cieczą dwie kulki i na podstawie ich rozmiarów, oraz czasu przebycia określonej drogi wyznaczaliśmy współczynnik lepkości danej cieczy. Metoda ta obarczona jest jednak wieloma błędami wynikającymi z niedokładności pomiaru czasu spadku, masy i średnicy kulek, które były w dużym stopniu ( relatywnie do rozmiarów ) zdeformowane. Ponadto do obliczeń teoretycznych wykorzystaliśmy wzór idealny, nie dokońca słuszny dla naczyń ograniczonych ( szczególnie, gdy kulka opada w pobliżu ściany naczynia ) Z tego wynika właśnie rozbieżność czasów spadania kulki, gdyż jej prędkość zależy od odległości od ścianki naczynia ( im bliżej scianki tym prędkość spadku jest mniejsza ). Niedokładność wyników dla obu kulek może wynikać z faktu, że są one zbudowane z różnych materiałów, o różnych współczynnikacz tarcia względem cieczy.
W drugiej części pomiarów badaliśmy ruch kulki w wiskozymetrze Hopplera. Dla dziesięciu pomiarów kolejne czasy swobodnego spadku kulki stale malały, co jest efektem wzrostu temperatury cieczy zawartej w wiskozymetrze pod wpływem tarcia kulki. Powoduje to obniżenie wartości współczynnika lepkości badanej cieczy . Mimo to otrzymane wyniki okazały się dokładniejsze, a obsługa wiskozymetru dużo łatwiejsza. Takze obliczenia przy ustalonych warunkach doświadczenia były mniej skomplikowane.
Wyszukiwarka
Podobne podstrony:
WYZNACZANIE MOMENTU BEZWŁADNOŚCI I SPRAWDZANIE TWIERDZENIA STEINERA 12, Nauka, MECHANIKA I WYTRZYMAŁ
WYZNACZANIE MOMENTU BEZWŁADNOŚCI I SPRAWDZANIE TWIERDZENIA STEINERA 9, Nauka, MECHANIKA I WYTRZYMAŁO
WYZNACZANIE MOMENTU BEZWŁADNOŚCI I SPRAWDZANIE TWIERDZENIA STEINERA 10, Nauka, MECHANIKA I WYTRZYMAŁ
Mechanika i Wytrzymałość Materiałów zestaw2
Mechanika i Wytrzymałość Materiałów W 1
POMIAR TWARDOŚCI SPOSOBEM BRINELLA, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzy
Mechanika - 3cie kolokwium, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość m
MECHANIKA KOLOS, Elektrotechnika PŁ, Mechanika i wytrzymałość materiałów
mechanika - teoria, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość materiałó
Mechanika i Wytrzymałość Materiałów W 4
6.Tensometria(3), POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość materiałów,
Mechanika i Wytrzymałość Materiałów zestaw3
Mechanika i Wytrzymałość Materiałów W 5
mechanika o wytrzymalosc materialow
Zagadnienia- mechanika, Politechnika Wrocławska Energetyka, 3 semestr, Mechanika i wytrzymałość mate
Wykłady i ćwiczenia mechanika, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałoś
więcej podobnych podstron