WYKŁAD 10

PRZEKSZTAŁCENIE LINIOWE

WARTOŚCI I WEKTORY WŁASNE ENDOMORFIZMU

Przykład

Rozpatrzmy przekształcenie płaszczyzny będące jednokładnością, która przekształca kwadrat jednostkowy na kwadrat o bokach [0, 3] i [0, 3]. Przekształcenie to mnoży współrzędne dowolnego wektora
= [x₁, x₂], przez liczbę 3 .

Oznaczając jednokładność przez f otrzymujemy ogólny wzór określający to przekształcenie:

f([x₁, x₂]) = [3 x₁, 3x₂]

Zauważmy, że jeśli
=[x₁, x₂],
=[y₁, y₂] i λ₁, λ₂ są dowolnymi stałymi rzeczywistymi to:

f([ λ₁x₁ + λ₂ y₁, λ₁x₂ + λ₂ y₂]) =

= [ 3(λ₁x₁ + λ₂ y₁), 3(λ₁x₂ + λ₂ y₂)] =

= [3 λ₁x₁, 3λ₁x₂] + [ 3λ₂ y₁, 3λ₂ y₂] =

= λ₁ f([x₁, x₂]) + λ₂ f([y₁, y₂]) =

Zdefiniowane przekształcenie ma zatem własność:

Podobnie można sprawdzić, że własność ta zachodzi dla

dowolnych

Definicja

Przekształcenie f : U → V , gdzie U i V są przestrzeniami liniowymi nazywamy przekształceniem liniowym jeżeli spełniona jest powyższa równość dla dowolnych liczb

oraz dla dowolnych wektorów

Przekształceniami liniowymi na płaszczyźnie są:

• Jednokładność względem punktu (0,0)

• Obroty względem punktu (0,0)

• Symetria względem punktu (0 ,0)

• Symetria względem prostej przechodzącej przez punkt (0,0)

• Rzuty na prostą przechodzącą przez punkt (0,0).

Wniosek

Dla dowolnego przekształcenia liniowego zachodzi:

(1)
tzn. wektor zerowy przestrzeni U

przekształca się na wektor zerowy przestrzeni V,

(2)

Dla przekształcenia liniowego f wprowadzamy pojęcie

jądra Ker(f) oraz obrazu przekształcenia Im(f) :

Okazuje się że:

Ker(f) jest podprzestrzenią wektorową U

Im(f) jest podprzestrzenią wektorową V

Związek miedzy wymiarami tych podrzestrzeni wektorowych

jest następujący:

dim(U) = dim(Ker(f)) + dim(Im(f))

Dowód podano w dalszej części wykładu.

Możemy też zdefiniować działania na przekształceniach

liniowych :

• dodawanie,

• odejmowanie,

• mnożenie przez liczbę

• składanie

• odwracanie,

podobnie jak robiliśmy to dla funkcji jednej zmiennej.

Działania na przekształceniach liniowych definują nowe przeksztalcenia liniowe.

Definicja

Jeśli f₁, f₂ : U → V są przekształceniami liniowymi,

to ich suma jest zdefiniowana następująco:

Definicja

Jeśli f : U → V jest przekształceniem liniowym, a λ

liczbą rzeczywistą to iloczyn przekształcenia przez liczbę

jest zdefiniowane następująco:

Definicja

Jeśli f₁ : U → V i f₂ : V →W są przekształceniami liniowymi, to ich złożenie jest zdefiniowane jako:

Definicja

Jeśli f : U → V jest przekształceniem liniowym, to przekształceniem odwrotnym nazywamy przekształcenie

mające własność

Warunkiem istnienia przekształcenia odwrotnego jest

• różnowartościowość przekształcenia f ( Ker(f)={0} )

• odwzorowywanie U na V ( dim Im(f)=dim (V) )

Postać macierzowa przekształcenia liniowego f: U → V

Zauważmy, że w omówionym przykładzie obraz f([x₁, x₂]) dowolnego wektora [x₁, x₂] można zapisać w postaci macierzowej jako:

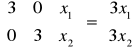
Przedstawimy teraz ogólną metodę znajdowania obrazu wektorów w przekształceniu liniowym. W pierwszym kroku określamy w jaki sposób transformują się wektory bazowe. Będzie to podstawa to określenia przekształceń dowolnego wektora z danej przestrzeni.

Niech baza B przestrzeni liniowej U składa się z wektorów:

Określamy przekształcenia wektorów bazowych jako:

Dowolny wektor
wyrażamy za pomocą wektorów bazowych.

.

Co możemy krótko zapisać

Niech V będzie przestrzenią m - wymiarową z bazą
i oznaczymy przez w_ij j- tą współrzędną wektora
, gdzie j∈[1, m].

Wówczas:

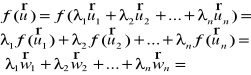
Ostatnie wyrażenie można zapisać jako

gdzie
oznacza macierz złożoną

z wektorów kolumnowych

a
jest wektorem kolumnowym.

Definicja

Macierz A_f postaci A_f =
nazywamy

macierzą przekształcenia f.

Konstrukcja macierzy przekształcenia liniowego f:

Krok-1. Znaleźć obrazy wektorów

Krok-3 Znaleźć współrzędne wektorów

w bazie przestrzeni V :

Krok 2. Utworzyć macierz
przez wpisanie jako jej kolejnych

kolumn współrzędnych wektorów
tj.

Wtedy dla wektora oraz wektora

zachodzi związek

Przekształcenie liniowe jest jednoznacznie wyznaczone przez podanie macierzy przekształcenia liniowego dla ustalonych baz przestrzeni U i V. Okazuje się poza tym, że własności przekształceń liniowych można interpretować w terminach macierzy tego przekształcenia.

Jeżeli w przestrzeni U następuje zmiana bazy

opisana przez macierz P a w przestrzeni V następuje zmiana bazy
opisana przez macierz Q to macierz przekształcenia liniowego w nowych bazach ma postać:

Przykład - macierz obrotu

Przekształcenie, w którym znajdujemy obraz punktu powstały w wyniku jego obrotu o kąt α, jest opisane wzorem:

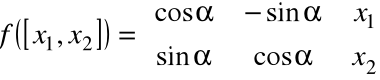
Zatem, macierz obrotu o kąt α ma postać:

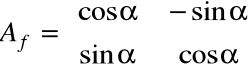
Zauważmy, że det A_f =1, zatem rząd A_f = 2. Wynika to z tego, że obrazem przestrzeni R² jest przy obrocie jest cała przestrzeń R².

Uwaga

Jeżeli f jest przekształceniem liniowym określonym na wektorach w
o wartościach będących wektorami z
, to macierz
jest wymiaru m x n.

Przykład

Niech f₁ będzie jednokładnością postaci f₁([ x₁, x₂]) = [ 3x₁, 4x₂], a f₂ obrotem o kąt α na płaszczyźnie.

Czemu odpowiada złożenie przekształceń f₁° f₂ ?

Okazuje się, że macierz A_{f2° f1} jest iloczynem macierzy A_f2 i A_f1 zatem:

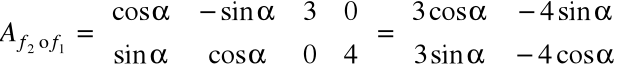
Podstawowe własności macierzy przekształcenia liniowego

Niech: rząd A_f = r

Wiemy, że metoda eliminacji pozwala na doprowadzenie macierzy A_f do postaci:

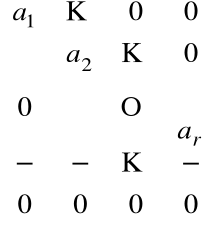
Elementarne operacje wierszowe nie zmieniają wartości wyznaczników, więc zachowują liniową niezależność wektorów

Obliczamy wartość:

gdzie jako wektor
przyjmujemy kolejno:

Stąd

,

................................

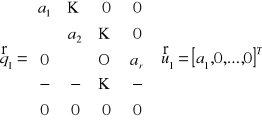
[ 0, 0, ..., 0] - (m - r) wierszy.

Każdy wektor
jest kombinacją liniową wektorów

Twierdzenie: rząd = dim Im(f)

Algorytm dla bazy w Im(f).

Krok 1. Wykonaj operacje wierszowe metody eliminacji na A_f.

Zapisz współczynniki główne a₁, a₂, ..., a_r.

Utwórz wektory

Krok 2. Utwórz macierz

Wykonaj w B operacje wierszowe odwrotne do operacji w Kroku 1. i w odwrotnej kolejności.

Zapisz otrzymaną macierz C.

Wynik: Kolumny macierzy C tworzą bazę w Im(f).

Twierdzenie

Jeśli dim U = n to wówczas :

dim Ker(f) = n - r = n - R( )

n = dim Im(f)+ dim Ker(f) = rząd + dim Ker(f)

dimU = dim Im(f)+ dim Ker(f)

Klasyfikacja przekształceń liniowych

Przekształcenie liniowe nazywamy homomorfizmem i oznaczamy przez Hom(U,V)

Przekształcenie liniowe nazywamy endomorfizmem i oznaczamy przez End(V)= Hom(V,V)

Przekształcenie liniowe które jest bijekcją nazywamy izomorfizmem i oznaczamy przez Izo(U,V)

Izomorfizm przekształcający nazywamy automorfizmem i oznaczamy przez Aut(V)=Izo(V,V)

Wartości własne i wektory własne endomorfizmu End(V)

Definicja

Endomorfizmem liniowym przestrzeni V nazywamy przekształcenie liniowe
.

Uwaga

Macierz endomorfizmu jest macierzą kwadratową.

Definicja

Niech V będzie przestrzenią liniową, wówczas:

Wektor
nazywamy wektorem własnym endomorfizmu L, jeśli istnieje λ ∈ R(C) takie, że

Liczbę λ nazywamy wartością własną endomorfizmu L.

• Wektor własny endomorfizmu (
  ) =

wektor własny macierzy przekształcenia.

• Wartość własna endomorfizmu (
  ) = wartość własna macierzy przekształcenia.

Przykład 1

Wówczas: f((1, 1, 1)) = (5, 5, 5) = 5(1, 1, 1)

Wartość własna: 5

Wektor własny: (1, 1, 1)

Przykład 2

Niech
będzie jednokładnością o skali λ, tzn.

Wówczas każdy wektor
jest wektorem własnym

tego przekształcenia o wartości własnej λ.

Przykład 3

Niech
będzie obrotem o kąt
, czyli

To przekształcenie nie ma żadnych wartości własnych,

tzn. żaden wektor nie przechodzi na swoją wielokrotność.

Przestrzeń wektorów własnych

1. Zbiór
przy ustalonym λ

jest podprzestrzenią liniową V

2.
jest podprzestrzenią niezmienniczą przekształcenia L

tzn.

3.

4.
(
- krotność wartości własnej λ)

5.

Baza wektorów własnych

1. jeżeli przekształcenie liniowe L ma n różnych wartości własnych to odpowiadające im wektory własne są liniowo niezależne oraz tworzą bazę przestrzeni V

2. jeżeli przekształcenie L ma r różnych wartości własnych

a wymiary odpowiadających im

przestrzeni wektorów własnych
spełniają związek:

to istnieje baza przestrzeni V złożona z wektorów

własnych przekształcenia liniowego L

3. jeżeli wektory własne

przekształcenia liniowego L tworzą bazę przestrzeni V to

macierz przekształcenia w tej bazie ma postać diagonalną

gdzie na przekątnej stoją wartości własne

Diagonalizowalność macierzy A(nxn) (rzeczywistej lub zespolonej)

Następujące warunki są równoważne:

• macierz A jest diagonalizowalna

• wektory własne A tworzą bazę przestrzeni
  

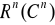
• postać diagonalna D macierzy A dana jest wzorem:

gdzie P jest macierza przejścia z bazy kanonicznej do bazy

wektorów własnych

(wektory własne są kolumnami macierzy P)

Uwaga: Dla rzeczywistej macierzy symetrycznej :

• wszystkie wartości własne są rzeczywiste

• wektory własne tworzą bazę

Znajdowanie wartości i wektorów własnych

Wartość
jest wartością własną przekształcenia liniowego L

macierzy A wtedy i tylko wtedy gdy zachodzi:

det(A-λI)=0

Wektor
jest wektorem własnym L

odpowiadającym wartości własnej
wttw gdy zachodzi:

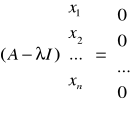
PROBLEM

Znaleźć niezerowy wektor
, którego obraz
jest jego

liniową wielokrotnością λ.

Mamy więc rozwiązać równanie macierzowe:

AX = λX

czyli:

lub

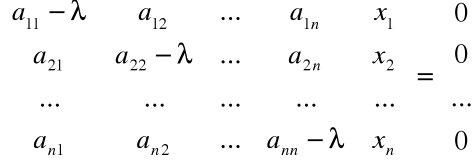
Niezerowe rozwiązanie równania
, istnieje wtedy i tylko wtedy, gdy macierz
jest nieosobliwa, czyli gdy jej wyznacznik jest równy 0.

Definicja

Równanie: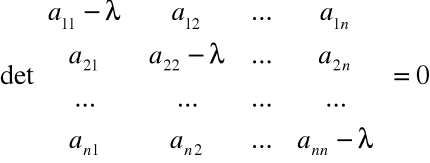

nazywamy równaniem charakterystycznym macierzy A, a wielomian det (A - λI) wielomianem charakterystycznym.

Twierdzenie

Pierwiastki równania charakterystycznego są wartościami własnymi macierzy A.

Przykład 1

Znaleźć wartości i wektory własne przekształcenia f o macierzy

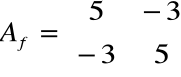
Z równania charakterystycznego :

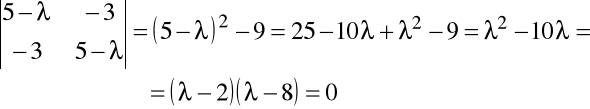
Wartości własne macierzy: λ₁=2, λ₂=8.

Znajdowanie wektorów własnych odpowiadających wartościom własnym:

• dla każdej wartości własnej rozwiązujemy równanie

Dla λ₁=2 otrzymujemy:

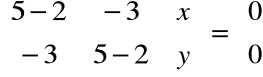
, czyli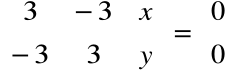

Rozwiązując układ równań: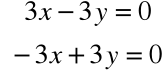

otrzymujemy na przykład wektor: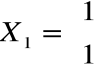

Wszystkie wektory postaci λX1 są wektorami własnymi. Wybieramy reprezentanta spośród wektorów własnych.

Dla λ₁=8 otrzymujemy układ:

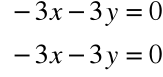
co daje np. wektor:

.

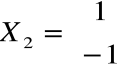
W powyższym przykładzie wektory własne stanowiły bazę przestrzeni V. Zachodzi to m.in. w przypadku gdy dim V=n a przekształcenie liniowe ma n różnych wartości własnych.

W przypadku gdy wektorów własnych liniowo niezależnych jest za mało to można je uzupełnić do pełnej bazy tzw. wektorami dołączonymi.

Procedura taka opisana jest w poniższych przykładach.

Rozpatrzmy teraz przykład przekształcenia dla którego wektory własne nie stanowią bazy w przestrzeni V.

Przykład 2

Znaleźć wartości i wektory własne przekształcenia f o macierzy

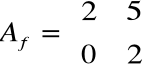
oraz bazę przestrzeni w oparciu o wektory własne.

Z równania charakterystycznego

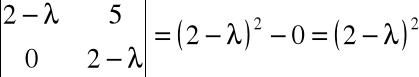
otrzymujemy jedną podwójną wartość własną tej macierzy:

λ₁=λ₂=2.

Znajdujemy wektory własne odpowiadające tej wartości własnej:

• Aby znaleźć pierwszy wektor własny rozwiązujemy równanie (A-λI)X1=0

Czyli dla λ₁ = λ₂ = 2:

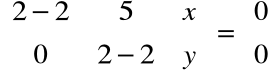
, stąd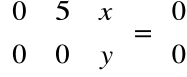

Rozwiązując układ równań: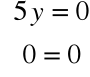

otrzymujemy np. wektor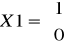
.

Pozostałe wektory własne będą liniowo zależne od tego wektora, zatem wektory własne nie będą stanowiły bazy.

W tym przypadku wektory własne można uzupełnić do bazy .

Ponieważ krotność wartości własnej równa jest 2

to drugi wektor bazy znajdujemy rozwiązując równanie:

(A-λI)X2=X1

Czyli musimy rozwiązać równanie:

,

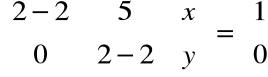
stąd: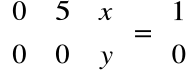

Rozwiązując układ równań: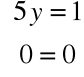

otrzymujemy na przykład wektor bazy nie będący wektorem własnym: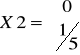
.

Teraz wektory X1 i X2 stanowią bazę przestrzeni V,

ale tylko X1 jest wektorem własnym.

W tej bazie macierz przekształcenia liniowego ma postać:

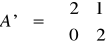
Przykład 3

Znaleźć wartości i wektory własne przekształcenia f o macierzy

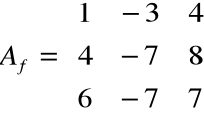
oraz bazę przestrzeni w oparciu o wektory własne.

Z równania charakterystycznego

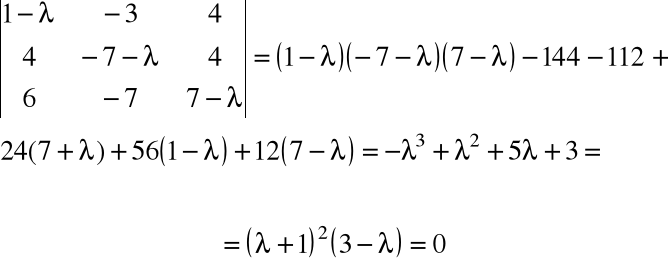
Wartość własna podwójna: λ₁=λ₂= -1 oraz pojedyncza: λ₃= 3

Znajdujemy wektory własne odpowiadające wartości własnej λ₁=λ₂= -1:

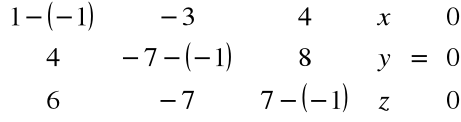
stąd: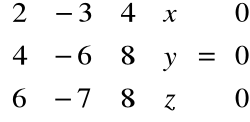

Po eliminacji: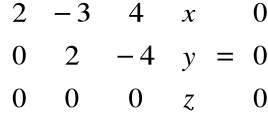

Rozwiązując układ równań:

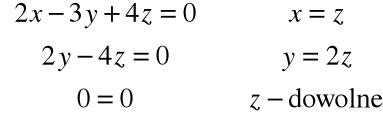
otrzymujemy wektor własny: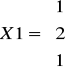

Pozostałe wektory własne są liniowo zależne od tego wektora.

Ponieważ krotność tej wartości własnej wynosi 2 to brakujący drugi wektor bazy uzupełniamy przez rozwiązanie równania:

(A-λI)X2=X1

Teraz zatem musimy rozwiązać równanie:

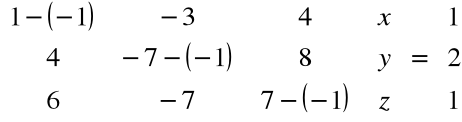
stąd: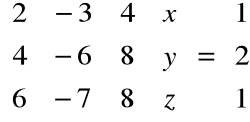

Po eliminacji: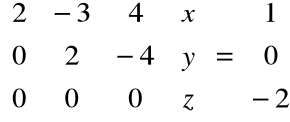

Rozwiązując układ równań: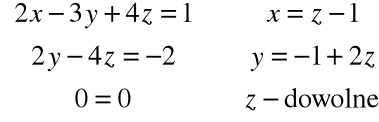

otrzymujemy drugi wektor bazy nie będący wektorem własnym:

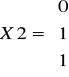
Pozostało jeszcze znaleźć wektory własne odpowiadające wartości własnej λ₃=3:

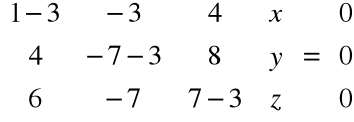
Stąd: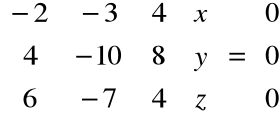

Po eliminacji: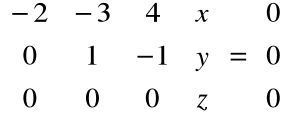

Rozwiązując układ równań: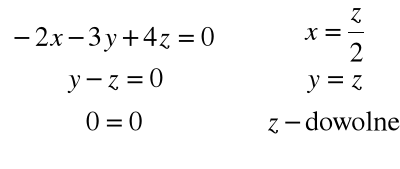

otrzymujemy wektor własny: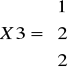

Pozostałe wektory własne dla tej wartości własnej bedą liniowo zależne od tego wektora.

Zatem wektory X1, X2, X3 stanowią bazę przestrzeni ale tylko dwa z nich a mianowicie X1 i X3 są wektorami własnymi przekształcenia.

Macierz przekształcenia w tej bazie ma postać:

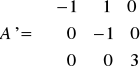
Przykład 4

Niech f: R² → R² będzie obrotem o kąt π/2, czyli przekształceniem liniowym o macierzy:

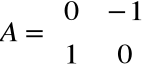
Z równania charakterystycznego:

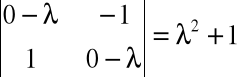
nie otrzymujemy pierwiastków rzeczywistych, a zatem:

obrót nie ma wektorów własnych na płaszczyźnie.

Twierdzenie

Niech f: V → V jest przekształceniem liniowym t.że dim V=n .

• Jeśli wartości własne f są różne, to odpowiadające im wektory własne są liniowo niezależne.

• Jeżeli różnych wartości własnych jest n

to wektory własne tworzą bazę przestrzeni V.

• Macierz przekształcenia f w bazie wektorów własnych

ma postać diagonalną:

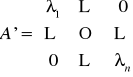
gdzie λ_i są wartościami własnymi.

Definicja

Macierze A i B wymiaru nxn są podobne gdy

A=P
BP

dla pewnej macierzy odwracalnej P.

Zadanie kontrolne:

Sprawdź czy macierz B=
jest diagonalizowalna.

Diagonalizowalność macierzy A oznacza zatem jej podobieństwo do macierzy diagonalnej. Z przykładu wynika,

że macierz nie jest diagonalizowalna jeśli jej wartości własnej o pewnej krotności k nie odpowiada k niezależnych wektorów własnych.

Okazuje się, że w sytuacji gdy macierz A nie jest podobna do macierzy diagonalnej, to jest podobna do macierzy bliskiej macierzy diagonalnej, tzw. macierzy blokowej Jordana.

Definicja

Macierz kwadratowa, górnotrójkątna A jest macierzą blokową Jordana, jeśli:

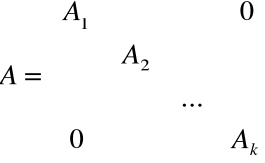
gdzie każda z macierzy A_k jest kwadratowa i ma postać:

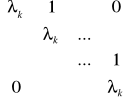
Macierze A_k nazywamy klatkami Jordana macierzy A.

Uwaga

Liczby λ_k występujące w macierzy Jordana są jej wartościami własnymi. Najmniejsza możliwa klatka Jordana jest macierzą 1x1, składającą się tylko z jednej wartości własnej.

Twierdzenie

Niech A będzie macierzą wymiaru nxn.

Wówczas A jest podobna do macierzy Jordana.

Twierdzenie

• Niech A będzie macierzą kwadratową.

• Niech B będzie macierzą blokową Jordana podobną do A.

• Niech λ∈K będzie wartością własną macierzy A.

• Niech a₀ = n, a_m=R[(A-λI)^m] dla m=1,2...n

Wówczas:

• (a_m-1 - a_m ) ≥ 0

• (a_m-1 - a_m) jest liczbą klatek Jordana

wymiaru większego bądź równego m w macierzy B,

zawierających wartość własną λ.

Znajdowanie macierzy Jordana dla macierzy A

Przykład 1

Znaleźć macierz Jordana dla macierzy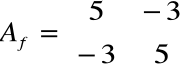
.

Ponieważ wartości własne były pojedyncze (λ₁=2, λ₂=8),

macierz Jordana możemy zapisać natychmiast:

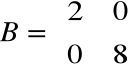
Przykład 2

Znaleźć macierz Jordana dla macierzy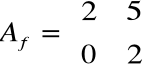
.

Wartość własna macierzy: λ₁=λ₂= 2.

Zatem obliczamy:

a₀ = 2 - wymiar macierzy,

a₁=1 - rząd macierzy
=
.

Stąd: a₀ - a₁ =1

Liczba klatek rozmiaru większego bądź równego 1 wynosi 1, czyli klatka musi mieć wymiar 2x2 i macierz Jordana jest postaci:

.

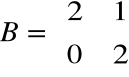
Przykład 3

Znaleźć macierz Jordana dla macierzy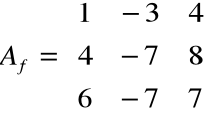
.

Wartość własna macierzy: λ₁=λ₂= -1

Zatem obliczamy:

a₀=3 - wymiar macierzy

a₁=2 - rząd macierzy
=

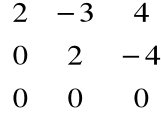
Stąd: a₀ - a₁ =1

Liczba klatek wymiaru większego bądź równego 1 odpowiadających wartości własnej -1 wynosi 1,

czyli musi to być klatka 2x2.

Zatem macierz Jordana jest postaci:

.

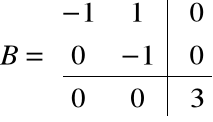
Algebra Liniowa z Geometrią

28

---