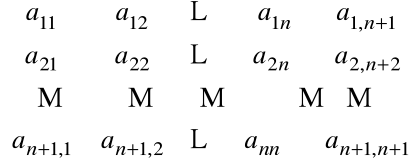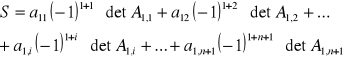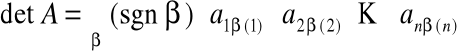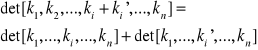WYKŁAD - 4

WYZNACZNIKI I ICH ZASTOSOWANIA

W wykładzie tym przedstawimy definicje i własności wyznacznika, który ma zastosowanie przy rozwiązywaniu układów algebraicznych równań liniowych, w geometrii i analizie.

• GENEZA WYZNACZNIKA

Rozpatrzmy układ równań liniowych z dwiema niewiadomymi

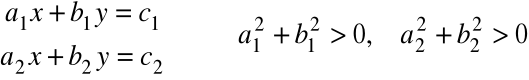
Rozwiązanie układu metodą przeciwnych współczynników

• Mnożymy pierwsze równanie przez
  

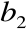
• Mnożymy drugie równanie przez
  

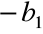
• Dodajemy równania stronami.

Stąd:

Podobnie:

Rozwiązanie układu równań jest postaci:

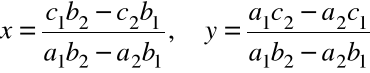
przy założeniu:

Macierz główna układu dwóch równań ma postać

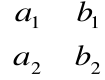
Definicja

Wyznacznikiem macierzy głównej układu dwóch równań nazywamy liczbę równą:

i oznaczamy przez: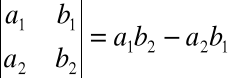

Zauważmy, że rozpatrując dodatkowe następujące dwa wyznaczniki

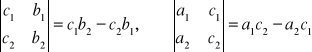
możemy rozwiązanie układu równań zapisać w postaci:

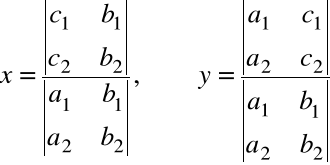
Jest to przypadek szczególny postaci rozwiązań układu n równań liniowych, który poznamy w wykładzie 5

Przykład

Obliczyć wyznacznik

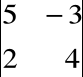
= 20 - (-6) = 26

Rozpatrzmy macierz kwadratową A wymiaru nxn

A =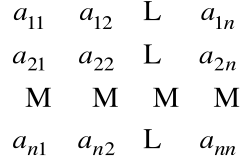

Dla takiej macierzy A zdefiniujemy liczbę nazywaną wyznacznikiem A i oznaczaną detA lub

Możemy zatem wyznacznik traktować jako funkcję, która każdej macierzy kwadratowej rzeczywistej (zespolonej) przypisuje liczbę rzeczywistą (zespoloną).

Indukcyjna definicja wyznacznika względem ilości wierszy n - rozwinięcie względem pierwszego wiersza

Niech A oznacza macierz kwadratową wymiaru n

Krok 1. Dla n=1, detA = a11

Krok 2. Założenie: mamy zdefiniowany wyznacznik wymiaru n Teza: Definiujemy wyznacznik wymiaru (n+1) (n+1) dla i = 1, 2, ..., n+1: Wykreślamy z macierzy A wiersz 1 i kolumnę i Dla pozostałej macierzy obliczamy det A Tworzymy sumę po wszystkich i Przyjmujemy det (A) = S

S jest sumą następujących iloczynów: każdy element a_1i pierwszego wiersza przemnażamy przez
i przez wyznacznik macierzy otrzymanej przez skreślenie pierwszego wiersz i i-tej kolumny. Otrzymane iloczyny dodajemy.

Wyznacznik liczbowej macierzy kwadratowej

oznaczamy również symbolem

Dla wyznacznika mówimy podobnie jak o macierzy o jego stopniu, wierszach i kolumnach.

Pamiętajmy, że wyznacznik jest określony

tylko dla macierzy kwadratowych

Przykład

Obliczyć z definicji wyznacznik macierzy

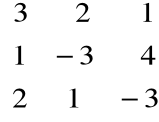
detA =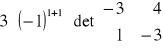
+

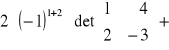
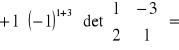
= 15 + 22 + 7 = 44

Zauważmy, że stosując definicję indukcyjną do macierzy kwadratowej A stopnia 2 otrzymamy wynik zgodny z pierwszą definicją przedstawioną na wykładzie.

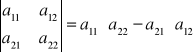
Definicja

Niech
będzie macierzą kwadratową stopnia n. Dopełnieniem algebraicznym elementu
nazywamy liczbę

gdzie
oznacza macierz stopnia n-1 otrzymaną przez skreślenie i-tego wiersza i j-tej kolumny macierzy.

Twierdzenie(Laplace'a o rozwinięciu wyznacznika)

Dla macierzy kwadratowej A stopnia n

Rozwinięcie względem i-tego wiersza

i = 1,2....n

Rozwinięcie względem j-tej kolumny

j = 1,2....n

Zatem wyznacznik jest równy sumie iloczynów elementów

i-tego wiersza i ich dopełnień algebraicznych

jak również sumie iloczynów elementów j-tej kolumny

i ich dopełnień algebraicznych.

Przedstawimy teraz kolejną metodę, którą w prosty sposób obliczymy wyznacznik macierzy stopnia 3.

Metoda Sarrusa

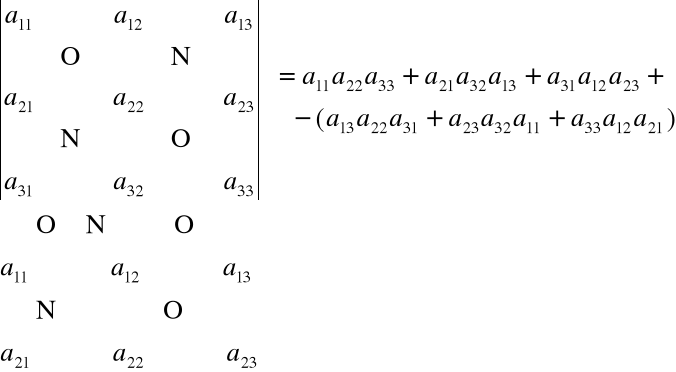
Pod wyznacznikiem dopisujemy dwa pierwsze wiersze.

Iloczyny wzdłuż głównej przekatnej sumujemy ze znakiem +

a iloczyny wzdłuż drugiej przekatnej sumujemy ze znakiem -

i otrzymujemy wartość wyznacznika.

Identyczny wynik uzyskamy jeżeli obok wyznacznika

dopiszemy dwie pierwsze kolumny.

Przykład

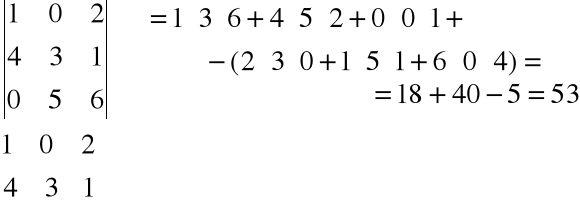
Wyznacznik można także zdefiniować używając pojęcia permutacji i jej znaku.

Permutacyjna definicja wyznacznika

Permutacja zbioru:
:

ciąg
elementów tego zbioru,

w którym każda liczba powtarza się tylko raz.

Para (p_i , p_j) tworzy inwersję, gdy p_i > p_j dla i < j.

Liczba permutacji zbioru n - elementowego: n!

Permutacja parzysta - parzysta ilość inwersji.

Permutacja nieparzysta - nieparzysta ilość inwersji

Znak permutacji -

Przykład

Rozpatrzmy permutację (2, 3, 4, 5, 1) zbioru

Liczba inwersji = 4 { (2,1),(3,1),(4,1),(5,1) }

permutacja parzysta
znak permutacji wynosi 1

Twierdzenie

Dla macierzy A = mamy , gdzie przebiega wszystkie permutacje zbioru {1, 2, ...,n}.

Obliczanie wyznacznika macierzy metodą permutacyjną (dla macierzy 3 x 3)

• Wypisujemy wszystkie permutacje zbioru {1, 2, 3}

• Tworzymy iloczyny współczynników macierzy

w następujący sposób

Permutacja wyjściowa	Permutacja obliczona	Znak permutacji	Iloczyn współczynników
1, 2, 3	1, 2, 3	1
	1, 3, 2	-1	a
	2, 1, 3	-1
	3, 2, 1	-1
	2, 3, 1	1
	3, 1, 2	1

• Dodajemy utworzone iloczyny, które przepisujemy

ze znakiem „+” dla permutacji parzystej,

ze znakiem „-” dla permutacji nieparzystej

det A =
- a
-
-
+

+
+

Tak więc otrzymujemy wspomniany poprzednio wzór Sarrusa

Przykład

Obliczyć wyznacznik macierzy metodą permutacyjną

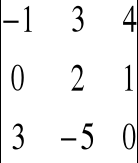
permutacja parzysta

permutacja nieparzysta

permutacja nieparzysta

permutacja nieparzysta

permutacja parzysta

permutacja parzysta

detA=

Metoda Sarrusa daje oczywiście ten sam wynik

Aksjomatyczna definicja wyznacznika

Wyznacznikiem macierzy kwadratowej nazywamy

funkcję rzeczywistą lub zespoloną majacą własności:

1
2
3
4

Gdzie
oznacza i-tą kolumnę danej macierzy

a
oznacza liczbę rzeczywistą lub zespoloną.

Twierdzenie - własności wyznaczników

Wyznacznik = 0

• Wyznacznik macierzy mającej wiersz (kolumnę) zerową jest równy 0 np.

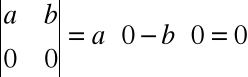
• Wyznacznik macierzy o dwóch jednakowych wierszach (kolumnach) jest równy 0 np.

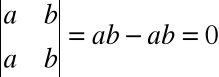
• Wyznacznik o dwóch proporcjonalnych wierszach (kolumnach) jest równy 0 np.

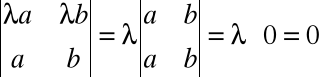
• Jeżeli w macierzy jeden z wierszy (lub jedna z kolumn) jest kombinacją liniową pozostałych wierszy (lub kolumn), to wyznacznik tej macierzy jest równy 0 np.

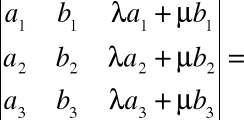
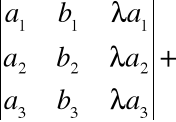
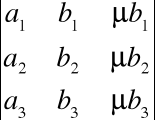
Wyznacznik nie zmieni się

• Wyznacznik macierzy nie zmieni wartości, jeżeli do wiersza (lub kolumny) macierzy dodamy kombinację liniową pozostałych wierszy (lub kolumn) np.

=

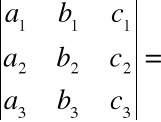
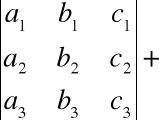
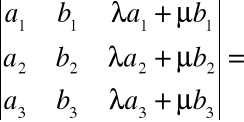
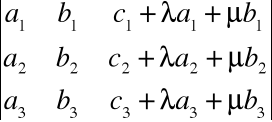
Własność ta może być wykorzystana w tzw.redukcji wierszowej lub kolumnowej

Wyznacznik zmieni się

• Przestawienie dwóch wierszy (kolumn) w macierzy jest równoważne pomnożeniu wyznacznika przez -1

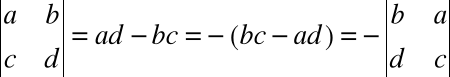
• Mnożąc wiersz (kolumnę) macierzy przez liczbę mnożymy wyznacznik tej macierzy przez tę liczbę np.

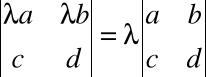
Wyznacznik macierzy specjalnej postaci

• Wyznacznik macierzy kwadratowej jest równy wyznacznikowi macierzy względem niej transponowanej

np.

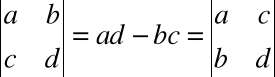
•Wyznacznik macierzy, której elementy pewnej kolumny (wiersza) są sumami dwóch składników jest równy sumie wyznaczników macierzy, w których elementy tej kolumny (wiersza) są zastąpione tymi składnikami np.

=

+

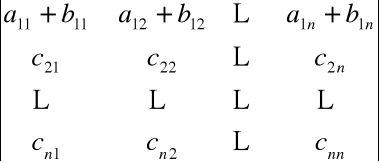
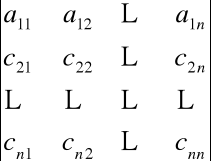
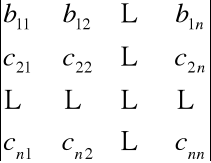
Algorytm Gaussa obliczania wyznaczników

W oparciu o powyższe twierdzenie łatwo uzasadnić prawdziwość następującego algorytmu Gaussa obliczania wyznaczników, który polega na sukcesywnym obniżaniu stopnia obliczanego wyznacznika

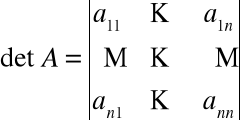
i
.

Wówczas

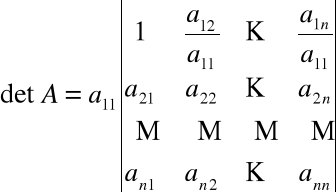
W ostatnim wyznaczniku od i-tego wiersza odejmujemy wiersz pierwszy przemnożony przez
.

W efekcie otrzymamy

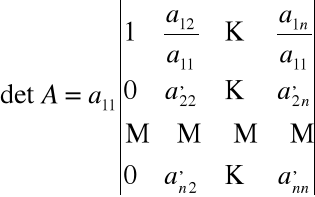
gdzie: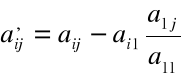

Transponując ostatni wyznacznik i korzystając z definicji indukcyjnej wyznacznika otrzymamy, że

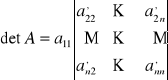
Gdzie wyznacznik po prawej stronie jest stopnia n-1.

Przykład

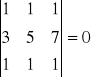
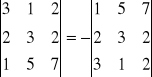
Stosując rozwinięcie indukcyjne i twierdzenie Laplace'a łatwo uzasadnić, że wyznacznik macierzy

dolno- lub górno-trójkątnej jest równy

iloczynowi elementów diagonalnych.

Twierdzenie (o wyznaczniku iloczynu macierzy)

Jeśli A i B są macierzami kwadratowymi tego samego stopnia, to zachodzi:

ODWRACANIE MACIERZY

Definicja

Macierzą odwrotną do macierzy kwadratowej A nazywamy macierz oznaczoną przez
, taką, że

Twierdzenie

• Macierz odwracalna A (tzn. taka, do której istnieje macierz odwrotna) jest macierzą nieosobliwą, to jest taką, że
  

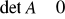
• Macierz odwrotna
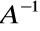
  do macierzy nieosobliwej A jest nieosobliwa.

• Wyznacznik macierzy odwrotnej
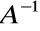
  jest równy odwrotności wyznacznika macierzy A.

Definicja

Macierzą dołączoną
macierzy kwadratowej A nazywamy macierz transponowaną macierzy utworzonej z dopełnień algebraicznych elementów macierzy A.

Twierdzenie: Macierz odwrotna dana jest wzorem

Własnosci operacji odwracania macierzy:

1
2
3
4
5
6

Algorytm obliczania macierzy odwrotnej do macierzy A

k1	Oblicz wyznacznik det (A)
k2	Jeżeli det(A) = 0 to koniec algorytmu Jeżeli det(A) ≠ 0 to przejdź do k3
k3	Oblicz macierz minorów
k4	Oblicz macierz dopełnień
k5	Transponuj macierz dopełnień
k6	Oblicz macierz odwrotną jako
k7	Sprawdź czy tak obliczona macierz spełnia warunki: Jeżeli NIE to wróć do kroku k1 Jeżeli TAK to koniec algorytmu

Przykład

Obliczyć macierz odwrotną do macierzy

A =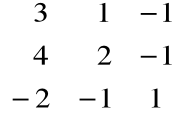

• Obliczamy wyznacznik macierzy

det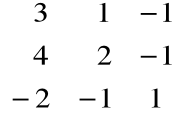
= 1

• Obliczmy dopełnienia algebraiczne elementów macierzy A

,
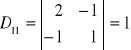
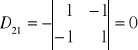
, itd.

• Tworzymy macierz dopełnień algebraicznych

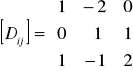
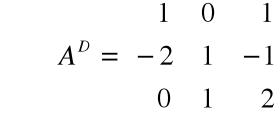
• Obliczamy
  
  =
  

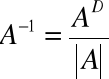
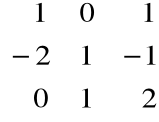
Algebra Liniowa z Geometrią

16