Zachodniopomorski Uniwersytet Technologiczny Instytut Automatyki Przemysłowej Zakład Metrologii
Sprawozdanie z wykonania ćwiczenia
Temat: Mostek niezrównoważony.
Skład zespołu 2: Krzysztof Łukasik Robert Głogowski Piotr Piskorz Mateusz Bondaronok	Prowadzący: dr inż. Andrzej Czajkowski	Data wykonania: 03-12-2008r.	Ocena:	Podpis:

1. Cel ćwiczenia

Celem ćwiczenia było zapoznanie się z metodą wyznaczania charakterystyk przetwarzania mostka niezrównoważonego oraz zbadanie możliwości zastosowania mostka niezrównoważonego jako miernika względnych odchyłek rezystancji - mostka procentowego. Zapoznaliśmy się z mostkiem odchyłowym i z procentowym, a następnie za ich pomocą dokonaliśmy obserwacji.

2. Spis aparatury

• Uniwersalny zasilacz stabilizowany UZS - 01

• Multimetr METEX MXD - 4660A

• Opornik stosunkowy typ SR - 28

• Opornik dekadowy MDR - 93 - 6AA

• Opornik dekadowy DR4B - 16

• Mostek procentowy MERATRONIK E - 308

3. Opis układu pomiarowego

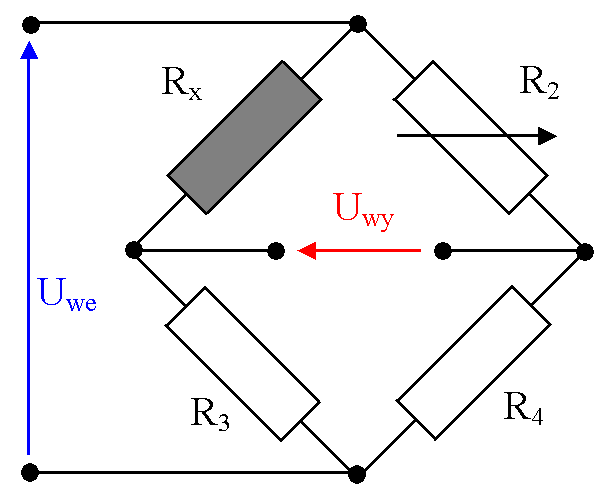
Mostki niezrównoważone są wykorzystywane głównie jako przetworniki zmiany rezystancji na napięcie wyjściowe. W ogólnym przypadku, napięcie wyjściowe mostka spełnia następujące równanie:

W mostku występują cztery gałęzie z rezystancjami R_n i przyrostami rezystancji ΔR_n. W stanie początkowym mostek jest zrównoważony (ΔR_n=0, U_wy=0). Działając na rezystancje R_n zmienia się jego rezystancję o ±ΔR_n. Zmiany rezystancji w gałęziach mostka powodują wystąpienie w przekątnej pomiarowej mostka sygnału niezrównoważenia w postaci prądu I_W lub napięcia U_W. Dla stałej wartości napięcia U_z zasilającego mostek, związek między zmianą rezystancji ΔR w gałęziach czujnikowych a napięciem wyjściowym U_W określają statyczne charakterystyki przetwarzania.

Ogólnie mostki niezrównoważone mają nieliniowe charakterystyki przetwarzania. Jedynie dla wybranych konfiguracji i przy ograniczeniach zakresów odstrojenia od stanu równowagi mogą być przyjęte liniowe charakterystyki przetwarzania. Odstępstwo od charakterystyki liniowej można ocenić za pomocą błędu liniowości:

3. Wyniki pomiarów

Pomiar 1: Pomiar odchyłów mostka

Y - sygnał wyjściowy (napięcie lub prąd) mostka

Y_n - znamionowy sygnał wyjściowy (napięcie 1V, prąd 10mA) mostka,

ε =
- względna zmiana rezystancji rezystora badanego,

ε_n - wartość znamionowa względnej zmiany rezystancji rezystora badanego (ε_n =1)

przy R₁ (ε=0) = 100,0Ω i R₂= R₃= R₄=100,0Ω

δ(
₎₌
-
-funkcja błędu nieliniowości

a) Przy zasilaniu napięciowym i wyjściu napięciowym (woltomierz) U-U

ε	Y [V]	Yn[V]		δ( )= -	δ( )[%]
0	0	0	0	0	0
0,1	0,1428	1	0,1428	0,0428	4,28
0,2	0,2726	1	0,2726	0,0726	7,26
0,3	0,3913	1	0,3913	0,0913	9,13
0,4	0,4999	1	0,4999	0,0999	9,99
0,5	0,5999	1	0,5999	0,0999	9,99
0,6	0,6923	1	0,6923	0,0923	9,23
0,7	0,7778	1	0,7778	0,0778	7,78
0,8	0,8572	1	0,8572	0,0572	5,72
0,9	0,9311	1	0,9311	0,0311	3,11
1,0	1,0000	1	1,0000	0,0000	0,00

b) Przy zasilaniu napięciowym i wyjściu prądowym (miliamperomierz) U-I

ε	Y[mA]	Yn[mA]		δ( )= -	δ( )[%]
0	0	0	0	0	0
0,1	1,613	10,000	0,1613	0,0613	6,13
0,2	3,017	10,000	0,3017	0,1017	10,17
0,3	4,257	10,000	0,4257	0,1257	12,57
0,4	5,356	10,000	0,5356	0,1356	13,56
0,5	6,338	10,000	0,6338	0,1338	13,38
0,6	7,220	10,000	0,7220	0,1220	12,20
0,7	8,021	10,000	0,8021	0,1021	10,21
0,8	8,745	10,000	0,8745	0,0745	7,45
0,9	9,405	10,000	0,9405	0,0405	4,05
1	10	10,000	1,0000	0,0000	0,00

c) Przy zasilaniu prądowym i wyjściu prądowym (miliamperomierz) I-I

ε	Y[mA]	Yn[mA]		δ( )= -	δ( )[%]
0	0	0	0	0	0
0,1	1,412	10,000	0,1412	0,0412	4,12
0,2	2,699	10,000	0,2699	0,0699	6,99
0,3	3,878	10,000	0,3878	0,0878	8,78
0,4	4,962	10,000	0,4962	0,0962	9,62
0,5	5,963	10,000	0,5963	0,0963	9,63
0,6	6,890	10,000	0,6890	0,0890	8,90
0,7	7,751	10,000	0,7751	0,0751	7,51
0,8	8,553	10,000	0,8553	0,0553	5,53
0,9	9,300	10,000	0,9300	0,0300	3,00
1,0	10,000	10,000	1,0000	0,0000	0,00

d) Przy zasilaniu prądowym i wyjściu napięciowym (woltomierz) I-U

ε	Y[V]	Yn[V]		δ( )= -	δ( )[%]
0	0	0	0	0	0
0,1	0,1223	1,000	0,1223	0,0223	2,23
0,2	0,2384	1,000	0,2384	0,0384	3,84
0,3	0,3492	1,000	0,3492	0,0492	4,92
0,4	0,4550	1,000	0,4550	0,0550	5,50
0,5	0,5559	1,000	0,5559	0,0559	5,59
0,6	0,6525	1,000	0,6525	0,0525	5,25
0,7	0,7450	1,000	0,7450	0,0450	4,50
0,8	0,8336	1,000	0,8336	0,0336	3,36
0,9	0,9186	1,000	0,9186	0,0186	1,86
1,0	1,0000	1,000	1,0000	0,0000	0,00

Wykresy pomiarów mostka odchyłowego:

Skąd wynikają różnice w wartościach błędów nieliniowości w przypadkach a, b, c i d. Który przypadek mostka jest najkorzystniejszy ze względu na najmniejszy błąd nieliniowości?

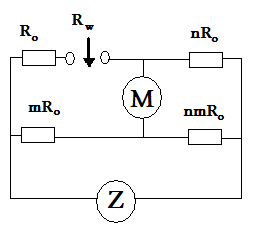
Otóż przyczyną tej różnicy jest parametr określający stopień nieliniowości charakterystyki mostka - β. Jest on równy odwrotności rezystancji R_ab widzianej z końcówek elementu R_w który jest dołączany do rezystora R_o pomnożonej przez R_o.

A więc:

Układy:	β dla m=1, n=1
U-U	½
U-I	¾
I-I	½
I-U	¼

Różnice w wartościach błędów nieliniowości w przypadkach a, b, c, d zależą od współczynnika β. Współczynnik ten, zgodnie z tabelką jest najmniejszy dla przypadku d - gdzie β równe jest ¼, zatem i wartość błędu nieliniowości dla tego przypadku jest najmniejsza, a więc jest to przypadek najkorzystniejszy.

Wyniki pomiaru pokrywają się z wynikami teoretycznymi. Na wykresie największe odchyły zaobserwowaliśmy podczas badania rezystorów w układzie wejście napięciowe - wyjście prądowe. Najmniejsze zaś odchylenia występowały w przypadku układu wejście prądowe, wyjście napięciowe. Układ o wejściu prądowym i wyjściu napięciowym jest najlepszym do porównywania dwóch wielkości jako najbardziej dokładnym.

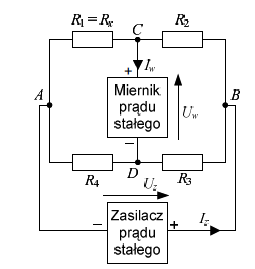
Pomiar 2: Pomiar odchyłów mostka dla m=100

Zwiększamy m-krotnie (m=100) wartość rezystancji rezystorów stosunkowych, tzn. R₃ = R₄ = mR₂ = 100. Układ zasilany jest prądowo, a wyjście jest napięciowe (oznaczenie - I-U).

ε	Y[V]	Yn[V]		δ( )= -	δ( )[%]
0	0	1,000	0,0000	0,0000	0,00
0,1	0,1006	1,000	0,1006	0,0006	0,06
0,2	0,2011	1,000	0,2011	0,0011	0,11
0,3	0,3015	1,000	0,3015	0,0015	0,15
0,4	0,4018	1,000	0,4018	0,0018	0,18
0,5	0,5018	1,000	0,5018	0,0018	0,18
0,6	0,6020	1,000	0,6020	0,0020	0,20
0,7	0,7017	1,000	0,7017	0,0017	0,17
0,8	0,8014	1,000	0,8014	0,0014	0,14
0,9	0,9007	1,000	0,9007	0,0007	0,07
1,0	1,0000	1,000	1,000	0,0000	0,00

Wykresy mostka odchyłowego dla m=100

Skąd pochodzi różnica między otrzymanymi wartościami błędów nieliniowości?

Szczególnym przypadkiem mostka niezrównoważonego jest mostek ze stosunkiem ramion. Zaletą tego układu jest możliwość wpływania na czułość i liniowość przetwarzania. Własność tą sprawdziliśmy właśnie w tym pomiarze.

Jak wcześniej wyjaśniłem nieliniowość zależy od parametru β. Gdy będziemy manipulować wartościami rezystorów, pamiętając jednocześnie o zachowaniu warunku równowagi, możemy doprowadzić do tego, że parametr β bardzo dużo zmaleje.

Pomiar przeprowadzamy przy zasilaniu prądowym i wyjściu napięciowym, ze względu na najmniejsze β.

Układy:	β dla m≠1, n=1
I-U	½*1/(m+1)

W tym pomiarze m = 100, stąd β =½*1/(101). Zatem bardzo łatwo zauważyć, iż wartość ta jest ok. 50 razy mniejsza niż przy pomiarze 1.

Porównując otrzymane wartości błędów nieliniowości z pomiaru1 i 2 potwierdzamy, iż istotnie, zmieniając wartości rezystorów, lecz zachowując ich wzajemne stosunki zmniejszymy nieliniowość mostka.

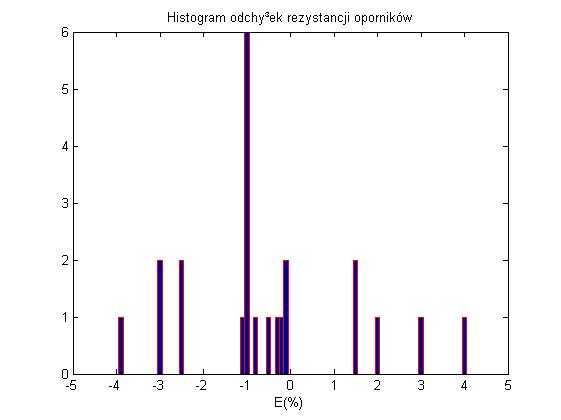
Pomiar 3: Odchyłki rezystancji oporników

Pomiary za pomocą fabrycznego mostka procentowego. Mierzymy wartości rzeczywistych odchyłek rezystorów od wartości nominalnej.

L.p.	[%]
1	-0,30
2	-0,20
3	3,00
4	-3,90
5	-3,00
6	-3,00
7	2,00
8	-2,50
9	-0,80
10	4,00
11	-1,00
12	-1,00
13	1,50
14	-0,50
15	-1,00
16	-1,00
17	1,50
18	-2,50
19	-0,10
20	-0,10
21	-1,10
22	-1,00
23	-1,00

W tym pomiarze zmierzyliśmy wartości rzeczywistych odchyłek rezystorów od wartości nominalnej i nanieśliśmy wartości tych odchyłek na osi liczbowej.

W przypadku, gdy chcemy dobrać pary rezystorów o najmniejszych odchyłkach operacja dotyczy większej liczby badanych rezystorów należy najpierw porównać je z jednym z rezystorów i rozdzielić na kupki, następnie wśród każdej kupki wybieramy jeden i postępujemy tak jak poprzednio, szukając pary, które najmniej się różnią.

4. Wnioski

• W ćwiczeniu poznaliśmy układ mostka odchyłowego, a także mostka procentowego.

• Największe odchyły zaobserwowaliśmy podczas badania rezystorów w układzie wejście napięciowe - wyjście prądowe. Najmniejsze zaś odchylenia występowały w przypadku układu wejście prądowe - wyjście napięciowe. W przypadku układów o jednakowym wejściu i wyjściu (napięciowe lub prądowe) zaobserwowaliśmy porównywalne wielkości odchyłu. Wywnioskować można z tego, że układ o wejściu prądowym i wyjściu napięciowym jest najlepszym do porównywania dwóch wielkości, jako najbardziej dokładny.

• Przyczyną różnic między względnymi błędami nieliniowości jest różnica parametrów β. Jest on najmniejszy dla układu I-U.

• Po zwiększeniu wartości rezystancji R₃ i R₄, stukrotnie zaobserwowaliśmy, że wychylenie zmniejszyło się do poziomu setnych procenta, co jest znacznie lepszym wynikiem niż poprzednie cztery pomiary. A więc, zwiększając m i n, można osiągnąć bardzo dobre wyniki. Nasze rozważania zostały potwierdzone w ćwiczeniu.

• Mostek procentowy okazał się bardzo przydatnym przyrządem do pomiaru odchyłek dużej liczby rezystorów. Jak pokazuje histogram rezystory mieszczą się w 5% - błędzie nieliniowości

8

Rysunek 1.

---