![]()
Momentem statycznym pola A względem pewnej osi nazywamy sumę iloczynów elementarnych pól A przez ich odległość od tej osi, obejmujące całe pole. Moment statyczny względem pewnej figury złożonej równa się sumie momentów statycznych jej części składowych względem tej osi. Położenie środka ciężkości pola figury płaskiej możemy wyznaczyć następującą zależnością: 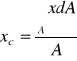
Momentem bezwładności pola A względem osi leżącej w jego płaszczyźnie nazywamy obejmująca całe to pole sumę iloczynów elementarnych pól dA przez ich odległość od tej osi. ![]()
![]()
Biegunowy moment bezwładności równa się sumie osiowych momentów bezwładności względem osi prostopadłej do siebie i przechodzącej przez dany biegun.
![]()
![]()
Odśrodkowym momentem bezwładności (moment dewiacji, zboczenia) pola A względem dwóch osi leżących w płaszczyźnie pola nazywamy obejmujące to pole sumę iloczynów elementarnych pól dA przez ich odległość od obu osi. ![]()
.Istnieje w każdym punkcie ciała układ osi względem, których moment dewiacji =0: - osie względem, których moment dewiacji =0 nazywamy głównymi osiami bezwładności, - moment bezwładności względem osi głównych osiągająca wartości ekstremalne nazywamy głównymi momentami bezwładności i oznaczamy I1 i I2 gdzie I1>I2. Promień bezwładności figury płaskiej względem danej osi x nazywamy wielkość, której kwadrat pomnożony przez pole tej figury daje moment bezwładności tej figury względem osi x.
1. Prostokąt : ![]()
![]()
2. Koło: ![]()
![]()
3. Pierścień: ![]()
![]()
4.Półkole: ![]()
![]()
5. Trójkąt: ![]()
![]()
![]()
WSKAŹNIKI WYTRZYMAŁOŚCI NIEKTÓRYCH FIGUR:
a)prostokąt ![]()
![]()
b)koło![]()
![]()
c)rurowy: ![]()
![]()
SKRĘCANIE, Jeżeli siły wewnętrzne redukują się do pary sił leżących w płaszczyźnie przekroju to mamy do czynienia ze skręcaniem. Podstawowe założenia teorii skręcania prętów osiowo symetrycznych: - przekroje płaskie przed skręceniem również po skręceniu są płaskie, - promienie naniesione na powierzchnię przekroju pozostają nieodkształcone - proste, - odległości między przekrojami nie ulegają zmianie. Przekroje obracają się jedynie względem siebie o niewielki kąt φ, - tworzące na powierzchni zmieniają się w linię śrubowe o kącie nachylenia γ do pierwotnego położenia, - materiał podlega prawu Hooke`a. Swobodne skręcanie prętów o przekroju nie kołowym, założenia de Saint - Venanta: - rzut konturu przekroju na płaszczyznę prostopadłą do osi pozostaje po skręceniu nieskręcony, - punkty leżące na płaszczyźnie przekroju mogą się swobodnie przemieszczać wzdłuż osi pręta. Założenie to dopuszcza możliwość wypaczenia (deklamacji) wyklucza natomiast występowanie naprężeń normalnych. Sprężyna śrubowo - walcowa: redukując siłę do środka przekroju widać, że stan naprężeń jest złożony. Przekrój drutu narażony jest na: - skręcanie ![]()
, - zginanie: ![]()
, - rozciąganie ![]()
, - ścinanie ![]()
dla małych kątów sinά=0, cosά=1 więc MS=PR i T=P
TWIERDZENIE STEINERA: Moment bezwładności Ix względem osi równy sumie momentów bezwładności względem osi przechodzących przez środek ciężkości JXC oraz iloczynu pola figury A i kwadratu odległości między tymi osiami a2. ![]()
![]()
![]()
ZGINANIE PRĘTA PROSTEGO: taki rodzaj obciążenia, przy którym w przekroju poprzecznym pręta występuje moment gnący. Jeżeli wektor gnący pokrywa się z główną osią bezwładności przekroju to zginanie nazywamy płaskim lub prostym. W innych przypadkach zginanie nazywa się ukośnym lub złożonym. Zginanie proste charakteryzuje się tym, że ugięta oś belki leży w płaszczyźnie działania obciążeń zewnętrznych. W przypadku gięcia złożonego płaszczyzna ugięcia osi belki nie pokrywa się z płaszczyzną działania obciążeń zewnętrznych. Wartość momentu gnącego w przekroju określa suma algebraiczna wszystkich momentów zewnętrznych i momentów od wszystkich sił działających na belkę z jednej strony rozpatrywanego przekroju obliczona względem środka tego przekroju. Wartość siły tnącej w przekroju określa suma algebraiczna wszystkich składowych poprzecznych sił działających na belkę z jednej strony rozpatrywanego przekroju. Wykresy sił tnących T i momentów gnących Mg, aby je wykonać należy: - ustalić przedmioty zmienności funkcji sił poprzecznych i momentów gnących, - wyznaczyć reakcję podpór, - ustalić analitycznie funkcję sił poprzecznych i momentów gnących we wszystkich przedziałach, - wyznaczyć konkretne wartości tych wielkości potrzebnych do sporządzenia wykresu, - sporządzić wykres. Czyste zginanie: Przypadek czystego zginania jest szczególnym przypadkiem zginania prostego. Występuje wtedy, gdy w przekroju belki na pewnej jej długości nie występują siły poprzeczne. Moment gnący zachowuje wtedy stała wartość wzdłuż osi belki. Istnieje warstwa włókien, która nie ulega ani skróceniu ani wydłużeniu warstwę tę nazywamy obojętną. Ślad warstwy obojętnej w przekroju poprzecznym nazywamy osią obojętną. Oś obojętna jest miejscem geometrycznym punktów przekroju, w których naprężenia są równe 0. Podstawowe założenia teorii zginania prętów prostych: - przy czystym zginaniu przekroje poprzeczne, które były płaskie również po odkształceniu pozostają płaskie, - włókna podłużne nie wywierają na siebie żadnego nacisku, a w związku z tym wskutek działania naprężeń normalnych doznaje jedynie jednoosiowego ściskania lub rozciągania, - odkształcenie włókien równoległych do osi pręta i znajdujących się w płaszczyźnie równoległej do warstwy obojętnej nie zależy od ich pól w tej płaszczyźnie, - materiał belki podlega prawu Hooke`a.
![]()
Z tego równania wynika, że moment statyczny przekroju względem osi obojętnej z=0 stad wniosek, że oś obojętna musi przechodzić przez środek ciężkości przekroju.
![]()
z tego równania wynika że moment zboczenia względem osi prostokątnych przekroju z których jedna jest osią obojętną i ma kierunek momentu gnącego (oś z) równy jest zero. Jest to warunek konieczny i dostateczny zginania prostego.
![]()
![]()
![]()
z tego równania: ![]()
![]()
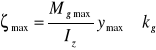
Wskaźnik wytrzymałości przekroju na zginanie:
![]()
Wprowadzone wzory odnoszą się do zginania czystego, a więc równomiernego. Jednak w praktyce stosuje się je również do zginania nierównomiernego, zakładając, że skutki działania siły poprzecznej i momentu gnącego można rozważać oddzielnie. Przy zginaniu z udziałem sił poprzecznych w przekroju obok naprężeń normalnych występują również naprężenia styczne, przy obliczeniach wytrzymałościowych przekrojów zwartych naprężenia styczne mogą być pominięte. Odgrywają one natomiast istotną rolę w przekrojach cienkościennych.
![]()
![]()
NAPRĘŻENIA STYCZNE PRZY ZGINANIU NIERÓWNOMIERNYM:, jeżeli moment gnący nie zachowuje wzdłuż osi pręta wartości stałej, to zginanie takie nazywa się nierównomierne. Gdy zmienność momentu wyrażona jest funkcją liniową miejsca wówczas siła poprzeczna T ma wartość stałą równą: Naprężenia normalne w dowolnym przekroju wyznacza się tak jak przy zginaniu równomiernym, a więc z zależności
Przyrost naprężeń normalnych obliczamy z zależności:
![]()
Warunek równowagi odciętej części elementu ma postać: ![]()
![]()
gdzie: b(y) - szerokość przekroju zależna od odległości od osi obojętnej.
Przyjmując założenia upraszczające że na powierzchni przekroju a1 , a1`, a2, a2` naprężenia styczne rozkładają się równomiernie, a więc τxy=τyx oraz przyjmując na podstawie tw o równowartości odpowiadających sobie naprężeń stycznych zależność τxy=τyx otrzymuje się: ![]()
UGIĘCIE I KĄT OBROTU PRZEKROJU BELKI:
W wyniku działania momentu gnącego zachodzi wzajemny obrót względem osi obojętnej uprzednio równoległych przekrojów. Odkształcenia te powodują zakrzywienie, czyli ugięcie prostej osi pręta. W zginaniu płaskim oś ugięta jest krzywą płaską.
1. Dla dowolnego przekroju belki przemieszczenie OO` środka ciężkości przekroju w kierunku prostopadłym do osi belki nazywa się ugięciem belki w tym przekroju.
2. Największe ugięcie belki w badanym przedziale zmienności funkcji y=f(x) nazywa się strzałką ugięcia f ymax = f
3. Kąt Θ, o jaki obróci się dany przekrój belki w stosunku do swojego pierwotnego położenia nazywa się kątem obrotu przekroju. Jest on równy kątowi nachylenia stycznej do linii ugięcia ![]()
Oś ugięcia belki opisuje równanie y=f(x) jej krzywiznę wyraża wzór: ![]()
(*)
Wzór ten nie uwzględnia siły poprzecznej na odkształcenia pręta. W większości zagadnień technicznych wpływ ten jest bardzo mały. Z geometrii różniczkowej krzywiznę dowolnej krzywej płaskiej y=f(x) przedstawia równanie:
![]()
![]()
(**)
z porównania równania (*) i (**) mamy:
![]()
![]()
W praktyce w skutek dużej sztywności prętów ich odkształcenia są małe, a promienie krzywizny osi ugiętej bardzo duże, w wyniku, czego przemieszczenie krzywizny osi
ugiętej są również bardzo małe, a więc: jest bardzo małe. Stąd:
![]()
Można, więc przyjąć, że:
Stąd też otrzymujemy równanie osi ugięcia pręta w postaci: ![]()
Znak + lub - jest zależny od ustalenia znaku momentu gnącego. Jeżeli moment będzie >0 to ![]()
jest to przybliżone równanie różniczkowe linii ugięcia.
WARUNKI BRZEGOWE: stałe C i D oblicza się z warunków brzegowych. Typowe warunki brzegowe do uproszczenia równania różniczkowego linii ugięcia są następujące:
UPROSZCZENIA W CAŁKOWANIU RÓWNANIA RÓŻNICZKOWEGO OSI UGIĘCIA W METODZIE CLEBSCHA
Dla belki ciągłej (bez przegubów) można uzyskać równość stałych całkowania dla wszystkich przedziałów (C1 = C2 = C) i (D1 = D2 =D), ale żeby to osiągnąć trzeba spełnić następujące warunki:
1)równania momentów gnących trzeba tak napisać, aby w równanie dla każdego nowego przedziału wchodziły wszystkie składniki równania dla poprzednich przedziałów. W tym celu należy przyjąć jeden dla wszystkich przedziałów układ osi o początku w jednym z końców belki.
2)jeżeli ai są współrzędnymi sił obciążających Pi lub początków obciążenia ciągłego qi to w warunkach typu Pi (x-ai) lub ½ qi (x-ai )2 nie należy rozwiać wyrażeń w nawiasach. Całkowanie prowadzi się według schematu ![]()
3)obciążenie ciągłe należy tak przestawić, aby każde obciążenie przebiegało aż do końca belki
4)w przypadku działania momentu skupionego należy wprowadzić w równanie momentów gnących również współrzędne tego momentu (dopisać ramię momentu do potęgi 0)
ROZWIĄZYWANIE BELEK STATYCZNIE NIEWZYNACZLNYCH
Można je rozwiązać opierając się na zasadach superpozycji. Metoda ta polega na rozłożeniu danego ukłonu hiperstatycznego na proste pomocnicze układu statycznie wyznaczalnego i następnie zastosowaniu superpozycji przemieszczeń w taki sposób, aby były spełnione warunki brzegowe dla układu wyjściowego.
Metoda porównywania ugięcia:
![]()
![]()
Metoda porównywania kątów ugięcia:
![]()
![]()
WYBOCZENIE SPRĘŻYSTE I NIESPRĘŻYSTE:
Wygięcie pręta spowodowane przekroczeniem przez siłę ściskającą wartości krytycznej nazywamy wyboczeniem. Rozróżniamy dwa rodzaje wyboczeń:
a) sprężyste - eulerowskie występuje ono wtedy gdy ![]()
gdzie: ![]()
b) sprężysto - plastyczne wtedy gdy ![]()
Przy obliczeniach prętów ściskanych należy zawsze uwzględniać 2 kryteria:
1)kryterium na wyboczenie ![]()
gdzie: ![]()
kw - dopuszczalne naprężenie na wyboczenie, nw - współczynnik bezpieczeństwa na wyboczenie
2)kryterium na ściskanie ![]()
gdzie: kc - dopuszczalne naprężenie na ściskanie ![]()
lub ![]()
w zależności od materiału.
Wyboczenie sprężyste: zakładamy, że ugięcie pręta jest, małe i odkształcenia są liniowo sprężyste. Równanie różniczkowe linii ugięcia ma postać:
![]()
![]()
![]()
stąd: ![]()
(*)
Warunki brzegowe:
1)x=0 y=0 => B=0 (0=Bcos0) => y=Asinkx
2)x=l y=0 => 0=Asinkl => k=(π/l)n
z równania (*) mamy: ![]()
dla n=1 mamy: ![]()
jest to najmniejsza wartość siły P dla której możliwe jest zachowanie równowagi pręta w postaci wygiętej jest to tzw. Eulerowskia siła krytyczna, dla tej wartości siły krytycznej równanie osi wygięcia przybiera postać: y=Asin(π/l)x oś ugięcia pręta jest sinusoidą.
Wyznaczenie siły krytycznej przeprowadzono dla pręta prostego obustronnego umocowanego przegubowo. Zmiana sposobu zamocowania wyraża się w zmianie warunków brzegowych wpływa na zmianą ostatecznego wzoru na siłę krytyczną. Wzór ma postać: 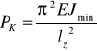
gdzie: lz=μL gdzie lz - długość zredukowana pręta, a μ - współczynnik zależy od sposobu zamocowania pręta.
Długość zredukowana jest to długość półfali, według której wybacza się pręt. Naprężenia krytyczne: ![]()
(*) gdzie : ![]()
λ - smukłość pręta
Smukłość pręta zależy od: 1) od sposobu zamocowania 2) od długości pręta 3) od kształtu i pola powierzchni przekroju poprzecznego. Smukłość nie zależy od rodzaju materiału. Ograniczenia stosowalności wzoru Eulera: wzór Eulera wyprowadzony został przy założeniu, że wyboczenie zaistnieje w obrębie ważności prawa Hooke`a. Nie można, więc się spodziewać praktycznego potwierdzenia tego wzoru dla naprężeń przekraczających granicę proporcjonalności RH.. Podstawiając we wzorze (*) za naprężenie σK=RH otrzymujemy:
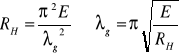
gdzie: λg - smukłość graniczna
Zależność naprężenia krytycznego od smukłości:
Prosta Tetmejera - Jasińskiego do granicy Re σK=a-bλ gdzie: dla stali λg = 100, dla żeliwa λg = 80 dla sosny λg = 110. dla smukłości większych od λg wyboczenie ma charakter sprężysty, a dla większych sprężysto - plastyczny. Jeżeli λ<λg to w obliczeniach na wyboczenie stosujemy wzory empiryczne: Tetmajera - Jasińskiego lub Johnsona - Ostenfilda. A) wzór Tetmajera - Jasińskiego ma postać σK=a-bλ jest to linia prosta, stałe a i b można znaleźć w poradnikach, ale można je również obliczyć ze znajomości Re i RH tak, że: a≈Re natomiast
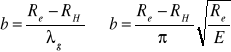
B) wzór Johnsona - Ostelfilda ma postać σK=A-Bλ2 stałe A i B wyznaczone doświadczalnie dla danego materiału.
Uwaga: dla dużych naprężeń ściskających i małych smukłości (dla stali praktycznie dla λ<25) w obliczeniach wytrzymałościowych pręty oblicza się wyłącznie z warunku na ściskanie.
![]()
![]()
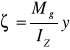
![]()
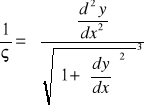
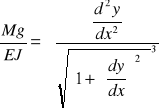
![]()
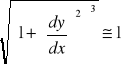
![]()
![]()
![]()
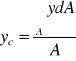
Wyszukiwarka
Podobne podstrony:
WTM 1, wytrzymałość materiałów
Laborki 2, Studia, Wytrzymałość materiałów II, Test z laborek wydymalka, lab
Laboratorium wytrzymałości materiałów
Wytrzymałość materiałów1 2 not
Wytrzymałość materiałów Ściąga 1
Mechanika i Wytrzymałość Materiałów zestaw2
A Siemieniec Wytrzymałość materiałów cz I (DZIAŁY PRZERABIANE NA PK WIITCH)
Mechanika i Wytrzymałość Materiałów W 1
test z wydymałki, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Wy
POMIAR TWARDOŚCI SPOSOBEM BRINELLA, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzy
Labora~3, Rok I, semestr II, Rok II, Semestr I, Wytrzymałość materiałów I, laborki - materiały + spr
L4 - pytania, Studia, Wytrzymałość materiałów II, lab4 wm2 studek
OPIS UK ADU UK KO OWY, wytrzymałość materiałów
cw-9 p, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Wytrzymałośc Materiałó
Spr. 1. Rozciąganie, Wytrzymałość materiałów
1 laborka -Układy liniowo sprężyste, Wytrzymałość materiałów(1)
A Siemieniec Wytrzymałość materiałów cz II
więcej podobnych podstron