SPIS TREśCI

Rozdział 1. Wstęp

Rozdział 1. Wstęp

Rozwiązując zadania matematyczne, przeważnie wykonujemy różne obliczenia, posługujemy się algorytmami i wzorami. Są jednak zagadnienia, które daleko prędzej i przejrzyściej można przedstawić i rozwiązać za pomocą rysunku. Treści zilustrowane obrazem graficznym są bardziej zrozumiałe i na dłużej zapadają w pamięci.

W moim opracowaniu przez graficzne rozwiązanie zadania rozumiem takie jego przedstawienie rysunkowe, które pomaga oddać i zrozumieć jego treść, a jego odpowiednie przekształcenie jest bezpośrednim rozwiązaniem, bądź w sposób oczywisty je wspomaga.

Zagadnienia prezentowane w mojej pracy dotyczą niektórych działów matematyki elementarnej. Mam nadzieję, że ich dobór przekona czytelników o użyteczności i skuteczności rysunkowego rozwiązywania zadań.

Rozdział 2. Graficzne sumowanie szeregów liczbowych

2.1. Suma kolejnych liczb naturalnych (

Chcemy znaleźć sumę liczb: 1+2+3+...+n = ?

Czy istnieje prostszy sposób niż kolejne sumowanie tych liczb?

Przyjmijmy, że sumowanie liczb zastępujemy sumowaniem kwadracików, przy czym liczbie 1 odpowiada jeden kwadracik (guzik, kulka, itp.).

1+2=3 1+2+3=6 1+2+3+4=10 1+2+3+4+5=15 1+2+...+n=
+

Policzyć sumę to obliczyć połowę pola kwadratu o boku równym n i dodać do niej n- „połówek” kwadracików jednostkowych.

Możemy też postąpić inaczej: do figury będącej sumą pól kwadracików „dołożyć” figurę do niej przystającą, w wyniku czego otrzymujemy prostokąt o bokach: n i n+1. Szukana suma to połowa pola tego prostokąta.

Nietrudno zauważyć, że to ten sam wynik.

2.2. Suma liczb naturalnych parzystych (

; n
N )

2+4+6+...+2n=? n=1,2,3 ...

2+4=6 2+4+6=12 2+4+6+8=20 2+4+6+...+2n=n(n+1)

Suma liczb parzystych od 2 do 2n to pole prostokąta o bokach n i n+1

2.3. Suma liczb naturalnych nieparzystych (
)

1+3+5+7+...+2n-1=? n=1,2,3,...

1+3=4 1+3+5=9 1+3+5+7=16 1+3+...+2n-1=n2

Suma liczb nieparzystych od 1 do 2n-1 to pole kwadratu o boku n.

Otrzymane wzory rekurencyjne dowodzi się indukcyjnie.

2.4. Suma szeregów geometrycznych malejących

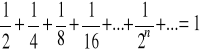
Przyjmijmy, że wyrazom odpowiadają pola prostokątów, kolejny wyraz jest połową poprzednika :

Sumę szeregu odnajdujemy jako sumę pól odpowiednich prostokątów.

Nietrudno zauważyć, że suma szeregów o ilorazie równym
równa jest podwójnej wartości pierwszego wyrazu, ale czy tak jest zawsze?

Rozważmy sumę szeregu:

S₁=

Aby upewnić się że szukana suma to 1/2 rozważmy szereg w którym iloraz też wynosi 1/3, ale liczniki to dwójki:

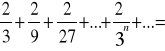
S₂

S₂=1

Wobec faktu że każdy wyraz został powiększony dwukrotnie suma S₂ musi być też dwukrotnie większa od S₁.

S₁=
S₂=

Przy stałej szeregu równej 1/3 sumę szeregu możemy otrzymać przez pomnożenie pierwszego wyrazu przez odwrotność dopełnienia stałej do jedynki.

S₁=

S₂=

Przy stałej szeregu równej 1/2, dopełnienie do 1 też wynosi 1/2, jego odwrotność 2/1 i sumy trzech pierwszych szeregów spełniają „odkryty” algorytm:

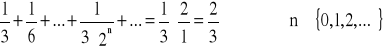
Zweryfikujmy otrzymany przepis na sumę dla szeregów o stałej 1/4.

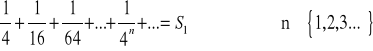
Takie sumowanie nie daje jednoznacznej odpowiedzi jaką częścią kwadratu jest suma kolejnych wyrazów, czyżby sformułowany algorytm nie był słuszny?

Rozważmy inny szereg o tym samym „odstępie” równym 1/4.

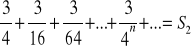
Suma tego szeregu jednoznacznie zmierza do 1 i spełnia algorytm: pomnóż pierwszy wyraz przez odwrotność dopełnienia stałej do 1.

Z uwagi na fakt, że wyrazy tworzące sumę S₁ są trzykrotnie mniejsze od wyrazów tworzących sumę S₂ możemy stwierdzić, że:

S₁=

Algorytm na szukanie sumy szeregu został „uratowany”. Zauważmy, że podobny sposób „ratowania” algorytmu wystąpił przy sumie szeregów:

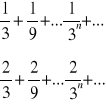
Pierwszy wyraz szeregu, który „ratuje” przepis rozpoczyna się od wyrazu będącego dopełnieniem do jedynki pierwszego wyrazu szeregu „ratowanego” . Sprawdzimy regułę „ratowania” przepisu na sumę szeregów o stałej wynoszącej 1/5 :

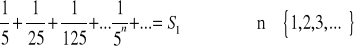
Z takiego obrazu geometrycznego trudno dociec do czego zmierza suma wyrazów szeregu. Weźmy więc szereg o tej samej stałej, w którym pierwszy wyraz jest dopełnieniem 1/5 do 1 przy tej samej stałej:

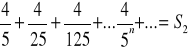
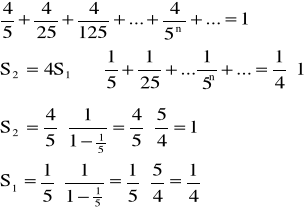
Przepis na szukanie sumy jeszcze raz został obroniony. Powstaje pytanie po co szukać graficznie sumy szeregu geometrycznego skoro można ją znaleźć algebraicznie:

a₁ + a₁q + a₁q² + ... a₁qⁿ + ... = S / ^. q

a₁q + a₁q² + ... a₁qⁿ⁺¹ + ... = Sq

S - Sq = a₁

S (1 - q) = a₁

Argumenty przemawiające za graficznym szukaniem sumy szeregów geometrycznych :

1. Poglądowość i przejrzystość metody;

1. Nie potrzeba umiejętności rozwiązywania i przekształcania równań;
   

Braki:

1. Z graficznego sumowania nie zawsze jednoznacznie wynika do czego zmierza suma -istotnym jest wybór pola powierzchni figury na podstawie którego określamy sumę;

1. Przybliżoność metody.

Wniosek:

Graficzny obraz działania może naprowadzić na sformułowanie algebraicznego przepisu .

Rozdział 3. Podstawowe działania arytmetyczne

Graficzne dodawanie, odejmowanie, mnożenie, dzielenie i pierwiastkowanie jest systemem konstrukcji, które z pewnym przybliżeniem zastępują operacje rachunkowe.

Liczby rzeczywiste dodatnie, które poddajemy działaniu zastępujemy czynnościami graficznymi na odcinkach, których długości wyrażają się tymi liczbami.

3.1. Dodawanie

Niech a i b będą liczbami rzeczywistymi większymi od zera. Dodać te liczby to z odcinków o długości a i b zbudować odcinek, który jest ich sumą.

Z dowolnego punktu M. prowadzimy półprostą i na niej odmierzamy odcinek MN o długości a, a na jego przedłużeniu odcinek NP. o długości b. Odcinek MP jest sumą odcinków, a jego długość jest sumą długości a+b. Mierząc długość MP znajdujemy sumę a+b.

Dodawanie odcinków, podobnie jak dodawanie liczb jest przemienne i łączne.

3.2. Odejmowanie

Niech a i b będą liczbami rzeczywistymi większymi od zera. Odjąć od liczby a liczbę b to z odcinków o długościach a i b zbudować odcinek, który jest ich różnicą.

1). a>b

Z dowolnego punktu K prowadzimy półprostą i odmierzamy na niej odcinek KL o długości a, a na tym odcinku od końca L w stronę K odcinek LM o długości b. Odcinek KM jest różnicą odcinków, a jego długość - poszukiwaną różnicą a-b.

2). a=b

Wynikiem odjęcia odcinków o równych długościach jest odcinek, którego końce pokrywają się - czyli punkt (odcinek o długości 0).

3). a<b

W zbiorze liczb rzeczywistych nieujemnych działanie niewykonalne, podobnie jak dla odcinków (długość jest liczbą nieujemną).Odcinek MK można zinterpretować jako dopełnienie odcinka a do b (brakujący odcinek), używanie liczb ujemnych jako wyniku takiego odejmowania może stać się jednym z faktów przemawiających za rozszerzeniem liczb dodatnich.

3.3. Dzielenie i mnożenie

Jednym z praktycznych zastosowań twierdzenia Talesa jest graficzne określenie ilorazu i iloczynu długości odcinków. Niech a, b będą długościami odcinków, a 1 to odcinek jednostkowy przy czym a i b > 0. W celu wykreślenia odcinka o długości a/b rysujemy dowolny kąt AOC, którego miara jest różna od 0 i od ∏.

Na jego ramionach odkładamy odcinki AO = a i OC = b. Na odcinku OC (dzielniku) odkładamy odcinek jednostkowy OB = 1, łączymy punkt A z C i z punktu B rysujemy prostą równoległą do AC. Odcinek OD ma długość a/b.

Gdy a=b wynikiem dzielenia jest odcinek jednostkowy odpowiadający liczbie 1.

Konstrukcję odcinka a b przedstawiają rysunki.

3.4. Pierwiastkowanie. Pierwiastek stopnia drugiego

Graficzne określenie pierwiastka kwadratowego z danej liczby jako konsekwencja rozwiązania następującego zadania:

Z kwadratu, którego bokiem jest suma dwóch odcinków o długościach a i b „odetnij” cztery przystające do siebie trójkąty prostokątne o długościach przyprostokątnych a i b. Oblicz pole powierzchni figury powstałej po odcięciu, wyrażone wielkościami a i b.

Z faktu przystawania trójkątów prostokątnych o długości przyprostokątnych a i b wnioskujemy:

1. Wszystkie boki czworokąta są sobie równe, a ich długość to długość przeciwprostokątnej tych trójkątów ;

1. Wszystkie kąty wewnętrzne czworokąta są kątami prostymi.

Otrzymany czworokąt jest kwadratem, w którym boki są przeciwprostokątnymi trójkątów prostokątnych o długościach przyprostokątnych a i b.

Szukane pole - część niezakreślona rysunku to długość przeciwprostokątnej podniesiona do kwadratu. Oznaczmy długość przeciwprostokątnej przez X

P= X²

Z drugiej strony „składając” dwie pary trójkątów prostokątnych wzdłuż przeciwprostokątnej i odsuwając je wzajemnie jak wyżej dostajemy :

P² = a² +b²

Kwadrat, którego bokiem jest przeciwprostokątna trójkąta prostokątnego ma takie samo pole powierzchni jak suma pól kwadratów, których bokami są przyprostokątne tego trójkąta ( Tw. Pitagorasa). Związek ten wykorzystamy do wyznaczenia pierwiastka kwadratowego z liczb dodatnich całkowitych

Wyciągnąć pierwiastek to narysować trójkąt prostokątny taki, by suma kwadratów długości przyprostokątnych była równa liczbie pierwiastkowanej. Mierząc długość przeciwprostokątnej takiego trójkąta znajdujemy przybliżoną wartość pierwiastka kwadratowego.

Wyznaczmy pierwiastki kwadratowe kolejnych liczb naturalnych:

Rozbudujemy trójkąt prostokątny równoramienny o jednostkowej długości ramion tak, że jedno z nich pozostaje stałe, a otrzymane przeciwprostokątne stają się przyprostokątnymi wyznaczającymi kolejne przeciwprostokątne tj. szukane pierwiastki kwadratowe.

Takie postępowanie jest czasochłonne, zwłaszcza wtedy gdy poszukiwane są pierwiastki z większych liczb naturalnych. Możemy ją zmodyfikować w przypadku konkretnej liczby.

Wyznaczmy pierwiastek kwadratowy z liczby 41:

Nie zawsze liczba pierwiastkowana daje się rozłożyć na sumę dwóch czy trzech „kwadratów”, czasem rozkładanie jest bardziej pracochłonne, ale też prowadzi do celu np:

79 = 64+15 = 64+9+6 = 64+9+4+2 = 8²+3²+2²+1²+1²

lub 79 = 36+25+9+9 = 6²+5²+3²+3²

Wyrażając liczby pierwiastkowane jako wielokrotności lub podwielokrotności liczb z, których pierwiastek jest „wyciągalny”, najczęściej: 100 lub 10000 metodę możemy rozszerzyć na duże liczby naturalne bądź liczby mniejsze od 1.

Np.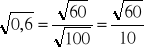

Wystarczy „wyciągnąć” graficznie pierwiastek z 60 - zmierzyć i przesunąć przecinek w lewo o jedno miejsce.

Wyciągnąć pierwiastek z 12 i przesunąć przecinek w prawo o jedno miejsce.

Skuteczność metody zawodzi gdy liczbę pierwiastkowaną nie uda się przedstawić jako wielokrotność lub podwielokrotność 100 lub 1000. Weźmy liczbę 3,45: przeskalowanie niewiele pomoże bo musimy „wykreślić” pierwiastek z 345 i podzielić przez 10. Z kłopotów mogą wybawić dwa fakty:

1. Kąt wpisany oparty na średnicy okręgu jest kątem prostym;

1. Podobieństwo trójkątów prostokątnych wyznaczonych przez wysokość trójkąta prostokątnego poprowadzoną z wierzchołka kąta prostego.

Niech a - długość odcinka, z którego wyciągamy pierwiastek, a 1 - długość odcinka jednostkowego. Sumujemy odcinki a i 1. Następnie rysujemy okrąg, którego średnicą jest znaleziona suma. z końca odcinka a wystawiamy prostą prostopadłą do średnicy okręgu. Punkt przecięcia tej prostej z okręgiem i koniec odcinka a wyznaczają odcinek, którego długość jest poszukiwaną wartością pierwiastka kwadratowego.

**** =
bo oparty na średnicy;

* *** * * ***

więc wnosimy, że trójkąty ABD i DBC są podobne

Stąd:

Takim algorytmem poszukiwania pierwiastka możemy objąć szerszy zakres liczb, choć oczywiście nie wszystkie. Musimy jednak pamiętać o ograniczonym stopniu dokładności konstrukcji i odczytu. Powróćmy do pierwiastka z liczby 3,45. Niech liczbie tej odpowiada odcinek o długości 3,45 cm. Przyrządy zwykle używane pozwolą narysować tylko odcinek o długości 3,5 cm przy jednostce 1 cm i oszacować -pierwiastek:

1,8 *
* 1,9

3.5. Działania łączne

Zwykle takie przybliżone oszacowanie w arytmetyce szkolnej jest wystarczające, a pozwala uniknąć żmudnych rachunków zwłaszcza gdy liczby wymierne poddajemy działaniom łącznym.

Np.

Wartość metody graficznej obliczania wartości wyrażeń polega na jej łatwości i poglądowej przejrzystości, wyraźnym brakiem jest niezbyt duża dokładność. W wielu jednak przypadkach : praktyce geodezyjnej, statyce graficznej ta dokładność obliczeń jest wystarczająca, ponieważ dane wielkości, którymi te obliczenia operują , już są przybliżone i przez to samo wpływają na małą dokładność odpowiedzi.

Rozdział 4. Przekształcenia algebraiczne

Algebra z uwagi na fakt posługiwania się symbolami jest najtrudniej przyswajalnym działem matematyki elementarnej, dlatego też należy starać się stworzyć sytuację problemową, w której posługiwanie się literą ma dla uczniów sens i umożliwia im samodzielne działanie. Sytuacją taką jest na pewno obliczanie pola powierzchni prostokąta o długościach boków x i y.

Umiejętność obliczania pola powierzchni prostokąta można wykorzystać przy mnożeniu sum i różnic wyrażeń algebraicznych.

4.1. Mnożenie sum algebraicznych

Zadanie 1.

W prostokącie, którego boki mają długość x i y wydłużono jedną parę boków równoległych o 2. Oblicz pole powstałej figury.

• wydłużamy o 2 boki x, y pozostaje stałe:

P = y(x + 2), ale też P = xy + 2y więc: y(x + 2) = xy+2y

• wydłużamy o 2 boki y, x pozostaje stałe

P = x(y+2), ale też P = xy + 2x więc: x(y + 2) = xy + 2x

Zadanie 2.

W prostokącie, którego boki mają długość x i y zwiększono jedną parę boków o długość a. Oblicz pole powstałej figury. Z uwagi na niejednoznaczną treść zadania, możliwe są trzy rozwiązania:

• zwiększamy parę boków równoległych x o a:

P = y(x + a), ale też P = yx + ya

więc: y(x + a) = yx + ya

• wydłużamy drugą parę boków równoległych y o a

P = x(y + a), ale też P = xy + xa

więc: x(y + a) = xy + xa

• wydłużamy parę boków prostopadłych x i y o a

P = (y + a) (x + a), ale też P = yx + ya + ax + a²

Zadanie 3.

W prostokącie o bokach długości x i y wydłużono odpowiednio pary boków równoległych o a i b. Oblicz pole powstałej figury.

P = (x + a) (y + b) jak też P = xy + xb +ay + ab

więc (x + a) (y + b) = xy + xb + ay + ab

4.2. Mnożenie różnic i sum przez różnice algebraiczne

W podobny sposób można otrzymać pola powierzchni prostokątów o skróconych bokach:

y(x - a) = yx -ya

Określając zależności pomiędzy polami prostokątów o zmienionych wymiarach wykazujemy jednocześnie słuszność rozdzielności mnożenia względem dodawania i odejmowania - opusz- czenie nawiasów staje się łatwiejsze. Poważnym brakiem wykorzystania pól prostokątów do określania iloczynów różnic wyrażeń algebraicznych są sytuacje , w których długość boku prostokąta skracanego jest mniejsza od długości, o którą chcemy go skrócić. Kłopotliwym wyjściem staje się wtedy operowanie brakującymi polami - prostokątami dopełniającymi.

4.3. Wzory skróconego mnożenia

Wykorzystując umiejętność wyrażania zmian pola powierzchni prostokąta jako funkcji zmian długości jego boków - możemy graficznie „wyprowadzić” wzory skróconego mnożenia:

1. (a + b)² = a² + 2ab + b²

2. (a - b)^{2 =} a² - 2ab + b²

3. (a - b)(a + b) = a² - b²

Wzory te otrzymujemy zwykle wykorzystując rozdzielność mnożenia względem dodawania lub odejmowania. Równie dobrym sposobem na ich otrzymanie i zapamiętanie jest rysunek.

Ad. I. Narysuj kwadrat o boku a, następnie wydłuż jego boki o b. Określ pole otrzymanej figury.

Otrzymujemy kwadrat o długości boków: a+b

Kwadrat ten można „rozciąć” na dwa kwadraty

o bokach a i b i dwa przystające prostokąty o bo-

kach a i b. (a + b)² = a² + b² + 2ab

Ten sam wzór możemy wyrazić „w drugą stronę”: z dwóch kwadratów o bokach a i b oraz dwóch prostokątów o bokach a i b można ułożyć kwadrat o boku a+b.

Wzór I przedstawia kwadrat sumy dwóch liczb. Graficznie można sformułować wzór na kwadrat sumy trzech, czterech i więcej liczb.

(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac.

Z rys. możemy otrzymać też wzory dodatkowe:

(a + b + c)² = (a + b)² + 2(a + b)c + c²

(a + b+ c)² = (b + c)² + 2(b + c)a + a²

(a+b+c+d)² = a² + b² + c² + d² + 2ab +2ac + 2ad + 2bc + 2bd + 2cd

Tu też możemy wyprowadzić dodatkowe wzory:

(a+b+c+d)² = (a+b)² + (c+d)² + 2(a+b)(c+d)

(a+b+c+d)² = (a+b+c)² + 2(a+b+c)d + d²

(a+b+c+d)² = (b+c+d)² + 2(b+c+d)a + a²

Ad. II Boki kwadratu skracamy o tę samą długość. Przyjmując, że zmniejszenie nie może przekroczyć długości boku skróconego tzn. a>b

Otrzymujemy kwadrat o długości boków: a-b, którego pole równe jest :

(a-b)² = a² +b² - 2ab

Odcinając z kwadratu o boku a dwa przystające prostokąty o bokach a i b (odrzucamy „niepotrzebnie”: kwadrat o boku b) otrzymujemy kwadrat o boku a-b

Po modyfikacji rysunku:

Jeżeli od sumy pól dwóch kwadratów o długościach boków a i b odejmiemy pola dwóch przystających prostokątów o długościach boków a i b to otrzymamy pole kwadratu, którego bok ma długość a-b.

W przypadku gdy a=b, kwadrat redukuje się do punktu, a tożsamość jest oczywista.

Ad. III. Parę boków równoległych kwadratu o boku a wydłużamy, o b, a drugą parę boków skracamy o tę samą długość.

Pole prostokąta, którego bokami są: suma i różnica długości a i b (a>b) równe jest różnicy pól kwadratów o bokach a i b.

„W drugą stronę”:

Odcinając z kwadratu o boku a kwadrat o boku b otrzymujemy prostokąt, którego bokami są :
a+b i a-b.

Wzory algebraiczne wyrażone rysunkiem możemy wykorzystać w rozwiązywaniu zadań:

Zadanie 1.

Jak zmieni się pole kwadratu gdy długość jego boków :

1. zwiększymy lub zmniejszymy dwukrotnie;

2. zwiększymy lub zmniejszymy trzykrotnie;

3. zwiększymy lub zmniejszymy n-krotnie, n-liczba naturalna

Ad. 1a)

Ad. 1b)

Zadanie 2.Który z prostokątów o takim samym obwodzie ma największe pole powierzchni?

Rozwiązanie pierwsze: Korzystamy z faktu, że wydłużając jedną parę boków równoległych prostokąta o określoną długość i jednocześnie skracając drugą parę boków o tyle samo to obwód prostokąta nie zmienia się.

1). Wydłużamy bok dłuższy o 1i skracamy bok krótszy o 1. Ubytki pola - S (strata) , zyski pola- Z. Bilansujemy zyski i straty: S - Z = [b -(a -1)] 1.

2). Wydłużamy bok b o 2 i skracamy bok a o 2. Bilans pola jeszcze bardziej niekorzystny: S- Z = [b- (a - 2)] ^. 2

3). Zwiększenie i zmniejszenie boków o 3, bilans jeszcze bardziej niekorzystny: S - Z = [b - (a - 3)] ^. 3.

Im bardziej „wydłużony” prostokąt tym ma mniejsze pole.

Zobaczmy co się stanie gdy będziemy skracać bok dłuższy, a wydłużać bok krótszy o określoną długość x.

Nietrudno zauważyć, że maksymalne pole powierzchni będzie mieć prostokąt, w którym wszystkie boki mają tą samą długość, a więc kwadrat:

b - x = a + x

Jednoczeœnie otrzymaliśmy przepis: jak prostokąt zamienić na kwadrat o takim samym obwodzie. Wystarczy jego dłuższe boki skrócić o połowę różnicy długości jego boków, a boki krótsze wydłużyć o te same wartości.

Boki tak otrzymanego kwadratu mają długość:

(a + b)

Rozwiązanie drugie: Za punkt wyjścia obieramy kwadrat, w którym bok ma np. 5 jednostek długości. Zmieniamy skokowo jego rozmiary o tę właśnie jednostkę. Zliczając kwadraciki jednostkowe wyrażające pole powierzchni powstałych prostokątów zauważymy, że:

• w kwadracie mieści się ich 25;

• w prostokącie „zmienionym” o 1 jednostkę: 24;

• w prostokącie „zmienionym” o 2 jednostki: 21;

• w prostokącie „zmienionym” o 3 jednostki: 16;

• w prostokącie „zmienionym” o 4 jednostki: 9:

Wniosek podobny jak w rozwiązaniu pierwszym.

Rozważania zmiany pola kwadratu możemy uogólnić na kwadrat o dowolnej długości boku a i zmianie wymiarów o: k, 2k, 3k, ...

Otrzymujemy „na nowo” wzór skróconego mnożenia:

Wydłużając parę boków równoległych kwadratu o boku a o określoną długość x i jednocześnie skracając drugą parę o tyle samo, otrzymujemy prostokąt, którego pole jest mniejsze od pola kwadratu o pole równe kwadratowi, którego boki mają długość x.

Zadanie 3.

Cena większości towarów jest wprost proporcjonalna do ich ilości. Wyjątkiem jest diament. Diament dwa razy cięższy kosztuje cztery razy drożej, trzy razy cięższy - dziewięć razy drożej, itd. Słowem - wartość diamentu jest wprost proporcjonalna do kwadratu jego masy. Podczas szlifowania bryłka rozpada się na dwie części. Jak wielka jest strata szlifierza? w jakim przypadku strata jest największa?

Rozwiązanie. Wartość diamentu zależy od jego masy tak samo jak pole powierzchni kwadratu zależy od długości jego boku. Skoro tak to przedstawmy masę diamentu jako odcinek o długości x, a jego wartość kwadratem o tej długości boków:

Ponieważ wartość diamentu jest wprost proporcjonalna do kwadratu masy to po rozpadzie na dwie części o masie b i c wartość jest równa sumie pól kwadratów o długościach boków b i c (część zakreskowana):

W = b² + c²

Pole dwóch przystających prostokątów o długościach boków b i c odpowiada stratom:

S = 2bc

Straty będą największe gdy prostokąty te będą miały maksymalne pole powierzchni.

Strata jest największa gdy prostokąt o długościach boków b i c jest kwadratem:

b = c =
x

Fakt jest znany - pole prostokąta o ustalonym obwodzie jest największe gdy jest on kwadratem Maksymalna strata wartości diamentu przy jego rozpadzie na dwie części powstaje wtedy gdy części te są jednakowe.

S_max = 2
x²

S_max =
x²

Wartość minimalna W_min =
b². Przy takim rozpadzie wartość diamentu spada dwukrotnie.

W podobny graficzny sposób można rozpatrzyć rozpad diamentu na 3 i więcej części:

Rozpad na 3 części: x = a + b + c; W = a² +b² + c²; S = 2(ab + bc + ac).

Straty w tym przypadku to suma pól trzech par przystających prostokątów. Strata będzie maksymalna gdy staną się one przystającymi do siebie kwadratami:

a = b = c =
x; S_max = 6
x²

S_max =
x² W_min =
x²

Diament przy rozpadzie na 3 równe części traci trzykrotnie na wartości.

Rozpad na 4 części:

x = a + b +c + d

S = (ab + ac + ad + bc + bd + cd)

Straty maksymalne: gdy prostokąty strat stają się przystającymi kwadratami:

a = b = c = d =
x

S_max = 12
x² =
x²

W_min =
x²

Straty wartości diamentu rosną ze wzrostem ilości części na które się rozpada. Maksymalne straty powstają przy rozpadzie na równe części, diament traci na wartości tyle razy ile jest tych równych części.

Rozdział 5. Zakończenie

Nie sposób przecenić graficznego ujęcia niektórych zagadnień matematyki elementarnej. Obok niewątpliwych zalet do których należą:

• konkretyzacja obiektów poddanych działaniu;

• poglądowość i przejrzystość czynności;

• w miarę proste przekształcenia ;

• unikanie żmudnych rachunków;

• szybkość obliczeń;

• łatwość zapamiętania i odtwarzania;

ma i wady, o których należy pamiętać:

• ograniczony zakres wielkości poddanych działaniu;

• mała dokładność obliczeń;

• zawężone możliwości wykonywania obliczeń.

Rozstrzygnięcie: rysunek czy rachunek, nie może być jednoznaczne. Myślę, że obydwa środki nawzajem się uzupełniają i przeplatają. Skuteczne nauczanie nie może obejść się, ani bez jednego, ani bez drugiego.

LITERATURA:

1. Zofia Krygowska - „Zarys dydaktyki matematyki”, WSiP Warszawa 1969.

1. W. Warwick Sawyer - „Myślenie obrazowe w matematyce elementarnej”, Wiedza Powszechna Warszawa 1988.

1. F. Van Dieven-Thomas, Nicolas Rouche, Josse Ottevaere, Medeleine Vilanon-Schul -
   „En question de question”; Wydawnictwo- Didier Hatier 1995.

1. Tadeusz Rams - „O prezentacji graficznej sum”- „Matematyka” nr 2-3/90.

1. Mirosław Dąbrowski - „O historii odkrycia niewymierności” - „Matematyka” nr 2/86.

1. Wacław Zawadowski - „Nauczanie matematyki w klasie szóstej”; WSiP Warszawa 1983.

1. Cecylia Rauszer - „Rozmaitości matematyczne”; IW „Nasza Księgarnia” Warszawa 1983.

1. Stanisław Kowal - „Przez rozrywkę do wiedzy”; Wydawnictwa Naukowo-Techniczne Warszawa 1971.

1. Gustaw Treliński, Eugeniusz Wachnicki - „Podręcznik dla klasy siódmej szkoły podstawowej”; WSiP Warszawa 1987.

26

METODY GRAFICZNE MATEMATYKI ELEMENTARNEJ

n

5

4

3

2

n

5

4

3

2

n

n+1

4

5

3

4

2

3

1+2=(2 ^.3)/2

1+2+3+=(3 ^.4)/2

1+2+...+n=n^. (n+1)/2

1+2+3+4=(4 ^.5)/2

3

4

5

n+1

n

4

3

2

n

2

3

4

2

3

4

n

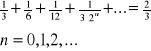
a₁ - pierwszy wyraz szeregu

q - stała szeregu

S - suma szeregu

P

N

M

a+b

b

a

b

K

L

M

b

a

a-b

b

a

K

M

L

b

a

L

K

M

O

X

X

a

a

b

b

=

=

x

x

a

a

b

b

a²

b²

x

b

a

1

5

2

6

4

D

B

1

C

A

a

3,5

1

1

1

6,5

1

x

x

y

y

2

x+2

y+2

x

x

y

y

2

x

y

a

x+a

x

y

a

y+a

x

y

a

a

x+a

y+a

x

y

a

b

y-b

x

x

y

y

x-a

(x - a) (y - b) = xy + ab - ay - xb.

Czynnik ab pojawia się z uwagi na fakt, że odejmując od pola xy pola ay i bx odjęliśmy za dużo pole ab

e.

Mnożąc sumę przez różnicę otrzymujemy:

(x + a) (y - b) = xy - bx + ay - ab

x

x

x

y

y

y

a

a

a

b

b

b

x-a

x-a

y-b

y-b

Podobny rezultat otrzymamy, modyfikując poprzedni rysunek

a+b

a

a

b

b

a+b

a

a

b

b

c

c

a²

b²

c²

ab

ab

ac

ac

bc

bc

a+b+c

a

b

c

a²

a²

a²

b²

b²

d

a²

b²

c²

d²

ab

ab

ac

ac

ad

ad

bc

bc

bd

bd

cd

cd

c

d

a

b

b

b

b

a

a

a

a-b

a-b

a-b

(a-b)²

a

b

a+b

a-b

a-b

a-b

lub

b

b

b

b

b

b

b

a

a

a

a

P₁ : P₂ = 1 : 4

a

a

a

a

a

a

a²

P₁

P₂

P₁ : P₂ = 1 : 9

P₁ : P₂ = 1 : n²

Zwiększając (zmniejszając) bok kwadratu
n-razy, zwiększamy (zmniejszamy) jego pole
n²-razy.

a

a

a

a

a

a

a²

P₁

P₁

P₂

n ^. a

n ^. a

P₂

b+1

a

a-1

b

S

1

Z

a-3

b+2

b+3

a

a-2

b

S

S

Z

Z

a

a

b

b

x

x

x

x

x

x

b-a

1/2(b-a)

1/2(a+b)

a

a

a²

a²-k²

a²-4k²

a²-9k²

k

2k

3k

Rozpad na dwie części:

x = b + c

straty

masa

x

x

wartość- x²

c

b

b

c

straty

b²

c²

x

b

b

b

b

b

b

c

c

c

c

c

c

S

S

S

S

S_max

S_max

x

b

b

c

c

S

S

x

S_max

S_max

S_max

S_max

S_max

S_max

c

b

a

a

b

c

S

S

S

S

S

S

a²

b²

c²

x

S_max

S_max

S_max

S_max

S_max

S_max

S_max

S_max

S_max

S_max

S_max

S_max

a

a

d

c

b

b

x

c

S

S

S

S

S

S

S

S

S

S

S

S

a²

b²

c²

d²

d

x

x

---