Przestrzeń liniowa (przestrzeń wektorowa)

Niech K będzie ciałem, niech V - będzie niepustym zbiorem, w którym określone jest działanie wewnętrzne + oraz działanie zewnętrzne zwane mnożeniem przez elementy z ciała K oraz wyróżniony jest element 0∈V.

Elementy zbioru V będziemy nazywać wektorami, wektor 0 nazywamy wektorem zerowym, zaś elementy ciała K będziemy nazywać skalarami.

Przestrzenią liniową (bądź przestrzenią wektorową) rozpiętą nad ciałem K nazywamy strukturę algebraiczną (V, K, +, ) , jeśli spełnione są następujące warunki (aksjomaty przestrzeni liniowej) dla dowolnych wektorów a, b, c ∈ V i dowolnych skalarów α, β ∈ K:

1. (V, +) jest grupą przemienną, jej element neutralny nazywamy zerem przestrzeni liniowej i oznaczamy 0;

2.

3.

4.

5.

Uwaga !

1. Przestrzeń liniową i jej zbiór wektorów będziemy oznaczać tym samym symbolem V

2. (V, R, +, ) - oznacza przestrzeń liniową rzeczywistą

3. (V, C, +, ) - oznacza przestrzeń liniową zespoloną

Przykłady

Niech E¹ oznacza prostą euklidesowa,

E² - oznacza płaszczyznę euklidesową,

E³ - oznacza trójwymiarową przestrzeń euklidesową. Stąd Eⁿ oznacza przestrzeń euklidesową dla n∈{1,2,3}.

Niech p∈Eⁿ , S_P(Eⁿ) oznacza zbiór wektorów związanych (zaczepionych) w punkcie p wraz z działaniami :

+ - dodawania wektorów zaczepionych w punkcie p,

- mnożenia wektora zaczepionego w punkcie p przez liczbę rzeczywistą,

oraz wyróżnionym wektorem zerowym 0_p zaczepionym w punkcie p.

Można sprawdzić, że (S_p(Eⁿ), R, +, ) - jest przestrzenią wektorowa (przestrzenią wektorową rzeczywistą).

Przypomnieć definicję dodawania wektorów zaczepionych oraz mnożenia wektora zaczepionego przez liczbę rzeczywistą.

Wektory zaczepione (o początkach) w różnych punktach przestrzeni Eⁿ można porównywać, stąd wprowadza się relację równoważności takich wektorów, którą będziemy oznaczać ≡ .

Relacja równoważności wektorów zaczepionych jest relacją równoważnościową.

Dowód samodzielnie przygotować.

Czyli: [p₁q₁]_≡ = p₁q₁ , to znaczy: klasę abstrakcji wektora zaczepionego p₁q₁ względem relacji równoważności takich wektorów będziemy nazywać wektorem swobodnym p₁q₁ .

Niech S(Eⁿ) oznacza zbiór wektorów swobodnych przestrzeni euklidesowej Eⁿ dla n∈{1, 2, 3}. Wówczas można sprawdzić, że (S(Eⁿ), R, +, ) jest przestrzenią wektorową.

Niech Kⁿ = {(a₁, a₂, …, a_n): a_i ∈K dla i∈{1, .. , n}}, gdzie n jest ustaloną liczbą naturalną.

Niech a, b ∈ Kⁿ ; czyli a = (a₁, a₂, …, a_n),

b = (b₁, b₂, …,b_n), gdzie a_i, b_i ∈ K dla i∈{1, …, n} , oraz λ ∈ K.

Nadto przyjmijmy, że:

Wówczas łatwo sprawdzić, że : (Kⁿ, K, +,  jest przestrzenią liniową nad ciałem K , a zerem tej przestrzeni jest ciąg (0, 0, …, 0) ∈ Kⁿ , którą nazywa się: n wymiarową przestrzenią liniową nad ciałem K.

Analogicznie wyodrębnia się nieskończenie wymiarową przestrzeń liniową nad ciałem K , czyli przestrzeń liniową postaci: (K^∞, K, +, ).

Jej wektory utożsamiamy z nieskończonymi ciągami o elementach z ciała K : np. a ∈ K^∞ , czyli

a = (a₁, a₂, …, a_n, …) , gdzie a_i ∈ K dla i ∈ N; 0 ∈ K^∞ , czyli 0 = (0, 0, …, 0, …) .

Analogicznie wyodrębnia się przestrzenie wektorowe: (Rⁿ, R, +, ) oraz (R^∞ , R, +, ) .

Niech A≠∅ oraz V będzie przestrzenią liniową nad ciałem K. Niech dla f, g ∈ V^A oraz α ∈ K:

(f+g)(x) = f(x) + g(x) dla dowolnego x ∈A ,

(α f)(x) = α f(x) dla dowolnego x ∈ A .

Wówczas łatwo sprawdzić, że : (V^A, K, +, ) jest przestrzenią liniową zwaną przestrzenią liniową wszystkich funkcji określonych na zbiorze A o wartościach w przestrzeni V.

Przygotować samodzielnie poniższe ćwiczenia i zadania.

Niech (V^A, K, +, ) będzie przestrzenią liniową nad ciałem K .

1. Wskazać zero tej przestrzeni liniowej .

2. Kiedy dana przestrzeń liniowa będzie przestrzenią liniową z przykładów 3, 3', 3'' .

Skonstruować przestrzeń liniową liczb zespolonych (krótko: przestrzeń liniową R² nad R).

Niech (V, K, +, ) będzie przestrzenią liniową nad ciałem K. Wykazać że :

1) 1 a = a dla a∈V , 1 ∈ K;

2) α 0 = 0 dla α ∈ K, 0 ∈ V.

Liniowa zależność i liniowa niezależność wektorów

Niech (V, R, +, ) będzie przestrzenią liniową nad ciałem R oraz u₁, u₂, …,u_n ∈ V ; α₁, α₂, …, α_n ∈ R.

Kombinację liniową wektorów u₁, u₂, …, u_n o współczynnikach α₁, α₂, ..., α_n ∈ R nazywamy wektor u postaci : u = α₁u₁ + … + α_nu_n .

Mówimy, że wektory u₁, u₂, …, u_n tworzą układ wektorów liniowo zależny (są liniowo zależne) w przestrzeni V wtw, gdy istnieje ciąg skalarów α₁, α₂, ..., α_n ∈ R, które nie wszystkie są zerami i takie, że kombinacja liniowa α₁u₁ + … + α_nu_n jest wektorem zerowym.

Stąd: wektory u₁, u₂, …,u_n są liniowo zależne ⇔

Mówimy, że wektory u₁, u₂, …, u_n przestrzeni V tworzą układ wektorów liniowo niezależny (są liniowo niezależne) wtw, gdy nie jest to układ liniowo zależny.

Stąd: wektory u₁, u₂, …, u_n są liniowo niezależne

Jeśli wektor u jest kombinacją liniową wektorów
u₁, u₂, …, u_n , to mówi się, że wektor u zależy liniowo od wektorów u₁, u₂, …, u_n .

Przykłady

Niech u₁ = (1,0) ∈ R² ; u₂ = (1,0) ∈ R² . Wykażę, że wektory u₁, u₂ są liniowo niezależne w przestrzeni liniowej (R², R, +, ) nad ciałem R.

Istotnie : jeśli α₁u₁ + α₂u₂ = 0 , to α₁=α₂=0 .

Skoro (α₁ 1+α₂ 0, α₁ 0 + α₂ 1) = (0,0) , to α₁ =0 ∧ α₂=0, cnd.

Niech z₁ = 5 + 2i ; z₂ = 3 + i ; z₃ = 2 - 3i ∈C . Wykażę, że wektory z₁, z₂, z₃ są liniowo zależne w przestrzeni liniowej (C, R, +, )

Rozważmy dowolną kombinację liniową postaci :

α₁z₁ + α₂z₂ + α₃z₃ i przyrównajmy ją do wektora zerowego:

α₁z₁ + α₂z₂ + α₃z₃ = 0

Stąd otrzymujemy :

5α₁ + 3α₂ + 2α₃ + (2α₁ + α₂ - 3α₃)i = 0 + 0 i

Stąd dla t ≠ 0: α₁²+α₂²+α₃² > 0 ∧ , cnd.

Układ wektorów złożony z wektora u = 0 jest liniowo zależny, bo dla α ≠ 0 zachodzi warunek : α 0 = 0.

Natomiast układ wektorów złożony z wektora u ≠ 0 jest liniowo niezależny, bo: jeśli α u = 0 , to α = 0.

Na to, aby układ wektorów u₁, u₂, …, u_n był liniowo zależny potrzeba i wystarcza, by jeden spośród nich był liniowo zależny od pozostałych.

Dowód oczywisty: samodzielnie przygotować!

Każdy podukład liniowo niezależnego układu wektorów jest liniowo niezależny. Każdy układ wektorów zawierający liniowo zależny podukład jest liniowo zależny. Każdy zależny układ wektorów zawiera skończony zależny podukład.

Dowód oczywisty!

Baza przestrzeni liniowej (przestrzeni wektorowej)

Baza przestrzeni liniowej to jest układ liniowo niezależny wektorów tej przestrzeni liniowej, który generuje ją .

Niech (V, K, +, ) będzie przestrzenią liniową nad ciałem K (w szczególności K=R lub K=C) .

Układ A=(a_t)_t∈T , gdzie T⊂N ∧ T≠∅, wektorów przestrzeni liniowej V nad ciałem K nazywamy bazą przestrzeni V , gdy :

1. układ A jest liniowo niezależny wektorów;

2. każdy układ zawierający układ A i różny od A jest układem liniowo zależnych wektorów.

Uwaga 1: Układ (a_t)_t∈T wektorów przestrzeni liniowej V nad ciałem K jest podzbiorem wektorów tej przestrzeni liniowej

Uwaga 2: Analogicznie definiuje się liniową zależność oraz liniową niezależność wektorów a₁, a₂, …, a_n; bądź układu wektorów A=(a_t)_t∈T przestrzeni liniowej

(V, K, +, ), tak jak w przestrzeni liniowej (V, R, +, ).

Jeśli V jest niezerową przestrzenią liniową nad ciałem K, zaś A=(a_t)_t∈T jest układem wektorów przestrzeni V, to następujące warunki są równoważne :

1. 
   układ A wektorów jest bazą przestrzeni V;

2. 
   układ A wektorów jest układem liniowo niezależnym wektorów i każdy wektor a∈V jest kombinacją liniową wektorów układu A ;

3. 
   każdy wektor a∈V można i to tylko na jeden sposób przedstawić jako kombinację liniową wektorów układu A.

Dowolny niepusty podzbiór U przestrzeni liniowej (przestrzeni wektorowej) V nad ciałem K (w szczególności K=R lub K=C) nazywamy podprzestrzenią przestrzeni V, gdy U jest przestrzenią liniową nad ciałem K z tymi samymi działaniami.

W szczególności: jeśli (V, R, +, ) jest przestrzenią liniową, zaś U={α₁u₁+α₂u₂+…+α_nu_n : α₁, α₂,…, α_n ∈R}, gdzie u₁∈V, …, u_n∈V są ustalonymi wektorami przestrzeni V, to (U, R, +, ) jest podprzestrzenią przestrzeni liniowej V.

Sprawdź to!

Najmniejszą podprzestrzeń liniową zawierającą wszystkie wektory u₁, u₂, …, u_n ; bądź wszystkie wektory układu A = {u₁, u₂, …, u_n} nazywamy podprzestrzenią rozpiętą na tych wektorach, bądź podprzestrzenią generowaną przez te wektory, bądź ich otoczką liniową, i oznaczamy lin(u₁, u₂, …, u_n); bądź span A; bądź vect A.

Wymiar przestrzeni liniowej

Jeżeli przestrzeń liniowa V ma bazę skończoną, to mówimy, że ta przestrzeń jest skończenie wymiarowa, a liczbę elementów tej bazy nazywamy wymiarem przestrzeni liniowej V i oznaczamy dimV.

Natomiast, jeśli dana przestrzeń V nie ma skończonej bazy, to mówimy, że jej wymiar jest nieskończony i piszemy wówczas: dim V = ∞.

Jeśli V = {0}, to bazą przestrzeni V jest zbiór pusty; zaś wymiar tej przestrzeni jest 0.

Komentarz dydaktyczny

Baza przestrzeni liniowej generuje tę przestrzeń.

Baza n-wymiarowej przestrzeni liniowej V nad ciałem R pozwala ustalić odwzorowanie przestrzeni V w Rⁿ .

Niech B={u₁, u₂, …, u_n} będzie bazą n-wymiarowej przestrzeni V oraz w ∈ V.

Wówczas na podstawie odpowiednich twierdzeń istnieje dokładnie jeden układ skalarów (α_i)_i∈T , T = {1, …, n} taki, że: , gdzie α_i ∈R dla i∈T.

Niech S: V→Rⁿ oraz S(w) = (α₁, α₂, …, α_n)

Skalary α₁, α₂, …, α_n∈R nazywamy współrzędnymi (bądź układem współrzędnych) wektora w w bazie B={u₁, u₂, …, u_n} przestrzeni liniowej V, natomiast skalar α_i dla dowolnego i ∈ {1, 2, …, n} nazywa się i-tą współrzędną wektora w w tej bazie.

Zmiana bazy przestrzeni liniowej powoduje zmianę współrzędnych danego wektora w tej przestrzeni liniowej.

Rozwiązać samodzielnie poniższe ćwiczenia:

Ćwiczenie 1: Sprawdzić, że:

1. A ⊂ span A; 2) span( span A) = span A;

3) A ⊂ B ⇒ span A ⊂ span B;

4) (span A)∪(span B) ⊂ span(A∪B).

Ćwiczenie 2: Sprawdzić, że każdy zbiór wektorów przestrzeni liniowej jest albo zbiorem wektorów liniowo zależnych, albo niezależnych tej przestrzeni.

Baza kanoniczna przestrzeni liniowej (Rⁿ,R, +, )

Baza kanoniczna przestrzeni liniowej (Rⁿ,R, +, ) to jest układ wektorów e₁, e₂, …, e_n , gdzie

e_i = (0, 0, …, 1, 0, …, 0) dla i∈{1, 2, …, n}

Wówczas dowolny wektor w ∈ Rⁿ można przedstawić w postaci :

.

Czyli w = (α₁, α₂, …, α_n) ∈ Rⁿ , zaś liczby (skalary): α₁,…, α_n ∈ R nazywają się współrzędnymi wektora w w bazie kanonicznej przestrzeni Rⁿ nad ciałem R.

Zadanie: Wykazać, że: wektory a₁, a₂, a₃ ∈ R³ tworzą bazę przestrzeni liniowej R³ nad ciałem R, gdy

a₁ = (1, 0, 1); a₂ = (2, -3, 0); a₃ = (0, 5, 2). Wyznaczyć współrzędne wektora x=(3, 2, 3) ∈ R₃ w bazie a₁, a₂, a₃ .

Dla rozwiązania tego zadania wystarczy wykazać iż: jeśli każda kombinacja liniowa α₁a₁ + α₂a₂ + α₃a₃ = 0 , to α₁=α₂=α₃=0 oraz dowolny wektor a ∈ R³ jest kombinacją liniową wektorów a₁, a₂, a₃ , czyli wektorów bazy tej przestrzeni.

Dla wyznaczenia współrzędnych danego wektora x w bazie a₁, a₂, a₃ wystarczy rozwiązać układ równań postaci:

α₁a₁ + α₂a₂ + α₃a₃ = x
ze względu na niewiadome α₁, α₂, α₃ .

Przestrzeń euklidesowa

Przestrzeń euklidesowa to jest przestrzeń liniowa

(V, R, +, ) wyposażona w mnożenie skalarne (iloczyn skalarny) wektorów.

Niech x, y ∈ V , α ∈ R. Jeśli dowolnej uporządkowanej parze wektorów (x, y) z przestrzeni V przyporządkujemy liczbę rzeczywistą oznaczoną x y tak by spełnione były następujące warunki dla dowolnych

x, y ∈V i dowolnego α ∈ R:

1) x y = y x ;

2) α(x y) = αx y ;

3) (x + y) z = x z + y z ;

4) x x ≥ 0 ;

5) jeśli x ≠ 0 , to x x > 0 ;

to mówimy , że określony został iloczyn skalarny x y wektorów x, y z przestrzeni V.

Wektory x i y ∈ V nazywamy wektorami ortogonalnymi, gdy x y = 0. Stąd, w szczególności wektor zerowy jest ortogonalny do każdego wektora.

Uwaga ! Pojęcie oraz nazwa iloczynu skalarnego wektorów pochodzi od matematyka irlandzkiego W.R. Hamiltona (1805 - 1865) .

Uwaga ! Warto wspomnieć, że za pomocą iloczynu skalarnego wektorów można zdefiniować ważne w matematyce pojęcie normy wektora x , które będziemy oznaczać x ;przy czym : dla x ∈ V.

Przestrzeń wektorową, w której określono iloczyn skalarny wektorów, nazywamy przestrzenią euklidesową.

Mówimy, że w przestrzeni wektorowej V nad ciałem R określona jest norma , jeśli każdemu wektorowi x tej przestrzeni wektorowej przyporządkowana jest liczba rzeczywista x , przy czym przyporządkowanie to spełnia poniższe trzy warunki dla dowolnych x, y ∈ V i dowolnego α ∈ R :

N1) x = 0 ⇔ x = 0 ;

N2) αx = α x ;

N3) x + y ≤ x + y .

O przestrzeni, w której określona jest norma, mówimy, że jest unormowana.

Nieskończenie wymiarowe przestrzenie unormowane (zupełne) badał Stefan Banach (1892 - 1945). Na cześć tego wielkiego matematyka polskiego przestrzenie te nazwano przestrzeniami Banacha.

Rozwiązać samodzielnie poniższe ćwiczenia :

Korzystając z definicji iloczynu skalarnego udowodnić nierówność Schwarza:

(x y)² ≤ (x x) (y y)

Wykazać, że spełnia warunki definicji normy oraz nierówność x ≥ 0 .

Wykazać, że: jeśli x y =0 , to x ² + y ² = x + y ²

(czyli udowodnić twierdzenie Pitagorasa).

Z nierówności Schwarza wynika poniższa nierówność:

dla dowolnych niezerowych wektorów x i y .

Stąd poprawna jest następująca definicja cosinusa kąta między niezerowymi wektorami:

Przykład

Niech (V, R, +, ) będzie przestrzenią liniowa z bazą:

u₁, u₂, …, u_n oraz x, y ∈ V. Wówczas: x = x₁u₁ + … + + x_nu_n ; y = y₁u₁ + … + y_nu_n. Stąd iloczyn skalarny wektorów x i y można określić następująco :

Sprawdź, że tak określony iloczyn skalarny wektorów spełnia warunki definicji (aksjomatycznej definicji) iloczynu skalarnego wektorów przestrzeni V.

Wówczas norma wektora x ∈ V może być określona wzorem:

i zależy tylko od współrzędnych wektora x w danej bazie przestrzeni V.

Odwzorowania liniowe

Niech (U, R, +, ) , (V, R, +, ) to są przestrzenie wektorowe oraz T: U → V

Odwzorowanie T: U→V nazywamy odwzorowa-niem liniowym przestrzeni wektorowej (przestrzeni liniowej) U w przestrzeń V, gdy:

1) ; tzn. T jest addytywne ;

2) ; tzn. T jest jednorodne.

Rozwiązać samodzielnie poniższe zadania:

Niech T: R³ → R³ ∧ T(x, y, z) = (x, y + z, x + z),

S: R³ → R³ ∧ S(x, y, z) = (x, y², z²),

1. Sprawdź, czy odwzorowania T i S są liniowe ?

2. Wyznaczyć: S + T, ST, TS, kerS, kerT oraz (o ile istnieją) S^-1, T^-1.

Niech u₁, u₂, …, u_n będą wektorami przestrzeni wektorowej V nad ciałem R.

Zdefiniować następujące pojęcia:

1. układ ortogonalny (układ ortonormalny) wektorów, przestrzeni V,

2. symbol Kroneckera δ_ij dla i, j ∈ {1, 2, …, n} .

Poniższe spostrzeżenia (tw.) opisują najważniejsze własności odwzorowań (przekształceń) liniowych:

Odwzorowanie liniowe przestrzeni U w przestrzeń V jest homomorfizmem przestrzeni U w przestrzeń V.

Dowód: Tj. oczywiste!; sprawdź.

Odwzorowanie liniowe przekształca (przeprowadza) wektor zerowy na wektor zerowy.

Dowód: T(0) = T(0 x) = 0 T(x) = 0

Obrazem podprzestrzeni przez odwzorowania liniowe jest podprzestrzeń.

Dowód: Niech E będzie podprzestrzenią przestrzeni U oraz T jest odwzorowaniem liniowym przestrzeni U w przestrzeń V oraz y, y₁ ∈ T(E). Istnieją wówczas x, x₁∈E takie, że T(x) = y , T(x₁) = y₁ .

Mamy więc dla dowolnych α, β ∈ R:

αy + βy₁ = αT(x) + βT(x₁) = T(αx + βx₁) ∈ T(E)

Ponadto 0 = T(0) ∈ T(E) , cnd.

Przeciwobraz podprzestrzeni przez odwzorowanie liniowe jest podprzestrzenią.

Dowód: Niech T: U → V będzie odwzorowaniem liniowym, zaś W jest podprzestrzenią przestrzeni V oraz x, x₁ ∈ T^-1(W). Mamy zatem: T(αx + βx₁) = αT(x) + +βT(x₁) ∈ W, bo T(x), T(x₁) ∈ W.

Stąd αx + βx₁ ∈ T^-1(W). Ponadto 0 ∈ T^-1(W), bo T(0)=0, cnd.

Niech T: U → V będzie odwzorowaniem liniowym przestrzeni U w przestrzeń V.

ImT = T(U) = {T(x): x ∈U} - to jest obraz odwzorowania liniowego (ImT jest podprzestrzenią T(U)).

kerT = {x∈U: T(x) = 0} = T^-1({0}) ten zbiór nazywamy jądrem odwzorowania liniowego T.

Rzędem odwzorowania liniowego T nazywamy wymiar jego obrazu ImT i oznaczamy go rgT. Stąd: rgT=dim(ImT).

Rozwiązać samodzielnie poniższe zadania:

1. Zbadać, że f(x,y) = (2x-y, x+3y-1, 5x+2y) nie jest przekształceniem liniowym przestrzeni R² w przestrzeń R³.

2. Wykazać, że T(x,y) = (3x+5y-2z , 2x-y) jest prze-kształceniem liniowym oraz wyznaczyć : kerT, ImT, rgT.

2

14



Df

1



Ćww

df

Tww

df





2

K

n

n

n

n

df



df

Tw



df

śr.



df

ozn

Df

Df

2

1°

Df





1

i - ta współrzędna wektora e_i



x

i

i



x

3'











3"

4



Ćw

Zad.

Zad.





Ćw2





Df

Df

Df



Df



3°

Df



df



Df

Df

2°





1













2



, gdzie t∈R









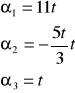
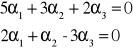
3

Tw.









Tw

Tw

Df







1



Df

x

x

y

n

y

i

i

i

n



cos

Df

(

x

Df

Df

df

y

Ćw1

y

x



y





Df







Ćw3

1

1

,

)













df







Zad 1

Zad 2



1

2



3

x

y

x

y

x



4

x

x

x

5°

Def

4°

Def

Df

Def

2

1

2

1

2

2

1

1

p

q

q

p

q

p

q

p







śr.





a

b

a

b

a

b

a

b

3









)

,

,

(

2

2

1

1

,

n

K

a

a

a

a







)

,

,

,

(

2

1





































x

x

x







---