POLITECHNIKA ŚLĄSKA W GLIWICACH

WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA

kierunek: Zarządzanie i Inżynieria Produkcji

Model ekonometryczny

Wykonał: Krystian Mrowiec

Grupa: ZIP 22

Liczba urodzeń w Polsce w latach 1990-2004

Wykonany przez mnie model ma na celu pokazanie jakie elementy mają wpływ na liczbę urodzeń w latach 1990 - 2004r.

Dane do modelu zebrałem na podstawie danych źródłowych z Roczników Statystycznych Głównego Urzędu Statystycznego, a przy tworzeniu modelu korzystałem z programu Microsoft Excel.

Tabela 1 Dane do modelu

Lata	Y	X1	X2	X3	X4	X5
1990	551,2	255,4	9,4	139,5	102,9	1591,70
1991	551,5	233,2	9,5	136,8	177,0	2155,39
1992	518,7	217,3	9,7	133,0	293,5	2996,10
1993	497,7	207,7	9,8	94,4	399,5	4050,50
1994	485,1	207,7	9,9	76,1	532,8	5459,00
1995	436,3	207,1	10,0	67,1	702,6	7938,00
1996	431,2	203,6	10,1	62,1	873,0	9981,00
1997	415,2	204,8	10,2	73,7	1061,9	12144,00
1998	398,1	209,4	10,2	80,6	1239,5	14211,00
1999	384,4	219,4	10,2	82,0	1706,7	15913,37
2000	380,5	211,2	10,1	87,8	1923,8	16953,82
2001	370,2	195,1	10,1	106,0	2061,9	18646,51
2002	355,5	191,9	10,0	97,6	2133,2	20339,20
2003	352,8	195,4	9,9	162,7	2201,5	22031,89
2004	356,0	196,0	9,9	108,1	2289,6	23724,59

Y - liczba urodzeń [tyś.osób]

X1 - liczba zawartych małżeństw [tyś]

X2 - liczba kobiet w wieku rozrodczym [tyś.osób]

X3 - liczba mieszkań oddanych do użytku [tyś.sztuk]

X4 - przeciętne miesięczne wynagrodzenie brutto [zł]

X5 - PKB na 1 mieszkańca w zł

Współczynniki korelacji

Aby obliczyć współczynniki korelacji korzystamy z następujących wzorów:

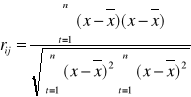
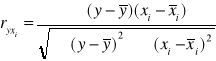
Otrzymujemy wektor R₀ oraz macierz współczynników korelacji:

Tabela 2 Wektor R0

0,770792

-0,77467

0,233819

-0,9541

-0,96622

Tabela 3 Macierz współczynników

	X1	X2	X3	X4	X5
X1	1	-0,67592	0,314483	-0,68063	-0,70145
X2	-0,675925	1	-0,69372	0,59062	0,609797
X3	0,3144829	-0,69372	1	-0,00615	-0,0288
X4	-0,680634	0,59062	-0,00615	1	0,989802
X5	-0,701446	0,609797	-0,0288	0,989802	1

Metoda Hellwiga

W modelu ekonometrycznym powinny znaleźć się zmienne, które są odpowiednio silnie skorelowane ze zmienną objaśnianą Y. W celu wyeliminowania z modelu zmiennych, które mają słaby wpływ na zmienną objaśniana stosuje się metodę Hellwiga.

Na początku obliczam ilość kombinacji zmiennych objaśniających x₁, x₂, x₃, x_4, x₅ według wzoru L=2^k-1, gdzie k to ilość zmiennych objaśniających.

L = 2^k-1 = 2⁵-1 = 31 kombinacji

Następnie obliczam pojemność indywidualną i integralną z następujących wzorów korzystając z wcześniej obliczonych współczynników korelacji:

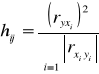
Wypisuję wszystkie możliwe kombinacje, obliczam indywidulane pojemności nośników, wchodzących w skład kombinacji, następnie sumuje

K1={X1}, K2={X2}, K3={X3}, K4={X4}, K5={X5}, K6={X1,X2}, K7={X1,X3}, K8={X1,X4}, K9={X1,X5}, K10={X2,X3}, K11={X2,X4}, K12={X2,X5}, K13={X3,X4}, K14={X3,X5}, K15={X4,X5}, K16={X1,X2,X3}, K17={X1,X2,X4}, K18={X1,X2,X5}, K19={X1,X3,X4}, K20={X1,X3,X5}, K21={X1,X4,X5}, K22={X2,X3,X4}, K23={X2,X4,X5}, K24={X3,X4,X5}, K25={X2,X3,X5}, K25={X1,X2,X3,X4}, K27={X1,X2,X3,X5}, K28={X1,X3,X4,X5}, K29={X2,X3,X4,X5}, K30={X1,X2,X4,X5}, K31={X1,X2,X3,X4,X5}

Po zsumowaniu indywidualnych pojemności nośników otrzymałem:

H1	0,579477
H2	0,596247
H3	0,051686
H4	0,77171
H5	0,784376
H6	0,69953
H7	0,476738
H8	0,851598
H9	0,846502
H10	0,38671
H11	0,970147
H12	0,977242
H13	0,719582
H14	0,729656
H15	0,785181
H16	0,567967
H17	0,927242
H18	0,784343
H19	0,81079
H20	0,925194
H21	0,781056
H22	0,866616
H23	0,817155
H24	0,9773
H25	0,771694
H26	0,823724
H27	0,822452
H28	0,959518
H29	0,832686
H30	0,877997
H31	0,887082

Wybieram kombinację, która ma najwyższą wartość; jest to tzw. kombinacja optymalna

K MAX =	0,977242

Z metody Hellwiga wynika, że do modelu wchodzą zmienne x_2, x₅ ponieważ K MAX to K₂₈={x_2, x₅}. Oznacza to, że zmienne x₂, i x₅ mają duży wpływ na zmienną objaśnianą.

Równanie modelu ma postać:

y=α₀+α₁x₂i+α₂x₅i+εi

Metoda grafów

Wykorzystując wektor R₀ oraz macierz współczynników korelacji dokonuję wyboru zmiennych za pomocą metody grafów.

  0,05

n-2=30

Liczę krytyczną wartość współczynnika korelacji, korzystając przy tym z tablic rozkładu t-Studenta.

tα- odczytujemy z tablic tα= 2,042

r*= 0,492803263

W macierzy współczynników korelacji należy zastąpić zerami wszystkie współczynniki korelacji, które są mniejsze od r*. W ten sposób otrzymuję macierz R*

	X1	X2	X3	X4	X5
X1	1	0,680734	0	0,586649	0,611163
X2	0,680734	1	0,6755	0	0
X3	0	0,6755	1	0	0
X4	0,586649	0	0	1	0,981818
X5	0,611163	0	0	0,981818	1

Na podstawie danych z powyższej macierzy buduję graf:

Zgodnie z założeniami metody grafów do modelu wchodzi zmienna x5, gdyż jest najsilniej skorelowana ze zmienną objaśnianą.

Metoda Najmniejszych Kwadratów (MNK)

Aby oszacować parametry strukturalne korzystam ze wzoru:

Następnie tworzę macierze X i Y

	1	9,4	1591,70			551,2
	1	9,5	2155,39			551,5
	1	9,7	2996,10			518,7
	1	9,8	4050,50			497,7
	1	9,9	5459,00			485,1
	1	10,0	7938,00			436,3
X=	1	10,1	9981,00		Y=	431,2
	1	10,2	12144,00			415,2
	1	10,2	14211,00			398,1
	1	10,2	15913,37			384,4
	1	10,1	16953,82			380,5
	1	10,1	18646,51			370,2
	1	10,0	20339,20			355,5
	1	9,9	22031,89			352,8
	1	9,9	23724,59			356

Kolejno obliczam:

	15	149	178136,0685
X^TX=	149	1480,92	1785509,299
	178136,069	1785509,299	2924727581

	175,7093	-18,09293748	0,0003436
(X^TX)^-1=	-18,09294	1,865603179	-3,69426E-05
	0,000344	-3,69426E-05	1,96728E-09

	6484,4
X^TY=	64220,72
	69671314,7

Podstawiając do wzoru otrzymuję wektor parametrów strukturalnych:

	1367,24687
a=	-85,304676
	-0,00737586

Równanie modelu ma zatem postać:

Yi=1367,24687 - 85,304676X2i - 0,00737586X5i

Następnie obliczam:

- wariancję S_e²

- odchylenie standardowe reszt Se

- współczynnik zmienności resztowej W_e

- współczynnik determinacji R²

- współczynnik zbieżności φ²

Obliczam wariancję S_e² oraz odchylenie standardowe S_e ze wzorów:

Se^2=	69,1685054
Se =	8,31676051

Współczynnik zmienności resztowej V_e. Informuje on o tym, jaką część wartości średniej Y stanowi odchylenie standardowe reszt. V_e powinno być bliskie 0, aby stwierdzić, że weielkość S_u jest odpowiednio mała. Obliczamy go według wzoru:

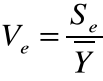
V_e= 0,0192386971250004

Oznacza to, że dany model jest wyjaśniony w 1,92%

Ocena dopasowania modelu do danych empirycznych ma na celu sprawdzenie czy model w wystarczającym stopniu wyjaśnia kształtowanie się zmiennej objaśnianej. Dopasowanie można obliczyć za pomocą następujących współczynników, które przyjmują wartości z przedziału <0,1>.

Współczynnik determinacji R² informuje, jaka część zmiennej objaśnianej Y została objaśniona przez zbudowany model teoretyczny. Dopasowanie modelu do danych empirycznych jest tym lepsze, im współczynnik determinacji bliższy jest wartości 1. Obliczam go korzystając ze wzoru:

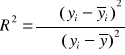
R² = 0,9883

Model jest dopasowany do danych empirycznych w ok. 98,83%

Współczynnik zbieżności φ² informuje, jaka część zmienności zmiennej objaśnianej Y nie została wyjaśniona przez zbudowany model teoretyczny (jest spowodowana przez czynnik losowy). Dopasowanie modelu do danych empirycznych jest tym lepsze, im współczynnik zbieżności jest bliższy 0. Obliczam go korzystając ze wzoru:

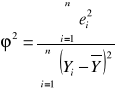
φ ² = 0,0117

Model jest niedopasowany do danych empirycznych w ok. 1,17%

MACIERZ WARIANCJI I KOWARIANCJI OCEN PARAMETRÓW STRUKTURALNYCH

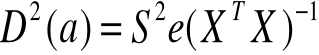
Z macierzy wariancji i kowariancji, wyrażonej poniższym wzorem, szacuję średnie błędy szacunku parametrów:

	12153,5523	-1251,461443	0,023766325
D^2(a)=	-1251,46144	129,0409835	-0,002555265
	0,02376633	-0,002555265	1,36074E-07

Następnie obliczam błędy szacunku parametrów strukturalnych

D(a0)=	110,2432
D(a1)=	11,35962
D(a2)=	0,000369

Postać modelu w przypadku błędów strukturalnych:

Yi= 1367,24687-85,304676X2i-0,00737586X5i
	110,2432	11,3596		0,0004

TEST ISTOTNOŚCI WSPÓŁCZYNNIKA KORELACJI WIELORAKIEJ (próba Fishera)

Stawiam hipotezy:

H₀ : R² = 0

H1 : R² ≠ 0

Obliczam F ze wzoru:

F = 508,896982

Dla α=0,05, k=2 i n-k-1=12 odczytuję F* z tablic Fishera

F* = 3,89

F > F* - odrzucamy hipotezę H₀

WERYFIKACJA MODELU

Po oszacowaniu modelu należy zbadać, czy zbudowany model dobrze opisuje badane zależności, a dzieje się to za sprawą weryfikacji modelu.

TEST LOSOWOŚCI

Test losowości ma na celu zbadanie trafności doboru zmiennych do modelu.

Stawiam hipotezę:

H₀ : rozkład jest liniowy

H₁ : rozkład jest nieliniowy

Następnie tworzę serie, czyli przyporządkowuję każdej reszcie dodatniej literę a, zaś każdej reszcie ujemnej literę b.

-2,44276552	b
10,54539958	a
1,007292505	a
-3,685135039	b
2,634228795	a
-19,3505512	b
-0,851205363	b
7,633243458	a
5,77914229	a
4,635581959	a
-0,120703519	b
2,064367346	a
-8,681048169	b
-7,426454297	b
8,258607181	a

b	aa	b	a	bb	aaa	b	a	bb	a
1	2	3	4	5	6	7	8	9	10	k=10

Otrzymałem 10 serii, czyli k = 10

Następnie obliczam ilość dodatnich i ujemnych reszt:

a = 8 = n₁ b = 7 = n₂

Z tablic testu liczby serii odczytuję wartości krytyczne K_l (0,025) i K_p (0,975) dla:

α=0,05, n₁ i n₂

K_l = 4

K_p = 12

K_l ≤ K ≤ K_p Rozkład reszt jest liniowy. Nie ma podstaw do odrzucenia hipotezy H₀.

Postać modelu została poprawnie dobrana.

TEST NA NORMALNOŚĆ ROZKŁADU SKŁADNIKA LOSOWEGO ZA POMOCĄ TESTU SHAPIRO-WILKA

Stawiam hipotezę:

H0: składnik losowy ma rozkład normalny

H1: składnik losowy nie ma rozkładu normalnego

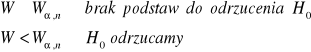
ei	et uporządkowane rosnąco	eN-i+1-ei	N-i+1	N-i+1(eN-i+1-ei)	(ei-^-e)^2
-2,44276552	-27,02242743	44,74204	0,5150	23,0421	5,967103
10,54539958	-18,43530536	33,56171	0,3306	11,0955	111,2055
1,007292505	-18,17135961	31,24525	0,2495	7,7957	1,014638
-3,685135039	-12,57048238	24,03584	0,1878	4,5139	13,58022
2,634228795	-6,220264133	15,44759	0,1353	2,0901	6,939161
-19,3505512	-5,808869804	12,93592	0,0880	1,1384	374,4438
-0,851205363	2,957814111	3,505526	0,0433	0,1518	0,724551
7,633243458	5,067912028	5,067912	0,0000	0,0000	58,26641
5,77914229	6,463340061				33,39849
4,635581959	7,127050855				21,48862
-0,120703519	9,22732908				0,014569
2,064367346	11,46535747				4,261613
-8,681048169	13,07389186				75,3606
-7,426454297	15,12640445				55,15222
8,258607181	17,7196088				68,20459
0,00			Σ	49,8275	830,0221

korzystam ze wzoru:

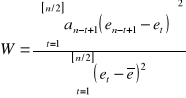
W=	2,991219057

Z tablic wartości krytycznych dla testu Shapiro - Wilka odczytuję wartość krytyczną dla a=0,05 i n=15:

Wa,n=	0,881
W > Wa,n - brak podstaw do odrzucenia H0

Składnik losowy ma rozkład normalny

BADAM HOMOSCEDASTYCZNOŚĆ SKŁADNIKA LOSOWEGO ZA POMOCĄ TESTU HARRISONA-MC CABE`A

H0: σ_t² = const

H1: σ_t² ≠ const

b < b_L => H₀ odrzucamy

b_L ≤ b ≤ b_U => brak decyzji

b > b_U => brak podstaw do odrzucenia H0

n	et	et uporządkowane rosnąco	et^2
1	-2,4427655	-19,3505512	374,4438319
2	10,5453996	-8,6810482	75,3605973
3	1,0072925	-7,4264543	55,1522234
4	-3,6851350	-3,6851350	13,5802203
5	2,6342288	-2,4427655	5,9671034
6	-19,3505512	-0,8512054	0,7245506
7	-0,8512054	-0,1207035	0,0145693
8	7,6332435	1,0072925	1,0146382
9	5,7791423	2,0643673	4,2616125
10	4,6355820	2,6342288	6,9391613
11	-0,1207035	4,6355820	21,4886201
12	2,0643673	5,7791423	33,3984856
13	-8,6810482	7,6332435	58,2664057
14	-7,4264543	8,2586072	68,2045926
15	8,2586072	10,5453996	111,2054522
∑			718,8166122

Statystyka Harrisona - Mc Cabe'a ma postać:

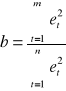
b= 0,730705283

Dla a=0,05 z tablic Fishera - Snedecora odczytuję wartość dla F1 i F2:

F1= 4,82

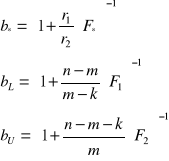
F2= 3,87

Obliczam wartości krytyczne korzystając ze wzoru:

b_L= 0,114784206

b_U= 0,231634679

b>b_u brak podstaw do odrzucenia Ho

ZA POMOCĄ TESTU DURBINA WATSONA BADAM AUTOKORELACJĘ SKŁADNIKA LOSOWEGO

Stawiam hipotezę:

H0: nie występuje autokorelacja określonego rzędu

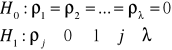
H1: występuje autokorelacja, ale nie jest określone jakiego rzędu

ei	ei - 1	ei - ei - 1	(ei - ei - 1 )^2	ei^2
-2,44276552	-	-	-	5,967103384
10,54539958	-2,44276552	12,98817	168,6924	111,2054522
1,007292505	10,54539958	-9,53811	90,97549	1,01463819
-3,685135039	1,007292505	-4,69243	22,01888	13,58022025
2,634228795	-3,685135039	6,319364	39,93436	6,939161343
-19,3505512	2,634228795	-21,9848	483,3306	374,4438319
-0,851205363	-19,3505512	18,49935	342,2258	0,72455057
7,633243458	-0,851205363	8,484449	71,98587	58,26640569
5,77914229	7,633243458	-1,8541	3,437691	33,39848561
4,635581959	5,77914229	-1,14356	1,30773	21,48862009
-0,120703519	4,635581959	-4,75629	22,62225	0,01456934
2,064367346	-0,120703519	2,185071	4,774535	4,261612537
-8,681048169	2,064367346	-10,7454	115,464	75,36059732
-7,426454297	-8,681048169	1,254594	1,574006	55,15222342
8,258607181	-7,426454297	15,68506	246,0212	68,20459257
		Σ	1614,365	830,0220644

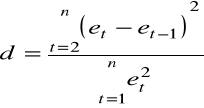
Statystyka Durbina Watsona ma postać:

d= 1,944966002

0≤1,944966002 ≤4

1,944966<2 : zakładamy, że istnieje autokorelacja dodatnia H1:p1>0

Z tablic wartości krytycznych statystyki Durbina-Watsona odczytuję d_u i d_l dla a=0,05, n=15, k=2

dl=0,95

du=1,54

Ponieważ d>du (1,944966>1,54) nie ma podstaw do odrzucenia hipotezy H0. Reszty nie są skorelowane, co świadczy o poprawności modelu.

PODSUMOWANIE

Model postaci:

Yi= 1367,24687-85,304676X2i-0,00737586X5i
	110,2432	11,3596		0,0004

Gdzie:

Y - liczba urodzeń [tyś.osób]
X2 - liczba kobiet w wieku rozrodczym [tyś.osób]
X5 - PKB na 1 mieszkańca w zł

Jest dopasowany do danych empirycznych w 98,83%.

Spełnia testy na liniowość, normalność składnika losowego, brak występowania autokorelacji składnika losowego oraz na stałość wariancji. Model jest homoscedastyczny.

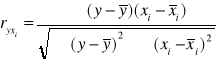
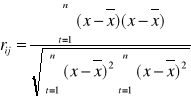
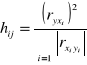
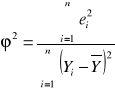
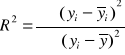
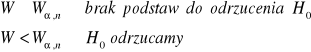
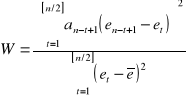
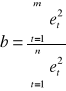
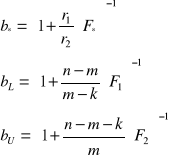
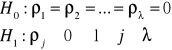
X1

X5

X3

X2

X4

---