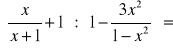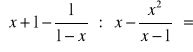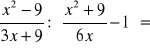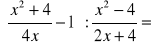Dana jest funkcja ![]()
. Wykaż, że dziedziną funkcji jest zbiór R.
Wyznacz dziedzinę:
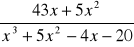
,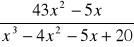
,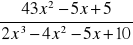
,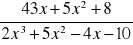
.
Rozszerz wyrażenie tak, aby otrzymać wyrażenie o wskazanym mianowniku: ![]()
. Wyznacz dziedziny lewej i prawej strony równości.
Skróć ułamek ![]()
i oblicz jego wartość dla ![]()
.
Wykonaj działania (pamiętaj o zastrzeżeniach):
Wykonaj działania (pamiętaj o zastrzeżeniach):
Wykonaj działania (pamiętaj o zastrzeżeniach):
Rozwiąż równania:
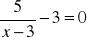
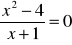
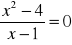
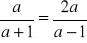
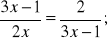
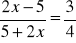
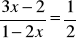
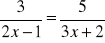
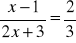
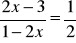
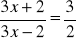
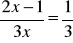
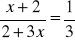
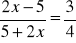
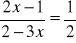
;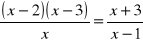
Rozwiąż równania:
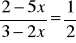
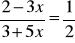
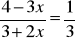
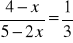
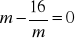
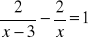
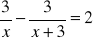
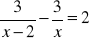
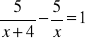
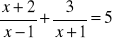
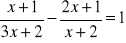
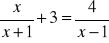
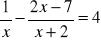
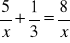
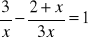
;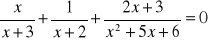
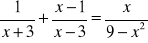
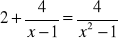
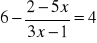
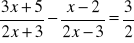
Rozwiąż nierówność
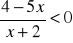
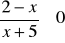
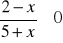
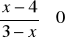
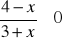
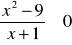
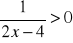
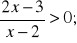
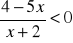
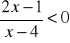
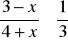
.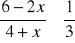
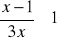
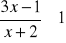
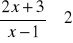
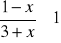
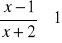
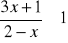
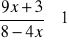
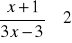
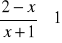
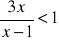
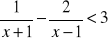
Rozwiąż nierówność
Wykonaj wykres funkcji, określ dziedzinę i zbiór wartości