Instytut Fizyki

Politechniki Warszawskiej

LABOLATORIUM FIZYKI

Ćwiczenie nr 12

Temat: Badanie procesów relaksacyjnych.

1. Opis ćwiczenia i opracowanie wyników.

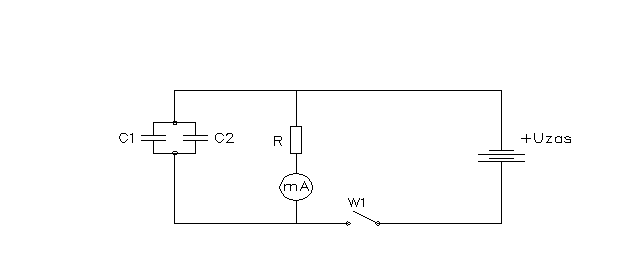
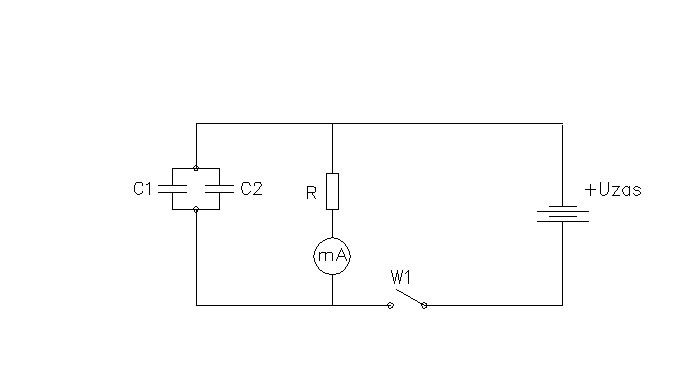
Badanie procesu ładowania kondensatora

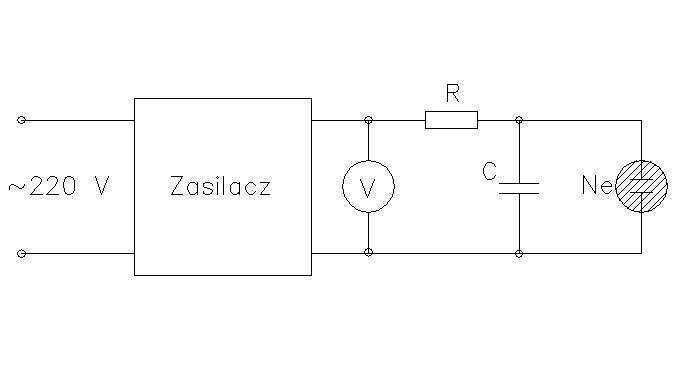
Schemat pomiarowy

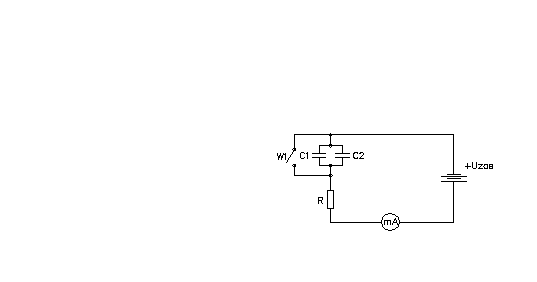
Wartości elementów
C1	88,5uF	±5%
C2	88,5uF	±5%
R1	220k	±5%
R2	296k	±1%

Pojemność wypadkowa połączenia równoległego kondensatorów

1. Pomiar czasu połowicznego zaniku prądu ładowania - T_1/2

- przy zwartym włączniku W1 (kondensator rozładowany), regulując napięcie zasilające, w obwodzie wymusiliśmy przepływ prądu
(z prawa Ohma łatwo więc można wyliczyć przybliżone napięcie zasilające układ
)

- po rozwarciu W1 mierzymy czas po którym prąd ładowania w obwodzie spadnie do wartości

Te same czynności powtarzamy dla rezystora R2 (przybliżone napięcie zasilające układ
)

wyniki pomiarów:

nr elem.	C(F)	R(k)	lp	1	2	3	T1/2śr[s]
1	177	220	T1/2[s]	21,71	21,73	21,71	21,72
2	177	296	T1/2[s]	29,28	29,32	29,3	29,30

Czasy relaksacji obwodów RC:

a) - liczony z zależności

- liczony teoretycznie ze wzoru:

- liczony z zależności

- liczony teoretycznie ze wzoru:

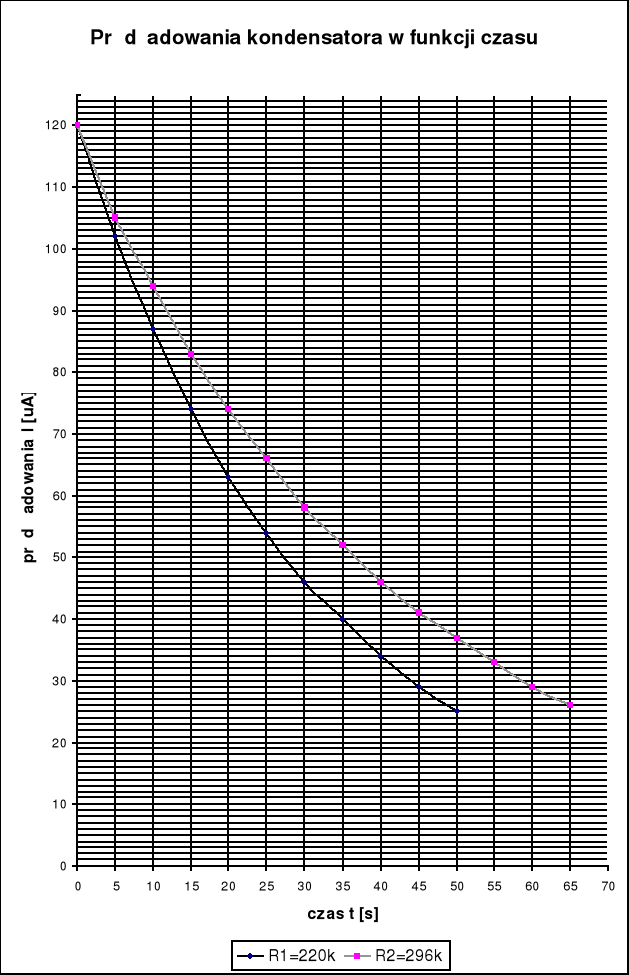
Następnie wykonujemy pomiary prądu ładowania kondensatora w funkcji czasu:

C(F)	R(k)	t[s]	0	5	10	15	20	25	30	35	40	45	50	55	60	65
177	220	J()	120	102	87	74	63	54	46	40	34	29	25	-	-	-
		296	J()	120	105	94	83	74	66	58	52	46	41	37	33	29	26

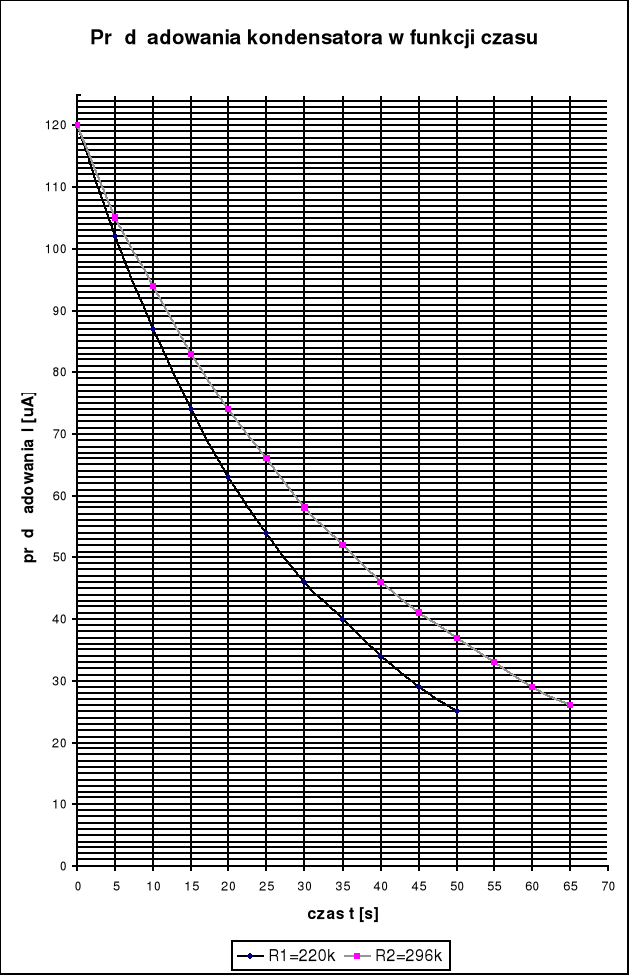
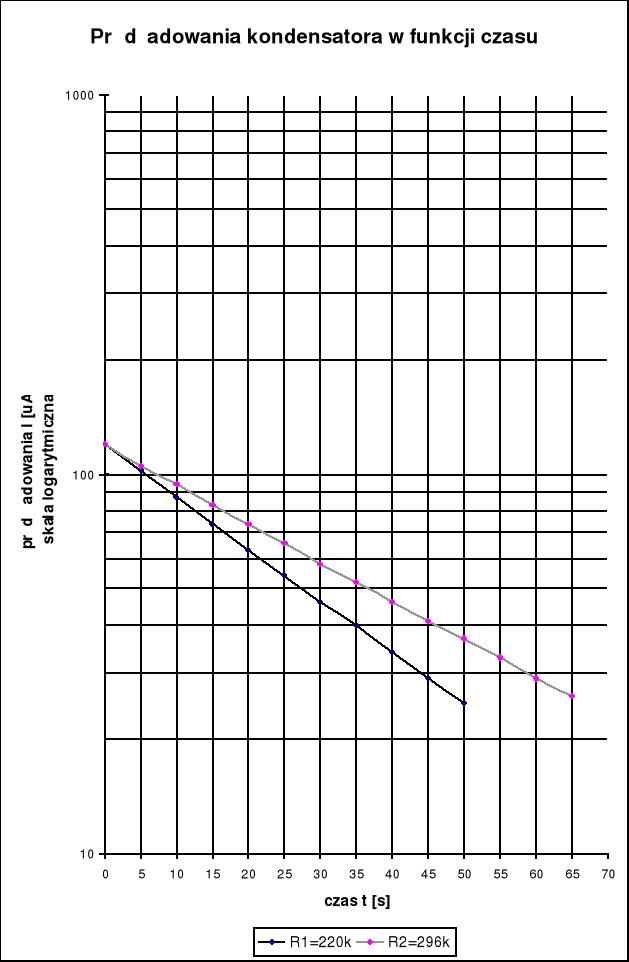
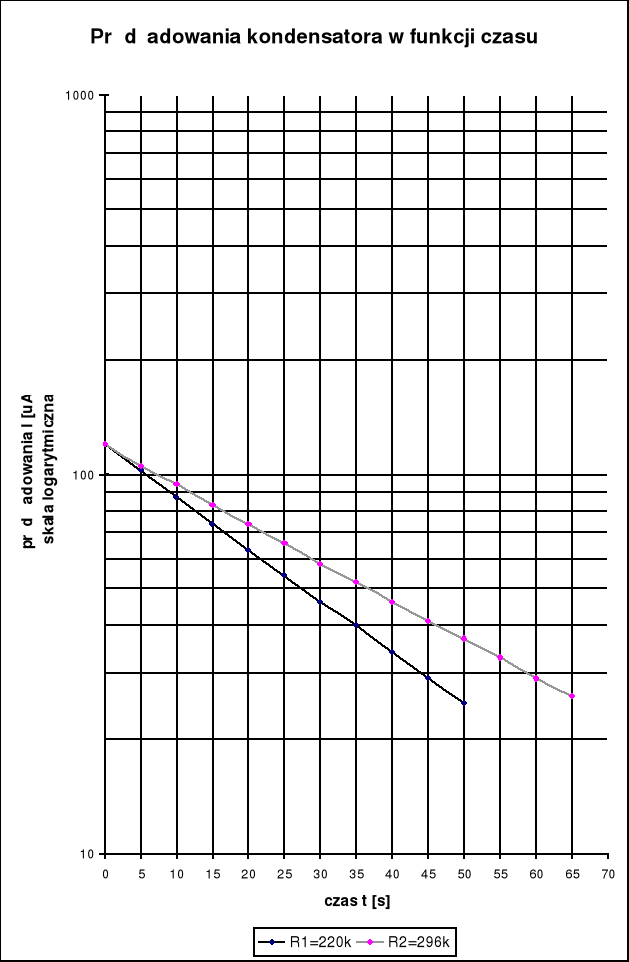
Obliczenie czasu relaksacji dla ładowania kondensatora metodą najmniejszej sumy kwadratów:

R1=220kΩ

C=177μF

Korzystając z tego wzoru mamy określić nachylenie wykresów

W tym układzie punkty pomiarowe układają się na wykresach wzdłuż linii prostych
, a więc obliczenie
sprowadza się do obliczenia odwrotności współczynnika kierunkowego prostej.

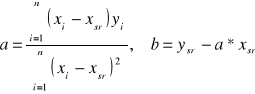
R1=220k, C=177uF
lp	x(t[s])	y[ln J]	x-xsr	(x-xsr)^2	(x-xsr)*y	[y-a(x-xsr)-ysr]^2
1	0	-9,02801882	-25	625	225,70	8,12492E-05
2	5	-9,19053774	-20	400	183,81	1,02245E-05
3	10	-9,34960244	-15	225	140,24	6,98176E-07
4	15	-9,51144546	-10	100	95,11	1,85311E-05
5	20	-9,67237583	-5	25	48,36	7,28029E-05
6	25	-9,82652651	0	0	0,00	3,57659E-05
7	30	-9,98686916	5	25	-49,93	9,25527E-05
8	35	-10,1266311	10	100	-101,27	5,35869E-05
9	40	-10,28915	15	225	-154,34	2,2622E-06
10	45	-10,4482147	20	400	-208,96	7,36082E-07
11	50	-10,5966347	25	625	-264,92	5,51265E-05
	xsr	ysr				
	2,50E+01	-9,82054605		2750	-8,62E+01	0,000423536

=31,91 [s]

Średnie błędy kwadratowe wyznaczenia współczynników a i b:

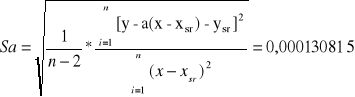
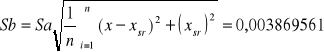
zakładam żądany poziom ufności
=0,95

poziom istotności
=1-
=0,05

k=n-r, gdzie n - liczba pomiarów, r - liczba parametrów

Ponieważ średnie błędy kwadratowe Sa iSb zostały wyznaczone na podstawie 2 równań wiążących to r=2, więc k=n-2.

W ćwiczeniu dokonano 11 pomiarów to k=9.

W tabelach statystycznych z rozkładem t-Studenta znajdujemy parametr t

lub
czyli t(0,05;9)=2,2622

*2,2622=0,0002959 [s]

*2,2622=0,0087537

Ostatecznie:

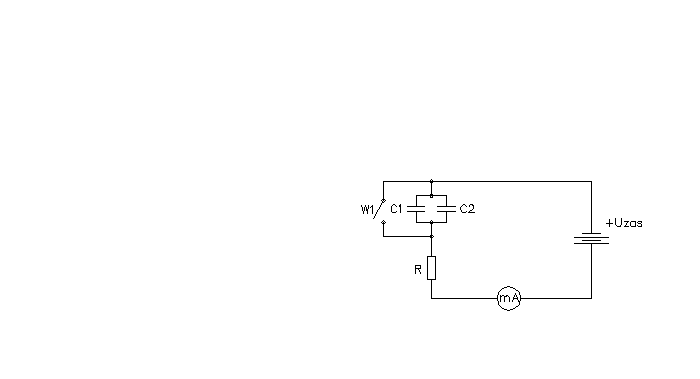
Badanie procesu rozładowania kondensatora

Schemat pomiarowy

Wartości elementów
C1	88,5uF	±5%
C2	88,5uF	±5%
R2	296k	±1%

Pojemność wypadkowa połączenia równoległego kondensatorów

1. Pomiar czasu połowicznego zaniku prądu rozładowania - T_1/2

- przy zwartym włączniku W1 (kondensator naładowany), regulując napięcie zasilające, w obwodzie wymusiliśmy przepływ prądu
(napięcie zasilające układ
)

- po rozwarciu W1 mierzymy czas po którym prąd rozładowania w obwodzie spadnie do wartości

wyniki pomiarów:

nr elem.	C[F]	R[k[	lp	1	2	3	T1/2śr[s]
2	177	296	T1/2[s]	28,82	28,79	28,81	28,81

Czasy relaksacji obwodów RC:

a) - liczony z zależności

- liczony teoretycznie ze wzoru:

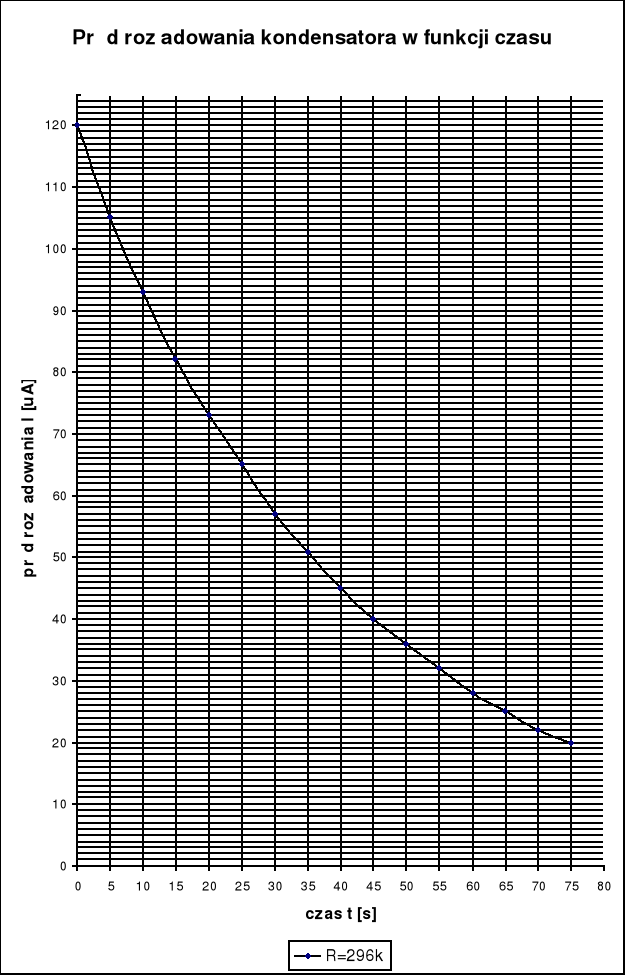
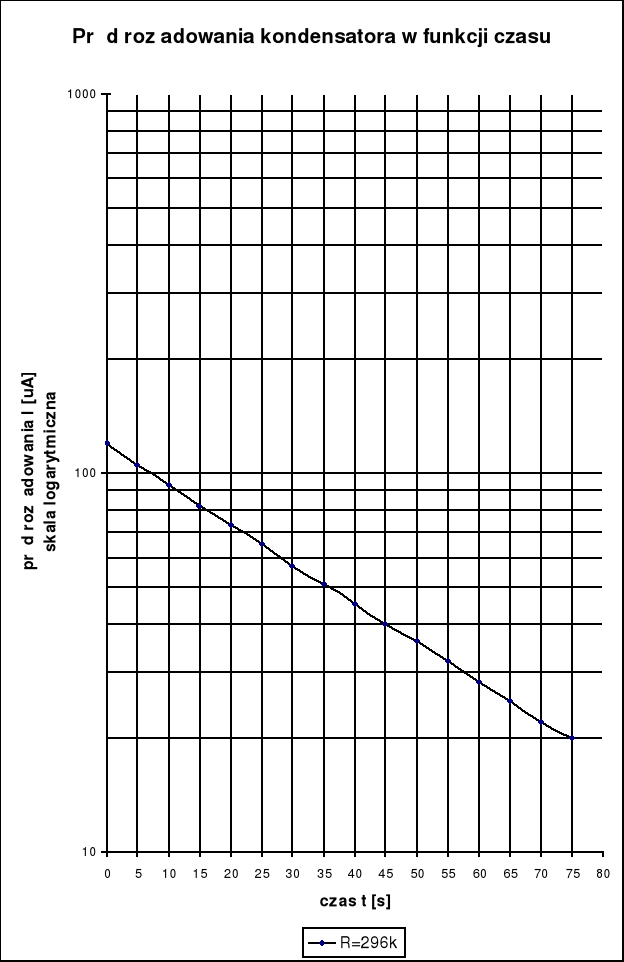
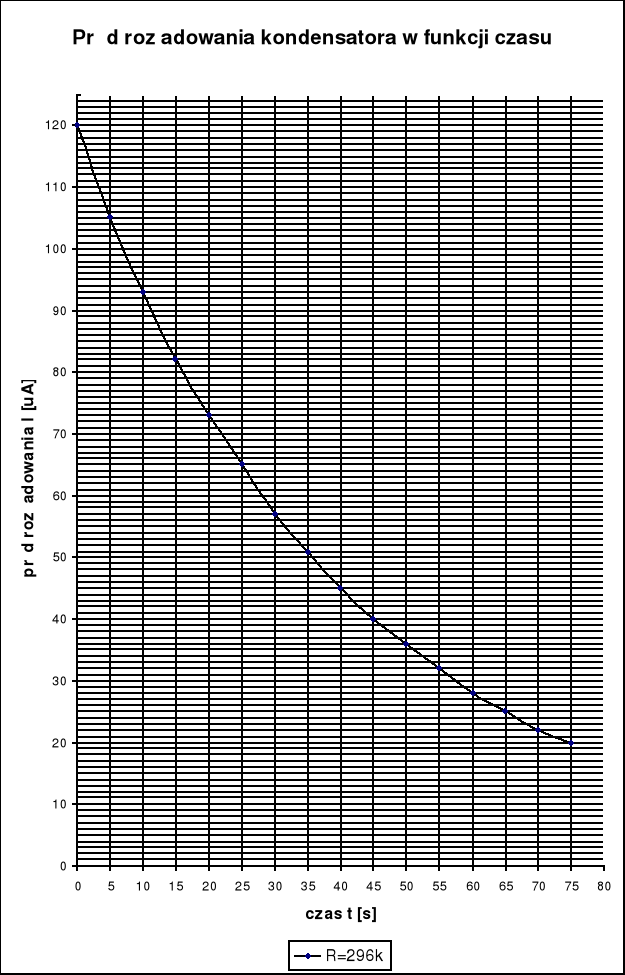
Następnie wykonujemy pomiary prądu rozładowania kondensatora w funkcji czasu:

C[F]	R[k	t[s]	0	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75
177	296	J[]	120	105	93	82	73	65	57	51	45	40	36	32	28	25	22	20

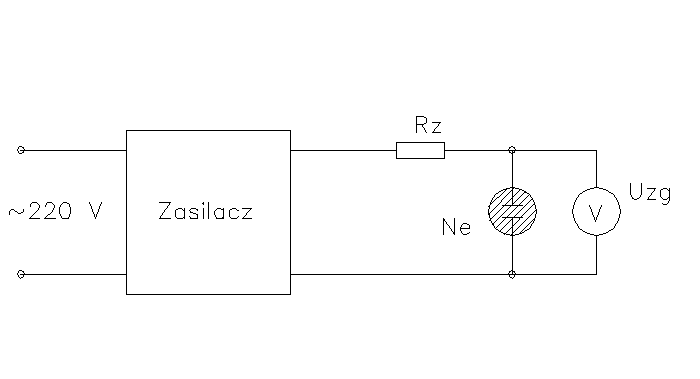
Badanie napięcia zapłonu Uz i gaśnięcia Ug neonówki

Schemat pomiarowy

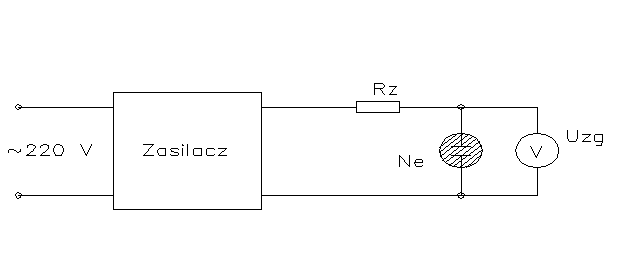
Wartości elementów
R	50k	±1%

Pomiar napięcia zapłonu polegał na zwiększaniu Uzaś od małych wartości i odczytaniu z woltomierza najwyższą wartość napięcia przed zaświeceniem neonówki (w momencie zaświecenia napięcie spada o kilkanaście woltów do tzw. napięcia pracy).

Natomiast napięcie gaszenia Ug polegało na zmniejszaniu napięcia aż do wygaszenia żarzenia gazu i zanotowaniu najmniejszej wartości przy którym neonówka gaśnie.

wyniki pomiarów:

n	1	2	3	4	5	6	Uśr[V]
U [V]
Uz	70	69,8	69,7	69,6	69,6	69,5	69,7
Ug	56,6	56,9	56,1	56,6	56,2	56,1	56,42

Badanie zależności drgań od wartości oporności R i pojemności C

Schemat pomiarowy

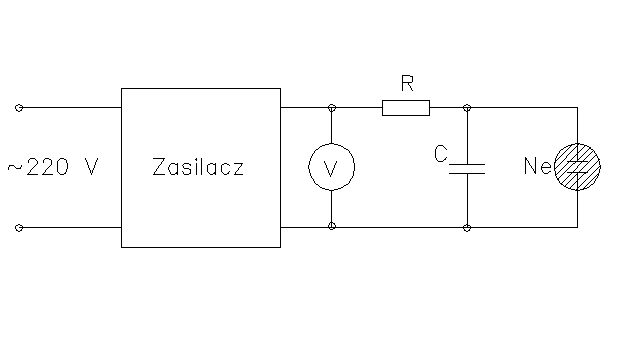
Po zmontowaniu układu pomiarowego według powyższego schematu ustawiamy wartość napięcia zasilacza Uzas tak, aby zaobserwować rozbłyski neonówki dla każdej wartości oporności R ( w naszym przypadku Uzas=80V i podczas pomiarów pozostawało stałe) i dokonujemy pomiaru czasu 20 rozbłysków neonówki.

wyniki pomiarów:

Uzas=80V
C(F)	R(k)	t20[s]	Teksp [s]
1	420	9	0,45
		470	9,1	0,455
		520	10	0,5
		550	10,7	0,535
		590	11,4	0,57
		680	12,2	0,61

Marcinowski Mariusz Gr.Z21 zespół III 05.01.2003

6

---