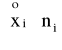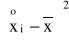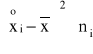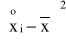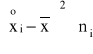Zadanie 1
W zakładzie X dla 16 wybranych losowo pracowników otrzymano następujące informacje o zatrudnionych:
Wiek pracowników |
20-24 |
24-28 |
28-32 |
32-36 |
Liczba pracowników |
4 |
6 |
4 |
2 |
Zakładając, że rozkład wieku jest normalny, wyznaczyć przedział ufności dla przeciętnego wieku pracowników tego zakładu, jeśli poziom ufności wynosi 0,98.
Traktując powyższe dane jako wyniki wstępnej próby obliczyć, jaka powinna być właściwa liczebność próby, aby oszacować przeciętny wiek pracownika z dopuszczalnym błędem oceny 2 lata - na poziomie ufności 0,98. Jaka powinna być liczebność próby, jeśli założymy dopuszczalny błąd oceny = 1 rok?
Jaki przedział otrzymamy zakładając, że wiek ma rozkład normalny pracowników N(m, 3) i poziom ufności wynosi 0,98?
Wyznaczyć przedział ufności dla odchylenia standardowego wieku pracowników na poziomie ufności 0,90 przy założeniu, że wiek ma rozkład N(m, σ).
(xi0, xi1> |
ni |
|
|
|
|
20-24 24-28 28-32 32-36 |
4 6 4 2 |
|
|
|
|
Σ |
16 |
X |
432 |
X |
240 |
a) X ~ N (m,σ) nie znamy σ
1 - α = 0,98
α = 0,02
n =16
Mamy przedział ufności dla średniej m w populacji WARIANT
![]()
![]()
![]()
![]()
![]()
![]()
α = 0,02 ν = n - 1 = 15
Odczytuję wartość z tablicy
![]()
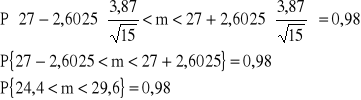
Z prawdopodobieństwem 0,98 przedział (24,4; 29,6) pokrywa nieznaną przeciętną wartość wieku zatrudnionych pracowników.
b)
1 - α = 0,98 Szukamy liczebność próby WARIANT
α = 0,02
d = 2 lata
no = 16 n małe
X ~ N (m,σ) nie znamy σ
![]()
![]()
![]()
![]()
![]()
n = 28
Właściwa liczebność próby powinna wynosić 28 pracowników, aby na poziomie ufności 0,98 oszacować przeciętny wiek pracownika z dopuszczalnym błędem oceny 2 lata. Należy, więc do 16 osobowej próby wstępnej dolosować 12 pracowników.
1 - α = 0,98
α = 0,02
d = 1 rok
nO = 16
![]()
![]()
![]()
n = 109
Należy wylosować minimum 109 pracowników, aby na poziomie ufności 0,98 oszacować przeciętny wiek pracownika, z maksymalnym błędem szacunku 1 rok. Należy, więc do 16 osobowej próby wstępnej dolosować 93 pracowników.
c)
n = 16 n małe
X ~ N(m,3) znamy σ (σ = 3)
1 - α = 0.98 zα = 2,33
α = 0,02
![]()
Mamy przedział ufności dla średniej m w populacji WARIANT
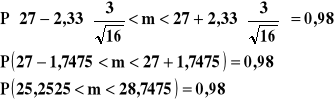
Z prawdopodobieństwem 0,98 przedział (25,2525;28,7475) pokrywa nieznaną przeciętną wartość wieku pracowników.
d) 1 - α = 0,90
X ~ N(m,σ)
n = 16 n małe
Przedział ufności dla wariancji σ2 w populacji WARIANT
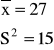
Odczytywanie: γ = n - 1 = 15
1 - α = 0,90
α = 0,10
![]()
![]()
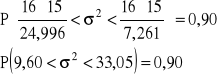
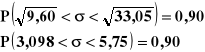
Z prawdopodobieństwem 0,90 przedział (3,098;5,75) pokrywa nieznaną wartość odchylenia standardowego wieku pracowników.
Zadanie 2
W 49-elementowej próbie losowej robotników otrzymano ![]()
jednorodnych operacji wykonanych w ciągu 1 dnia przy współczynniku zmienności 8%. Przyjmując poziom ufności 0,95 wyznaczyć metodą przedziałową przeciętną liczbę operacji w zbiorowości generalnej robotników.
![]()
1 - α = 0,95 zα = 1,96
n = 49
V=8%
![]()
![]()
![]()
S =9,6
n - duże
S - podane
σ - nieznane
Przedział ufności dla średniej m w populacji WARIANT
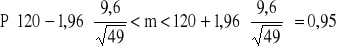
![]()
Z prawdopodobieństwem 0,95 przedział (117,31;122,69) pokrywa nieznaną przeciętną wartość liczby operacji w zbiorowości generalnej robotników.
Zadanie 3
Jaka powinna być minimalna liczebność próby, niezbędna do oszacowania odsetka uczniów zmierzających po maturze podjąć studia, jeśli w klasie liczącej 40 uczniów 70% zamierza kontynuować naukę w szkole wyższej (przyjąć poziom ufności 0,9 i maksymalny błąd szacunku 5%).
Jak zmieni się szacowana liczebność próby, jeśli w badanej klasie tylko 50% uczniów będzie miało w planie kontynuować naukę?
n = ? liczebność próby szukana
1 - α = 0,90
d = 5%= ![]()
n0 = 40
Przedział ufności dla wskaźnika struktury WARIANT
![]()
σ - nieznane
1 - α = 0,90 zα = 1,64
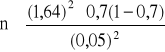
![]()
n = 226
Należy wylosować minimum 226 studentów, aby na poziomie ufności 0,90 oszacować procent studentów zmierzających po maturze podjąć studia z maksymalnym błędem szacunku 5%.
![]()
1 - α = 0,90 zα = 1,64
d = 0,05
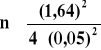
![]()
n = 269
Należy wylosować minimum 269 studentów, aby na poziomie ufności 0,90 oszacować procent studentów zmierzających po maturze podjąć studia z maksymalnym błędem szacunku 5%.
Zadanie 4
Dwunastu tokarzy wykonuje takie same części. Ich średnie wydajności w sztukach na godzinę wynoszą odpowiednio: 4,6; 6,1; 10,3; 9,8; 6,7; 12,3; 14,5; 8,7; 9,0; 7,3; 8,8; 11,2. Znaleźć realizację przedziału ufności dla wartości przeciętnej i wariancji liczby sztuk wykonywanych w ciągu godziny przez jednego tokarza na poziomie ufności 0,98.
a) n = 12 małe
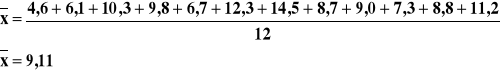
σ - nieznane
1 - α = 0,98 α = 0,02
Przedział ufności dla średnie m w populacji WARIANT
![]()
![]()
![]()
![]()
Odczytuję wartość z tablicy
![]()
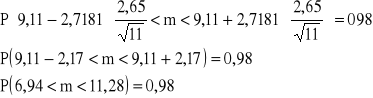
Z prawdopodobieństwem 0,98 przedział (6,94;11,28) pokrywa nieznaną przeciętną wartość liczby sztuk wykonywanych w ciągu 1 godziny przez jednego tokarza.
b) n = 12 n - małe
1 - α = 0,98
α = 0,02
Przedział ufności dla wariancji σ2 w populacji WARIANT
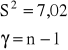
Odczytywanie:
![]()
![]()
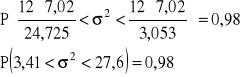
Z prawdopodobieństwem 0,98 przedział (3,41;27,6) pokrywa nieznaną wartość wariancji liczby sztuk wykonywanych w ciągu jednej godziny przez jednego tokarza.
Zadanie 5
Zapytano 200 losowo wybranych przedstawicieli rodzin, kto podejmuje poważniejsze decyzje finansowe? W 64% tych rodzin decyzje podejmuje małżonka. Jaki jest 99% przedział ufności dla odsetka rodzin, w których decyzje podejmuje małżonek?
n = 200 n - duże
1 - α = 99% 1 - α = 0,99 α = 0,01 zα = 2,58
Przedział ufności dla wskaźnika struktury
![]()
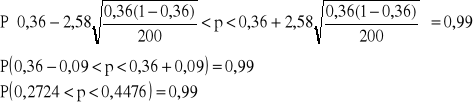
Z prawdopodobieństwem 0,99 przedział (0,2724;0,4476) pokrywa nieznaną wartość odsetka rodzin, w których decyzje podejmuje małżonek.
Zadanie 6
Notowano losowo czas poświęcony przez klientów banku na załatwienie formalności przy okienku kasowym i uzyskano następujące wyniki w minutach: 16, 18, 9, 11, 10, 13, 19, 18, 17, 15.
oszacować przeciętny czas przeznaczony przez klientów tego banku na załatwienie formalności w okienku kasowym (1-α= 0,95);
ocenić stopień zróżnicowania badanego czasu obsługi klientów;
traktując powyższą próbę jako wstępną, obliczyć, ile obserwacji czasu należałoby losowo przeprowadzić, aby oszacować przeciętny czas z wiarygodnością 0,90 (0,99) i maksymalnym błędem szacunku 2 minuty.
n = 10 n - małe
σ - nieznane
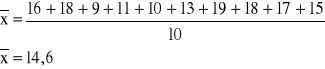
a) Przedział ufności dla średniej m w populacji WARIANT
![]()
![]()
![]()
![]()
1 - α = 0,95 α = 0,05 γ = n - 1 γ = 9
Odczytywanie:
![]()
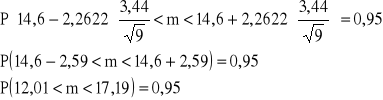
Z prawdopodobieństwem 0,95 przedział (12,01;17,19) pokrywa nieznaną przeciętną wartość czasu przeznaczonego przez klientów banku na załatwianie formalności w okienku bankowym.
b) oceń stopień zróżnicowania badanego czasu obsługi klientów.
Mamy przedział ufności dla wariancji σ2 w populacji
n = 10 n - małe
σ - nieznane ![]()
![]()
Odczytywanie:
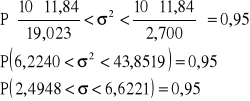
Z prawdopodobieństwem 0,95 przedział (2,4948; 6,6221) pokrywa nieznaną wartość odchylenia standardowego czasu obsługi klientów.
c)
no = 10
![]()
1 - α = 0,90 α = 0,10
d = 2 minuty
γ = n - 1
![]()
![]()
Odczytywanie:
![]()
![]()
![]()
n = 12
Należy wylosować minimum 12 klientów, aby na poziomie ufności 0,90 oszacować czas obsługi klientów z maksymalnym błędem szacunku 2 minuty. Należy, więc do 10 elementowej próby wstępnej dolosować 2 czasy.
no = 10
1 - α = 0,99 α = 0,01
d = 2
![]()
Odczytywanie:
![]()
![]()
![]()
n = 35
Należy wylosować 35 czasów, aby na poziomie ufności 0,99 oszacować przeciętny czas obsługi klientów z maksymalnym błędem szacunku 2 minuty. Należy, więc do 10 elementowej próby wstępnej dolosować 25 czasów.
Zadanie 7
Na egzaminie wstępnym na studia politechniczne stosowany jest niekiedy test spostrzegania kształtów. Dla wybranych w losowaniu niezależnych 200 kandydatów pewnej uczelni otrzymano następujące wyniki:
Wyniki testu (w pkt) |
5-9 |
10-14 |
15-19 |
20-24 |
25-29 |
30-34 |
35-39 |
40-44 |
Liczba osób |
2 |
16 |
25 |
50 |
50 |
40 |
15 |
2 |
Oszacować z wiarygodnością 0,99:
średni wynik testu spostrzegania kształtów wśród kandydatów tej uczelni,
stopień zróżnicowania wyników testu w tej zbiorowości.
a) 1 - α = 0,99 zα = 2,58
α = 0,01
n = 200 n - duże
σ - nieznane
<xio,xi1> |
ni |
|
|
|
|
5-9 |
2 |
7 |
14 |
324 |
648 |
10-14 |
16 |
12 |
192 |
169 |
2 704 |
15-19 |
25 |
17 |
425 |
64 |
1 600 |
20-24 |
50 |
22 |
1 100 |
9 |
450 |
25-29 |
50 |
27 |
1 350 |
4 |
200 |
30-34 |
40 |
32 |
1 280 |
49 |
1 960 |
35-39 |
15 |
37 |
555 |
144 |
2 160 |
40-44 |
2 |
42 |
84 |
289 |
578 |
Σ |
200 |
X |
5 000 |
X |
10 300 |
Przedział ufności dla średniej m w populacji WARIANT
![]()
![]()
![]()
![]()
![]()
S = 7,18
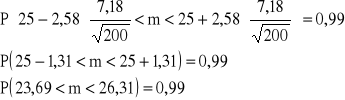
Z prawdopodobieństwem 0,99 przedział (23,69;26,31) pokrywa nieznaną przeciętną wartość punktów otrzymanych w teście na postrzeganie kształtów.
b) 1 - α = 0,99 zα = 2,58
α = 0,01
n = 200 n - duże
σ - nieznane
S = 7,18
Mamy przedział ufności dla wariancji σ2 w populacji
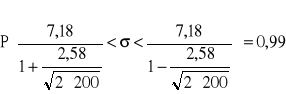
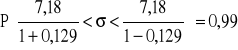
![]()
Z prawdopodobieństwem 0,99 przedział (6,3596; 8,2434) wyników testu spostrzegania kształtów.
Zadania dotyczące estymacji przedziałowej
8
B
INTERPRETACJA:
INTERPRETACJA:
INTERPRETACJA:
A
INTERPRETACJA:
A
INTERPRETACJA:
C
INTERPRETACJA:
3a
INTERPRETACJA:
INTERPRETACJA:
B
INTERPRETACJA:
A
INTERPRETACJA:
INTERPRETACJA:
B
INTERPRETACJA:
INTERPRETACJA:
INTERPRETACJA:
INTERPRETACJA:
C
INTERPRETACJA:
INTERPRETACJA:
B
Wyszukiwarka
Podobne podstrony:
Estymacja przedzialowa, Statystyka
03 Statystyka Matematyczna Estymacja przedziałowaid 4487
03 Statystyka Matematyczna Estymacja przedziałowa
Estymacja przedzialowa II, statystyka
materialy estymacja przedzialowa parametrow, AGH, Semestr VIII, Statystyka
Estymacja przedziałowa, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Statystyka mat mała próba rozwiązanie, Semestr II, Statystyka matematyczna
Zad do rozwiazania ST z PROB, Statystyka, Statystyka + Egzaminy, Statystyka + Egzaminy, Statystyka
Estymacja Przedzialowa cz 1
estymacja przedziałowa - wzory, Zad
6. Estymacja przedziałowa
MP 6 estymacja przedzialowa
Estymacja przedziałowa
rozwiazanie, Zadanie domowe statystyka
estymacja przedzialowa id 16372 Nieznany
więcej podobnych podstron