pochodne i zastosowania:
1. Wyznaczyć ekstrema funkcji:
a).![]()
b). ![]()
c). ![]()
odp. a). ![]()
b). ![]()
c). ![]()
2. Wyznaczyć ekstrema funkcji
a).![]()
b). ![]()
c). ![]()
odp.: a).y(0)=max; y(3)=ymin b). y(-1,5)=max c). ![]()
3. Napisać równanie stycznej w punkcie ![]()
do krzywej będącej wykresem funkcji:
![]()
odp.:y=2x+1
4. Napisać równanie stycznej w punkcie ![]()
do krzywej będącej wykresem funkcji:
![]()
odp. ![]()
czyli y=-4x+1
5. Wyznaczyć punkty przegięcia funkcji:
![]()
odp. W punkcie x=2/3 funkcja ma p. przegięcia (przechodzi z wklęsłej na wypukłą)
6. Wyznaczyć punkty przegięcia funkcji
![]()
odp.:W punkcie x=1 funkcja ma p. przegięcia , przechodzi z wypukłej na wklęsłą
7. Na podstawie wykresu wskazać zbiory argumentów, dla których funkcja jest rosnąca. W których punktach funkcja osiąga ekstrema? Przeanalizować znak pierwszej pochodnej tej funkcji dla x ze zbioru (2,10). Utworzyć tabelę zmienności tej funkcji.
8. Na podstawie wykresu wskazać zbiory argumentów, dla których funkcja jest
malejąca. W których punktach funkcja osiąga ekstrema? Przeanalizować znak drugiej pochodnej tej funkcji dla x ze zbioru (-2,2). Utworzyć tabelę zmienności tej funkcji.
9. Na podstawie wykresu wskazać zbiory argumentów, dla których funkcja jest
wklęsła. W których punktach funkcja osiąga ekstrema? Przeanalizować znak drugiej pochodnej tej funkcji dla x ze zbioru (4,6). Utworzyć tabelę zmienności tej funkcji.
10. Na podstawie wykresu wskazać zbiory argumentów, dla których funkcja jest
malejąca. W których punktach funkcja osiąga ekstrema? Przeanalizować znak drugiej pochodnej tej funkcji dla x ze zbioru (-2,2). Utworzyć tabelę zmienności tej funkcji.
11. Dla jakiej wartości parametru k układ równań ma jednoznaczne rozwiązanie. Znaleźć wartość współrzędnej x tego rozwiązania dla dowolnie ( ale odpowiednio) dobranej wartości parametru k.
a.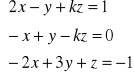
b.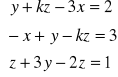
c.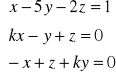
d.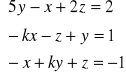
e.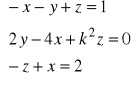
f.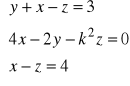
12. Dla jakiej wartości parametru a układ jest układem Cramera. Rozwiązać ten układ
a.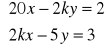
b.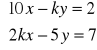
c.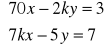
d.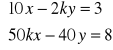
e.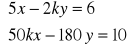
f.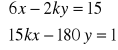
Odpowiedzido zad. 11, 12:
11.
a).
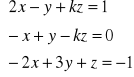
wyznacznik główny: 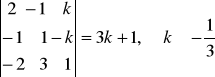
. Ustalając parametr k tak, aby był różny od (-1/3) możemy obliczyć wartości współrzędnych punktu, który jest rozwiązaniem danego układu równań. Każde z równań opisuje płaszczyznę w R3.
Np. niech k=1, wtedy 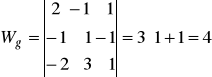
, 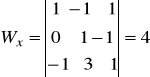
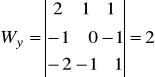
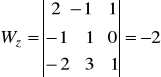
![]()
b).
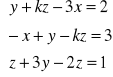
dany układ należy uporządkować: 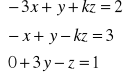
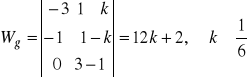
c).
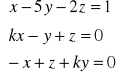
po uporządkowaniu układu otrzymujemy: 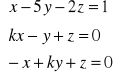
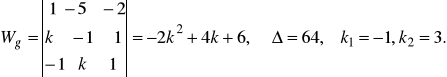
Żeby układ miał rozwiązanie ![]()
![]()
d).
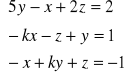
po uporządkowaniu układu otrzymujemy 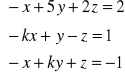
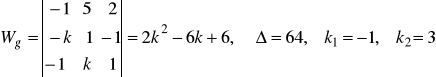
Żeby układ miał rozwiązanie ![]()
![]()
e).
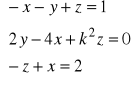
po uporządkowaniu układu otrzymujemy: 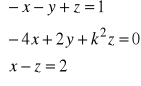
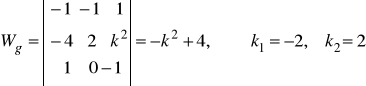
. Żeby układ miał rozwiązanie ![]()
![]()
f).
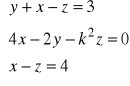
po uporządkowaniu układu otrzymujemy: 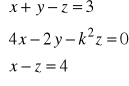
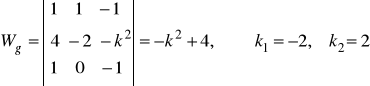
. Żeby układ miał rozwiązanie ![]()
![]()
12. Dla jakiej wartości parametru a układ jest układem Cramera. Rozwiązać ten układ
a).
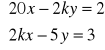
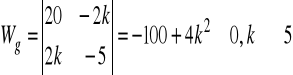
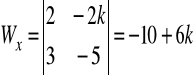
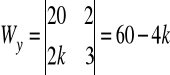
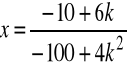
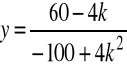
b).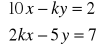
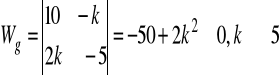
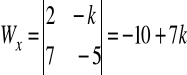
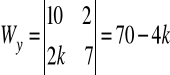
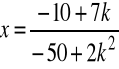
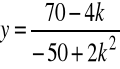
c).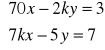
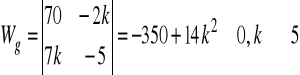
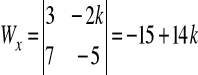
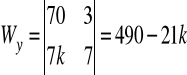
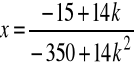
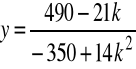
d).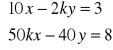
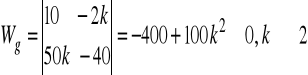
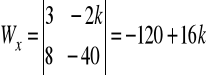
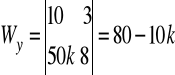
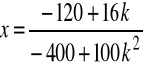
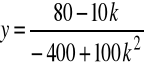
e).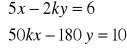
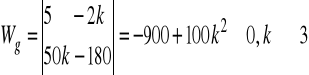
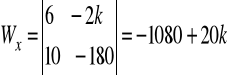
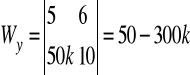
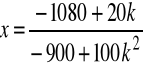
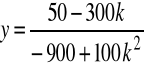
f).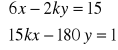
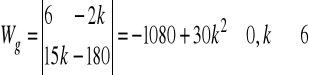
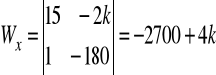
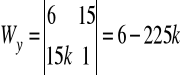
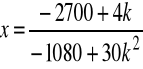
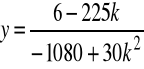
Wyszukiwarka
Podobne podstrony:
zjazd IV zad kol teoria studenci, leśnictwo, Sala tortur, 01.sem, mata
ekologia, leśnictwo, Sala tortur, ekologia
rozkłd jazdy - juwenalia 2010, Politechnika Lubelska, Studia, Studia, sem IV
510 Plan sesji egzaminacyjnej studia mgr sem II zjazd II 2010
BIOMATERIALY IV 2010
IV 2 Podstawy leśnictwa
zaliczenie farmacja 2010, far, II rok III sem, psychologia
parenteralne testy, Płyta farmacja Poznań, IV rok, technologia postaci leku 2, ćwiczenia, sem 2
Controlling Wyklad IV 2010
21.IV.2010, Meteorologia
Tematy energoelektronika 2010 na zaliczenie 30.01
Sp asp cz V 2010 Kom Sp 24 01 10
zagadnienia tpl- suche formy, Płyta farmacja Poznań, IV rok, technologia postaci leku 2, ćwiczenia,
writing syllabus first sem 2010-2011, Year 1, Writing WSz, I sem. Handouts + Syllabus
więcej podobnych podstron