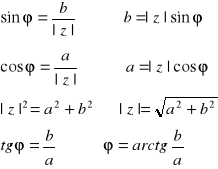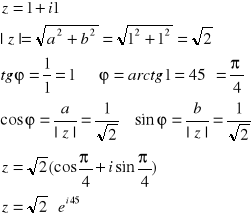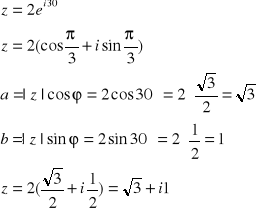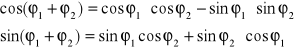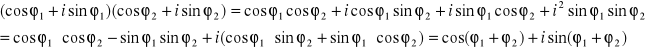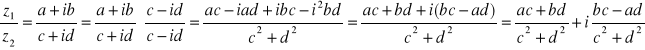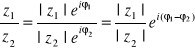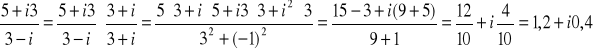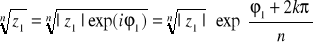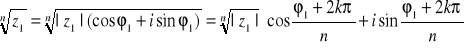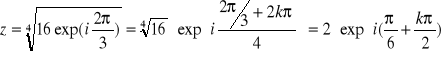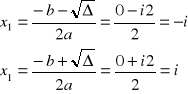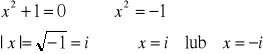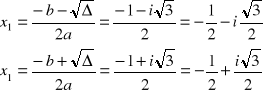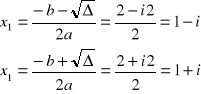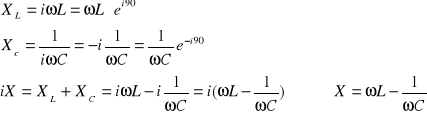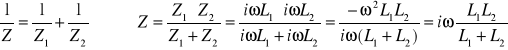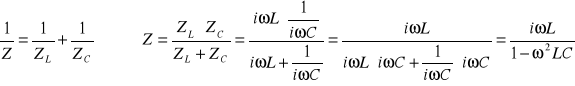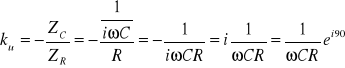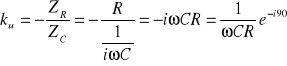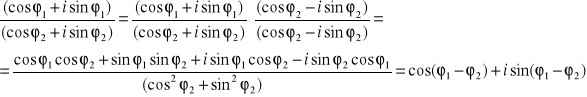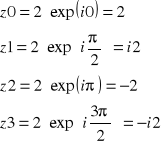Liczby zespolone

Liczby zespolone znalazły bardzo duże zastosowanie w matematyce, fizyce, mechanice, elektronice, automatyce. Służą do wyznaczania pierwiastków z liczb ujemnych, wyznaczania wszystkich pierwiastków równań wyższych rzędów (np. pierwiastki równania kwadratowego przy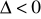
, dla liczb zespolonych każdy wielomian n-tego stopnia ma n pierwiastków), logarytmów z liczb ujemnych, kąta, gdy sinus lub cosinus ma wartość większą od 1 lub mniejszą od -1. W elektronice pozwala w bardzo łatwy sposób wyznaczać impedancję układów, które zawierają elementy rezystancyjne i reaktancyjne (takie jak indukcyjność, pojemność), liczyć przesunięcia fazowe wnoszone przez układ, wyznaczać transmitancję (jak układ przenosi sygnał z wejścia na wyjście, czy też inne wybrane miejsce). Stosowane są do wyznaczania stabilności układów tak elektronicznych jak i mechanicznych oraz wyznaczania innych wielu parametrów. Jakie są zalety ich stosowania? Upraszczają obliczenia i analizę.

Liczby zespolone są zbiorem liczb, do których należą też i liczby rzeczywiste, które są wszystkim dobrze znane. Czym się więc różnią? Oprócz części rzeczywistej (zwykłej liczby jaką znacie) posiadają też część urojoną. Dlatego też, liczbą zespoloną (jak sama nazwa wskazuje) nazywamy uporządkowaną parę liczb rzeczywistych (a,b). Ogólny symbol:

z = Re{z} + i Im{z}=a +ib;

gdzie: Re{z}=a - część rzeczywista liczby zespolonej x, (ang. real)

Im{z}=b - część urojona liczby zespolonej x (ang. imagine)

i - wyróżnia część urojoną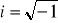
czyli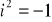

Często oznacza się liczbę zespoloną podkreśleniem z, a zamiast `i' może być `j'.

Liczby rzeczywiste są więc liczbami zespolonymi, których część urojona jest równa 0.

Np: 2 = 2 +i0; -4=-4+i0

Przykłady liczb zespolonych: 2+j3; 3; 1-j5 itp. - taką postać liczby zespolonej nazywamy kanoniczną.

Tak jak liczbę rzeczywistą przedstawia się na osi liczbowej, tak liczbę zespoloną jako, iż ma dwie składowe, możemy przedstawić na układzie współrzędnych, gdzie liczba z jest punktem na płaszczyźnie o współrzędnych (a,b). Na osi OX (x) przedstawia się część rzeczywistą (a), a na osi OY (y) część urojoną (b).

Skoro tak, to można też liczbę zespoloną przedstawić w innej postaci, zwanej wykładniczą, która będzie się składać z modułu |z|, który oznacza odległość punktu z od środka układu współrzędnych, oraz członu wykładniczego, który wskazuje kąt między osią OX i odcinkiem łączącym środek układu z punktem z, czyli modułem. Kąt liczony jest od osi OX do odcinka w kierunku przeciwnym do obrotu wskazówek

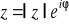
gdzie: |z| - moduł liczby z

φ - kąt, argument liczby z.

e - liczba niewymierna - liczba Nepera,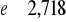

Ostatnią postacią jest postać trygonometryczna. Jak się dobrze przyjrzeć rysunkowi obok, to `a' i `b' można wyznaczyć znając moduł i argument liczby `z' - φ, korzystając z funkcji trygonometrycznej.

Tak dla przypomnienia:

Sinus danego kąta w trójkącie prostokątnym wyznaczany jest, jako stosunek przyprostokątnej naprzeciwległej do danego kąta do przeciwprostokątnej. Cosinus danego kąta w trójkącie prostokątnym wyznaczany jest, jako stosunek przyprostokątnej przyległej do danego kąta do przeciwprostokątnej. Tangens kąta to stosunek przyprostokątnych naprzeciwległej do przyległej do danego kąta.

arctg(A) -> funkcja, której wynikiem jest miara kąta, którego tg jest równy A.

Liczbę zespoloną można więc zapisać jako:

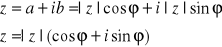
Tą postać nazywamy trygonometryczną.

Znając więc jedną postać łatwo jest wyznaczyć drugą postać:

Przykład 1: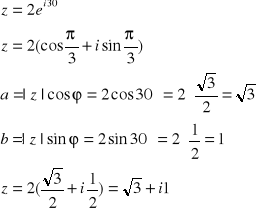

Przykład 2:

Przy zamianie z kanonicznej na wykładniczą lub trygonometryczną należy jednak pamiętać o jednym! Funkcje trygonometryczne posiadają po 2 rozwiązania w zakresie od 0 do 360 stopni, dlatego aby poprawnie wyznaczyć wartość kąta należy albo wyznaczyć sinus i cosinus oddzielnie ze wzorów (tak jak to zrobione w przykładzie) albo wyznaczyć kąt za pomocą jednej z tych funkcji najpierw sprawdzając w jakiej jest to ćwiartce.

Przykład: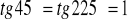
, ale jeżeli będzie 45 to wtedy liczba zespolona jest w pierwszej ćwiartce, `a' i `b' jest większe od zera, a jak 225 - `a' i `b' mniejsze od zera (III ćwiartka).

Z1=1+i1; Z2=-1-i1. dla obu z nich moduł jest równy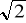
, a tangens równa się 1. Ale Z1 leży w pierwszej ćwiartce a Z2 w drugiej.

Po co to wszystko? Otóż każda z tych postaci ma swoje zalety. Postać kanoniczna wskazuje wprost wartość części rzeczywistej (np. rezystancję w układzie) i urojonej (np. reaktancję w układzie) i bardzo dobrze nadaje się do dodawania i odejmowania liczb zespolonych, a postać wykładnicza i trygonometryczna pozwala łatwo odczytać moduł i kąt przesunięcia i bardzo dobrze nadaje się do dzielenia, mnożenia, pierwiastkowania i potęgowania liczb zespolonych.

z1=a+ib

z2=c+id

Działania na liczbach zespolonych (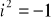
):

1) Liczba zespolona jest równa 0 gdy część rzeczywista i urojona jest równa 0, czyli a=0 i b=0 → 0=0+i0

2) Dwie liczby zespolone są sobie równe gdy ich części rzeczywiste i urojone są sobie równe tzn. a=c i b=d. W postaci wykładniczej gdy moduły są sobie równe a kąty mogą być równe lub przesunięte o wielokrotność 360°. Nie ma za to pojęcia mniejsza czy większa.

3) Moduł -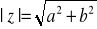
, argument -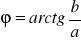

3) Liczba przeciwna: Liczba przeciwna do z1=a+ib to liczba -z1=-(a+ib) = -a-ib

Przykład: Liczba przeciwna do 2+i3 to -2-i3; liczba przeciwna do 4-i2 to -4+i2

4) Liczba sprzężona. Liczba sprzężona to liczba, której część urojona ma przeciwny znak, tzn. liczba sprzężona do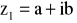
jest liczba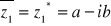
. Oznaczamy ja poprzez kręskę poziomą na górze lub poprzez symbol `*'

Przykład: Znajdź liczbę przeciwną do:

a) 3+i5 → 3-i5

b) 4-i3 → 4+i3

Właściwością liczby sprzężonej jest to, że: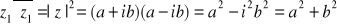

Wykorzystujemy to np. gdy chcemy pozbyć się liczby zespolonej z mianownika mnożąc go i licznik przez liczbę sprzężoną, lub też gdy dzielimy przez liczbę zespoloną.

5) Dodawanie liczb zespolonych - dodaje się oddzielnie części rzeczywiste i urojone:

z1+z2 = a + ib + c + id = a+c + i(b+d)

Przykład: Dodaj dwie liczby:

a) 2+i4 oraz 3+i → (2+i4)+(3+i) = 2+3 + i(4+1) = 5+i5

b) 3+i5 oraz 4-i2 → (3+i5)+(4-i2) = 3+4 + i(5-2) = 7+i3

6) Odejmowanie - odejmujemy oddzielnie części rzeczywiste od urojonych:

z1-z2 = (a+ib) - (c+id) = a-c + i(b-d)

Przykład: z1= 3+i4; z2=2-i; odejmij:

a) z1-z2 → (3+i4) - (2-i) = (3-2) + i(4-(-1)) = 1+i5

b) z2-z1 → (2-i) - (3+i4) = (2-3) + i(-1-4) = -1 -i5

7) Mnożenie - w postaci kanonicznej mnoży się wszystkie części przez siebie:

Przykład: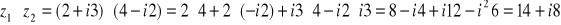

Mnożenie liczb w postaci wykładniczej lub trygonometrycznej jest łatwiejsze, korzysta się z zasady dodawania potęg przy mnożeniu liczb o tej samej podstawie lub z własności funkcji trygonometrycznych :

Jeżeli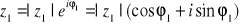
, a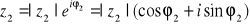
, to:

Otrzymuje się to wymnażając nawiasy i korzystając ze wzorów trygonometrycznych, które łatwo odnaleźć w tablicach matematycznych: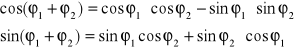

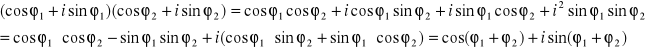
Przykład: Pomnóż dwie liczby:

a)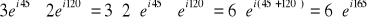

b)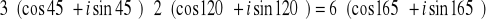

8) Dzielenie - w postaci kanonicznej wymnaża się przez liczbę sprzężoną do liczby przez którą się dzieli, dzielnik i dzielną. W postaci wykładniczej korzysta się z zasady odejmowania potęg przy dzieleniu liczb o tej samej podstawie, a w postaci trygonometrycznej ze wzorów trygonometrycznych.

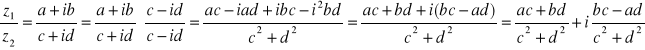
gdzie: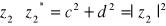
- czyli jest to moduł drugiej liczby.

W postaci wykładniczej, jeżeli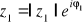
, a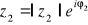
, to:

W postaci trygonometrycznej, jeżeli
,

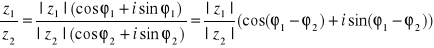
; otrzymuje się to z:

Korzysta się z jedynki trygonometrycznej: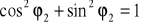
i wzorów na cosinus i sinus różnicy kątów (tablice matematyczne - podobne do sumy, różnica we znakach)

Przykład: Oblicz:

a)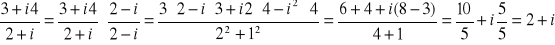

b)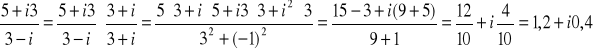

c)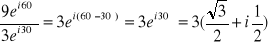

d)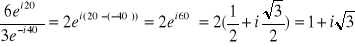

e)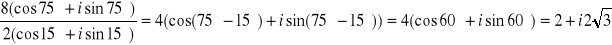

9) Potęgowanie - w postaci kanonicznej jest to bardzo pracochłonne, wymnaża się poszczególne nawiasy lub korzysta się z dwumianu Newtona. Bardzo proste jest to w postaci wykładniczej, gdzie korzysta się z zasady potęgowania potęg, czyli ich wymnożenia, lub trygonometrycznej, gdzie zwielokrotnia się kąt.

Przykład: Oblicz:

a)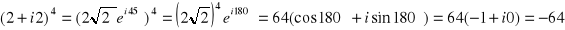

b)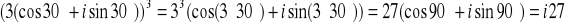

10) Pierwiastkowanie - podobnie jak potęgowanie tak i pierwiastkowanie wykonuje się na postaci wykładniczej lub trygonometrycznej.

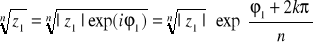
gdzie: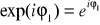

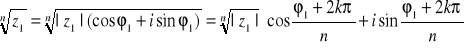
; dla k=0,1,….,n-1

Powoduje to, że dla każdej liczby zespolonej mamy tyle różnych pierwiastków ile wynosi stopień pierwiastka, tzn. jeśli mam pierwiastek 3 stopnia to mam 3 rozwiązania, które graficznie można przedstawić jako 3 punkty na okręgu o promieniu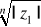
przesunięte względem siebie o 120 stopni czyli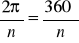
. Dzięki temu, można wyznaczyć tylko jeden z nich a resztę uzyskać poprzez podział okręgu co dane przesunięcie, czyli na n równych części. Przykład: Oblicz pierwiastek liczby:

a)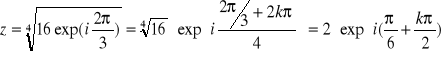

Otrzymujemy więc następujące rozwiązania:

- k=0;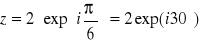

- k=1;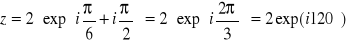

- k=2;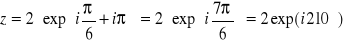

- k=3;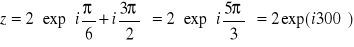

Gdyby te liczby podnieść do potęgi 4 otrzyma się liczbę pierwiastkowaną.

b)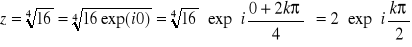

Jak widać pierwiastek czwartego stopnia z liczby rzeczywistej 16 ma w dziedzinie liczb zespolonych 4 rozwiązania. Tylko dwa z nich są czysto rzeczywiste i są powszechnie znane, a więc 2 i -2, które podniesione do potęgi 4 dają 16. Ale jeśli i2 i -i2 zostanie podniesione do potęgi 4 też otrzyma się 16, np.: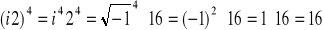

c)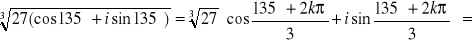

;

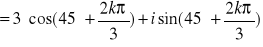
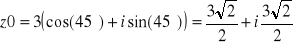
Właściwości niektórych liczb zespolonych

Liczba czysto rzeczywista:

- dodatnia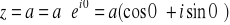
- leży na dodatniej części osi OX , nie przesuwa fazy

- ujemna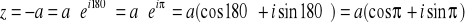
- leży na ujemnej części osi OX, odwraca fazę o 180°

Liczba czysto urojona:

- dodatnia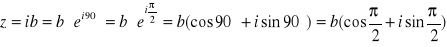
- leży na dodatniej części osi OY, przesuwa fazę o 90°

- ujemna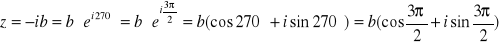
- leży na ujemnej części osi OY, przesuwa o 270°=-90° - opóźnia o 90°

Można też stosować miarę kąta ujemnego, tzn. liczonego zgodnie z obrotem wskazówek zegara wtedy dla kąta α wyznacza się go jako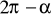
lub w mierze stopniowej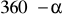
.

Skoro tak, to zamiast 270°można napisać -90°albo zamiast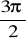
napisać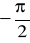
.

Odwrotność liczby czysto urojonej:

Zastosowanie liczb zespolonych

Zad1 Rozwiąż równanie kwadratowe:

a)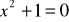
→

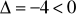
Skoro tak w dziedzinie liczb R nie ma rozwiązania ale…

W dziedzinie liczb zespolonych ma 2. Są to liczby sprzężone do siebie.

Inny sposób rozwiązania:

b)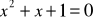

c)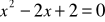

Liczby zespolone mają też bardzo duże zastosowanie w obliczaniu układów elektronicznych. Impedancja układów przy wymuszeniu sinusoidalnym może być przedstawiona w postaci zespolonej: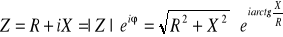

Gdzie: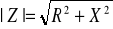
- moduł impedancji;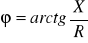
- przesunięcie fazowe,

część rzeczywista jest rezystancją (straty) a część urojona reaktancją (gromadzi energię).

Reaktancję wyznacza się jako sumę reaktancji cewki i kondensatora:

Korzystając z prawa Ohma :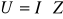

Otrzymujemy dla cewki: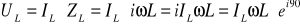

Z tego zapisu widać, że napięcie na cewce jest o +90° przesunięte względem prądu, czyli wyprzedza go o 90°. Jeżeli prąd ma charakter czysto rzeczywisty to napięcie czysto urojony.

Dla kondensatora: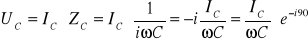

Napięcie jest przesunięte względem prądu w fazie o -90°, a więc jest opóźnione o 90°.

Jaka jest tego zaleta? Teraz wszystkie te elementy możemy traktować przy obliczeniach dla połączenia szeregowego, równoległego lub mieszanego tak jak rezystory podstawiając zamiast rezystancję ich impedancję, czyli rezystancję dla rezystorów i reaktancję przy cewkach i pojemności. Pozwala to w szybki sposób wyznaczyć przesunięcie fazowe jakie wnosi układ, jego zastępczą impedancję, bez rysowania wykresów wskazowych. Jeżeli mamy 2 cewki połączone równolegle to żeby policzyć ich zastępczą impedancję wystarczy skorzystać ze wzoru na rezystancję zastępczą dla połączenia równoległego zastępując R impedancją (reaktancją) cewki:

Jak widać takie połączenie zachowuje charakter indukcyjny (liczba dodatnia czysto urojona)

Przy połączeniu równoległym cewki i kondensatora:

Można zobaczyć, że zastępcza impedancja ma charakter indukcyjny (urojona dodatnia) gdy
, a charakter pojemnościowy (urojona ujemna) gdy
. Dla
- w działaniu występuje dzielenie przez 0, wtedy występuje rezonans.

Przy wykorzystaniu liczb zespolonych i obliczaniu zastępczej impedancji obwodów mieszanych można łatwo wyznaczać częstotliwości rezonansu czy to szeregowego (X=0 - część urojona równa się 0) czy równoległego (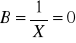
).

Liczby zespolone możemy też używać do wyznaczania transmitancji, a więc informacji o tym jak sygnał jest przenoszony w układzie z jednego miejsca w drugie. Przykładem tego może być wzmocnienie napięciowe. Taki zapis pozwala szybko określić nam przesunięcie fazowe układu, czyli o ile i jak przesunięty jest sygnał w fazie.

Na początek wzmacniacz odwracający:

Z tego zapisu widać, iż sygnał będzie wzmocniony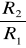
razy i przesunięty w fazie o 180°.

We wzmacniaczu całkującym na pierwszy rzut oka ciężko jest określić czy przesuwa o 180°, o 90° czy o -90°. Ale po dokonaniu zapisu w postaci liczb zespolonych, wszystko widać:

Podobnie jest ze wzmacniaczem różniczkującym:

Z tych wzorów jasno wynika, że wzmacniacz całkujący przesuwa o +90° a różniczkujący o -90°.

Przedstawianie sygnałów sinusoidalnych w postaci zespolonej:

Z postaci trygonometrycznej liczb zespolonych mamy:

Łatwo więc zauważyć, że: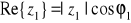
; załóżmy, że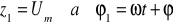

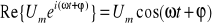
- jest więc to zwykły sygnał w czasie

W działaniach na liczbach zespolonych korzystamy jedynie z

, a więc mamy jedynie informacje o amplitudzie i fazie, a nie o pulsacji. Przeważnie korzysta się z wartości skutecznej sygnału tzn.
,

Przykłady:

a)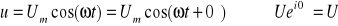

b)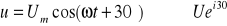

c)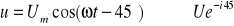

d)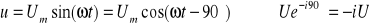

e)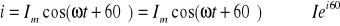

W obliczeniach na liczbach zespolonych, sygnały te zastępuje się danymi wyrażeniami.

Koniec

1

Re{z}

Im{z}

b

a

z=a+ib

φ

b

a

|z|

φ

z3

Re z

z0

z1

z2

z=a+ib

a

b

Im{z}

Re{z}

Im z

φ

Z

R

---