PRZYSPIESZENIE, podstawowa wektorowa wielkość fiz. charakteryzująca ruch; przyspieszenie opisuje szybkość zmian wektora prędkości ciała: przyspieszenie liniowe
— wektora prędkości liniowej
, przyspieszenie kątowe
— wektora prędkości kątowej. Przyspieszenie liniowe jest równe pochodnej prędkości liniowej względem czasu

a przyspieszenie kątowe — takiej samej pochodnej prędkości kątowej:

(często wystarczy posługiwać się wartościami średnimi

_średnie = Δ
 /Δt,
_średnie = Δ
 /Δt

Rzuty przyspieszenia liniowego na styczną i normalną do toru noszą odpowiednio nazwy przyspieszenia stycznego
_t (charakteryzuje zmianę wartości prędkości) i przyspieszenia normalnego
_r (dośrodkowego; charakteryzuje zmianę kierunku prędkości). Jednostkami przyspieszenia są: przyspieszenia liniowego — m/s², przyspieszenia kątowego — rad/s², stopień/s² i in.

PRĘDKOŚĆ, podstawowa, wektorowa wielkość fiz. charakteryzująca ruch. Przy opisie ruchu postępowego wprowadza się pojęcie prędkości liniowej
, prędkość liniowa jest równa pochodnej wektora położenia
względem czasu t:

a jej wartość v — pochodnej drogi s względem czasu:

w ruchu jednostajnym v równa się stosunkowi drogi s do czasu, w którym ta droga została przebyta: v = s/t; prędkość liniowa jest styczna do toru; jednostki prędkości liniowej: m/s, km/h. Ruch obrotowy charakteryzuje prędkość kątowa
; wektor prędkości kątowej jest skierowany wzdłuż osi obrotu i zwrócony w stronę, z której obrót ciała widać jako przeciwny do ruchu wskazówek zegara; wartość prędkości kątowej jest równa pochodnej kąta obrotu względem czasu t:

jednostki prędkości kątowej: rad/s, stop/s i in. Między prędkością liniową punktu ciała a jego prędkością kątową w ruchu obrotowym zachodzi związek

— wektor położenia punktu

PĘD,
, jedna z podstawowych wielkości fiz. charakteryzujących ruch układu; pęd punktu materialnego o masie m i prędkości
równy jest

pęd układu mech. jest sumą wektorową pędów poszczególnych punktów układu lub iloczynem całkowitej masy M układu i prędkości
jego środka masy.

Pęd spełnia zasadę zachowania: pędu odosobnionego (izolowanego) układu mech., tj. nie poddanego oddziaływaniom zewn., pozostaje wielkością stałą. Siły wewn. nie mogą zmieniać całkowitego pędu układu, choć pędy poszczególnych ciał mogą ulegać zmianie (zasada zachowania pędu tłumaczy m.in. zjawisko odrzutu przy wystrzale).

Zmiana pędu może zachodzić jedynie w wyniku oddziaływań zewn.; zmianę tę wyraża zależność

gdzie
— wypadkowa sił zewn., t — czas jej działania. Pęd mają wszystkie formy materii, także pole grawitacyjne i eletromagnet.

MOMENT PĘDU, kręt, wielkość charakteryzująca ruch ciała (układu materialnego), zwł. ruch obrotowy. Moment pędu
punktu materialnego P o pędzie
względem punktu 0 jest określony iloczynem wektorowym

gdzie
— promień wodzący poprowadzony od punktu 0 do P. Moment pędu bryły sztywnej względem osi, wokół której obraca się z prędkością kątową
, wyraża się wzorem

gdzie I — moment bezwładności bryły względem tej osi. Moment pędu spełnia zasadę zachowania: moment pędu zamkniętego układu mech., tj. takiego, na który nie działają siły zewn., pozostaje wielkością stałą; siły wewn. nie mogą zmienić całkowitego momentu pędu układu, choć momenty pędu poszczególnych ciał układu mogą ulec zmianie. Zmianę momentu pędu wywołuje działanie na ciało momentu siły
; zgodnie z drugą zasadą dynamiki ruchu obrotowego:

RUCH, fiz. zmiana w czasie położenia ciała materialnego względem wyróżnionego układu odniesienia, zmiana wzajemnego położenia elementów ciała, a także rozchodzenie się zaburzeń pól fizycznych

NEWTONA ZASADY DYNAMIKI, 3 podstawowe prawa dynamiki. I zasada dynamiki Newtona, zw. też zasadą bezwładności : jeśli na ciało nie działają żadne siły lub jeśli działające siły wzajemnie się równoważą, to istnieje układ odniesienia, w którym ciało spoczywa lub porusza się ruchem jednostajnie prostoliniowym;

II zasada dynamiki Newtona: zmiana pędu ciała jest proporcjonalna do przyłożonej siły

w mechanice nierelatywistycznej równanie to sprowadza się do postaci

m — masa ciała,
— jego prędkość,
— przyspieszenie,
— siła działająca, t — czas); dla ruchu obrotowego II zasada dynamiki przyjmuje postać:

gdzie I — moment bezwładności ciała,
— przyspieszenie kątowe, M — moment siły

III zasada dynamiki Newtona, zw. prawem akcji i reakcji (słuszna tylko w mechanice nierelatywistycznej): każdemu działaniu towarzyszy równe mu, skierowane przeciwnie — przeciwdziałanie. Zasady dynamiki Newtona są spełnione w inercjalnych układach odniesienia; w układach nieinercjalnych są słuszne dopiero po uwzględnieniu — oprócz sił rzeczywistych — fikcyjnych → sił bezwładności

INERCJALNY UKŁAD, układ odniesienia, w którym jest spełniona zasada bezwładności , czyli taki, w którym ciała nie podlegające działaniu żadnych sił lub podlegające działaniu sił o wypadkowej równej zeru spoczywają lub poruszają się ruchem jednostajnym prostoliniowym. W nieinercjalnych układach odniesienia prawa dynamiki są słuszne dopiero po dołączeniu do sił rzeczywistych sił pozornych -sił bezwładności.

SIŁA BEZWŁADNOŚCI, siła pozorna, siła występująca w nieinercjalnym układzie odniesienia, nie związana z oddziaływaniem żadnych konkretnych ciał; przykładami sił bezwładności są: siła Coriolisa i siła odśrodkowa. Równanie ruchu punktu materialnego w nieinercjalnym układzie odniesienia pod wpływem wypadkowej sił rzeczywistych i sił bezwładności ma taką samą postać, jak równanie ruchu tego punktu w układzie inercjalnym pod wpływem sił rzeczywistych; siłę bezwładności działającą na punkt materialny można wyrazić wzorem:

gdzie m — masa punktu materialnego,
_u — przyspieszenie unoszenia,
_c — przyspieszenie Coriolisa.

SIŁA CORIOLISA, jedna z sił bezwładności, której dodanie do sił faktycznie działających na ciało uwzględnia wpływ ruchu obrotowego nieinercjalnego układu odniesienia U' na ruch ciała w tym układzie; siła Coriolisa jest równa

gdzie m — masa ciała,
_c — przyspieszenie Coriolisa, które jest równe iloczynowi wektorowemu podwojonej prędkości kątowej układu U' względem inercjalnego układu odniesienia U i prędkości ciała
` względem U' : a_c = 2
×
'; siła Coriolisa ma zatem kierunek prostop. zarówno do
jak i do
'. Na ciała poruszające się w pobliżu pow. Ziemi działa siła Coriolisa wywołana ruchem obrotowym Ziemi. Siła Coriolisa wywołuje szereg zjawisk, m.in. powoduje, że ciała spadające pionowo odchylają się (w przybliżeniu) na wschód, natomiast ciała poruszające się na pow. Ziemi odchylają się: na półkuli pn. w prawo, a na półkuli pd. w lewo względem kierunku ruchu; prowadzi to m.in. do silniejszego podmywania odpowiednich brzegów oraz niektórych prądów morskich i powietrznych.

PRACA, W, skalarna wielkość fiz. określająca wartość energii wydatkowanej na przemieszczenie ciała materialnego z jednego położenia do drugiego. Praca wykonywana przez siłę
działającą na ciało przemieszczające się od punktu A do B jest równa

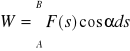
gdzie d
— wektorowy element drogi; jeśli
 = const, a ciało porusza się ruchem prostoliniowym, to

W = Fs cosα

gdzie α — kąt między kierunkiem siły i drogi.

Pracę wykonaną przez prąd elektr. określa prawo Joule'a-Lenza, które w ogólnym sformułowaniu ma postać

gdzie
— wektor gęstości prądu elektr.,
— wektor natężenia pola elektr., a całkowanie odbywa się po objętości przewodnika V i czasie t; dla prostszego przypadku stałego prądu elektr. W = U I t (U — napięcie, I — natężenie prądu elektr.). Jednostką pracy w układzie SI jest dżul.

Siłę potencjalną niezależną od czasu nazywa się siłą zachowawczą. Praca sił zachowawczych jest równa różnicy potencjałów sił w punktach odpowiadających początkowemu i końcowemu położeniu ciała i nie zależy od toru ruchu ciała.

ENERGIA KINETYCZNA, część energii mech. układu fiz. (np. ciała sztywnego) zależna od prędkości jego punktów; w przypadku ciała sztywnego o masie m poruszającego się ruchem postępowym z prędkością v (znacznie mniejszą od prędkości światła) jego energia kinetyczna E _k = mv ²/2; energia kinetyczna ciała sztywnego obracającego się z prędkością kątową ω wokół pewnej osi E _k = Iω ²/2, gdzie I — moment bezwładności ciała względem tejże osi; wg

mechaniki relatywistycznej, gdzie m ₀ — masa spoczynkowa ciała, c — prędkość światła w próżni.

ENERGIA POTENCJALNA, część energii mech. układu fiz. zależna od wzajemnego rozmieszczenia części układu (np. energia sprężysta) i od ich położenia w zewn. polu sił; miarą e.p. jest w danym położeniu jest praca, którą muszą wykonać siły działające na układ, aby przeprowadzić go z położenia, dla którego e.p. przyjmuje się umownie za równą zeru, do danego położenia; np. E_p ciała o masie m w polu grawitacyjnym Ziemi na wysokości h równa jest iloczynowi siły ciężkości mg (g — przyśpieszenie ziemskie) i h:

E_p = mgh.

ENERGII ZACHOWANIA ZASADA, jedno z podstawowych praw fizyki: całkowita energia dowolnego izolowanego (tj. nie oddziałującego z otoczeniem) układu fiz. ma wartość stałą. Jeśli izolowany układ fiz. składa się z wielu oddziałujących wzajemnie podukładów, to energia podukładów może ulegać zmianie, ale całkowita energia wszystkich podukładów musi pozostać nie zmieniona. W procesach fiz. jedna forma energii może zmienić się w inną, np. energia mech. w energię prądu elektr., energia promieniowania elektromagnet. w energię kinet. ruchu cząstki, ale całkowita energia zawsze pozostaje stała.

Zgodnie ze szczególną teorią względności między całkowitą energią E i całkowitą masą układu m istnieje związek E = mc² , przy czym m zmienia się zależnie od prędkości układu (c — prędkość światła w próżni).

POLE GRAWITACYJNE, rodzaj pola fiz.; stan przestrzeni fiz. odznaczający się tym, że na znajdujące się w tej przestrzeni ciała obdarzone masą działa określona siła (grawitacja).

KEPLERA PRAWA, trzy prawa sformułowane (1609-19) przez J. Keplera na podstawie analizy obserwacji ruchu planet;

I prawo Keplera: orbita każdej planety jest elipsą, w której ognisku znajduje się Słońce

II prawo Keplera: promień wodzący planety zakreśla jednakowe pola w równych odstępach czasu (prawo pól);

III prawo Keplera: stosunek sześcianów wielkich półosi a orbit planet do kwadratów okresu T obiegu planet wokół Słońca (a³/T²) jest jednakowy dla wszystkich planet

BRYŁA SZTYWNA, ciało sztywne, ciało, które nie ulega odkształceniu, niezależnie od wartości przyłożonych do niego sił.

MOMENT BEZWŁADNOŚCI, mech. wielkość fiz. charakteryzująca bezwładność bryły sztywnej wykonującej ruch obrotowy; wartość momentu bezwładności zależy od rozmieszczenia masy bryły względem osi obrotu; moment bezwładności bryły względem osi z określa się wzorem:

,
,

gdzie ρ — gęstość materiału elementu bryły, będąca funkcją położenia punktu, V — objętość bryły, m_i — masa i-tego punktu materialnego bryły sztywnej, r_i (lub r) — jego odległość od osi z.

MOMENT SIŁY moment siły względem punktu 0 — wielkość wektorowa
0 równa iloczynowi wektorowemu wektora wodzącego
(poprowadzonego z punktu 0 do punktu przyłożenia siły
) i siły

0 = 
×

moment siły względem osi z, moment rzutu
na płaszczyznę xy (

y) względem punktu przecięcia się osi z tą płaszczyzną. Moment układu sił jest równy wypadkowej momentów sił układu.

EULERA RÓWNANIA RUCHU OBROTOWEGO, różniczkowe równania ruchu ciała sztywnego mającego jeden punkt nieruchomy:

,

,

,

gdzie ω_x, ω_y, ω_z — rzuty chwilowej prędkości kątowej ω na osie gł. wyprowadzone z punktu nieruchomego, I_x, I_y, I_z — momenty bezwładności ciała względem tych osi, M_x, M_y, M_z — momenty sił względem tych osi. Eulera równania ruchu obrotowego całkuje się po dodaniu do nich 3 równań kinematycznych opisujących wartości rzutów ω_x, ω_y , ω_z w zależności od kątów Eulera (φ, ψ,
):

,

,

.

OSCYLATOR [łac.], układ fiz. (mech., elektr.), wykonujący drgania wokół położenia równowagi trwałej. Jeśli na układ mech. wykonujący drgania działa siła proporcjonalna do wychylenia to stanowi on tzw. oscylator harmoniczny; gdy nie występują straty energii (suma energii kinet. i potencjalnej jest stała), oscylator harmoniczny wykonuje drgania niegasnące, o stałej amplitudzie i stałym okresie; w przeciwnym wypadku drgania oscylatora są gasnące (oscylator tłumiony).

WZGLĘDNOŚCI TEORIA,

Za najważniejsze jej konsekwencje uznaje się: uzależnienie czasu przebiegu zjawisk fiz., masy cząstek i wielu innych wielkości od stanu ruchu układu, w którym te zjawiska są opisane; podanie związku E = mc² pomiędzy masą m i energią E ciała; eliminację z fizyki pojęcia eteru i nadanie polom fizycznym statusu samodzielnych obiektów fiz., charakteryzujących się masą, gęstościami pędu, energii, momentu pędu itp.; uznanie pewnych wielkości, uznawanych poprzednio za wielkości odrębne, za składowe jednej wielkości określonej w czasoprzestrzeni. Szczególna teoria względności stanowi podstawę konstrukcji współcz. akceleratorów cząstek, a kinematyka relatywistyczna jest potwierdzona tysiącami doświadczeń nad rozpraszaniem cząstek o wysokich energiach. Zasada względności Einsteina jest we współcz. fizyce przyjmowana jako jedno z podstawowych kryteriów metodol., które powinna spełniać każda teoria. W 1916 Einstein sformułował ogólną teorię względności. W teorii tej zjawisko powszechnego ciążenia jest spowodowane wystąpieniem krzywizny czasoprzestrzeni, która jest przestrzenią bardziej ogólną niż nie mająca krzywizny czasoprzestrzeń Minkowskiego. Właściwości geom. tej ogólnej czasoprzestrzeni zależą od ruchu i rozkładu materii oraz pól, i z kolei same określają ruch materii oraz mają wpływ na pola. Zależność ta jest określona przez równania Einsteina; rozwiązaniami tych równań są czasoprzestrzenie odpowiadające rozmaitym sytuacjom fiz., a jedną z nich, dla przypadku gdy nie ma materii i pól, jest czasoprzestrzeń Minkowskiego. W ogólnej teorii względności nie ma żadnych wyróżnionych układów odniesienia. Pojawiają się one jednak wtedy, gdy rozwiązania równań Einsteina mają pewnego rodzaju symetrie. Ogólna teoria względności przewiduje poprawki do ruchu ciał i światła w polu grawitacyjnym. Ogólna teoria umożliwia m.in. konstruowanie modeli kosmologicznych Wszechświata; jeden z takich modeli tłumaczy zaobserwowane zjawisko ucieczki odległych galaktyk rozszerzaniem się Wszechświata.

LORENTZA PRZEKSZTAŁCENIA, transformacje Lorentza, przekształcenia wiążące składowe wielkości fiz. (położenia, energii-pędu, pola elektromagnet. itp.) w 2 różnych układach inercjalnych. Podstawową rolę odgrywają przekształcenia współrzędnych przestrzenno-czasowych (x, y, z, t) i (x', y', z', t') tego samego zdarzenia w układach inercjalnych K i K'. Jeśli K' porusza się względem K z prędkością v w kierunku osi x, a osie K' i K są równoległe, to obwiązują szczególne przekształcenia Lorentza:

,

,

gdzie c — prędkość światła w próżni; przy prędkościach v << c przekształcenia Lorentza przechodzą w przekształcenia Galileusza. Zasadniczym wynikiem szczególnej teorii względności jest niezmienniczość praw fizyki względem przekształceń Lorentza.

DYLATACJA CZASU, w teorii względności efekt polegający bądź na opóźnianiu się zegara będącego w ruchu w stosunku do zegara spoczywającego w pewnym inercjalnym układzie odniesienia (kinematyczna dylatacja czasu), bądź na opóźnianiu się zegara znajdującego się w silnym polu grawitacyjnym (grawitacyjna dylatacja czasu); oba te efekty zostały zaobserwowane: poruszające się z dużymi prędkościami nietrwałe cząstki elementarne (np. w promieniowaniu kosm.) żyją dłużej niż cząstki spoczywające, natomiast czułe zegary znajdujące się w górach spieszą się w stosunku do zegarów pozostawionych na poziomie morza (będących w silniejszym polu grawitacyjnym — bliżej środka Ziemi).

MASA wielkość fiz. charakteryzująca obiekty fiz., służąca do ilościowego opisu ich bezwładności i oddziaływania grawitacyjnego. Pomiar masy przeprowadza się posługując się II zasadą dynamiki Newtona, bądź wykorzystując zjawisko grawitacji (w tym wypadku porównuje się siły ciężkości działające na ciała materialne w tym samym — w przybliżeniu — punkcie pola grawitacyjnego Ziemi). W mechanice relatywistycznej masa ciała zależy od układu odniesienia, w którym się ją mierzy; między masą m, tzw. masą relatywistyczną ciała, mierzoną w układzie odniesienia, względem którego porusza się ono z prędkością v, a masą m₀ — tzw. masą spoczynkową ciała mierzoną w układzie odniesienia, w którym ono spoczywa, występuje zależność

różnica m i m₀ stanowi tzw. relatywistyczny przyrost masy. Zgodnie ze szczególną teorią względności Einsteina masa i energia są równoważne jeśli ciało ma masę spoczynkową m₀, to odpowiada jej energia E₀ = m₀ c²; masa spoczynkowa cząstek elementarnych może niekiedy całkowicie przejść w postać energii . Obiekt fiz. pozbawiony masy spoczynkowej (foton, neutrino), a mający energię E ma również masę

m = E/c² i pęd p = E/

ENERGIA , skalarna wielkość fiz. służąca do ilościowego opisu różnych procesów i rodzajów oddziaływania; Stwierdzono, że wszystkie postacie ruchu przekształcają się w siebie nawzajem w ściśle określonych stosunkach ilościowych; właśnie ta okoliczność umożliwia wprowadzenie pojęcia energii, czyli pozwala mierzyć różne postacie ruchu i oddziaływania jedną miarą. Różnym rodzajom procesów fiz. odpowiadają różne rodzaje energii: mech., elektromagnet., grawitacyjna, jądr. itd.; rozgraniczenia te nie są jednak ścisłe.

EINSTEINA WZÓR, wzór E = mc² wyrażający związek między całkowitą energią ciała E i jego masą relatywistyczną m (c — prędkość światła w próżni); Ze wzoru Einsteina wynika, że ciało będące w spoczynku ma energię spoczynkową E₀ = m₀c² oraz, że układ mający energię E, ma również masę m = E/c², choćby nie miał masy spoczynkowej (m₀ = 0, jak np. foton, neutrino). Energia spoczynkowa odpowiadająca masie 1 g wynosi 9 · 10¹³ J.

TERMOJĄDROWE REAKCJE, reakcje termonuklearne, fuzja jądrowa, synteza termojądrowa, reakcje jądr. polegające na łączeniu się lekkich jąder atom. w jądra cięższe o większej liczbie atomowej. Ponieważ energia wiązania przypadająca na jeden nukleon wzrasta wraz z liczbą atom., reakcji termojądrowej towarzyszy wydzielanie energii równej przyrostowi całkowitej energii wiązania

Reakcje termojądrowe zachodzą w wyniku zbliżenia się jąder na odległość odpowiadającą zasięgowi sił jądr. (ok. 1 fm), co jest możliwe po pokonaniu elektrostat. bariery kulombowskiej wzajemnego odpychania jąder; reakcje termojądrowe mogą więc zachodzić albo przy dużej energii zderzających się jąder, co odpowiada temp. rzędu 10⁸ K, albo przy zniekształceniu bariery kulombowskiej

Reakcje termojądrowe w gwiazdach są podstawowym źródłem energii i stanowią mechanizm tworzenia pierwiastków chem. (nukleogeneza); np. we wnętrzu Słońca, w temp. 10⁷ K przebiega reakcja syntezy protonów ¹₁H w jądro helu (⁴₂ He), tzw. spalanie wodoru; w gwiazdach o masie kilkanaście razy większej od masy Słońca w temp. powyżej 10⁸ K przebiegają reakcje prowadzące do powstawania jąder ¹²₆C, ¹⁶₈O, ²⁰₁₀N. W warunkach ziemskich reakcje termojądrowe zrealizowano w próbnych wybuchach termojądr.; odpowiednią temperaturę otrzymano na przeciąg ok. 10^-6s w wyniku wybuchu zapalnika atomowego.

COULOMBA PRAWO, określające siłę F wzajemnego oddziaływania (odpychania lub przyciągania) dwóch punktowych ładunków elektr. q₁ i q₂, odległych od siebie o r

i znajdujących się w ośr. o przenikalności elektr. ε
; analogicznym wzorem wyraża się siła wzajemnego oddziaływania dwóch biegunów magnet. (ładunków, mas magnet.).

POLE ELEKTRYCZNE:

1) Jedna z postaci, w której przejawia się pole elektromagnet. działające na spoczywające ładunki elektr.; pole wytworzone przez nieruchome ładunki elektr. stanowi pole elektrostatyczne. Pole elektryczne w dowolnym punkcie jest scharakteryzowane przez wektor natężenia pola elektrycznego
zgodny co do kierunku i równy co do wartości sile, z jaką pole elektryczne działa na umieszczony w tym miejscu jednostkowy punktowy ładunek dodatni:
 = 
/q — ładunek elektr., na który dziala siła
); wewnątrz dielektryka pole elektryczne charakteryzuje wektor indukcji elektrycznej
; w niezbyt wielkich polach elektrycznych w dielektrykach jednorodnych
 = ε₀ ε _r
(ε₀ i ε_r odpowiednio przenikalność elektr. próżni i przenikalność względna danego ośr.); obliczenie natężenia pola elektrycznego w przypadku symetrycznie rozłożonych ładunków elektr. umożliwia prawo Gaussa; oddziaływanie dwóch ładunków elektr. za pośrednictwem pola elektrostat. opisuje prawo Coulomba; pole elektrostat. jest polem zachowawczym, tzn. praca przeniesienia ładunku wzdłuż drogi zamkniętej w tym polu jest równa zeru. Pole elektryczne powoduje przepływ ładunków elektr. w przewodniku, zaś w dielektryku jego polaryzację. Zmienne w czasie pola elektrycznego powodują powstanie pola magnet; jednostką SI natężenia pola elektrycznego jest wolt na metr (V/m).

NATĘŻENIE POLA

1) natężenie pola elektrycznego — wielkość charakteryzująca pole elektr. równa stosunkowi siły działającej na punktowy ładunek elektr. umieszczony w tym polu do wartości tego ładunku;

2) natężenie pola grawitacyjnego — wielkość charakteryzująca pole grawitacyjne równa stosunkowi siły działającej na masę grawitacyjną umieszczoną w tym polu do wartości tej masy; natężenia odpowiednich pól zależą od wielkości i rozmieszczenia wytwarzających te pola ładunków elektr., prądów z nimi związanych i mas grawitacyjnych.

POTENCJAŁ , wielkość pomocnicza służąca do opisu wektorowego pola potencjalnego (zachowawczego, bezwirowego), np. pola grawitacyjnego, elektrostatycznego; potencjał w rozważanym punkcie pola P definiuje się jako całkę krzywoliniową z wektora pola (np. wektora natężenia pola elektrostat.
lub grawitacyjnego) obliczaną wzdłuż drogi L łączącej pewien punkt odniesienia O (zazwyczaj przyjmowany jako punkt położony w nieskończoności) z punktem P; w przypadku pól zachowawczych tak określany potencjał jest niezależny od kształtu drogi całkowania L łączącej punkty O i P i dlatego może służyć do jednoznacznego opisu pola; wartość i zwrot wektora pola w rozważanym punkcie pola można otrzymać z wartości i kierunku maks. spadku potencjału w tymże punkcie (np.
 = -grad V, V — potencjał pola elektrostat.); jeśli rozważane pole zachowawcze jest polem siłowym (np. polem sił grawitacyjnych czy elektrostat.), to potencjał przedstawia sobą pracę przeniesienia ciała próbnego (np. próbnej masy lub próbnego dodatniego ładunku elektr.) przeciwko siłom danego pola od punktu odniesienia O do rozważanego punktu P pola (np. dla pola grawitacyjnego potencjał V = -GM/r, gdzie G — stała grawitacji, M — masa wytwarzająca pole grawitacyjne, r — odległość rozważanego punktu P od środka ciężkości masy M, przy tym za punkt odniesienia przyjęto tu punkt leżący w nieskończoności

GAUSSA PRAWO, Gaussa twierdzenie, strumień wektora indukcji elektr.
przez dowolną powierzchnię zamkniętą jest równy całkowitemu ładunkowi Q zawartemu w przestrzeni V

ograniczonej tą powierzchnią:
, gdzie ρ — gęstość objętościowa ładunku elektr., d
— skierowany element powierzchni; prawo Gaussa jest jednym z podstawowych praw elektrostatyki; umożliwia obliczenie natężenia pól elektrostatycznych.

NAPIĘCIE ELEKTRYCZNE, U, wielkość fiz. skalarna, odnoszona do 2 dowolnych punktów (np. A i B) obwodu elektr. lub pola elektr., równa stosunkowi pracy W, wykonywanej przez siły pola elektr. przy przemieszczaniu ładunku elektr. q wzdłuż pewnej krzywej s (między dwoma wybranymi punktami pola), do wartości tego ładunku:
, gdzie E_s — składowa natężenia pola elektr. wzdłuż elementu drogi ds. W polu elektr. zachowawczym praca nie zależy od drogi, zatem napięcie elektryczne jest równe różnicy potencjałów w tych 2 punktach pola: U_AB  = φ(A) - φ(B).

Jednostką napięcia elektrycznego jest wolt

DIPOL ELEKTRYCZNY, układ 2 jednakowych co do wartości, lecz przeciwnego znaku ładunków elektr. (+Q i -Q) znajdujących się w pewnej odległości l od siebie (np. cząsteczka o rozsuniętym ładunku elektr., tzw. spolaryzowana); wielkością charakteryzującą dipol elektryczny jest dipolowy moment elektryczny
, określony jako wektor skierowany od ładunku ujemnego do dodatniego o wartości µ = Q · l.

POLARYZACJA DIELEKTRYKA, powstawanie elektr. momentu dipolowego dielektryka pod wpływem zewn. pola elektr. Rozróżnia się polaryzację dielektryka deformacyjną i orientacyjną. Polaryzacja orientacyjna (ustawienia) występuje w dielektrykach polarnych i jest wynikiem częściowego uporządkowania słabo związanych cząsteczek polarnych. Miarą polaryzacji dielektryka jest wektor polaryzacji
, określony jako stosunek całkowitego momentu elektr. dielektryka do jego objętości; dla substancji izotropowych
jest proporcjonalne do pola elektr. (ε₀ — przenikalność elektr. próżni, — podatność elektr. ośrodka).

PRZENIKALNOŚĆ ELEKTRYCZNA, przenikalność dielektryczna, ε, wielkość fiz. charakteryzująca właściwości elektr. ośrodka; przenikalność elektryczna ośrodków izotropowych jest skalarem i jest określana wzorem:
 = ε
, gdzie
— indukcja elektr., wywołana polem elektrostat.
; w ośr. anizotropowych przenikalność elektryczna jest tensorem. Do opisu właściwości elektr. ośr. wprowadza się przenikalność elektryczną względną εr przy czym ε = ε₀εr, gdzie ε₀ — przenikalność elektryczna próżni. W układzie SI ε₀ = 8,854 · 10 ^-12 F/m. W ośr. izotropowych εr określa, ile razy większe jest pole elektrostat. w próżni od średniego makroskopowego pola elektrostat. w dielektryku; wartość εr waha się od 1 dla dielektryków gazowych do kilkudziesięciu tys. dla ferroelektryków; dla określonego dielektryka przenikalność elektryczna względna zależy od jego temperatury, przyłożonego ciśnienia, natężenia i częstotliwości przyłożonego pola elektrycznego. Między przenikalnością elektryczną w próżni ε₀ i przenikalnością magnet. próżni µ₀ zachodzi związek ε₀µ₀ = 1/c² (c — prędkość światła w próżni).

POJEMNOŚĆ ELEKTRYCZNA, C, jedna z podstawowych wielkości charakteryzujących elektr. właściwości przewodnika; pojemność elektryczna przewodnika jest równa stosunkowi ładunku q zgromadzonego na przewodniku do potencjału V wywołanego obecnością tego ładunku: C = q/V; zależy od kształtu i rozmiarów przewodnika oraz przenikalności elektr. otaczającego ośrodka. Całkowita pojemność elektryczna równolegle połączonych kondensatorów elektrycznych jest równa sumie ich pojemności elektrycznych: C = C₁ + C₂ +... + Cn; w przypadku kondensatorów połączonych szeregowo zachodzi związek 1/C = 1/C₁ + 1/C₂ +... + 1/Cn. Jednostką pojemności elektrycznej w układzie SI jest farad.

OHMA PRAWO, natężenie prądu elektr. stałego I przepływającego przez przewodnik jest wprost proporcjonalne do napięcia elektr. U na końcach tego przewodnika;

I = U/R

gdzie R — opór elektr.;

KONDENSATOR ELEKTRYCZNY, układ 2 przewodników rozdzielonych warstwą dielektryka, służący do gromadzenia ładunku elektr.; kondemsator elektryczny ładuje się przez przyłączenie do źródła prądu stałego; na jego elektrodach gromadzi się wówczas ładunek elektr., a w dielektryku powstaje pole elektr. o energii

W = ¹/₂CU ²

gdzie: C — pojemność, U — napięcie między elektrodami

POLE MAGNETYCZNE:

pole magnetyczne powstaje wskutek ruchu ładunków elektr. (np. elektronów w atomie, prądu elektr. płynącego w przewodniku; oraz zmian w czasie pola elektrycznego. Pole magnetyczne w każdym punkcie przestrzeni charakteryzują wektor indukcji magnet.
, definiowany poprzez siłę
, z jaką pole magnetyczne działa na poruszający się z prędkością
ładunek elektr. q

= q
×

oraz — niezależny od magnet. właściwości ośr. — wektor natężenia pola magnetycznego
; dla dia- i paramagnetyków
 = µ₀ µr H (µ₀, µ_r odpowiednio przenikalność magnet. próżni i przenikalność względna ośrodka). Pole magnetyczne jest polem bezźródłowym; linie pola magnetycznego są zamknięte lub biegną do nieskończoności. Jednostką SI indukcji magnet. jest tesla (T), jednostką natężenia pola magnet. — amper na metr (A/m).

SIŁA LORENTZA, siła
, z jaką pole elektromagnet. działa na poruszającą się cząstkę naładowaną:

= q
 + q
×

gdzie q — ładunek elektr. cząstki,
— natężenie pola elektr.,
— indukcja magnet.,
— prędkość cząstki; pierwszy składnik wzoru przedstawia siłę działającą na cząstkę w polu elektr., drugi — siłę działającą w polu magnet. (powoduje ona zakrzywienie toru cząstki);

AMPÈRE'A REGUŁA, reguła określająca zależność między kierunkiem prądu elektr. i kierunkiem pola magnet. wytworzonego przez ten prąd; znana w 2 sformułowaniach: 1) reguła pływaka — obserwator płynący wzdłuż przewodu zgodnie z kierunkiem prądu elektr. tak, że jest zwrócony twarzą ku igle magnet., umieszczonej pod przewodem, widzi biegun pn. tej igły odchylony w lewo od kierunku, w którym płynie; 2) reguła korkociągu, reguła śruby prawoskrętnej — zwrot linii pola magnet. wytworzonego przez prąd elektr. w przewodzie wyznacza ruch obrotowy śruby prawoskrętnej, wkręcanej w ten sposób, że jej ruch postępowy jest zgodny z kierunkiem prądu w przewodzie.

DIPOL MAGNETYCZNY, układ fiz. wytwarzający w przestrzeni takie pole magnet. jak 2 blisko siebie położone, przeciwnego znaku masy magnet. (ładunki magnet.; umowne odpowiedniki ładunku elektr. w magnesie trwałym); dipole magnetyczne złożone z mas magnet. w przyrodzie nie występują, w skali mikroskopowej dipolami magnetycznymi są cząstki elementarne o niezerowym spinie, w skali makroskopowej — magnesy sztabkowe, koliste obwody prądu elektr.; wielkością charakteryzującą dipol magnetyczny jest dipolowy moment magnetyczny.

PRZENIKALNOŚĆ MAGNETYCZNA, μ, wielkość fiz. charakteryzująca właściwości magnet. ośr.; określa zdolność ośr. do zmiany indukcji magnet.
pod wpływem zewn. pola magnet. o natężeniu
; przenikalność magnetyczna ośrodków izotropowych jest skalarem i jest określona wzorem:
 = μ
; w ośr. anizotropowych przenikalność magnetyczna jest tensorem. Ze względu na wartość μ_ρ ciała dzielą się na diamagnetyki (μ_ρ< 1), paramagnetyki (μ_ρ > 1) i ferromagnetyki (μ_ρ > 1). Przenikalność magnetyczna mierzona w stałym polu magnet. nazywa się przenikalnością magnetyczną statyczną, a w polu zmiennym przenikalnością magnetyczną dynamiczną

INDUKCJA ELEKTROMAGNETYCZNA, powstawanie siły elektromotorycznej (SEM) E w obwodzie elektr. obejmującym zmienny strumień magnet.; indukcja elektromagnetyczna jest wynikiem działania siły Lorentza na elektrony przewodnika znajdującego się w zmiennym polu magnet.; wartość SEM zależy od szybkości zmian strumienia magnet. Φ:

kierunek prądu indukcyjnego określa reguła Lenza; rozróżnia się indukcję elektryczną wzajemną, gdy zmienne pole magnet., powstałe wokół obwodu 1 z prądem elektr. o zmiennym natężeniu, indukuje SEM w sąsiednim obwodzie 2, oraz indukcję elektryczną własną, tzw. samoindukcję, polegającą na powstawaniu SEM w tym obwodzie, który to zmienne pole magnet. wytworzył; siła elektromotoryczna samoindukcji

gdzie L indukcyjność, dI/dt — szybkość zmian natężenia prądu elektrycznego

MAXWELLA RÓWNANIA, podstawowe równania klas. teorii pola elektromagnet.:

Maxwella wyrażają ścisły związek między polem elektr. i magnet.: (1) pole magnet. zależy od wywołującego je prądu elektr., (2) pole elektr. może być bezźródłowe i wytworzone tylko przez zmienne w czasie pole magnet., (3) źródła pola elektr. znajdują się w punktach, w których są umieszczone ładunki elektr., (4) pole magnet. jest zawsze polem bezźródłowym. Pola elektr. i magnet. są 2 różnymi postaciami pola elektromagnetycznego. Podstawowym wnioskiem wynikającym z równań Maxwella jest istnienie fal elektromagnet.

---