RODZAJ CZWÓRNIKA |
|
Z OBLICZEŃ |
|
|
|||
|
Z1 |
Z2 |
Z3 |
Z4 |
|||
|
[Ω] |
[Ω] |
[Ω] |
[Ω] |
|||
Typ T |
|
|
|
---------------- |
|||
Typ Π |
|
|
|
---------------- |
|||
Typ X |
|
|
|
---------------- |
|||
Obliczenia:
![]()
Czwórnik T |
Czwórnik Π |
|
|
|
|
![]()
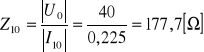
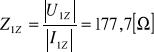
Z opisu czwórnika za pomocą równań z macierzy impedancyjnej mamy:
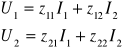
Zatem
![]()
![]()
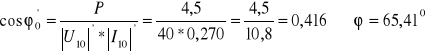
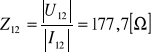
![]()
![]()
Dla wartości zadanych w ćwiczeniu otrzymujemy więc:
![]()
![]()
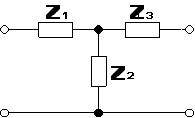
Czwórnik T: (zakładamy że ![]()
)
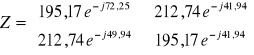
![]()
Posługując się macierzami łańcuchowymi opisanymi w teoretycznej części ćwiczenia otrzymujemy następujące zależność:
![]()
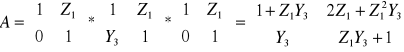
Z tablic przejścia otrzymujemy: ![]()
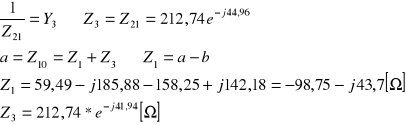
Część rzeczywista impedancji ![]()
jest ujemna co powoduje iż czwórnik ten jest nie możliwy do realizacji.
Czwórnik Π: (zakładamy że ![]()
)
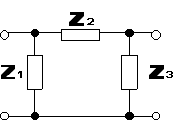
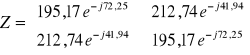
![]()
Posługując się macierzami łańcuchowymi opisanymi w teoretycznej części ćwiczenia otrzymujemy następujące zależność:
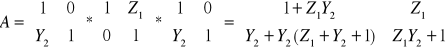
Z tablic przejścia otrzymujemy: ![]()
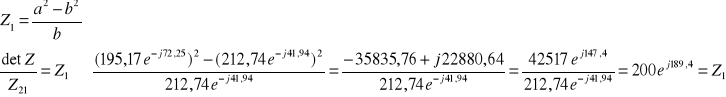
Z tablic przejścia otrzymujemy:
![]()
![]()
![]()
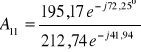
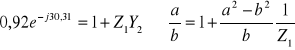
![]()
![]()
![]()
![]()
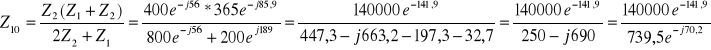
![]()
Obliczenia impedancji falowej:
![]()
Obliczanie ![]()
Dla czwórnika „T”
![]()
Dla czwórnika „Π”
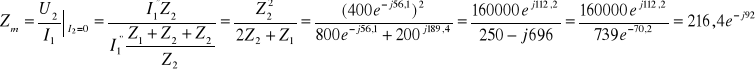
Wyznaczanie g dla czwórnika typu „Π”
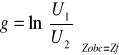
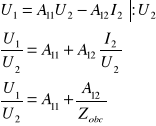
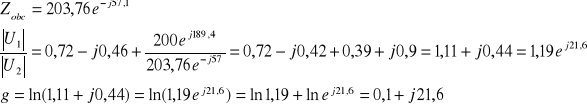
Wyznaczanie miary przenoszenia ze wzoru
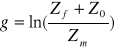
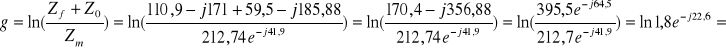
![]()
dla α=Re{g}=1 wyznacz
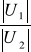
=?
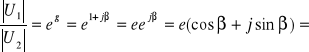
1,04
dla β=Im{g}=0.86 rad , wyjaśnij co to oznacza dla kątów fazowych napięcia wejściowego i wyjściowego
Współczynnik β nazywany jest potocznie przesuwnością i określamy go jako ![]()
w naszym przypadku istnieje to przesunięcie pomiędzy napięciem wejściowym a wejściowym i wynosi ono w przybliżeniu ![]()
.
Wnioski
Przeprowadzone pomiary czwórnika pasywnego symetrycznego pozwoliły określić schematy zastępcze czwórników równoważnych w różnych konfiguracjach układowych.
Analiza otrzymanych wartości impedancji wejściowej w stanie rozwarcie i zwarcia wyjścia pozwala całościowo określić wszystkie parametry czwórnika symetrycznego, w tym jego impedancję falową i współczynnik przenoszenia oraz opisać go odpowiednimi równaniami matematycznymi stosując jedne z sześciu układów równań opisujących te układy. Symetria, czyli brak wyróżnionej pary wejściowej i wyjściowej pozwala znacznie uprościć analizę czwórnika (zmniejsza liczbę równań oraz liczbę pomiarów), ponadto przyczynia się do dużej łatwości łączenia takich czwórników kaskadowo, z zachowaniem jednakowego obciążenia falowego.
Rozpatrywany przez nas czwórnik, którego schematu budowy nie znaliśmy można zastąpić innymi czwórnikami równoważnymi o danych topologiach układu. Po przeprowadzeniu odpowiednich obliczeń i przekształceń otrzymaliśmy wartości impedancji czwórników symetrycznych typu T, Π .
Otrzymane wyniki wskazują, że nie zawsze dany czwórnik pasywny możemy zastąpić innym o odmiennej topologii, stosując tylko elementy bierne. Wnioskujemy to na podstawie ujemnych wartości oporów czynnych, które były rozwiązaniami topologii niektórych typów czwórników. Okazuje się, że badany czwórnik możemy zrealizować, korzystając tylko z elementów pasywnych, we wszystkich trzech podstawowych konfiguracjach układowych, choć nie dla wszystkich możliwych kombinacji wartości elementów. Takim przykładem nie możliwym do realizacji był czwórnik typu T, ponieważ uzyskaliśmy tam ujemną wartość rezystancji. Problem ten teoretycznie mógłby zostać rozwiązany po zastosowaniu diody tunelowej, która posiada ujemną rezystancją, aczkolwiek rezystancja ta jest rezystancją dynamiczną co dyskwalifikuje ją w naszych rozważaniach. Ujemną rezystancję moglibyśmy jednak uzyskać stosując specjalne układy wzmacniaczy operacyjnych (a właściwie ich schematów zastępczych ) które to pozwalają na uzyskanie ( w drodze symulacji) ujemnych rezystancji. Wracając jednak do tematu ćwiczenia w którym to rozpatrujemy pasywne czwórniki wprowadzenie wzmacniacza operacyjnego uczyniło by ten czwórnik aktywnym co także prowadzi do dyskwalifikacji tej metody.
Wyznaczona wartość współczynnika tłumienia wskazuje, że badany czwórnik jest czwórnikiem tłumiącym sygnał wejściowy, gdyż sygnał wyjściowy ma wartość mniejszą od wymuszenia. Kąt przesunięcia fazowego wskazuje na duże przesunięcie fazowe napięcia wyjściowego w stosunku do wejściowego.
Analizując pomiary musimy zauważyć, że ich dokładność była niska. Szczególnie mało wiarygodny był wynik pobieranej przez układ mocy czynnej, jako że odchylenie wskazówki watomierza było niewielkie. W ćwiczeniu do pomiarów mocy czynnej posłużyliśmy się dwoma watomierzami, aby w możliwie jak największym stopniu wyeliminować błąd w pomiarach (wskazania okazały się zbliżone stąd jak możemy się domyślać watomierze miały różną obciążalność). W rezultacie stawia to dużą wątpliwość wobec wiarygodności wyznaczenia oporu czynnego, a tym samym dokładności dalszych obliczeń. Uogólniając - otrzymane wyniki nawet mimo uśrednienia nie pozwalają na dokładne określenie parametrów czwórników zastępczych, preferowalibyśmy zatem używanie cyfrowych przyrządów pomiarowych lub tak jak to miało miejsce dokonywać analizy poszczególnych czwórników za pomocą wcześniej określonych impedancji.
Podsumowując, w ćwiczeniu przeprowadziliśmy analizę czwórnika pasywnego i stworzyliśmy schematy zastępcze czwórników równoważnych oraz wskazaliśmy na możliwość ich praktycznej realizacji., co było zadaniem w przeprowadzonym przez nas ćwiczeniu.
1
6
![]()
![]()
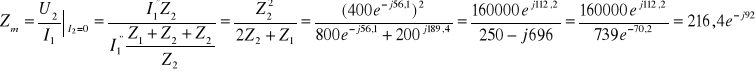
Wyszukiwarka
Podobne podstrony:
czworniki (Daniel3), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08. Czwór
czwórniki - matej, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08. Czwórni
Czwórniki równoważne - a, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08.
Czwórniki równoważne, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08. Czwó
Czwórniki równoważne - c, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08.
Czw orniki równoważne - g, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08.
Czwórniki równoważne - d, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 08.
Twierdzenie Tevenina i Nortona Bob (3), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Lab
Twierdzenie Tevenina i Nortona Bob (1), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Lab
Tabelka ćw 4, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 04. Poprawianie
cw3teor, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 03. Źródło rzeczywist
Wygładzanie tętnień prądu - wykresy - Maciek, Politechnika Poznańska, Elektrotechnika, Teoria obwodó
Układy trójfazowe niesymetryczne - j, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Labor
Poprawa współczynnika mocy, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 04
Rezonans w obwodzie szeregowym(1), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laborato
Thevenin (Tomaj), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 02. Twierdze
stany nieustalone, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 12. Stany n
Poprawianie współczynnika mocy, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria
Rezonans (Owca), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 06. Rezonans
więcej podobnych podstron