LABORATORIUM PODSTAW METROLOGII M-T

Ćwiczenie nr 1

OPRACOWANIE WYNIKÓW POMIARU

1. Błędy pomiaru

Celem pomiaru jest znalezienie wartości miary wielkości mierzonej. Najczęściej surowy wynik pomiaru X jest jedynie przybliżeniem wartości rzeczywistej (prawdziwej) X_rz wielkości mierzonej X. Różnica pomiędzy wynikiem pomiaru X a wartością rzeczywistą X_rz nazywana jest błędem bezwzględnym E_X

(1)

Wartość rzeczywista wielkości mierzonej jest znana tylko w wyjątkowych przypadkach. Dlatego pojęcie błędu E_X ma niewielkie znaczenie praktyczne. W praktyce, w zależności od wymaganej dokładności pomiaru, doświadczenie pomiarowe modyfikuje się tak, aby otrzymać wartość najbliższą X_rz. Wartość tę nazywa się wartością poprawną X_pop. Wtedy wyrażenie na błąd bezwzględny ma postać.

(2)

Błąd ze znakiem przeciwnym nazywany jest poprawką

(3)

Poprzez dodanie poprawki (z uwzględnieniem znaku) do wyniku pomiaru otrzymuje się tzw. wynik skorygowany - czyli wartość poprawną.

Błąd względny e_X jest to stosunek błędu bezwzględnego do wartości poprawnej

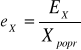
(4)

Błąd względny jest często wyrażany w procentach (1 % = 10^-2) lub promilach (1 ‰ = 10^-3). Spotykane są także określenia: ppm (ang. part per million; 1 ppm = 10^-6) oraz ppb (ang. part per billion; 1 ppb = 10^-9).

W zależności od przyczyny powstawania błędy dzieli się na błędy modelowe oraz błędy instrumentalne. Błędy modelowe są następstwem różnicy pomiędzy rzeczywistym układem warunków fizycznych, w jakich realizowany jest pomiar, a modelem tych warunków, który został przyjęty jako prawdziwy. Na przykład pomiar objętości wałka na podstawie pomiaru jego długości i średnicy może prowadzić do błędu modelowego, jeśli wałek nie ma kształtu walca. Udoskonalając model można wyznaczyć wartość błędu modelowego i za pomocą poprawki skorygować wynik. Błędy instrumentalne są związane z niedokładnością przyrządów pomiarowych. Błędy te powinny być określone przez producenta przyrządu pomiarowego.

Wyznaczanie błędów może się odbywać w dwojaki sposób:

1. Poprzez analizę warunków fizycznych w których przeprowadzany jest pomiar i porównanie ich z warunkami które zostały przyjęte jako warunki modelowe, czyli warunki odniesienia. Różnice wynikać mogą zarówno z braku tożsamości pomiędzy definicją masurandu a realnie mierzona wielkością jak i z wpływu czynników zewnętrznych (wielkości wpływających). Błędy takie nazywa się błędami modelowymi i dotyczą one zarówno koncepcji przeprowadzenia pomiaru ( błędy metody) jak i narzędzi użytych do pomiaru ( błędy instrumentalne). Ich wykrycie i uwzględnienie w wyniku pomiaru poprzez wprowadzenie poprawek jest możliwe jedynie pod warunkiem posiadania wystarczająco wiarygodnych danych o mechaniźmie wpływu poszczególnych czynników na wynik pomiaru i prawidłowego ustalenia modelu pomiaru.

2. Poprze wzorcowanie, czyli porównanie uzyskanego wyniki pomiaru z wartością znaną z innego źródła z większą dokładnością ( wzorzec, wartość zmierzona dokładniejszym przyrządem, dokładniejszą metodą itp.). Wzorcowanie dokonane w określonych warunkach fizycznych przy określonych wartościach wielkości wpływających upoważnia do wprowadzenia poprawek obowiązujących jedynie w tych samych warunkach. Wzorcowanie prowadzi głównie do wykrycia błędów instrumentalnych. Modelowe błędy metody zazwyczaj nie dają się wykryć w ten sposób, gdyż użyty wzorzec jest z reguły bardziej zbliżony do założonego modelu niż praktycznie mierzone wielkości w trakcie eksploatacji systemu pomiarowego.

We współczesnych systemach pomiarowych zapewnienie możliwości wprowadzenia wszelkich możliwych poprawek jest obowiązkiem projektanta systemu. Nie wszystkie jednak poprawki mogą być wprowadzane automatycznie (systemowo) gdyż producent systemu nie wie jak system będzie wykorzystywany przez użytkownika i wobec tego jakie będą błędy modelowe. Dlatego też każdy użytkownik każdego narzędzia pomiarowego powinien posiadać podstawową wiedzę o występowaniu błędów i możliwości wprowadzania poprawek.

2. Niepewność pomiaru.

Dążenie do usunięcia wszystkich błędów jest z reguły niecelowe, gdyż w miarę zwiększania precyzji narzędzi pomiarowych stosowanych w doświadczeniu ujawnia się wpływ zmian różnych wielkości wpływających na jego wynik. Są one przyczyną rozproszenia wyników pomiaru którego miarą jest niepewność wyniku pomiaru.. Rozproszenie wyników pomiaru ma charakter losowy, a zatem jego miara w postaci niepewności jest miarą statystyczną. Wyróżnia się dwa rodzaje niepewności: niepewność typu A oraz niepewność typu B.

Do grupy A zalicza się niepewności, które ujawniają się przy powtarzaniu pomiaru w tych samych warunkach. Ich rozkłady statystyczne teoretycznie mogą być zatem oszacowane na podstawie wykonanych pomiarów. Wyznaczenie niepewności typu A wymaga wykonania serii pomiarów, w celu ujawnienia losowego charakteru ich zmian. Podstawą do oceny niepewności typu A jest zbiór wyników pomiarów przy użyciu którego wykonuje się następujące obliczenia: wyznacza się wartość średnią według równania (8), niepewność pojedynczego wyniku wg wzoru (15), niepewność wartości średniej ze wzoru (18) oraz ustala się przedział niepewności zależny od wymaganego przedziału ufności.

Do niepewności typu B zalicza się niepewności nie ujawniające się przy powtarzaniu pomiarów. Ich źródłem są nie do końca skorygowane błędy, a zatem niewiedza odnośnie różnicy pomiędzy wartością rzeczywistą a poprawną, niewiedza odnośnie warunków pomiaru i ich wpływu na wynik, niepewności użytych wzorców w procesie wzorcowania itp. Dane do wyznaczenia niepewności typu B winy być podane w dokumentacji systemu pomiarowego, świadectwach wzorcowania, w normach i tablicach. z których pochodzą wartości niezbędnych współczynników (np. przyspieszenia ziemskiego).

Rozkłady niepewności typu A są znane nieprecyzyjnie gdyż liczba wykonanych pomiarów jest zazwyczaj niewielka. Rozkłady niepewności typu B są z reguły w ogóle nie znane. Jednakże wówczas, gdy liczba czynników wpływających na niepewność pomiaru jest znaczna, a ponadto czynniki te oddziaływują w sposób niezależny i losowy to można przyjąć iż wartości wyników pomiaru podlegają rozkładowi normalnemu (Gaussa). Wynika to z centralnego twierdzenia granicznego rachunku prawdopodobieństwa.

3. Rozkład normalny

Krzywa rozkładu normalnego gęstości g(X) wyników pomiarów ma charakterystyczny kształt dzwonowy (rys.1).

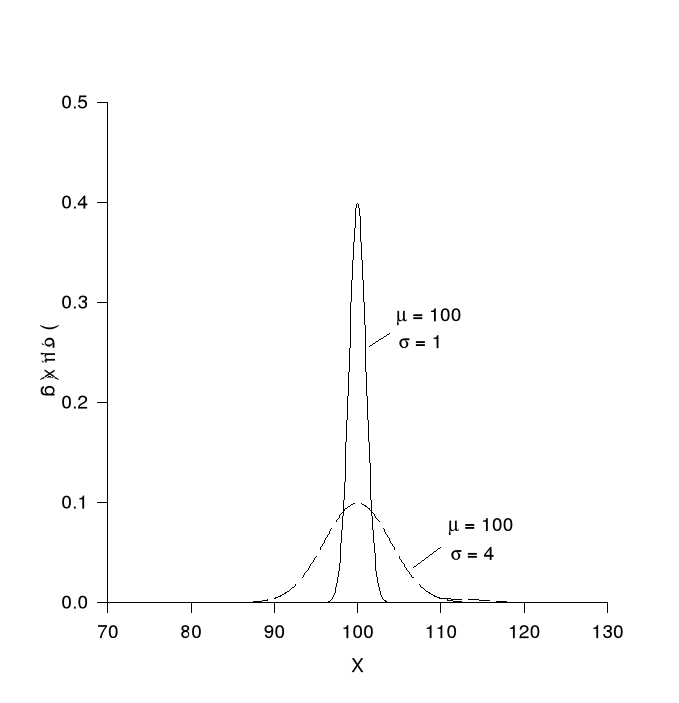
Rys.1 Krzywa rozkładu normalnego (Gaussa)

Równanie krzywej dzwonowej ma ogólną postać

(5)

gdzie μ jest wartością oczekiwaną (wartością średnią), a σ²jest wariancją. Zmiana parametru μ powoduje przesunięcie krzywej wzdłuż osi odciętych. Zmiana parametru σ powoduje zmianę kształtu krzywej: im σ jest mniejsze, tym krzywa jest bardziej smukła. Prawdopodobieństwo P tego, że wartość x zawierać się będzie w przedziale jest równe zaczernionemu polu pod krzywą na rys. 2.

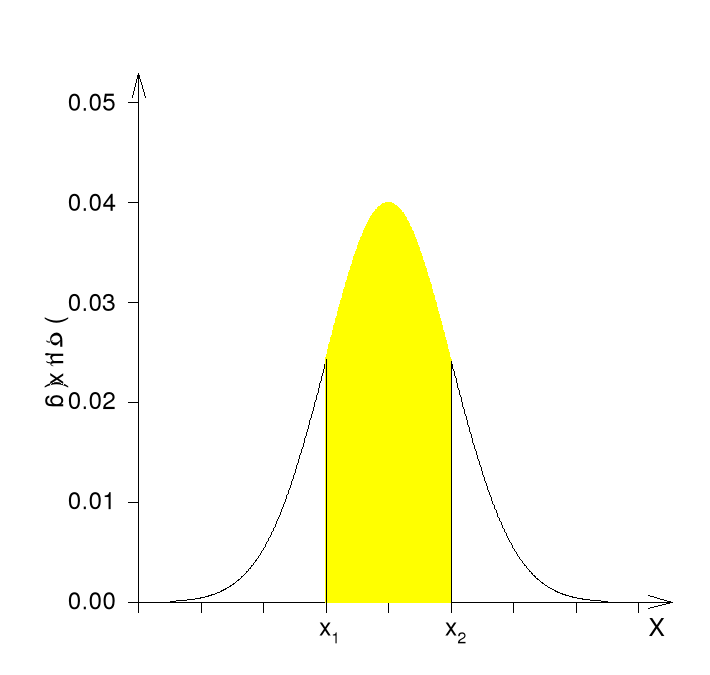
Rys. 2 Pole powierzchni zaczernionego obszaru odpowiada prawdopodobieństwu znalezienia się wyniku pomiaru w przedziale

Pole to jest równe

(6)

Całkę tę można obliczyć metodą numeryczną lub, po wprowadzeniu zmiennej odczytać z tablic wartość całki unormowanej funkcji .

Centralizując zmienną X wokół wartości średniej i wprowadzając oznaczenia oraz otrzymuje się krzywą rozkładu normalnego niepewności:

(7)

Przedstawiono ją na rysunku 3. Na rysunku tym zaznaczono pole odpowiadające prawdopodobieństwu 0,68 (poziomowi ufności 68%). Jest to prawdopodobieństwo wystąpienia błędu przypadkowego pojedynczego pomiaru w przedziale , odpowiadające tak zwanej niepewności standardowej (1σ - jednosigmowej). Najczęściej do określania niepewności wyników pomiarów stosowana jest niepewność rozszerzona czyli przemnożona przez współczynnik rozszerzenia k. W przypadku k=2 otrzymuje się niepewność której odpowiada poziom ufności 95 %. (2σ - dwusigmowa). W przypadku k=3 poziom ufności wzrasta do 99,73 % (3σ - trzysigmowa). Podane poziomy ufności obowiązują jedynie przy założeniu rozkładu normalnego.

Parametry x_popr oraz są estymatorami (oszacowaniami) odpowiednio: wartości oczekiwanejμ iwariancji σ², których wartości rzeczywiste są nieznane.

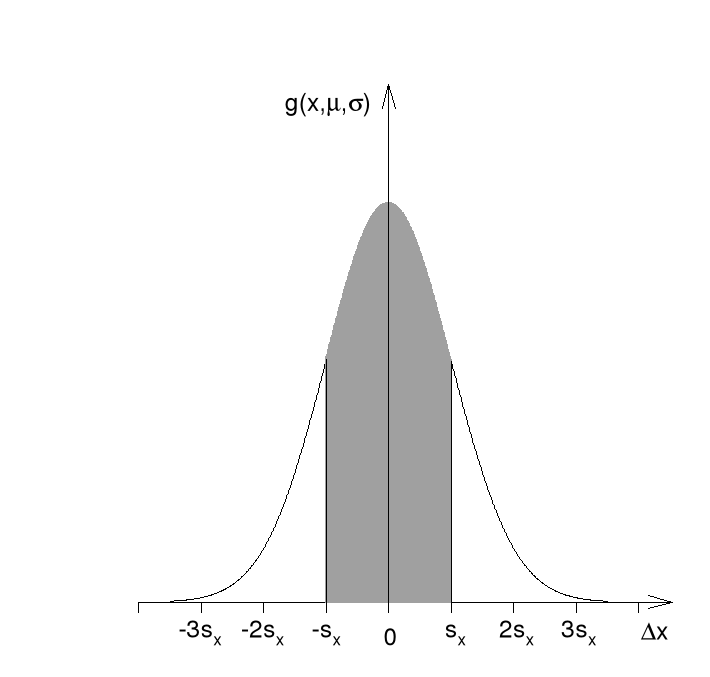
Rys.3 Pole powierzchni zaczernionego obszaru odpowiada prawdopodobieństwu P = 0,68 wystąpienia błędu przypadkowego w przedziale

Wartość oczekiwana jest miarą skupienia rozkładu. Dla zmiennej losowej skokowej, wartość oczekiwana jest równa średniej arytmetycznej

(8)

gdzie n jest liczbą pomiarów, a.- i-tym wynikiem pomiaru. Dla zmiennej losowej ciągłej wartość oczekiwana jest dana wzorem

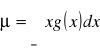
(9)

Wariancja jest miarą rozproszenia rozkładu. Dla zmiennej skokowej wariancję oblicza się ze wzoru

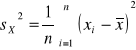
(10)

Dla zmiennej losowej ciągłej wariancja jest równa

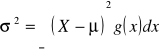
(11)

Estymatorem wartości oczekiwanej jest najczęściej średnia arytmetyczna , wyrażona wzorem

(12)

gdzie n jest liczbą wszystkich wyników pomiaru, a i jest numerem wyniku. Estymatorem wariancji jest wariancja empiryczna, dana równaniem

- dla n  30 (wariancja empiryczna nieskorygowana) (13)

- dla n < 30 (wariancja empiryczna skorygowana) (14)

Pierwiastek kwadratowy z wariancji empirycznej jest nazywany odchyleniem standardowym

(15)

Parametr ten jest oszacowaniem niepewności pojedynczego wyniku.

Rozrzut wartości średniej wyników charakteryzuje wariancja empiryczna dla średniej

- dla n  30 (nieskorygowana) (16)

- dla n < 30 (skorygowana) (17)

Pierwiastek kwadratowy z wariancji empirycznej dla średniej jest nazywany rozproszeniem wartości średniej lub odchyleniem standardowym dla średniej

(18)

Parametr ten jest oszacowaniem niepewności wartości średniej wyników.

W przypadku małej liczby (n < 30) wyników pomiaru parametry μ, σ rozkładu mogą się znacznie różnić od ich estymatorów i s. W takim przypadku, w celu zwiększenia wiarygodności wyników korzysta się z rozkładu t-Studenta [1].

3. Rozkład jednostajny

Analiza przyczyn niepewności wywołanych jednym czynnikiem może czasami doprowadzić do wniosku o występowaniu całkiem innego rozkładu gęstości prawdopodobieństwa, a mianowicie rozkładu jednostajnego przedstawionego na rys.4.

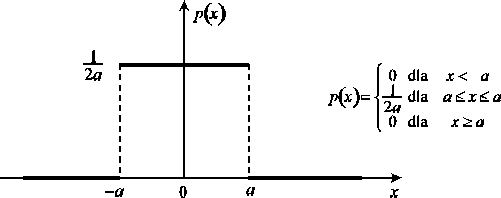
Rys.4 Rozkład jednostajny

Dla rozkładu jednostajnego o szerokości przedziału 2a wariancję i odchylenie standardowe pojedynczego wyniku oblicza się ze wzorów:

(19)

(20)

Jeśli niepewność wyniku nie jest określona i nie ma możliwości jej oceny, to przedział niepewności określa się na podstawie liczby cyfr znaczących wyniku. Jeśli wynik został prawidłowo zaokrąglony, to przyjmuje się iż wartość odpowiadająca jedynce na ostatnim miejscu znaczącym stanowi przedział o szerokości 2a, a rozkład niepewności jest jednostajny. Są to dość arbitralne założenia, ale często uznawane za uzasadnione.

3. Niepewność wyników pomiarów pośrednich

Wartość wielkości może być zmierzona bezpośrednio (np. pomiar długości za pomocą suwmiarki) lub pośrednio (np. pomiar objętości walca przez pomiar jego długości i średnicy), a następnie obliczenie objętości z odpowiedniego wzoru).

Niepewność wartości y wyznaczanej ze wzoru , w którym występuje k wielkości x_i, z których każda charakteryzuje się niepewnością
, oblicza się ze wzoru

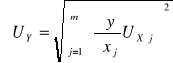
(21)

Wzór ten obowiązuje w przypadku, gdy niepewności
dotyczą nieskolerowanych (niezależnych od siebie) zmiennych losowych i wyrażone są poprzez odchylenia standardowe.

Jeśli funkcja jest jednomianem algebraicznym postaci

(22)

tzn. zawiera tylko działania mnożenia, dzielenia, potęgowania lub pierwiastkowania, to zamiast wzoru (21) korzystniej jest stosować zależność, w której występują niepewności względne
. Niepewność względną definiuje się jako stosunek niepewności bezwzględnej do wartości poprawnej.

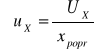
(23)

Wówczas niepewność względną wyniku pośredniego oblicza się jako

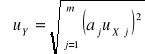
(24)

4. Praktyczny algorytm opracowania wyników pomiaru

Opracowanie końcowego wyniku pomiaru nie może być sprowadzone do jednego, stałego algorytmu postępowania. Sposób opracowania wyników pomiaru powinien być modyfikowany w zależności od specyfiki doświadczenia pomiarowego. Zaprezentowany, uproszczony algorytm realizowany jest w kilku etapach:

1°Ustalenie wartości poprawnych wielkości mierzonych bezpośrednio. Wielkością poprawną może być:

a) pojedyncze wskazanie przyrządu. Przypadek występuje, gdy np. przyrząd jest zalegalizowany i nie ma żadnych dodatkowych powodów, aby wynik musiał być skorygowany. Pomiar taki sprzyja powstaniu błędu nadmiernego (np. na skutek omyłki obserwatora);

b) średnia arytmetyczna wskazań przyrządu (wzór 8). Przypadek występuje przy powtarzaniu pomiarów, które charakteryzują się rozrzutem, a jednocześnie nie ma powodów lub możliwości wprowadzenia poprawek;

c) skorygowane pojedyncze wskazanie przyrządu lub skorygowana średnia arytmetyczna. Korekcja polega na dodaniu odpowiednich poprawek. Poprawki uwzględnia się w trzech przypadkach:

- gdy są one podane (np. w formie tabeli lub wykresów);

- gdy można je obliczyć (np. błąd spowodowany zmianą temperatury, błąd metody);

- jeśli dokonało się wzorcowania przyrządu.

2°Ustalenie niepewności wielkości otrzymanych bezpośrednio. Najczęściej wyznacza się przedział ograniczony odchyleniem standardowym. W przypadku rozkładu normalnego z prawdopodobieństwem P=0,68 znajduje się w nim poprawna wartość mierzonej wielkości. Jest to tzw. niepewność standardowa, która charakteryzuje rozproszenie (losowy charakter) wyników. Oblicza się ją ze wzoru (18). Jest to niepewność typu A.

Na całkowitą (łączną) niepewność
wyniku wpływa wiele czynników, między innymi dokładność przyrządu pomiarowego (podana w jego dokumentacji), nieznane zmiany wielkości wpływowych (np. temperatury), zmiany wielkości mierzonej. Ocena niepewności całkowitej wymaga uwzględnienia wszystkich istotnych czynników. Aby obliczyć niepewność łączną, należy najpierw wyznaczyć poszczególne odchylenia standardowe i skorzystać ze wzoru

(25)

3°O ile jest to potrzebne - obliczenie wartości poprawnej wielkości mierzonej pośrednio. Jeśli argumentami danej funkcji y wyrażającej wielkość mierzoną pośrednio są wartości x_j (j=1, 2, ...m), to szukaną wartość wyznacza się ze wzoru:

(26)

4°O ile jest to potrzebne - obliczenie niepewności łącznej (całkowitej) wielkości mierzonej pośrednio ze wzoru

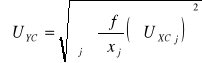
(27)

gdzie
są wyznaczonymi w drugim kroku niepewnościami łącznymi poszczególnych wielkości mierzonych bezpośrednio.

5°Obliczenie niepewności rozszerzonej do określonego poziomu ufności ze wzoru

(dla wielkości mierzonej bezpośrednio) (28)

(dla wielkości mierzonej pośrednio) (29)

Tablica 1 Zestawienie najczęściej spotykanych wartości poziomów ufności

i odpowiadających im kwantyli dla rozkładu normalnego

Poziom ufności	Nazwa przedziału niepewności	Kwantyl t
68 %	1σ (standardowy)	1
95 %	2σ	2
99,73 %	3σ (graniczny)	3

gdzie t jest kwantylem zależnym od przyjętego poziomu ufności. Kwantyle nazywa się czasami współczynnikami rozszerzenia i ozncza literą k. Wartości kwantyli dla najczęściej stosowanych poziomów ufności przedstawiono w tablicy 1.

Graficzną interpretację relacji występujących między parametrami wyniku przedstawiono na rysunku5.

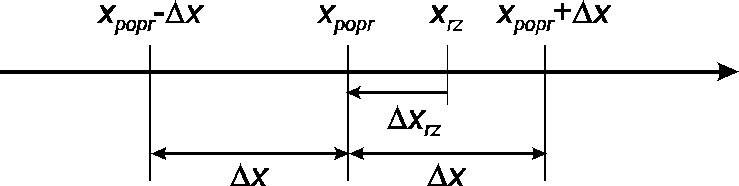
Rys.5 Interpretacja relacji występujących między parametrami wyniku

Na rysunku5 punkty i wyznaczają granice przedziału, w którym z określonym prawdopodobieństwem znajduje się wartość poprawna x_pop. Parametr może być utożsamiany z niepewnością rozszerzoną. Z rysunku wynika, iż w przypadku nie przeprowadzenia, lub niedostatecznego przeprowadzenia korekcji błędu i nie uwzględniania tego faktu przy analizie niepewności, wartość rzeczywista może się znaleźć poza wyznaczonym zakresem niepewności. Z tego względu przy analizie składników niepewności należy zawsze bardzo starannie rozpatrzyć jakość przeprowadzonej korekcji błędów.

5. Zapis wyniku pomiaru

Prawidłowo zapisany wynik pomiaru powinien składać się z dwóch liczb, z których pierwsza wyraża poprawną wartość wielkości mierzonej, a druga określa jej niepewność. Ponadto ze sposobu zapisu musi wynikać prawdopodobieństwo (poziom ufności), z jakim wartość poprawna znajdzie się w przedziale niepewności. Ogólnie zapis końcowego wyniku pomiaru powinien mieć postać następującą

(informacja o poziomie ufności)

Z zapisem związane jest prawidłowe zaokrąglenie wyniku pomiaru. Najpierw zaokrągla się niepewność, najczęściej „w górę” do jednej, w wyjątkowych przypadkach do dwóch cyfr znaczących. Następnie zaokrągla się liczbę wyrażającą wartość wielkości, pozostawiając ostatnią cyfrę znaczącą na tym miejscu, na którym występuje niepewność.

Przykłady prawidłowego zapisu końcowego wyniku pomiaru:

a) Wynik pomiaru długości:

l = (23,45 ± 0,01)mm; (niepewność standardowa)

zapis równoważny:

l = (23,45 ± 0,03) mm; (niepewność graniczna)

zapis równoważny przy użyciu niepewności względnej:

l = 23,45 (1 ± 5⋅10^-4) mm; (niepewność graniczna)

Ostatnia forma zapisu nie jest polecana gdyż może prowadzić do niejasności.

Przykład 1

Woltomierzem cyfrowym o zakresie 10 V wykonano 10 pomiarów napięcia. Średnia arytmetyczna wyników pomiaru jest równa  V a odchylenie standardowe pojedynczego wyniku V. Z dokumentacji woltomierza wynika, że niedokładność pomiaru jest równa ±6⋅10^-4 wartości wskazanej oraz±2⋅10^-4 zakresu. Obliczyć całkowitą niepewność
pomiaru napięcia.

Niepewność standardowa wyniku pomiaru (w tym przypadku wynikiem jest średnia arytmetyczna z N obserwacji) ma dwie składowe:

a) składową związaną z zauważalnymi oddziaływaniami przypadkowymi wyrażaną odchyleniem standardowym średniej

 V,

Jest to standardowa niepewność bezwzględna typu A.

b) Składową związaną z niedokładnością przyrządu która nie jest podana za pomocą miar statystycznych. Sposób jej podania sugeruje iż suma podanych przez producenta przedziałów wyznacza całkowity przedział dopuszczalnych niepewności.

V

Usprawiedliwia to założenie o jednostajnym rozkładzie niepewności wewnątrz przedziału podanego przez producenta, a zatem obliczenie odchylenia standardowego wg zależności:

 V

Jest to standardowa niepewność bezwzględna typu B.

Całkowite odchylenie standardowe pomiaru jest równe

V

Jest to jednocześnie całkowita standardowa (P = 0,68) niepewność bezwzględna pomiaru.

Niepewność rozszerzona na poziomie ufności 99,73 % jest równa

 V

Ostateczny zapis:

 V; (poziom ufności 99,73 %)

Przykład 2

Na ramię o długości r = 1,0 m działa pod kątem prostym siła F = 1,05 N, wyznaczona z niepewnością standardową
. Obliczyć moment obrotowy i jego niepewność
.

Rozwiązanie

Ze wzoru na moment obrotowy obliczamy jego wartość

Ponieważ wyrażenie na M jest jednomianem algebraicznym, do obliczenia niepewności
stosujemy wzór (24):

Nieznana jest niepewność ramienia r. W celu jej wyznaczenia przyjmujemy, że wynik pomiaru r został prawidłowo zaokrąglony. Wówczas wartość rzeczywista r mieści w przedziale 0,95... 1,05 m, przy czym każda wartość r z tego przedziału jest jednakowo prawdopodobna. (rozkład jednostajny). Bezwzględną niepewność standardową
wyznaczamy zatem jako:

m

Względna niepewność standardowa
jest równa

Podstawiając do wzoru na
otrzymuje się

Bezwzględna niepewność standardowa momentu U_M jest równa

Ostateczny zapis:

 N⋅m; (poziom ufności 99,73 %)

6. Poszukiwanie zależności funkcyjnej opisującej ciąg wyników pomiarowych

Często występującym w praktyce inżynierskiej zagadnieniem jest poszukiwanie zależności funkcyjnej pomiędzy dwoma seriami wyników pomiaru obarczonych błędami przypadkowymi. Są to wyniki odpowiadające sobie parami , gdzie i = 1, 2 ... k. Rodzaj funkcji jest najczęściej znany lub domniemywany, przez co zagadnienie sprowadza się do znalezienia q współczynników (parametrów) a_j tej funkcji. Istnieją trzy przypadki:

k < q - zadanie jest nierozwiązalne (za mało danych);

k = q - przypadek matematycznie jednoznaczny, ale z metrologicznego punktu widzenia jest za mało danych, aby ocenić ich niepewność;

k > q - przypadek najczęściej występujący w metrologii.

Istnieje kilka metod wyznaczania charakterystyk. W każdej z nich wykorzystuje się tylko wartości poprawne wyników pomiarów.

Najprostszą metodą wyznaczenia charakterystyki jest metoda naciągniętej nici, nazywana metodą ”na oko”. Metoda ta może być stosowana, gdy szukana charakterystyka jest liniowa albo możliwe jest przekształcenie szukanej funkcji do postaci liniowej. Polega ona przedstawieniu wyników pomiaru w układzie współrzędnych prostokątnych, a następnie wykreśleniu takiej prostej, aby przechodziła przez największą liczbę punktów lub w ich pobliżu. Rozłożenie punktów wokół prostej powinno być w przybliżeniu symetryczne. Poszukiwane współczynniki wyznacza się ze współrzędnych dwóch punktów leżących na poszukiwanej prostej.

Najczęściej stosowaną i najbardziej ogólną metodą wyznaczania charakterystyk jest metoda najmniejszych kwadratów. Metoda ta polega na znalezieniu takich parametrów a_j funkcji, aby suma kwadratów różnic pomiędzy wynikiem y_i pomiaru a poszukiwaną funkcją była jak najmniejsza:

(dla wszystkich a_j , j = 1, 2 ... q) (30)

gdzie (31)

Liczba równań (32) jest równa liczbie poszukiwanych parametrów funkcji. Są to równania wzajemnie niezależne.

Tok obliczeń jest zalgorytmizowany dla typowych charakterystyk. Na przykład współczynniki szukanej zależności liniowej typu są dane równaniami

(32)

(33)

gdzie (34)

Na podstawie obliczonych współczynników ocenić można odchylenie standardowe  pojedynczego wyniku pomiaru y_i

(35)

Odchylenia standardowe obliczonych współczynników są równe

(36)

(37)

gdzie D jest dane wzorem (34).

Poszukiwanie równania charakterystyki liniowej jest nazywane regresją liniową. Zagadnienie poszukiwanie charakterystyki nieliniowej jest nazywane regresją nieliniową lub regresją wyższego rzędu. Metoda poszukiwania parametrów funkcji więcej niż jednej zmiennej (np. nosi nazwę regresji wielokrotnej.

Istnieje wiele programów komputerowych, które realizują metodę regresji. Ich stosowanie jest zalecane, gdyż obliczenia są z reguły dość żmudne.

Często charakterystyka wyznaczona doświadczalnie odbiega nieznacznie od liniowej. Dla scharakteryzowania tej rozbieżności wprowadzono pojęcie błędu nieliniowości . Do jego określenia pomocny jest rys.6.

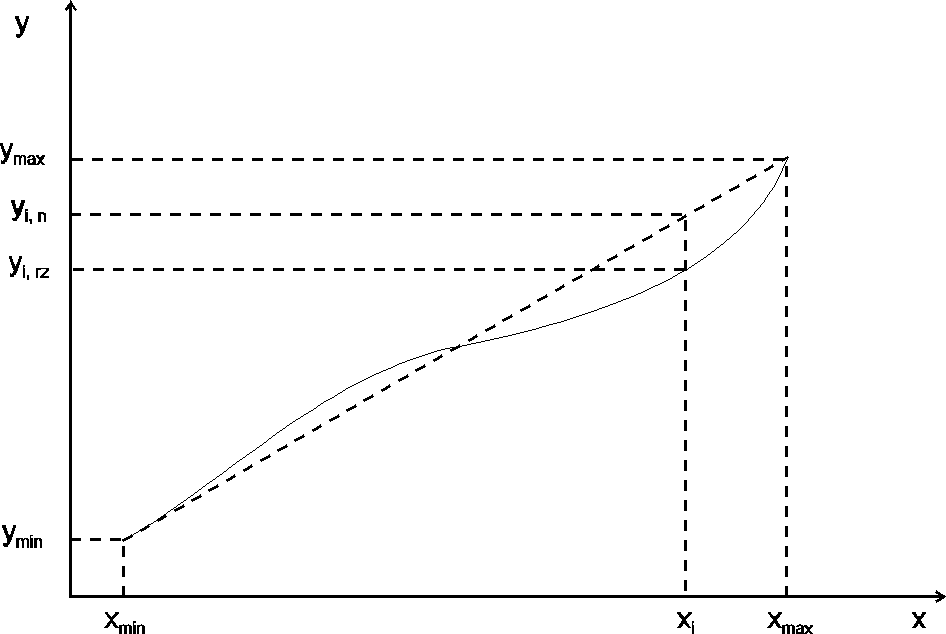
Rys.6 Do definicji błędu nieliniowości

Najczęściej błąd nieliniowości definiuje się następująco

(38)

7. Wykresy

Wykres jest graficznym sposobem przedstawienia wyniku pomiaru. Powinien on umożliwić łatwe zinterpretowanie otrzymanych wyników. Przykład poprawnie wykonanego wykresu przedstawiono na rys.7.

Rys.7 Przykład prawidłowo wykonanego wykresu

W przypadku, gdy wartości zmiennej którejś z osi zawierają się w przedziale większym od 1 dekady, to należy stosować skalę logarytmiczną. Należy zwrócić uwagę na to, że skali logarytmicznej nie można stosować w przypadku, gdy wartości zmiennej są mniejsze lub równe zeru.

8. Program ćwiczenia

a) wykonać serię n = 50 obserwacji okresu napięcia w sieci elektroenergetycznej. Pomiar wykonać wykorzystując tryb ręcznego wyzwalania okresomierza.

b) wykonać serię n = 50 obserwacji napięcia na wyjściu transformatora bezpieczeństwa. Pomiar wykonać wykorzystując tryb ręcznego wyzwalania woltomierza cyfrowego. Dokonać pomiaru temperatury otoczenia przed i po przeprowadzeniu doświadczenia.

c) zmierzyć wartość rezystancji rezystora metodą techniczną;

d) wykonać pomiar średnicy i wysokości mosiężnego wałka, wykorzystując do tego celu długościomierz cyfrowy i odpowiednią płytkę wzorcową. Pomiar wykonać w kilku punktach, starając się wyznaczyć przybliżony kształt wałka.

9. Opracowanie wyników pomiaru

- obliczyć i prawidłowo zapisać wyniki pomiarów przeprowadzonych w p. (a), (b) i (c). Wykorzystać dane zawarte w dokumentacji użytych przyrządów pomiarowych;

- obliczyć objętość wałka i prawidłowo zapisać wynik. Oszacować błąd modelowy i porównać z błędem instrumentalnym.

- znaleźć zależność funkcyjną dla danych pomiarowych wskazanych przez prowadzącego. Zbadać wpływ rzędu regresji na kształt poszukiwanej krzywej.

10. Pytania kontrolne

1) Podać definicję błędu bezwzględnego, poprawki i błędu względnego

2) Wyjaśnić różnicę między wartością rzeczywistą i poprawną

3) Podać znaczenie pojęć: niepewność typu A i niepewność typu B

4) Dlaczego do obliczeń niepewności używa się odchylenia standardowego ?

5) Dlaczego rozkład niepewności pomiaru ma z reguły charakter rozkładu normalnego?

6) Kiedy stosujemy rozkład t-Studenta?

7) Podać przykład zastosowania metody najmniejszych kwadratów

11. Literatura

1) Taylor J.R., Wstęp do analizy błędu pomiarowego, Wydawnictwo Naukowe PWN, Warszawa 1995

3) Zakrzewski J., Podstawy metrologii dla kierunku mechanicznego, Skrypt Pol. Śl. nr 1670, Gliwice 1991

4) Szydłowski H., Pracownia fizyczna, PWN, Warszawa 1994

5) Kubisa S., Podstawy metrologii, Skrypt Pol. Szczecińskiej, Szczecin 1995

6) Wyrażanie niepewności pomiaru. Przewodnik, Wydwnictwo GUM, Warszaw 1998.

Oprac. Marian Kampik, Jan Zakrzewski.

13

---