Politechnika Śląska w Katowicach.

Wydział Inżynierii Materiałowej i Metalurgii.

Modele tarcia i zjawisk cieplnych towarzyszących

procesom przeróbki plastycznej.

Michał Lis

M - 40 OPiCM

Tarciem nazywamy zjawisko powstawania oporu przy przesuwaniu się jednego ciała po powierzchni drugiego. Dla przezwyciężenia powstałego oporu konieczna jest określona siła, nazywana siłą tarcia.

W procesach przeróbki plastycznej występuje tarcie ślizgania, które znacznie różni się od tarcia ślizgania występującego w częściach maszyn (rys. 1.). Różnice te polegają na tym, że w przeróbce plastycznej na powierzchni tarcia działają wysokie naciski sięgające 2500 MN/m². W częściach maszyn występują naciski 10 ÷ 50 MN/m².

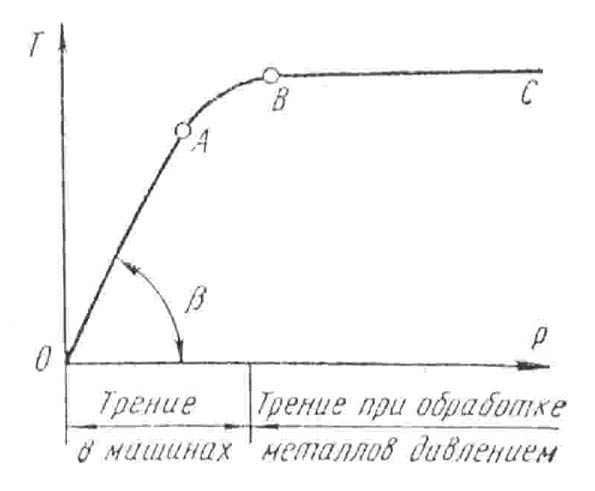
Rys. 1. Wpływ siły nacisku P na siłę tarcia T dla części

maszyn i w procesach przeróbki plastycznej.

Przemieszczanie cząstek metalu na powierzchni trących się części maszyn jest jednakowe we wszystkich punktach styku, podczas gdy w przeróbce plastycznej wielkość i prędkość przemieszczania jest różna w różnych punktach styku. Na przykład przy spęczaniu próbek cylindrycznych przemieszczanie metalu względem narzędzia jest w środku próbki równe zeru. W niektórych przypadkach ślizganie na powierzchni styku w ogóle nie występuje, pojawia się natomiast przyleganie. Odkształcenie w tym przypadku odbywa się przez przemieszczenia cząstek wewnątrz objętości ciała. Dla przeprowadzenia odkształcenia metalu w obecności tarcia należy przyłożyć siłę znacznie większą, niż to wynika z oporu plastycznego, jaki występuje w danych warunkach. Im większe jest tarcie, tym większa jest siła niezbędna dla odkształcenia i tym większe jest zużycie energii na odkształcenie. Tarcie jest jedną z przyczyn nierównomierności odkształcenia, która pogarsza jakość i własności metalu w całej jego objętości. Specjalnie duże zmiany można zauważyć w cienkich warstwach w pobliżu powierzchni zetknięcia metalu z narzędziem. Zmiana własności metalu odkształcanego zależy od prędkości i stopnia odkształcenia. Tarcie powoduje zużycie i nierównomierne wyrabianie narzędzi. Wady powierzchni narzędzi pozostawiają ślady na powierzchni odkształcanego ciała, pogarszając jego powierzchnię.

Wyróżnia się następujące mechanizmy tarcia:

1. Tarcie czyste występuje wtedy, gdy na powierzchni tarcia nie ma ani tlenków, ani smaru. Tarcie czyste może mieć więc miejsce tylko w warunkach doświadczalnych.

2. Tarcie suche występuje w przypadku, gdy na powierzchni styku metalu z narzędziem istnieją tlenki i zanieczyszczenia, nie ma natomiast smarów.

3. Tarcie płynne występuje wtedy, kiedy powierzchnie trących się ciał są w pełni izolowane warstewką smaru.

4. Tarcie półsuche występuje w takim przypadku, gdy na powierzchniach trących tylko niektóre powierzchnie oddzielone są lepkim ośrodkiem.

5. Tarcie półpłynne występuje, jeśli w obecności smaru istnieją bezpośrednie kontakty trących się ciał.

6. Tarcie graniczne występuje wtedy, kiedy warstwa ciekłego smaru rozdzielająca powierzchnie trące jest granicznie cienka, smar zaś jest powierzchniowo czynny.

W przeróbce plastycznej spotykamy się zazwyczaj z tarciem półsuchym lub półpłynnym. Mechanizm tarcia suchego, który jest zazwyczaj analogiczny do mechanizmu tarcia półsuchego, polega na zazębianiu się obu powierzchni. Wiadomo, że każda powierzchnia metalu ma nierówności, występy i wgłębienia, które powodują nadmierne zazębienie powierzchni trących. Faktyczna powierzchnia kontaktu jest w takich przypadkach mniejsza od teoretycznej powierzchni styku. W przeróbce plastycznej rzeczywista powierzchnia zwiększa się (rys. 2.).

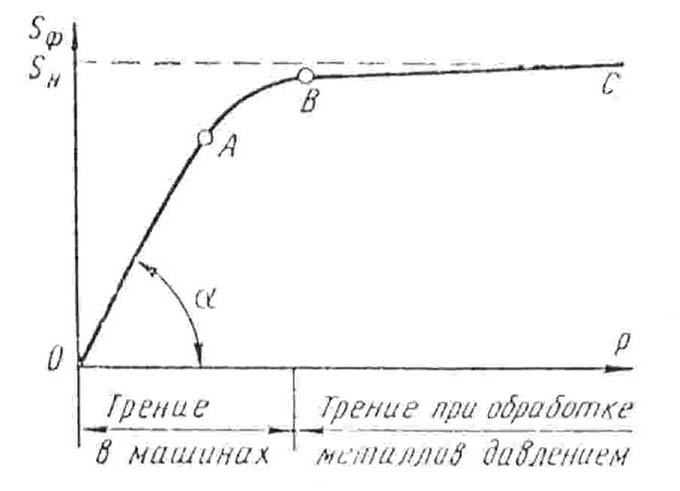
Rys. 2. Wpływ siły nacisku P na rzeczywistą powierzchnię styku S_

dla części maszyn i w procesach przeróbki plastycznej.

Aby przesunąć ciało w stosunku do drugiego (rys. 3.) należy przyłożyć siłę tarcia T, która według Amonton'a wynosi:

(1)

gdzie: f - współczynnik tarcia,

N - siła normalna.

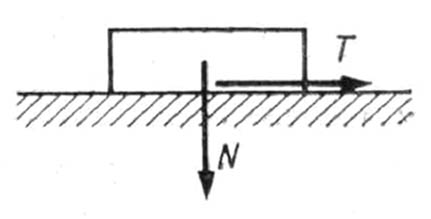
Rys. 3. Schemat sił występujących przy

ruchu ciała w obecności tarcia.

Ocenienie wartości siły i naprężenia tarcia na podstawie współczynnika tarcia nie jest w przeróbce plastycznej prawidłowe, ponieważ w tych obszarach powierzchni styku, w których znikają poślizgi, pojęcie współczynnika tarcia nie ma sensu fizycznego.

Epifanow definiuje siłę tarcia w następujący sposób:

(2)

gdzie: ₀ - styczne naprężenie ścinające w strefie przy kontaktowej,

S_k - powierzchnia zetknięcia metalu z narzędziem,

N - siła normalna,

- współczynnik uwzględniający prędkość zmiany.

Pierwszy człon równania (2) pokazuje zmianę siły tarcia wskutek zmiany powierzchni ścinania przy założeniu niezmienności wytrzymałości na ścinanie. Człon drugi przedstawia zmianę wytrzymałości na ścinanie przy zmianie normalnego nacisku. Dzieląc obie części wyrażenia (1) przez całkowitą powierzchnię kontaktu S mamy:

(3)

Wyrażenie T/S odpowiada średniemu naprężeniu tarcia , a N/S normalnemu naprężeniu σ₁. Zgodnie z tym:

(4)

Wzór (4) wyraża się następująco: naprężenie tarcia równe jest iloczynowi naprężenia normalnego i współczynnika tarcia. Jeśli naprężenie tarcia osiągnie wartość:

(5)

to prawdopodobieństwo poślizgu metalu po narzędziu lub wewnętrznego poślizgu w metalu będzie jednakowe. Przy zwiększeniu naprężenia normalnego σ₁ poślizg metalu po narzędziu zanika i następuje przyleganie, przy czym naprężenie tarcia nie zwiększa się. Przyleganie w tym przypadku nie może być utożsamiane z cząsteczkowym oddziaływaniem będących w kontakcie czystych powierzchni metalu. Do momentu występowania poślizgu obowiązuje zależność:

(6)

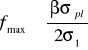
(7)

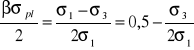
(8)

przy wszechstronnym ściskaniu (walcowaniu bez naciągów, spęczaniu, prasowaniu) σ₁ i σ₃ mają jednakowe znaki, a więc współczynnik tarcia:

(9)

Przy zróżnicowanym schemacie stanu naprężenia minimalne główne naprężenie normalne σ₃ jest mniejsze od zera i dlatego współczynnik tarcia może być większy od 0,5. Jednakże przy trójosiowym ściskaniu, np. przy walcowaniu i ściskaniu, doświadczalnie otrzymuje się współczynniki tarcia znacznie przewyższające 0,5. Można to wyjaśnić w ten sposób, że przy tych doświadczeniach współczynnik tarcia otrzymuje się jako iloraz średniego naprężenia tarcia przez nacisk jednostkowy. Działanie naprężenia tarcia w zasadzie lokalizuje się w pobliżu powierzchni styku i maksymalną jego wartość określa się podwyższonym oporem plastycznym σ_pl1, podczas gdy wielkość jednostkowego nacisku w całej objętości oznaczamy przez σ_1obj. Dlatego też maksymalny współczynnik tarcia wynosi:

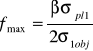
(10)

i może on być większy od 0,5 przy trójosiowym ściskaniu.

Stan powierzchni narzędzia (jego szorstkość) wpływa na naprężenie tarcia. Stan powierzchni narzędzia oceniamy jakością obróbki i jego zużycia w procesie eksploatacji. Gładkość powierzchni ocenia się jako średnią wartość pierwiastka kwadratowego z pomierzonych występów i wgłębień w mikrometrach.

Dla określenia klasy gładkości powierzchni stosuje się różnorakie przyrządy np. profilografy, profilometry i interferencyjne mikroskopy.

Wpływ temperatury przerabianego metalu na współczynnik tarcia jest złożony. Przy zmianie temperatury zmienia się opór plastyczny, zmieniają się również fizykochemiczne własności zgorzeliny, która tworzy pośrednią warstwę między metalem i narzędziem. Przy nagrzewaniu współczynnik tarcia początkowo zwiększa się, osiąga maksymalną wartość, następnie maleje (rys. 4.).

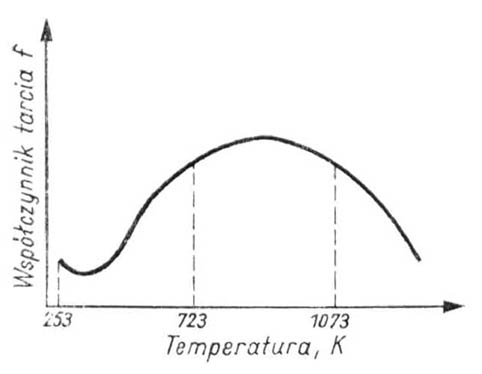
Rys. 4. Zależność współczynnika tarcia od temperatury

plastycznie przerabianego metalu.

Współczynnik tarcia zwiększa się początkowo w związku z utlenieniem powierzchni. W początkowym zakresie temperatur powstaje zgorzelina twarda zwiększająca współczynnik tarcia. Przy dalszym podwyższaniu temperatury następuje jej mięknięcie i zaczyna ona spełniać rolę smaru.

Ekelund na podstawie licznych eksperymentów ustanowił liniową zależność współczynnika tarcia od temperatury. Jest ona następująca:

(11)

gdzie: t - temperatura odkształcanego metalu,

k₁ - współczynnik uwzględniający materiał walców (żeliwne k₁ = 0,8; stalowe k₁ = 1,0),

k₂ - współczynnik uwzględniający prędkość walcowania,

k₃ - współczynnik uwzględniający rodzaj walcowanego materiału, a konkretnie jego strukturę (stal węglowa k₃ = 1,0; stal ledeburytyczna k₃ = 1,1; stal perlityczno - martenzytyczna k₃ = 1,3; stal austenityczna k₃ = 1,4; stal ferrytyczna k₃ = 1,55).

Współczynnik k₂ określany jest na podstawie wykresu (rys. 5.) podającego bezpośrednio zależność tego współczynnika od prędkości walcowania. Z wykresu wynika, że dla małych prędkości walcowania (ok. 2m/s) omawiany współczynnik wynosi k₂ = 1, a przy dużych prędkościach 0,4. W tym samym stopniu zmniejsza się współczynnik tarcia.

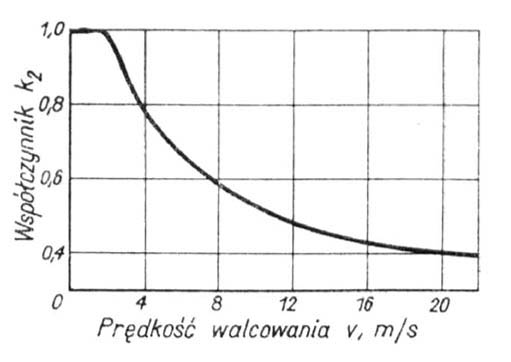
Rys. 5. Zależność współczynnika k₂

od prędkości walcowania.

W przeróbce plastycznej stosuje się szeroko smary, które zmniejszają współczynnik tarcia. Smar tworzy warstwę pomiędzy odkształcanym metalem i narzędziem izolując całkowicie lub częściowo jedno od drugiego. Jeśli smar w pełni oddziela obie trące powierzchnie, to wówczas mamy tarcie płynne. W przeróbce plastycznej, gdzie istnieją duże jednostkowe naciski, smar nie izoluje całkowicie obu trących powierzchni, w związku z czym mamy do czynienia z tarciem półpłynnym.

Przy tarciu płynnym rządzą inne prawa niż przy suchym. Siła tarcia niezbędna dla pokonania tarcia wewnętrznego warstwy smaru według Newtona wynosi:

(12)

a naprężenie tarcia:

(13)

gdzie: h - współczynnik lepkości dynamicznej,

v - prędkość poślizgu,

h - wysokość warstwy smaru.

Ze wzorów (12) i (13) widać, że siła i naprężenie tarcia przy tarciu płynnym nie zależą od nacisku normalnego, lecz w przeciwieństwie do tarcia suchego od powierzchni styku. Siła tarcia jest tym większa, im większa jest lepkość smaru. Im większy nacisk jednostkowy na powierzchni styku, tym większą lepkość powinien mieć smar. Wpływ prędkości poślizgu przy tarciu płynnym jest przeciwny niż przy tarciu suchym. Przy tarciu suchym siła tarcia maleje wraz ze zwiększeniem się prędkości poślizgu, natomiast przy płynnym odwrotnie. Jednakże przy zwiększaniu prędkości poślizgu, większa ilość smaru dostaje się do strefy odkształcenia, grubość warstwy zwiększa się i siła tarcia maleje.

W zależności od warunków stosuje się następujące smary:

1. Smary płynne - np. emulsje, oleje roślinne i mineralne.

2. Smary proszkowe - są to przeważnie mydła w postaci proszków lub płatków oraz grafit.

3. Szkło - w postaci proszku lub waty szklanej.

Całkowita praca związana z odkształceniem plastycznym metalu wynosi:

(14)

W zależności od warunków odkształcenia, część pracy odkształcenia plastycznego zostaje zamieniona na ciepło zgodnie z bilansem energii.

---