Tytus Sosnowski

Kurs 004 (2008 / 2009)

METODOLOGIA BADAŃ PSYCHOLOGICZNYCH

Wykład obligatoryjny dla I roku studiów wieczorowych

Wydziału Psychologii UW

PLANOWANIE I ANALIZA BADAŃ EMPIRYCZNYCH

Część C:

plany eksperymentalne

PRZEGLĄD TYPOWYCH PLANÓW EKSPERYMENTALNYCH

1. Plany w grupach kompletnie zrandomizowanych.

1.1. Plany jednoczynnikowe (jedna zmienna niezależna).

1.1.1. dwa poziomy zmiennej niezależnej;

1.1.2. wiele poziomów zmiennej niezależnej.

1.2. Plany wieloczynnikowe (wiele zmiennych
niezależnych): oddziaływania addytywne i
interakcja.

2. Plany z powtarzanymi pomiarami.

3. Plany oparte na kwadracie łacińskim.

4. Plany w blokach kompletnie zrandomizowanych.

5. Analiza kowariancji.

W analizie wariancji (ANOVA) zmienne niezależne nazywane są czynnikami (stąd: plany jednoczynnikowe, dwuczynnikowe, itp.) W ANOVA mamy zawsze jedną zmienną zależną (tzw. analiza jednozmiennowa, univariate). Jeśli zmiennych zależnych jest więcej przeprowadzamy dla każdej z nich oddzielną (jednozmiennową) analizę.

1. Plany w grupach kompletnie zrandomizowanych

1.1.1 Plany jednoczynnikowe, dwugrupowe
(dwa poziomy zmiennej niezależnej

Tabela 5c.1. Klasyczny eksperyment dwugrupowy

Grupy zrandomizowane: G1 G2

zmienna niezależna (X): X1 X2

zmienna zależna (Y):

Stosując analizę wariancji otrzymujemy test F jako oszacowanie istotności różnicy między średnimi
i
,
Przy dwóch grupach możemy też zastosować test t-studenta (dla dwu grup: F = t² ).

Zakładamy, że (dzięki randomizacji) grupy eksperymentalne nie różniły się między sobą przed eksperymentem. Jeśli mamy co do tego wątpliwości, możemy zastosować pomiar początkowy (por. plan Solomona)

Jeśli nie było różnic między grupami przed eksperymentem, a pojawiły się po zastosowaniu manipulacji zmienną X, to mamy prawo wnioskować że X wpływa na Y (działanie zmiennej X jest przyczyną zmian zmiennej Y).

Tabela 5c.2. Czterogrupowy plan Solomona

Grupy	Pomiar Oddziały- Pomiar początkowy wanie końcowy
G 1: Kontrolna	---- ---- Yk1
G 2: Kontrolna	Yp2 ---- Yk2
G 3: Eksperymentalna	---- X Yk3
G 4: Eksperymentalna	Yp4 X Yk4

Plan ten pozwala ocenić efektywność randomizacji oraz wpływ pomiaru początkowego i zmiennej głównej (X) na pomiar końcowy (Y).

Oszacowania efektu zmiennej X i pomiaru początkowego dokonujemy przez PORÓWNANIE POMIARÓW KOŃCOWYCH. Porównania między pomiarami początkowymi i końcowymi mają znaczenie pomocnicze gdyż nie gwarantują takiej kontroli zmiennych ubocznych jak porównania między grupami zrandomizowanymi.

Zachowanie badacza może być stronnicze. Aby wyeliminować ten efekt i efekt placebo, stosuje się tzw. plan eksperymentalny ślepy (single-blind), w którym osoby badane nie mają dostępu do informacji mogących wpłynąć na wynik badania (np. do informacji, która grupa jest kontrolna a która eksperymentalna), plan podwójnie ślepy (double-blind), w którym informacje takie są niedostępne dla eksperymentatora (osoby kontaktującej się z badanymi), lub nawet potrójnie ślepy (triple-blind), w którym informacje te są niedostępne dla osoby analizującej wyniki.

1.1.2. Plany jednoczynnikowe wielogrupowe
(wiele poziomów zmiennej niezależnej)

Tabela 5c.3. Eksperyment jednoczynnikowy, czterogrupowy

Grupy zrandomizowane: G1 G2 G3 G4

zmienna niezależna (X): X1 X2 X3 X4

zmienna zależna (Y):

Wielokrotne porównania między średnimi

Zbiorczy test F (omnibus F test) dla jednoczynnikowego planu wielogrupowego testuje hipotezę zerową:
H₀: μ₁ = μ₂ = μ₃ = ... μ_n.

Jeśli uda się odrzucić tę hipotezę (F okaże się istotne) to nie wiemy, które średnie różnią się miedzy sobą a które nie. Do analizy różnic między poszczególnymi średnimi (grupami, pomiarami) służy analiza kontrastów.

Kontrasty post hoc (a posteriori)

Stosuje się je wówczas, gdy badacz nie ma jasnej hipotezy co kierunku zależności miedzy zmiennymi. Szacujemy wówczas istotność różnic między wszystkimi możliwymi parami średnich (multiple comparisons). Do porównań takich nie należy używać tradycyjnego testu t Studenta, ale specjalnych testów (kontrastów post hoc), takich np. jak:

• test Tukeya

• test Duncana

• test Scheffego (najbardziej konserwatywny test post hoc)

Procedura Bonferroniego

Do wielokrotnych porównań między parami średnich (dla danych skorelowanych jak i nieskorelowanych) można zastosować test t Studenta z tzw. poprawką Bonferroniego.

Poprawka ta polega na tym, że wartość p dla tradycyjnego testu t Studenta (wyszukaną w tablicach, lub podaną przez komputerowy program statystyczny) mnożymy przez liczbę dokonywanych porównań między średnimi.

Przykład

Mamy pięć średnich i dokonujemy czterech porównań (każdą z czterech pierwszych średnich porównujemy z ostatnią). Dla różnicy między średnimi M₁ i M₅ otrzymaliśmy t(30) = 2,80, p < 0,01. Istotność testu t z poprawką Bonferroniego wynosi: 0,01 x 4 = 0,04 (≈ 0,05).

Procedura Bonferroniego jest łatwa w stosowaniu ale bardzo konserwatywna (różnice oszacowane innymi metodami jako istotne, mogą okazać się nieistotne przy zastosowaniu metody Bonferroniego), szczególnie gdy liczba porównań jest duża.

Wady wielokrotnych porównań między średnimi.

• Jeśli porównujemy ze sobą wszystkie średnie, to liczba możliwych porównań bardzo szybko rośnie ze wzrostem liczby średnich. Liczba takich porównań wynosi:
  k (k-1)/2 (gdzie k = liczba średnich). Np. dla 5 średnich mamy 5(5-1)/2 = 10 porównań.
  

• Jeśli porównujemy parami dużą liczbę średnich, otrzymujemy w wyniku mało przejrzysty i trudny do interpretacji obraz zależności między zmiennymi.
  

Kontrasty planowane (a priori)

(w SPSS jako: kontrasty)

Kontrasty planowane (inaczej a priori) przeznaczone są do testowania istotności tylko wybranych różnic między średnimi, tych mianowicie, o których mowa w hipotezie (hipotezach) teoretycznych.

Jeśli liczba średnich równa się k, to możemy poddać analizie nie więcej niż k-1 kontrastów planowanych. Na przykład, dla 6 średnich mamy 15 możliwych kontrastów post hoc, ale nie więcej niż 5 kontrastów planowanych.

Kontrasty planowane mają większą moc niż kontrasty
post hoc: ta sama różnica miedzy średnimi może się okazać istotna, jeśli jest analizowana jako kontrast planowany, a nieistotna - jeśli jest analizowana jako kontrast post hoc. Przy kontrastach post hoc liczba porównań jest większa, więc i prawdopodobieństwo losowego pojawienia się dużej różnicy miedzy średnimi jest większe. Testy post hoc zawierają „poprawkę” na taki efekt.

w SPSS można wybrać z menu gotowe (już zdefiniowane) kontrasty planowane lub samodzielnie je zdefiniować używając odpowiednich współczynników (por. następna strona).

Jeśli analizujemy kontrasty planowane, nie musimy liczyć ogólnego testu F.

Przykłady kontrastów

Po lewej stronie podano przykładowe hipotezy dotyczące różnic miedzy grupami (A, B, C, itd.), po prawej - współczynniki kontrastów zdefiniowanych tak aby sprawdzić te hipotezy. Suma współczynników dla każdego kontrastu musi równać się zero.

1) Współczynniki dla kontrastów prostych (każdą grupę porównujemy z grupą odniesienia; tu - z grupą D):

A > D ψ₁: 1, 0, 0, -1; suma = 0

B > D ψ₂: 0, 1, 0, -1; suma = 0

C > D ψ₃: 0, 0, 1, -1; suma = 0

2) Współczynniki dla kontrastów zdefiniowanych
po lewej stronie:

A = B ψ₁: 1, -1, 0, 0; suma = 0

C = D ψ₂: 0, 0, 1, -1; suma = 0

(A+B) > (C+D) ψ₃: 1, 1, -1, -1; suma = 0

3) Współczynniki dla kontrastów zdefiniowanych
po lewej stronie:

A > B,C ψ₁: 2, -1, -1; suma = 0

B = C ψ₂: 0, 1, -1; suma = 0

Wśród kontrastów planowanych wyróżnia się tzw. kontrasty ortogonalne. Dla kontrastów ortogonalnych (i tylko dla nich) zachodzi równość:

SS_ψ1 + SS_ψ2 + ... SS_ψn = SS_czynnik

Dwa kontrasty są ortogonalne jeśli suma iloczynów ich współczynników (suma iloczynów współczynników przypisanych tym samym grupom) równa się zero, np.:

ψ₁: 2, -1, -1; suma = 0

ψ₂: 0, 1, -1; suma = 0

Suma iloczynów (0) + (-1) + (1) = 0

Jeśli liczba kontrastów > 2, to suma iloczynów ich współczynników musi równać się zero dla każdej pary kontrastów.

Zauważ, że kontrasty proste, podane wyżej, nie są ortogonalne.

Analiza trendów (wielomianowych)

(w SPSS jako: kontrasty > wielomianowe)

Trendy wielomianowe są szczególnym przypadkiem kontrastów ortogonalnych. Analiza trendów ma na celu oszacowanie, czy zależność między zmiennymi (niezależną i zależną) da się przybliżyć za pomocą wielomianu n-tego stopnia, a graficznie - przedstawić jako linia prosta (trend liniowy) lub jakaś linia krzywa (trend krzywoliniowy).

Analiza trendów wymaga aby zmienna niezależna była ciągła, mierzona na skali interwałowej, a jej kolejne, dyskretne wartości (zastosowane w badaniu) były rozłożone w równych odstępach. Do analizy trendów można stosować zarówno ANOVA-ę jak i analizę regresji wielokrotnej.

• Ilustrację graficzną wielomianu n-tego stopnia stanowi linia (łącząca średnie) mająca n-1 zgięć (tzn. n-1 razy zmieniająca kierunek, por rycina 1 i 2). Na przykład, ilustracją trendu stopnia drugiego („kwadratowego”) jest linia zmieniająca jeden raz swój kierunek.
  

• Dla wykrycia trendu n-tego stopnia potrzeba co najmniej n+1 średnich (grup). Np. aby wykryć trend 2-go stopnia potrzebne są co najmniej trzy średnie.
  

• Znalezienie istotnego trendu, dobrze dopasowanego do danych, może wskazywać na istnienie ogólnej zależności między zmiennymi.
  

Rycina 1a. Przykładowe dane

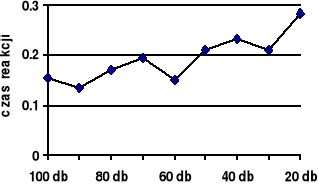
Rycina 1b. Trend liniowy

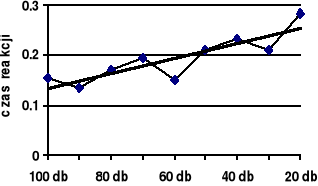
Rycina 2a. Przykładowe dane

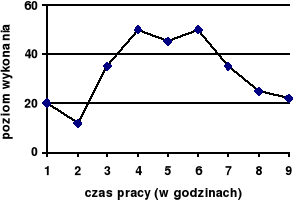
Rycina 2b. Trend kwadratowy (2-go stopnia)

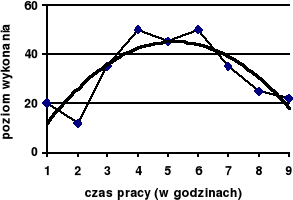
Ocena wielkości (siły) efektu

(effect size)

Czym innym jest pytanie o to, czy różnica między średnimi w ogóle istnieje (istotność różnicy) a czym innym pytanie o to, ja duża jest ta różnica (wielkość efektu). Na przykład, dysponując precyzyjną wagę laboratoryjną możemy wykazać że waga dwóch przedmiotów różni się o 10 mg, a dysponując tylko wagą towarową możemy nie być w stanie wykazać, że waga dwóch ciężarówek różni się o 10 kg.

Istotność testu statystycznego zależy od wielkości próby. Nawet niewielka różnica między średnimi będzie istotna jeśli próba będzie bardzo duża, a duża różnica między średnimi może okazać się nieistotna gdy próba będzie bardzo mała. Istotność różnicy nie wskazuje więc, czy różnica ta jest mała czy duża. Ogólnie: istotność statystyczna efektu nie wskazuje czy jest on silny czy słaby. Dziś coraz częściej wymaga się aby podawać nie tylko istotność efektu ale i jego wielkość.

W analizie regresji miarą siły efektu zm. niezależnej (lub zmiennych niezależnych w regresji wielokrotnej) jest współczynnik determinacji, tzn. kwadrat współczynnika korelacji: r² lub R² . Jeśli np. R² = 0,40 to znaczy to, że 40% sumy kwadratów zmiennej zależnej można przewidzieć na podstawie znajomości zmiennych niezależnych

W ANOVA można stosować różne miary siły wpływu czynnika eksperymentalnego. Jedną z najlepszych jest współczynnik ω² („omega kwadrat”). Na przykład, w eksperymencie jednoczynnikowym, siłę wpływu czynnika A można policzyć wg wzoru::

Wzory na ω² dla innych planów eksperymentalnych podaje Brzeziński („Badania eksperymentalne w psychologii i pedagogice”, Warszawa: Scholar, 2000).

W menu programu SPSS nie ma współczynnika ω², jest natomiast współczynnik η² (eta kwadrat), który interpretuje się podobnie jak ω², tzn. jako procent zmienności (sumy kwadratów) zmiennej zależnej, wywołanej wpływem czynnika eksperymentalnego. Jeśli np. w eksperymencie
η² = 0,20 dla czynnika A, to znaczy to, że 20% zmienności zmiennej zależnej wywołana została działaniem czynnika A.

Najprostsza wersja współczynnika η² ma postać:

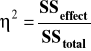
Inna wersja wzoru (dostępna w SPSS) ma postać:

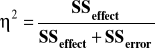
(w wypadku eksperymentu jednoczynnikowego oba wzory dają ten sam wynik).

Współczynnik η² (w wersji dostępnej w SPSS) można stosować do porównywania efektu tej samej zmiennej w różnych badaniach. Jeśli natomiast oceniamy efekty różnych czynników w tym samym eksperymencie to może się okazać, że suma wszystkich η² (tzn. oszacowanych dla wszystkich czynników eksperymentalnych) będzie większa od 1.

Przykład:

CUD - efekt Poffenbergera (1912)

(por. Wolski 2005)

Ruch prawej ręki kontroluje lewa półkula mózgu, ruch lewej ręki - prawa półkula. Czas reakcji motorycznej jest krótszy jeśli bodziec wzrokowy eksponowany jest do tej samej półkuli, która kontroluje ruch reagującej ręki niż wtedy, gdy jest kierowany do półkuli przeciwnej (bodziec eksponuje się w taki sposób aby trafiał tylko do jednej, wybranej połowy pola widzenia). Średnia różnica między czasem prostej reakcji skrzyżowanej i nieskrzyżowanej (crossed-uncrossed difference - CUD) miała wynosić wg Poffenbergera 4 milisekundy, dziś szacuje się ją na 3 ms.

CUD jest efektem bardzo słabym. Aby wykazać jego istotność statystyczną potrzeba wielkiej liczby (kilkuset ) prób. Wolski w swoich badaniach (eksperyment 2001, 2003) stosował 6 sesji po 240 prób (ekspozycji bodźców) w każdej sesji, czyli: 6 x 240 = 1440 prób dla każdej z około 40 osób badanych.

1.2. Plany wieloczynnikowe w grupach kompletnie zrandomizowanych

Tabela 5c.4. Schemat eksperymentu: AxB (2 x 2)

	B1	B2
A1	A1B1	A1B2
A2	A2B2	A2B2

SS_c = SS_mg + SS_wg

SS_mg = SS_A + SS_B + SS_AxB

Dzieląc sumy kwadratów przez stopnie swobody otrzymamy następujące oszacowania wariancji:

MS_mg (MS_A; MS_B; MS_AxB) i MS_wg

Dzieląc MS dla efektów przez MSwg trzymamy odpowiednie testy F:

- dla różnic między grupami: F = MS_mg / MS_wg

- dla czynnika A: F = MS_A / MS_wg

- dla czynnika B: F = MS_B / MS_wg

- dla interakcji A x B: F = MS_AxB / MS_wg

ODDZIAŁYWANIA ADDYTYWNE i INTERAKCJA:

EFEKTY GŁÓWNE I EFEKTY PROSTE

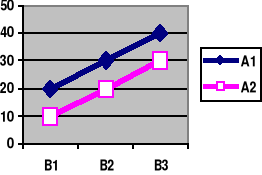
Przykład planu eksperymentalnego A x B (2 x 3)

1) Brak interakcji 2) Interakcja

	B1	B2	B3	Mw
A1	20	30	40	30
A2	10	20	30	20
Mk	15	25	35	25
	B1	B2	B3	Mw
A1	10	30	50	30
A2	10	20	30	20
Mk	10	25	40	25

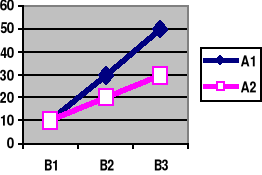
Efekt główny i efekt prosty mogą być różne definiowane, zależnie od metody analizy. Najprościej można je zdefiniować jako różnice między dwiema średnimi.

Efekt GŁÓWNY (main effect) danej zmiennej to różnica między jej wartościami brzegowymi w tabeli (zacienionymi).

Ogólnie - jest to efekt danej zmiennej uśredniony po wszystkich poziomach drugiej zmiennej (np. efekt zmiennej

A uśredniony po wszystkich poziomach zmiennej B).

Efekt PROSTY (simple effect) danej zmiennej to różnica między jej wartościami w polach tabeli (niezacienionymi).
Ogólnie - jest to efekt jednej zmiennej zachodzący dla wybranego poziomu drugiej zmiennej (np. efekt zmiennej A zachodzący dla B1, B2, itd.). Efekt prosty nazywany jest też efektem warunkowym (A/B1, A/B2, A/B3 lub B/A1, B/A2).

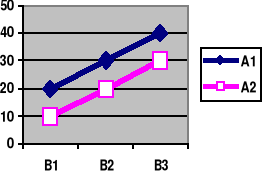
Jeśli wszystkie efekty proste są sobie równe (a tym samym są równe efektowi głównemu) to nie ma interakcji (linie łączące średnie są wtedy równoległe). Przykładowo, w Tab. 1 efekty proste zmiennej A są sobie równe: α₁ = α₂ = α₃ (= α.).

Liczbowo wynosi to: (20 - 10) = (30 - 20) = (40 - 30)

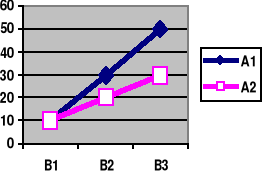
W Tabeli. 2 efekty proste nie są równe: α₁ ≠ α₂ ≠ α₃, (a linie łączące średnie nie są równoległe), co łatwo sprawdzić.

Czynniki eksperymentalne pozostają w INTERAKCJI jeśli efekt jednego czynnika na zmienną zależną zależy od poziomu innego czynnika. Nie analizujemy wtedy efektów głównych, tylko efekty PROSTE.

Jeśli wpływ jednego czynnika nie zależy od poziomu drugiego czynnika, to nie zachodzi interakcja. Analizujemy wówczas tylko efekty GLÓWNE.

Przy braku interakcji łączny efekt obu zmiennych jest sumą ich efektów głównych (efekty te są ADDYTYWNE):

SS_mz = SS_A + SS_B

Jeśli zachodzi interakcja, w równaniu pojawia się dodatkowy czynnik:

SS_mz = SS_A + SS_B + SS_AxB

Jeśli nie ma interakcji, wyniki eksperymentu
n-czynnikowego są równoważne wynikom n eksperymentów jednoczynnikowych. Jeśli zachodzi interakcja, konieczny jest eksperyment wieloczynnikowy.

ANALIZA WARIANCJI 2 X 3

(przykład liczbowy SPSS)

anova Z by A (1,3) B (1,2) / statistics=3.

* * * C E L L M E A N S * * *

B 1 2

A 1 6.00 6.00

2 6.00 10.00

3 6.00 14.00

* * * A N A L Y S I S O F V A R I A N C E * * *

Sum of Mean Signif.

Source of Variation Squares DF Square F of F

Main Effects 80.000 3 26.667 10.000 .009

A 32.000 2 16.000 6.000 .037

B 48.000 1 48.000 18.000 .005

2-way Interactions 32.000 2 16.000 6.000 .037

A x B 32.000 2 16.000 6.000 .037

Explained 112.000 5 22.400 8.400 .011

Residual 16.000 6 2.667

Total 128.000 11 11.636

---------------------------------------------------------------------------

Graficzna prezentacja efektów głównych i interakcji

Rycina 3a. Efekty główne czynnika A (trudność zadania)
i czynnika B (nagroda)

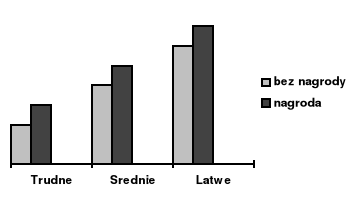
Rycina 3b. Efekty główne czynnika A (trudność zadania)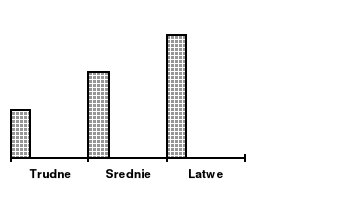

Rycina 3c. Efekty główne czynnika B (nagroda)

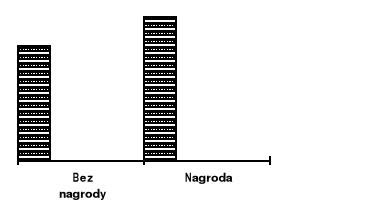
Rycina 4a. Interakcja czynników A i B (ilustracja danych
z wydruku SPSS)

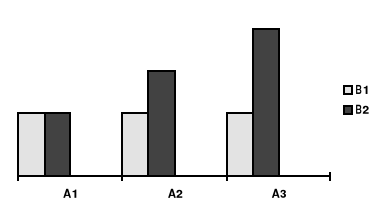
Rycina 4b. Interakcja czynników A i B

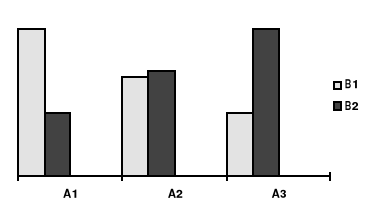
Rycina 4c. Interakcja czynników A i B

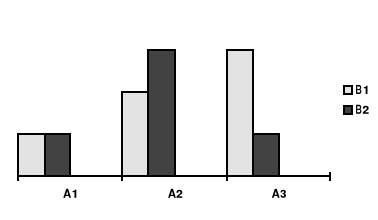
Interakcja zmiennej kategorialnej i ciągłej

Przykład: wpływ poziomu reaktywności (X1) i sytuacji stresowej (X2) na wielkość reakcji na stres (Y).

Miarą wpływu reaktywności (zmienna ciągła) jest nachylenie linii regresji; miarą wpływu sytuacji stresowej (zmienna kategorialna) jest różnica między liniami regresji dla obu grup.

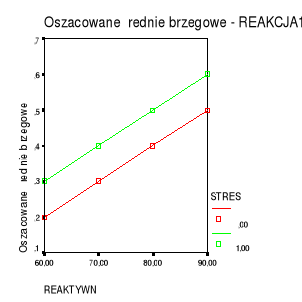
Rysunek 1a. Brak interakcji.

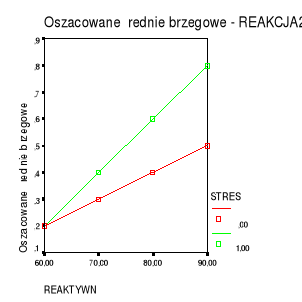
Rysunek 1b. Interakcja

Interakcja zmiennych ciągłych

Przykład: Wpływ dwóch mierzonych zmiennych niezależnych (plan ex-post facto): inteligencji (V1)
i poziomu motywacji (V2) na poziom wykonania zadań umysłowych (V3).

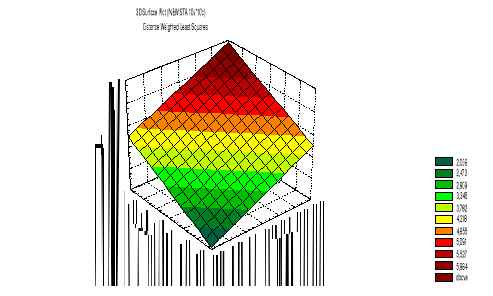
Brak interakcji: Wpływ jednej zmiennej niezależnej nie zależy od poziomu drugiej zmiennej. Inaczej - nachylenie linii regresji V3 względem V1 jest takie same dla wszystkich wartości V2, a nachylenie regresji V3 względem V2 jest takie same dla wszystkich wartości V1.

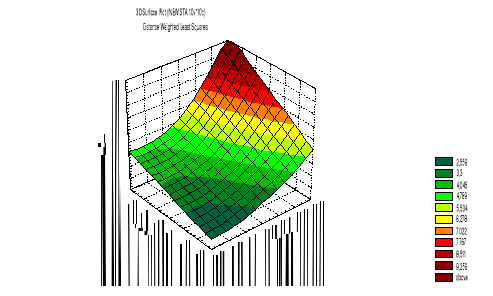
Interakcja: Wpływ jednej zmiennej niezależnej zależy od poziomu drugiej zmiennej. Inaczej - nachylenie linii regresji V3 względem V1 jest różne dla różnych wartości X2 lub nachylenie regresji V3 względem V2 jest różne dla różnych wszystkich wartości V1.

2. Plany z powtarzanymi pomiarami

Plan w grupach zrandomizowanych - na każdej osobie dokonujemy JEDNEGO pomiaru zmiennej zależnej.

Plan z powtarzanymi pomiarami - na każdej osobie dokonujemy KILKU (co najmniej dwóch) pomiarów zmiennej zależnej.

Tabela 5c.5a. Plan jednoczynnikowy w grupach kompletnie
zrandomizowanych

Zm. Niezależna (A): A1 A2 A3

Grupy: gr 1 gr 2 gr 3

Tabela 5c.5b. Plan jednogrupowy z powtarzanymi
pomiarami.

Zm. Niezależna (A): A1 A2 A3

Pomiary (ta sama grupa): pom 1 pom 2 pom 3

Tabela 5c.6. Plan jednoczynnikowy, dwugrupowy (grupy
zrandomizowane) z powtarzanymi pomiarami.

Pomiar zmiennej zależnej Y	Y1	Y2	Y3
Grupa 1 (X1)	Y11	Y12	Y13
Grupa 2 (X2)	Y21	Y22	Y23

Np. Sprawdzamy jak długo trwają efekty leku (X1)
w porównaniu do placebo (X2). Efekt działania leku mierzymy trzykrotnie (Y1, Y2, Y3), np. co godzinę.

Oszacowania efektów manipulacji dokonujemy przez PORÓWNANIE MIĘDZY GRUPAMI.

Stosowanie powtarzanych pomiarów NIE JEST MANIPULACJĄ EKSPERYMENTALNĄ !!!

Porównania między pomiarami nie zapewniają takiej kontroli zmiennych ubocznych jak porównania między grupami zrandomizowanymi.

Dlatego wnioski oparte na podstawie porównań między pomiarami są mniej wiarygodne niż wnioski oparte na porównaniach międzygrupowych.

Zalety i wady planów z powtarzanymi pomiarami

Zalety

• Są bardziej ekonomiczne (mniej badanych osób).

• Łatwiej uzyskać wysoką wartość testu F, gdyż możemy wyłączyć z wariancji błędu różnice między osobami.

• Niektóre problemy wymagają stosowania powtarzanych pomiarów, np. badanie habituacji, reminiscencji (zjawisko Ballarda). Ma to miejsce najczęściej wtedy, gdy badane zjawisko polega na zmianach w czasie.

Wady

• Silniejsze (trudniejsze do spełnienia) założenia modelu statystycznego;

• Słabsza (niż w wypadku planów w grupach zrandomizowanych) kontrola zmiennych ubocznych.
  

Jednym z problemów jest kontrola kolejności poziomów zmiennej niezależnej. Jeśli poziomy zmiennej niezależnej eksponowane są w stałej kolejności trzeba się liczyć z:

* wpływem czynników działających w czasie trwania pomiaru (np. habituacja, zmęczenie)

* wpływem wcześniejszych pomiarów na pomiary późniejsze
(np. uczenie się, zmiana nastawienia do badania).

* niektóre zmienne niezależne mogą wykluczać (lub
ograniczać) stosowanie powtarzanych pomiarów
(por. klasyczne eksperymenty z manipulacją
wiarygodnością informatora).

3. Plany oparte na kwadracie łacińskim

Załóżmy, że w eksperymencie z powtarzanymi pomiarami zmienną niezależną jest rodzaj zadania. Stosujemy trzy rodzaje zadań (A, B, C) i chcemy wykluczyć wpływ kolejności rozwiązywania zadań na zmienną zależną.

Tabela 5c.7. Plan oparty na permutacji elementów

Osoba badana (grupa osób) próba 1 próba 2 próba 3

1 A B C

2 A C B

3 B A C

4 B C A

4 C A B

6 C B A

Przy sześciu osobach badanych, każda z nich wykonuje zadania w innej kolejności. Możemy też przebadać większą liczbę osób (tzn. wielokrotność liczby 6).

Wadą schematu z tabeli 5c-7 jest to, że liczba permutacji rośnie bardzo szybko z liczbą elementów permutowanych.

n liczba permutacji (n!)

3 6

5 120

10 3 628 800

KWADRAT ŁACIŃSKI*

Kwadrat łaciński pozwala planować badania z dużą liczbą poziomów zmiennej niezależnej a jednocześnie małą liczbą badanych osób.

Tabela 5c.8. Plan trójczynnikowy (osoby x próby x zadania) oparty na kwadracie łacińskim 4 x 4. Kontrolujemy kolejność czterech zadań (A, B, C, D) badając tylko cztery osoby (lub wielokrotność tej liczby).

Osoba badana (grupa osób)	próba 1	próba 2	próba 3	próba 4
1	A	B	C	D
2	B	C	D	A
3	C	D	A	B
4	D	A	B	C

* Nazwa "łaciński" pochodzi liter alfabetu łacińskiego
którymi oznacza się pola kwadratu.

Jak widać:

• Każde zadanie występuje tylko raz w każdym wierszu (osoba badana) i każdej kolumnie (próba).

• Każdy poziom każdego czynnika spotyka się dokładnie jeden raz z każdym z poziomów każdego innego czynnika.

• Każda ze zmiennych musi mieć taką samą liczbę poziomów, równą wymiarowi kwadratu. Gdyby liczba zadań wynosiła przykładowo 10, kwadrat (10 x 10) musiałby mieć 10 wierszy (osób) i 10 kolumn (prób).

W kwadrat łaciński można wbudować dodatkową, czwartą zmienną (a nawet więcej zmiennych). Przy czterech zmiennych otrzymujemy tzw. kwadrat "grecko-łaciński"
(od liter alfabetu greckiego i łacińskiego).

Tabela 5c.9. Kwadrat grecko-łaciński,

czteroczynnikowy, „4 x 4”

	K1	K2	K3	K4
W1	A α	B β	C γ	D δ
W2	B γ	A δ	D α	C β
W3	C δ	D γ	A β	B α
W4	D β	C α	B δ	A γ

Kwadraty łacińskie, o wymiarach od „3 x 3” do „12 x 12” można znaleźć w pracy:

Ryszard Zieliński (1972). Tablice statystyczne (tablica 57
i 58). Warszawa: PWN.

4. Plany w blokach kompletnie zrandomizowanych.

Randomizacja zapewnia kontrolę zmiennych ubocznych w tym sensie, że zmienne te działają we wszystkich grupach tak samo (rozkład zmiennej zależnej powinien być taki sam we wszystkich grupach).

Randomizacja nie ma jednak wpływu na WIELKOŚĆ wariancji w zbiorach (wariancji niekontrolowanej). W przypadku porównań międzygrupowych ważnym źródłem wariancji wewnątrz-grupowej są różnice indywidualne.

Plan w BLOKACH kompletnie ZRANDOMIZOWANYCH polega na tym, że wybraną zmienną indywidualną czynimy zmienną eksperymentalną (kontrolowalną). Tym samym minimalizujemy wielkość wariancji niekontrolowanej (wewnątrzgrupowej).

Tabela 5c.-10. Plan w blokach kompletnie zrandomizowanych.

Zmienna blokowa (I.I.) Zmienna manipulowalna Bloki grupa 1 grupa 2

blok 1 ( 78 < II < 82) 11 21

blok 2 ( 88 < II < 92) 12 22

blok 3 ( 98 < II < 102) 13 23

blok 4 (108 < II < 112) 14 24

blok 5 (118 < II < 122) 15 25

Y - wynik pomiaru zmiennej zależnejPlan w blokach kompletnie zrandomizowanych:

Sposób doboru osób do grup eksperymentalnych

• Najpierw dobieramy osoby w bloki pod względem wybranej zmiennej indywidualnej (blokowej). Następnie przydzielamy losowo (randomizacja) osoby z każdego bloku do grup eksperymentalnych.

• Osoby w tym samym bloku powinny być jak najbardziej podobne do siebie pod względem zmiennej blokowej, natomiast osoby w różnych blokach - jak najbardziej różnić się od siebie.

Schemat blokowy pozwala:

• ocenić siłę wpływu wybranej zmiennej indywidualnej (zmiennej blokowej) na zmienną zależną i ewentualnej interakcji zmiennej blokowej ze zmienną niezależną;

• minimalizować wariancję niekontrolowaną wywołaną zmienną blokową;

• Efektywność planu blokowego zależy od siły związku między zmienną blokową a zmienną zależną.

• Plan blokowy jest stosunkowo pracochłonny (dobór osób do bloków!). Alternatywą (jeśli nie ma interakcji zmiennej blokowej ze zmienną niezależną) jest zastosowanie analizy kowariancji z użyciem zmiennej indywidualnej jako zmiennej towarzyszącej (kowariantu).

5. Analiza kowariancji.

Oceniając wpływ zmiennej niezależnej (X) na zmienną zależną (Y) stwierdzamy, iż Y jest wysoko skorelowana z jakąś zmienną uboczną (C). Chcielibyśmy wyeliminować wpływ zmiennej ubocznej, gdyż utrudnia ona precyzyjne oszacowanie wpływu X na Y (zwiększa wariancję błędu).

Przykład fikcyjny (poglądowy).

Różne pociągi pokonują różne trasy (A₁, A₂, ... A_n) w różnym czasie (t₁, t₂ ..., t_n). Jest to spowodowane tym, że trasy mają różną długość oraz tym, że pociągi jeżdżą z różną szybkością. Ponieważ istnieje związek miedzy szybkością pociągu i czasem przejazdu danej trasy, możemy łatwo obliczyć w jakim czasie pociągi pokonywałyby różne trasy gdyby wszystkie jeździły z jednakową szybkością (czyli: gdyby wyeliminować wpływ szybkości pociągów)

Przykład psychologiczny.

Badamy wpływ metody nauczania (X) na poziom znajomości języka obcego uczniów (Y). Stwierdzamy jednak, że poziom zmiennej Y zależy od poziomu inteligencji badanych (C). Chcemy wyeliminować wpływ różnic indywidualnych w poziomie inteligencji aby bardziej precyzyjnie oszacować wpływ metody nauczania. Nie mamy możliwości takiego doboru uczniów, aby wszyscy mieli jednakową inteligencję (badamy jakąś rzeczywistą szkołę), możemy jednak wyeliminować wpływ inteligencji drogą analizy statystycznej.

Analiza kowariancji (analysis of covariance - ANCOVA) pozwala, drogą czysto STATYSTYCZNĄ, wyeliminować wpływ zmiennej ubocznej na zmienną zależną. Polega to (mówiąc w uproszczeniu) na przekształceniu wyników do takiej postaci, jak gdy wszyscy badani mieli identyczny poziom zmiennej ubocznej (np. identyczny poziom inteligencji w przykładzie powyżej). Eliminowana w taki sposób zmienna uboczna nazywa się: zmienną towarzyszącą, współzmienną lub kowariantem.

W szczególności, ANOCOVA pozwala:

• Oszacować wpływ zmiennej towarzyszącej na zmienną zależną.

• Oszacować wpływ zmiennej niezależnej na zmienną zależną z wyeliminowaniem wpływu zmiennej towarzyszącej (jak gdyby badani nie różnili się pod względem zmiennej towarzyszącej).

• Zmniejszyć wariancję niekontrolowaną a tym samym -- bardziej precyzyjnie oszacować wpływ zmiennej niezależnej na zmienną zależną.
  

• Skorygować średnie grupowe (tzw. adjusted means),
  tj. oszacować jakie byłyby średnie grupowe (poziom zmiennej zależnej) gdyby nie wpływała na nie zmienna towarzysząca (tzn. gdyby poziom zmiennej towarzyszącej był we wszystkich grupach jednakowy).

Efektywność ANCOVA-y zależy od siły związku (korelacji) między zmienną zależną i kowariantem. Jeśli korelacja ta jest bardzo niska, wynik analizy kowariancji nie będzie się wiele różnił od wyniku zwykłej analizy wariancji.

W ANCOVA wymagane jest aby:

• korelacja zmiennej zależnej i kowariantu (czyli: współczynnik regresji b dla kowariantu) była taka sama we wszystkich grupach (korygowanie wyników we wszystkich grupach można wówczas przeprowadzić
  w oparciu o identyczne równanie regresji);

• pomiar kowariantu był wolny od wpływu manipulacji eksperymentalnej. W wypadku badań eksperymentalnych oznacza to np., że kowariant powinien być mierzony przed podaniem instrukcji eksperymentalnej.

Analiza kowariancji: korygowanie danych surowych

Ogólne równanie regresji (dla jednego predyktora - X):

Y = a + bX

a - stała (constant, intercept ) równania regresji

b - współczynnik nachylenia linii regresji

Różnica między wynikiem otrzymanym Y_i a wynikiem oczekiwanym Y_i' dla osoby i :

Obliczanie średnich skorygowanych (adjusted mean)

gdzie:

- średnia skorygowana zmiennej Y w grupie i

- średnia nieskorygowana zmiennej Y w grupie i

- średnia zmiennej X dla grupy i

- średnia całkowita zmiennej X (dla całej próby)

b - współczynnikiem regresji dla kowariantu
(zmiennej towarzyszącej).

Zakładamy tu, że współczynnik b (nachylenie linii regresji) jest jednakowy we wszystkich grupach a zatem wszystkie wyniki możemy korygować w oparciu o ten sam współczynnik b.

ANOVA -- przykład liczbowy (SPSS)

Ob grupa z1 z2

01 1 3 4

02 1 4 5

03 1 5 6

04 1 7 7

05 2 5 4

06 2 6 5

07 2 8 8

08 2 9 9

anova z1 by grupa(1,2)/statistics=3.

* * * A N A L Y S I S O F V A R I A N C E * * *

* * * C E L L M E A N S * * *

TOTAL POPULATION: 5.88 (8)

GRUPA 1: 4.75 (4)

GRUPA 2: 7.00 (4)

Sum of Mean Signif

Source of Variation Squares DF Square F of F

Main Effects 10.125 1 10.125 3.240 .122

GRUPA 10.125 1 10.125 3.240 .122

Explained 10.125 1 10.125 3.240 .122

Residual 18.750 6 3.125

Total 28.875 7 4.125

ANCOVA - przykład liczbowy (SPSS)

compute c1 = z2.

manova z1 by grupa(1,2) with c1

/omeans /pmeans.

* * ANALYSIS OF VARIANCE -- DESIGN 1 * *

Source of Variation SS DF MS F Sign. of F

WITHIN CELLS 1.47 5 .29

REGRESSION 17.28 1 17.28 58.95 .001

CONSTANT .18 1 .18 .60 .473

GRUPA 3.41 1 3.41 11.63 .019

Regression analysis for WITHIN CELLS error term

Dependent variable .. Z1

COVARIATE B Beta Std. Err. t-Value Sig. of t

C1 .88636 .96011 .115 7.678 .001

Adjusted and Estimated Means Variable .. Z1

CELL Obs. Mean Adj. Mean Est. Mean Raw Resid. Std. Resid.

1 4.750 5.193 4.750 .000 .000

2 7.000 6.557 7.000 .000 .000

mtd5C (2008 / 2009) - 16

---