6. Metoda warunkowa

6.1. Model zagadnienia wyrównawczego

Metoda warunkowa polega na bezpośrednim wykorzystaniu związków pomiędzy wielkościami podlegającymi wyrównaniu. W trójkącie np. zachodzi

.

W metodzie warunkowej dla wielkości obserwowanych formułuje się układ „f” niezależnych równań warunkowych

W powyższym układzie równań, inaczej niż w metodzie parametrycznej, nie występują parametry - współrzędne punktów. Dzięki temu metoda warunkowa może być stosowana także w przypadku, gdy nie ma punktów stałych.

6.2. Przykłady równań warunkowych

h₁+ h₂ - h₃ + H_R2 - H_R1 = 0

h₂ - h₄ + h₅ = 0

h₃ - h₄ + h₆ = 0

α₁ + α₂ + α₃ - 200^g = 0

α₄ + α₅ + α₆ - 200^g = 0

α₇ - α₂ - α₃ = 0

α₁ + α₂ + α₃ - 3Ⴔ200^g +A_AB - A_CD = 0

d₁ cos(A_AB + α₁ - 200^g) - d₂ cos(A_AB + α₁ + α₁ - 400^g) - X_B + X_C = 0

d₁ sin(A_AB + α₁ - 200^g) - d₂ sin(A_AB + α₁ + α₁ - 400^g) - Y_B + Y_C = 0

Liczba równań warunkowych, defekt sieci. Liczbę równań warunkowych ustala się z wzoru

f = n - r + d

f - liczba równań warunkowych,

n - liczba obserwacji,

r - liczba niewiadomych,

d - defekt.

Defekt d może być zewnętrzny d_z i wewnętrzny d_w

d = d_z + d_w

Defekt zewnętrzny równa się liczbie stopni swobody całej sieci względem osi układu współrzędnych. Są to obroty i przesunięcia względem tych osi. Sieć jest swobodna jeśli defekt d_z Ⴙ 0.

Defekt wewnętrzny charakteryzuje możliwość wzajemnego przemieszczania się punktów sieci. Praktycznie jest to liczba brakujących obserwacji niezbędnych.

Defekt eliminuje nawiązanie sieci do punktów o znanych współrzędnych.

Przykłady sieci elementarnych

n = 3

d_z = 3

d_w = 1 (trójkąt może się powiększać)

d = d_z + d_w = 4

r = 3Ⴔ2 = 6

f = n - r + d= 3 - 6 + 4 = 1

n = 4

d_z = 1 (możliwy jest tylko obrót)

d_w = 0

d = d_z + d_w = 1

r = 2Ⴔ2 = 4

f = n - r + d = 4 - 4 + 1 = 1

n = 3

d_z = 1

d_w = 0

d = d_z + d_w = 0

r = 1Ⴔ3 = 2 (Rzędne H trzech punktów)

f = n - r + d = 3 - 2 + 0 = 1

n = 3

d_z = 1

d_w = 0

d = d_z + d_w = 0

r = 1 Ⴔ 3 = 2 (Rzędne H trzech punktów)

f = n - r + d = 3 - 2 + 0 = 1

n = 7

d_z = 3

d_w = 0

d = d_z + d_w = 3

r = 4 Ⴔ 2 = 8 (X,Y czterech punktów)

f = n - r + d = 7 - 8 + 3 = 2 .Dwa równa-nia wykorzystujące wzór sinusów.

6.3. Algorytm metody warunkowej

Jeśli w układzie

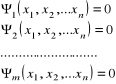
(6.1)

podstawić w miejsce x_i wyrażenie

x­­­_i = x_i^obs + v_i (6.2)

to uzyskujemy:

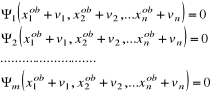
(6.3)

Co macierzowo zapisujemy w postaci

Jeśli równania (6.3) nie są liniowe, to każdą z funkcji ψ rozwijamy w szereg Taylora ograniczając się do pierwszych tj. liniowych wyrazów

. (6.4)

Szukamy następnie

gdzie
- minimalizuje funkcję celu
, a także spełnia równanie warunkowe

Bv + ၄ = 0 (6.5)

Przy rozwiązaniu r układu równań wprowadza się tzw. korelaty. Są to mnożniki

k = [k₁ , k₂ , ..... k_f]^T_,

których wektor wyznacza się ze wzoru

k = - (BP^-1B^T)^-1L (6.6)

Wektor poprawek i obserwacji wyrównanych wyznaczane są ze wzorów

v = P^-1B^Tk (6.7)

Wyrównane wartości rzędnych wyznaczane są na podstawie poprawek.

x^wyr = x^ob+ v (6.8)

w przypadku przewyższeń

h^wyr = h^ob + v

Kontrola 1 s = s'

v^TPv = - k^T L

Kontrola 2. Kontrola polega na sprawdzeniu warunków (6.1)

Ocena dokładności. Błąd średni wyrównanych wysokości wyznaczany jest jako funkcja wyrównanych wysokości

j = 1, 2....r (6.9)

gdzie

(6.10)

Błąd średni wyrównanych wysokości obliczany jest na podstawie macierzy wyrównanych obserwacji wyznaczanej ze wzoru

(6.11)

(6.12)

Wartości [C_x,wyr]_i,i odczytywane są z macierzy (6.11).

6.4. Przykład wyrównania sieci niwelacyjnej

Wyrównać sieć niwelacyjną metodą warunkową

Wyniki pomiaru

h₁^ob = - 0.663 m m­­₁ = 0,01 H_R1 = 111.770 m

h₂^ob = 2.308 m m₂ = 0,02 H_R2 = 115.430 m

h₃^ob = - 2.008 m m₃ = 0,02

h₄^ob = - 0.624 m m₄ = 0,01

h₅^ob = - 2.920 m m₅ = 0,02

h₆^ob = 1.370 m m₆ = 0,01

Obliczyć:

• wyrównane rzędne reperów H₁^wyr_­, H₂^wyr_, H₃^wyr,

• wyrównane wartości przewyższeń h₁^wyr, h₂^wyr, h₃^wyr, h₄^wyr h₅^wyr, h₆^wyr,

• ­­­błędy średnie wyrównanych wysokości m_H1, m_H2, m_H3,

• błędy średnie wyrównanych przewyższeń m_hi.

Liczba równań warunkowych

n = 6, r = 3, d = d_z + d_w = 0

f = n - r + d = 6 - 3 + 0 = 3

Równania warunkowe

h₂ - h₄ + h₅= 0

h_{1 +} h₂ - h₃ + H_R1 - H_R2 = 0

- h₃ + h₄ - h₆ = 0

Po podstawieniu h_i = h_i^ob + v_i

h₂^ob + v₂ - h₄^ob - v₄ + h₅^ob + v₅ = 0

h₁^ob + v₁ + h₂^ob + v₂ - h₃^ob - v₃ + H_R1 - H_R2 = 0

-h₃^ob - v₃ + h₄^ob + v₄ - h₆^ob - v₆ = 0

Układ równań warunkowych

v₂ - v₄ + v₅ + 0.012 = 0

v₁ + v₂ - v₃ - 0.007 = 0

- v₃ + v₄ - v₆ + 0.014 = 0

Zestawienie macierzy

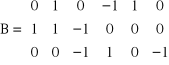
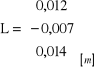
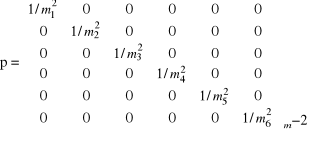
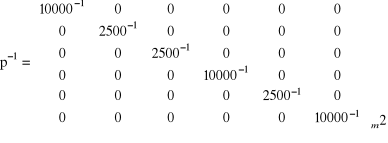
Wektor korelat k = - (BP^-1B^T)^-1L

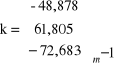
Wektor poprawek v = P^-1B^Tk

i wektor obserwacji (przewyższeń) wyrównanych h^wyr = h^ob + v

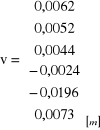
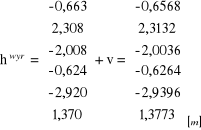
Wyrównane wysokości reperów H^wyr = F_j (h^wyr)

H₁^wyr = H_Rp1 + h₁^wyr = 111.1132

H₂^wyr = H_Rp2 + h₃^wyr = 113.4264

H₃^wyr = H_Rp2 - h₆^wyr = 114.0527

Kontrola 1. s = s'

s = v^TPv = 2.036732

s' = - k^T L = 2.036732

Kontrola 2. Sprawdzenie warunków

h₂ - h₄ + h₅ = 0,0000

h_{1 +} h₂ - h₃ + H_R1 - H_R2 = 0,0000

- h₃ + h₄ - h₆ = 0,0000

Ocena dokładności

Błąd wyrównanych wysokości

Dla wyznaczenia wysokości H₁, H₂, H₃ przyjęto następujące zależności:

H₁ = H_Rp1 + h₁

H₂ = H_Rp2 + h₃

H₃ = H_Rp2 - h₆

Wzory te wykorzystano przy wyznaczaniu błędów średnich wyrównanych wartości rzędnych H₁, H₂, H₃ 

Błąd średni wyrównanej wysokości H₁

0,0001
2,5854E-05

= 5,03387-05

m_H1 = 0,0071 [m]

Błąd średni wyrównanej wysokości H₂

0,0004
- 1,1994E-08

= 0,00027157

m_H2 = 0,0165 [m]

Błąd średni wyrównanej wysokości H₃

= 4,63646E-05

m_H3 = 0,0068 [m]

Błędy średnie wyrównanych obserwacji h_i^wyr

m_h1 = 0,0071 [m]

m_h2 = 0,0093 [m]

m_h3 = 0,0084 [m]

m_h4 = 0,0071 [m]

m_h5 = 0,0084 [m]

m_h6 = 0,0068 [m]

45

Rp. 1

Rp. 2

H.1

H.2

H.3

h ₁

h ₂

h ₃

h ₄

h ₅

α₁

α₂

α₃

α₄

α₆

α₅

α₇

A °

°

B

°

C

d₁

D

°

α₁

d₂

α₂

α₃

α₁

α₂

α₃

α₁

α₂

α₃

l

A

h ₆

h ₅

h ₄

h ₃

h ₂

h ₂

h ₃

h ₁

h ₂

h ₃

h ₁

Rp

α₁

α₂

l

l

l

α₃

α₄

h ₆

h ₁

H.3

H.2

H.1

Rp. 2

Rp. 1

---