WŁASNOŚCI FUNKCJI - poziom podstawowy
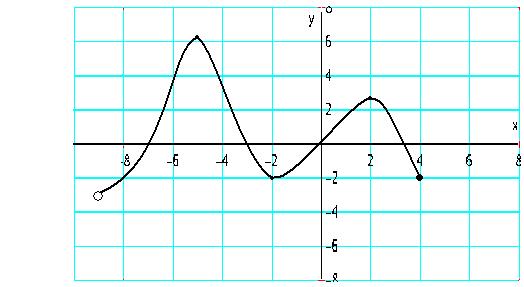
Zad. 1 (3p) Na rysunku przedstawiony jest wykres funkcji ![]()
.
podaj dziedzinę i zbiór wartości funkcji
Podaj przedziały, w których funkcja jest malejąca.
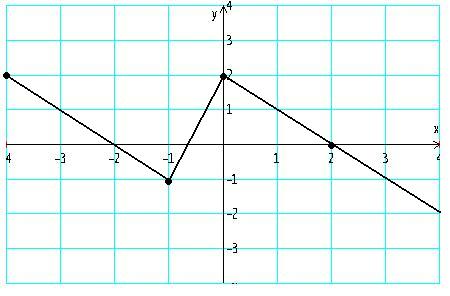
Zad. 2 (3p) Dana jest funkcja ![]()
. Naszkicuj wykres funkcji ![]()
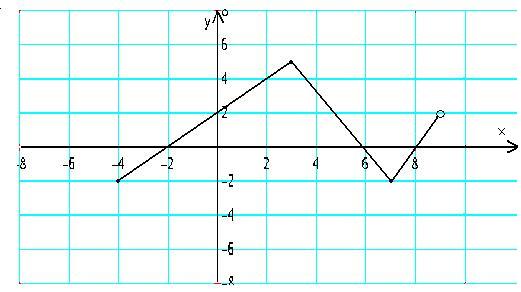
Zad. 3 (4p) Na rysunku przedstawiono wykres funkcji ![]()
. Podaj wszystkie rozwiązania równania ![]()
należące do przedziału ![]()
.
Zad. 4 (5p) Funkcja ![]()
została określona za pomocą tabelki:
|
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
5 |
2 |
1 |
2 |
3 |
-3 |
-5 |
wyznacz dziedzinę i zbiór wartości funkcji
naszkicuj wykres funkcji f
uzasadnij, że funkcja f nie jest różnowartościowa
Zad. 5 (3p) Na rysunku przedstawiono wykres funkcji f :![]()
Na podstawie wykresu:
określ zbiór wartości funkcji f
wyznacz zbiór argumentów dla których funkcja przyjmuje wartości dodatnie
wyznacz te argumenty, dla których funkcja przyjmuje wartość równą 4.
Zad. 6 (3p) Naszkicuj wykresy funkcji danych wzorami ![]()
, ![]()
, ![]()
Zad. 7 (3p) Dana jest funkcja f określona następująco ![]()
naszkicuj wykres funkcji dla
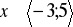
na podstawie narysowanego wykresu określ dla jakich x funkcja przyjmuje wartości dodatnie.
Zad. 8 (4p) Dana jest funkcja f określona wzorem 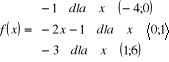
narysuj wykres funkcji f
podaj dziedzinę i zbiór wartości funkcji f .
Zad. 9 (3p) Wyznacz dziedzinę funkcji ![]()
. Podaj jej wartość największą.
Zad. 10 (4p) Dana jest funkcja ![]()
oblicz
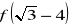
i przedstaw tę wartość w postaci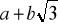
, gdzie a i b są liczbami wymiernymioblicz x, jeśli
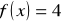
.
Zad. 11 (4p) Uzupełnij tabelkę funkcji f, wiedząc, że funkcja f jest liniowa
x |
-4 |
|
-1 |
2 |
3 |
|
|
f(x) |
|
-3 |
5 |
-4 |
|
-10 |
|
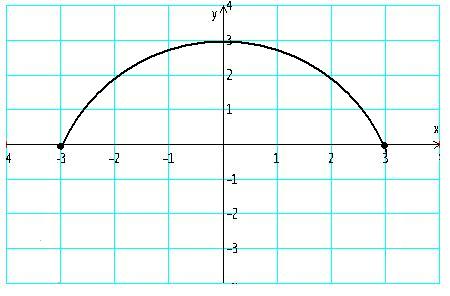
Zad. 12 (3p) Rysunek przedstawia wykres funkcji f
narysuj wykres funkcji
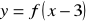
narysuj wykres funkcji
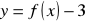
podaj zbiór wartości funkcji
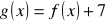
Zad. 13 (5p) Pani Anna zatrudniła się w butiku na 20 dni roboczych. Będzie zarabiała 40 zł dziennie plus 5 zł za każdą sprzedaną sztukę odzieży.
podaj wzór określający funkcję f wartości dochodu pani Anny
podaj dziedzinę funkcji f
oblicz ile zarobiłaby, gdyby sprzedała 10 sztuk odzieży
oblicz, ile sztuk odzieży sprzedała jeśli zarobiła więcej niż 1100 zł.
Zad. 14 (5p) Dana jest funkcja f określona wzorem ![]()
sprowadź wzór do najprostszej postaci
oblicz
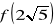
wyznacz maksymalny przedział w którym wartości tej funkcji są ujemne.
Zad. 15 (3p) Wyznacz dziedzinę funkcji ![]()
Zad. 16 (4p) Wyznacz miejsca zerowe funkcji 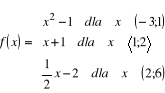
Zad. 17 (2p) Wyznacz wartości liczby m, tak aby funkcja![]()
miała miejsce zerowe x= -1.
Zad. 18 (3p) Dana jest funkcja f określona wzorem ![]()
, ![]()
zapisz wzór tej funkcji bez użycia symbolu wartości bezwzględnej
narysuj wykres tej funkcji
podaj zbiór wartości funkcji f .
Zad. 19 (3p) Cena biletu na autobus lokalny jest funkcją liczby przejechanych pełnych kilometrów. Napisz wzór tej funkcji, jeśli wiadomo że opłata stała to złotówka, a za każdy przejechany kilometr dolicza się 20 groszy. Przyjmujemy, że odległość między kolejnymi przystankami to 2 km.
oblicz na którym przystanku wysiadł pasażer, który wsiadł na przystanku początkowym i zapłacił 1,80 zł
wyznacz cenę maksymalną biletu na autobus, który zatrzymuje się na 24 przystankach
Zad. 20 (5p) Dana jest funkcja 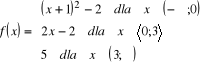
wyznacz f(1) oraz f(100)
wyznacz x jeśli wiadomo, że f(x)=7.
Zad. 21 (3p) Funkcja f przyporządkowuje każdej liczbie naturalnej n należącej do przedziału ![]()
liczbę jej naturalnych dzielników różnych od 1 i od n
sporządź tabelkę wartości tej funkcji
podaj zbiór wartości funkcji
podaj zbiór wartości funkcji f, jeśli dziedziną byłby zbiór liczb pierwszych.
Zad. 22 (5p) Wyznacz wartość liczby m, tak aby funkcja ![]()
była rosnąca
aby do wykresu funkcji należał punkt
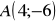
.
Zad. 23 (3p) Dana jest funkcja f określona wzorem 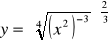
przedstaw wzór w postaci
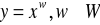
uzasadnij, że funkcja nie ma miejsc zerowych.
Zad. 24 (5p) Dana jest funkcja ![]()
wyznacz wszystkie wartości m, tak aby funkcja f osiągała wartość największą
wyznacz wszystkie liczby m, tak aby funkcja f była stała.
Zad. 25 (2p) Zapisz w jak najprostszej postaci wyrażenie 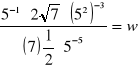
.
Czy funkcja o współczynniku kierunkowym w jest malejąca?
Zad. 26 (2p) W pewnym doświadczeniu badano w jaki sposób ciśnienie P gazu wypełniającego balon zmienia się w zależności od objętości V.
Wyniki przedstawia tabela:
V |
2 |
2,5 |
3 |
3,5 |
4 |
5 |
P |
30 |
24 |
20 |
20 |
15 |
12 |
Zaznacz te wyniki w układzie współrzędnych. Wiedząc, że jeden z wyników jest błędny, podaj wzór zależności objętości od ciśnienia.
Zad. 27 (4p) Funkcja przyporządkowuje każdej liczbie rzeczywistej x є{-4,-3,-2,-1,0,1,2,3,4,5,6} jej wartość bezwzględną pomniejszoną o 2.
a) Naszkicuj wykres tej funkcji b) podaj jej miejsce zerowe c) wyznacz zbiór wartości
Zad. 28 (2p) Funkcja f określona jest grafem
Podaj jej zbiór wartości i miejsca zerowe.
Zad. 29 (4p) Funkcja przyporządkowuje każdej liczbie rzeczywistej x є {2,3,4,5,6,7,8} jej największy dzielnik różny od niej samej.
a) Naszkicuj wykres tej funkcji , b) Wyznacz jej zbiór wartości.
Zad. 30 (2p) Funkcja f każdej dodatniej liczbie całkowitej przyporządkowuje jej resztę z dzielenia przez 7.
a) Wyznacz zbiór wartości funkcji f
b) Narysuj wykres funkcji f dla argumentów mniejszych od 16 .
Zad. 31 (2p) Dziedziną funkcji f jest przedział <-3;6> , a jej zbiorem wartości przedział <-4;1>. Funkcja ma dwa miejsca zerowe. Naszkicuj przykład wykresu funkcji f i zapisz dla jakich argumentów Twoja funkcja przyjmuje wartości dodatnie.
Zad. 32 (3p ) Narysuj wykres funkcji f(x) = 2x , a następnie korzystając z jej wykresu wykres funkcji g(x) =![]()
*2x.
Zad. 33 (3p) Funkcja f każdej liczbie całkowitej zbioru {0,1,2,3…10} przyporządkowuje jej resztę z dzielenia przez 4.
a) Wyznacz zbiór wartości funkcji f
b) Narysuj jej wykres
c) Wyznacz jej miejsce zerowe.
Zad. 34 (3p) Na rysunku przedstawiono wykres funkcji f .Narysuj wykresy
funkcji:
y = f(x) + 2 b) y = f(x - 3) c) y = f(x + 2) - 4
Zad.35 (5p) Dany jest trójkąt równoramienny o ramieniu długości
24. Wyznacz wzór funkcji, która podstawie trójkąta przyporządkowuje
jego obwód. Podaj dziedzinę i zbiór wartości tej funkcji.
Zad. 36 (4p) Funkcje f przyporządkowuje liczbom n mniejszym od 10 liczbę dwuelementowych kombinacji zbioru n - elementowego. Podaj wzór , dziedzinę i zbiór wartości oraz określ monotoniczność funkcji.
Zad. 37 (5p) Sprawdź , czy funkcje f i g mają takie same miejsca zerowe , jeśli f(x) =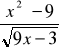
, g(x) = |x| - 3
Zad. 38 (3p) Naszkicuj wykres funkcji f(x) = ![]()
dla x є <0;9> oraz wykresy funkcji h(x) = f(x + 3) i g(x) = f(x) + 5.
Zad. 39 (4p) Dana jest funkcja f(x) = x3 + ax - 1. Wyznacz parametr a, jeśli wiadomo , że do wykresu tej funkcji należy punkt A(-2;3). Dla jakich argumentów wartości tej funkcji są większe od wartości funkcji g(x) = x3 + 2x2 -1 ?
Zad. 40 (6p) Dana jest funkcja f(x) = (9-m2)x + m - 1. Wyznacz parametr m tak aby:
a) do wykresu należał punkt A(1,6) b) funkcja była rosnąca c) wykres funkcji był równoległy do wykresu funkcji y = 3x - 7.
Zad. 41 (5p) Dla jakich wartości parametru m funkcja f(x) = (|2m-1|-2)x2- (m-1)x +10 ma wartość największą. Dla jakich wartości m funkcja ta jest liniowa?
Zad. 42 (6p) Liczbom naturalnym n![]()
{2,3,4,5,6,7,8,9,10} przyporządkowujemy liczbę NWD(n,12). Naszkicuj wykres tej funkcji. Oblicz , o ile największa wartość tej funkcji jest większa od największej wartości funkcji f(x) = -x2 + 4.
Zad. 43 (4p) Dana jest funkcja f(x) = (m2-m)x +5 . Wyznacz parametr m, aby
a) funkcja nie miała miejsc zerowych b) miejscem zerowym była liczba -4.
Zad 44 (7p) Wyznacz dziedzinę funkcji f(x) = ![]()
+![]()
. Naszkicuj wykresy funkcji y = f(x) , y = f(x)+2 , y = f(x - 4).
Zad. 45 (7p) dana jest funkcja f(x) = 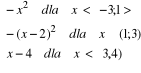
![]()
Naszkicuj jej wykres , podaj miejsca zerowe oraz przedziały , w których funkcja jest malejąca.
Zad. 46 (5p) Jaką wartość powinien przyjąć parametr m, aby funkcja f(x) = 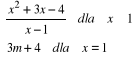
była funkcją liniową?
Zad. 47 (4p) Funkcja f przyporządkowuje każdej liczbie naturalnej dodatniej n cyfrę , która znajduje się na n - tym miejscu rozwinięcia dziesiętnego ułamka 4/11 . Wykaż, że zbiór wartości tej funkcji jest dwuelementowy. Oblicz f(930) i f (315).
Zad. 48 (5p) Liczbom naturalnym n є{2,3,4,5,9,10} przyporządkowujemy taką najmniejszą liczbę x , że po dopisaniu x na końcu liczby 533 otrzymamy czterocyfrową liczbę podzielną przez n. Naszkicuj wykres tej funkcji i podaj miejsca zerowe.
Zad. 49 (6p) Liczbom naturalnym z przedziału (-3;8> przyporządkujemy mniejszą spośród liczb {n,4} , a jeśli n = 4 to liczbę 4. Naszkicuj wykres tej funkcji oraz wykres funkcji f (x + 6).
Zad. 50 (5p) Napełnianie basenu odbywa się za pomocą sześciu jednakowo wydajnych zaworów. Jeżeli otwarte są trzy z nich to basen napełnia się w ciągu 24 godzin.
Podaj wzór funkcji f, która opisuje zależność pomiędzy liczbą otwartych zaworów, a liczbą godzin , w ciągu których basen się napełni.
Podaj dziedzinę i zbiór wartości funkcji f
Dobierz odpowiednia jednostkę na osi odciętych i naszkicuj wykres funkcji f
Uzasadnij , że funkcja jest malejąca
Zad. 51 (5p) Funkcja f(x) jest określona wzorem f(x) =![]()
![]()
Sprawdź czy liczba a = (0,25) -0,5 należy do dziedziny funkcji f
Oblicz f(2) i f(3)
Sporządź wykres funkcji f(x)
Podaj rozwiązanie równania f(x) = 0
Wyznacz zbiór wartości funkcji f(x).
Zad. 52 (4p) Dana jest funkcja NWD(x,4) da x![]()
{1,2,3,4,5,6,7,8}
Uzupełnij tabelkę
Naszkicuj wykres
Podaj zbiór wartości funkcji y = f(x) + 3.
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
f(x) |
|
|
|
|
|
|
|
|
Odpowiedzi
WŁASNOŚCI FUNKCJI - poziom podstawowy
1. a) ![]()
![]()
b) ![]()
![]()
3. ![]()
1
3
6
9
0
8
1
5
2
Wyszukiwarka
Podobne podstrony:
4 Ogolne wlasnoci funkcji, Zarządzanie studia licencjackie, matematyka
Matematyka II (Ćw) - Lista 01. Wykresy i własności funkcji, odpowiedzi do zadania 2
wlasnosci funkcji, Matematyka, Liceum
Matematyka Własności funkcji
wlasnosci funkcji, Matematyka, Liceum
Własności funkcji jednej zmiennej, Analiza matematyczna
Podstawowe wlasnosci funkcji zadania domowe
Wzór funkcji y, SZKOŁA, Matematyka, Matematyka
WŁASNOŚCI FUNKCJI ODCZYTYWANE Z WYKRESU
Ochrona wlasnosci intelektualnej wyklad 1, Matematyka studia, Ochrona Własności Intelektualnej
Funkcja kwadratowa, matematyka
Funkcja liniowa, Matematyka
zagadnienia, punkt 6, VI Własności funkcji ciągłych na zbiorach zwartych (tw
Funkcje i ich własności Funkcje i ich własności 2, zadania
Własność funkcji
10 Wlasnosci funkcji ciaglych Nieznany (2)
więcej podobnych podstron