„Nie ma sensu w byciu

precyzyjnym, jeśli nie wiesz

nawet, o czym mówisz.”

John von Neumann

WŁASNOŚCI FUNKCJI.

Miejsce zerowe, monotoniczność, wartość
najmniejsza i największa to najprostsze
własności

funkcji

które

poznajesz

w

gimnazjum. Zdobądź porządne podstawy a
nie będziesz miał problemów z funkcjami w
szkole ponad gimnazjalnej.

DEFINICJA FUNKCJI.

Funkcją określoną na zbiorze X o

wartościach w zborze Y nazywamy takie

przyporządkowanie, które każdemu

elementowi x należącemu do zbioru X

przyporządkowuje dokładnie jeden

element y ze zboru Y.

UWAGA

Podkreślone elementy definicji są bardzo
ważne. Niespełnienie któregoś z nich
sprawia, że dane przyporządkowanie nie jest
funkcją.

Dla przypomnienia:

MIEJSCE ZEROWE

FUNKCJI.

Miejsce zerowe funkcji jest to ten

argument x  X, dla którego wartość

funkcji jest równa zero (f(x) = 0).

UWAGA

Zgodnie z definicją miejsce zerowe to argument

funkcji a nie punkt. Często popełnianym błędem jest

podawanie miejsca zerowego jako punktu postaci

(x, 0). Miejsce zerowe to argument, nie punkt.

Funkcja może mieć wiele miejsc zerowych, może

również nie mieć miejsc zerowych.

PRZYKŁADY.

PRZYKŁAD 1.
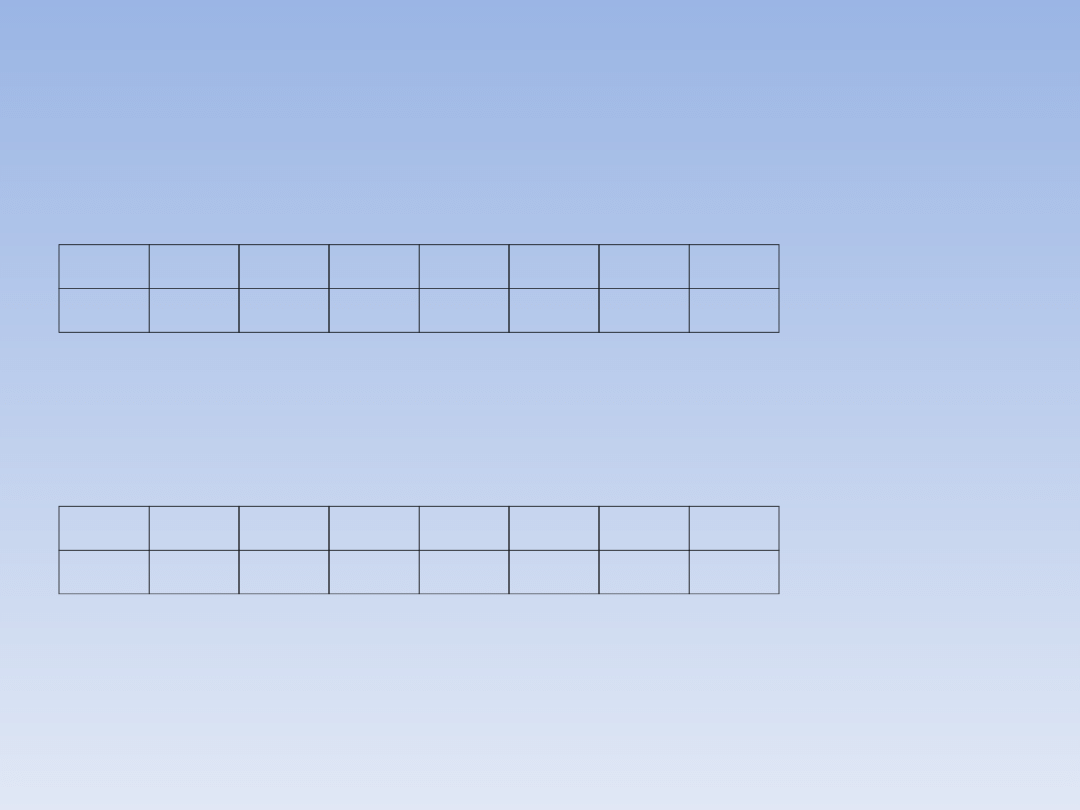
Funkcja f określona jest tabelą:

Jakie są jej miejsca zerowe?

Musimy znaleźć te x dla których y = 0

Miejsca zerowe tej funkcji to x = 3 oraz x = 11

x

-1

0

3

5

9

11

13

y

-12

4

0

8

-1

0

14

x

-1

0

3

5

9

11

13

y

-12

4

0

8

-1

0

14

PRZYKŁADY.

PRZYKŁAD 2.
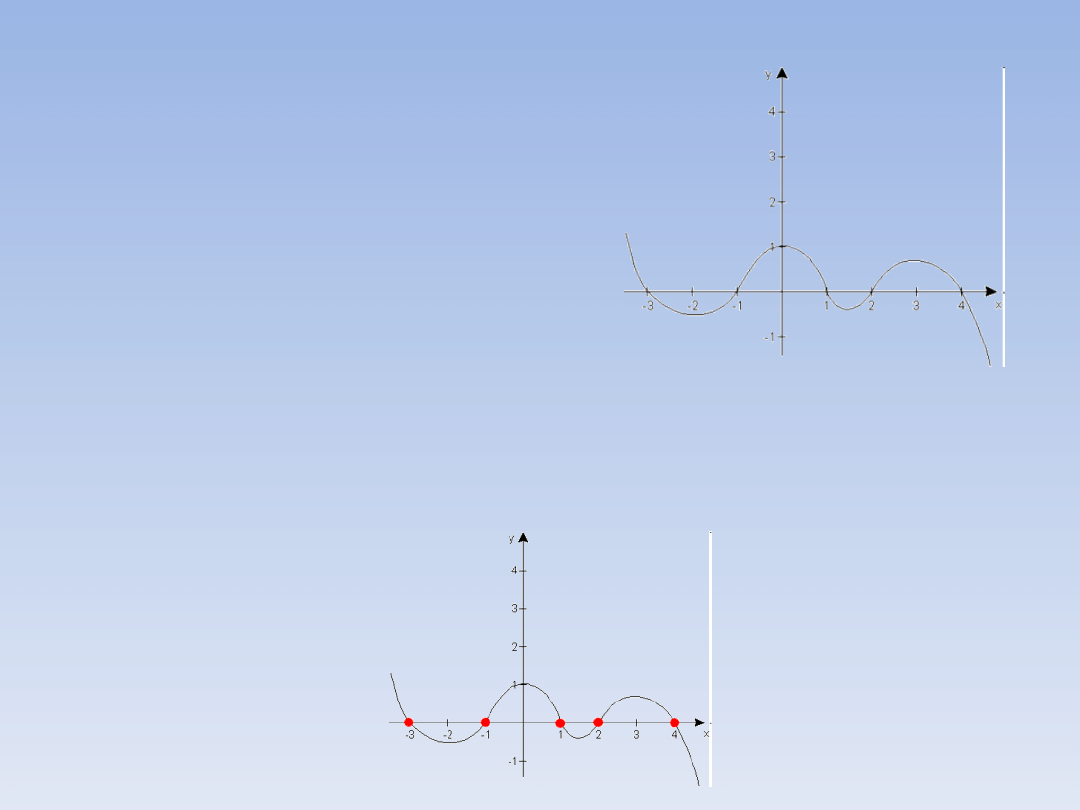
Funkcję f przedstawiono na
wykresie obok. Jakie są miejsca
zerowe tej funkcji?

Na wykresie bardzo łatwo odczytać miejsca
zerowe funkcji. Wystarczy odczytać x w
których wykres przecina oś OX. Miejsca
zerowe tej funkcji to: x = -3, x = -1, x = 1, x
= 2 i x = 4

PRZYKŁADY.

PRZYKŁAD 3.
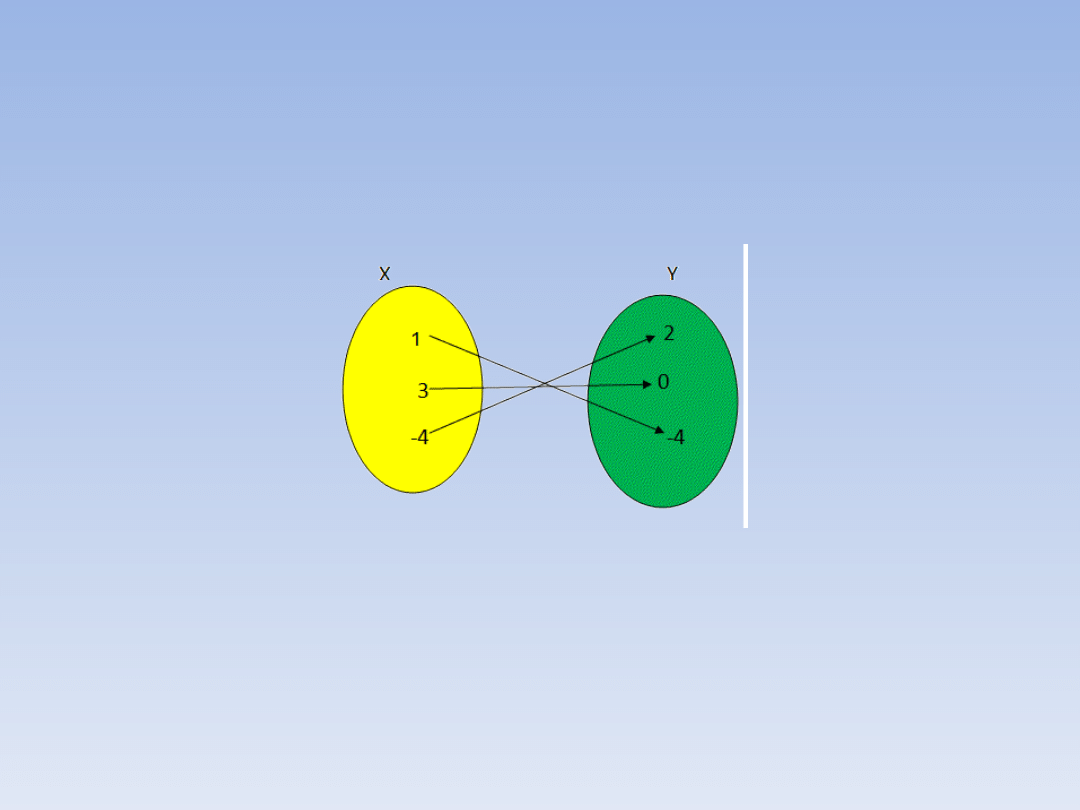
Funkcję f określono grafem. Znajdź jej
miejsca zerowe.

Miejscem zerowym jest ten x, któremu
przyporządkowano 0, a więc miejscem
zerowym funkcji określonej powyższym
grafem jest x = 3

PRZYKŁADY.

PRZYKŁAD 4.
Znajdź miejsce zerowe funkcji określonej
wzorem
y = 2x – 4.
Ab znaleźć miejsce zerowe funkcji określonej
wzorem korzystamy bezpośrednio z definicji:
miejsce zerowe funkcji to ten x dla którego y
=

0.

Wstawiamy

do

wzoru

y = 0 i rozwiązujemy równanie:
0 = 2x – 4
4 = 2x /:2
2 = x
Miejscem zerowym tej funkcji jest x = 2.

MONOTONICZNOŚĆ

FUNKCJI.

Monotoniczność funkcji to określenie, czy
funkcja rośnie, jest stała czy maleje.

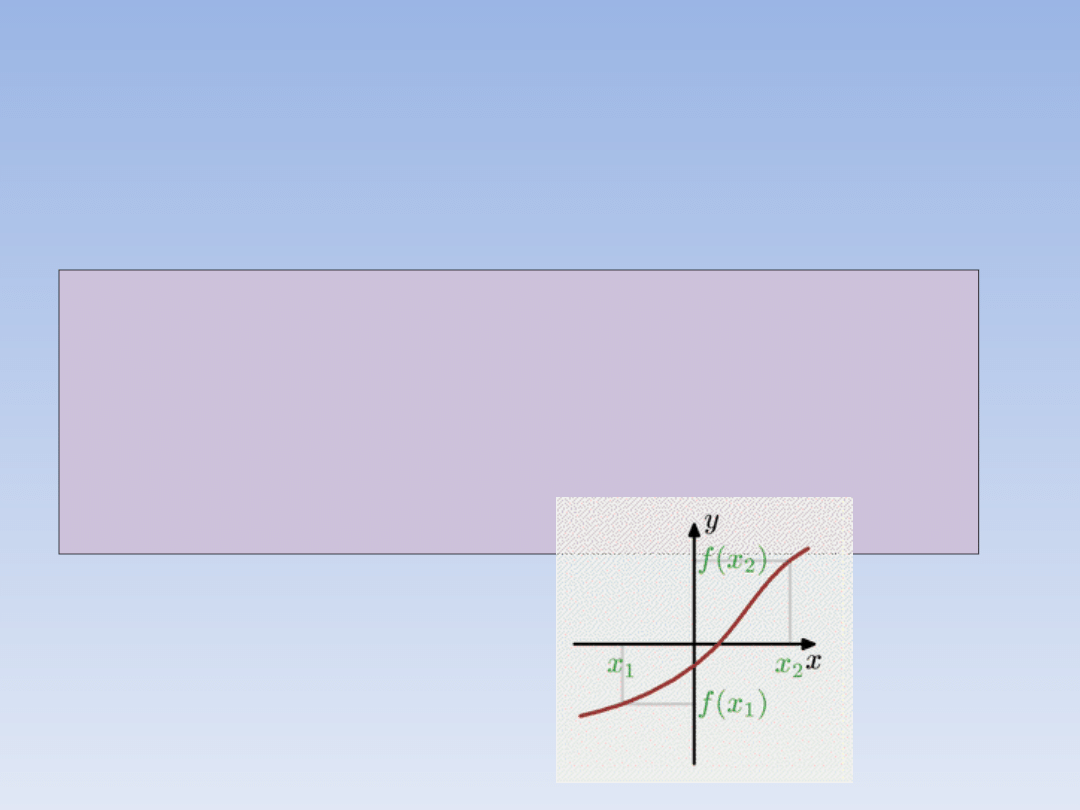
Wykres funkcji rosnącej:

Funkcja f jest rosnąca gdy dla coraz

większych argumentów wartości funkcji są

coraz większe, czyi gdy dla każdego x

1

 X

i x

2

 X takich, że x

1

< x

2

zachodzi: f(x

1

) <

f(x

2

)

MONOTONICZNOŚĆ

FUNKCJI.

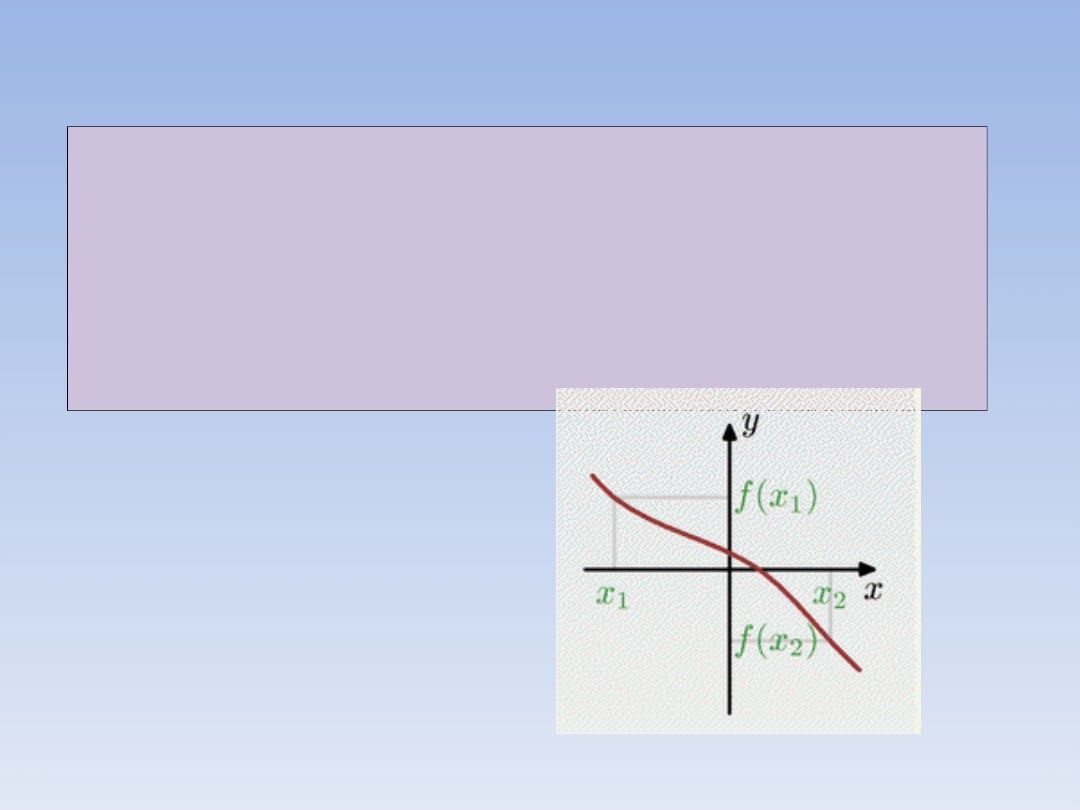
Funkcja f jest malejąca gdy dla coraz

większych argumentów wartości funkcji są

coraz mniejsze, czyi gdy dla każdego x

1



X i x

2

 X takich, że x

1

< x

2

zachodzi: f(x

1

)

> f(x

2

)

Wykres funkcji malejącej:

MONOTONICZNOŚĆ

FUNKCJI.

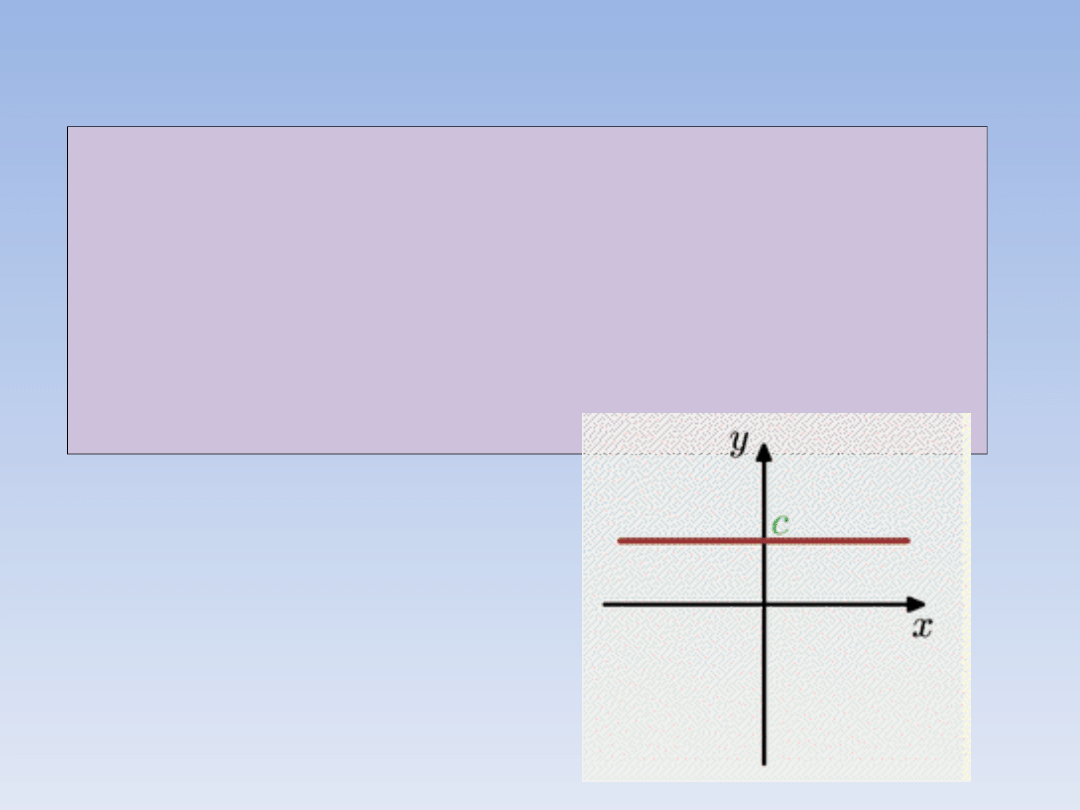
Funkcja f jest stała gdy po mimo zmiany

argumentów wartości funkcji się nie

zmieniają, czyi gdy dla każdego x

1

 X i x

2

 X zachodzi: f(x

1

) = f(x

2

).

Wzór takiej funkcji to f(x) = c gdzie c to

stała (liczba, np. f(x) = 3)

Wykres funkcji stałej:

NAJMNIEJSZA I NAJWIĘKSZA

WARTOŚĆ FUNKCJI.

Tych pojęć chyba nie trzeba definiować. Po
prostu najmniejsza wartość funkcji to
najmniejszy y jaki przyjmuje funkcja, a
największa wartość funkcji to największy y
jaki przyjmuje funkcja.

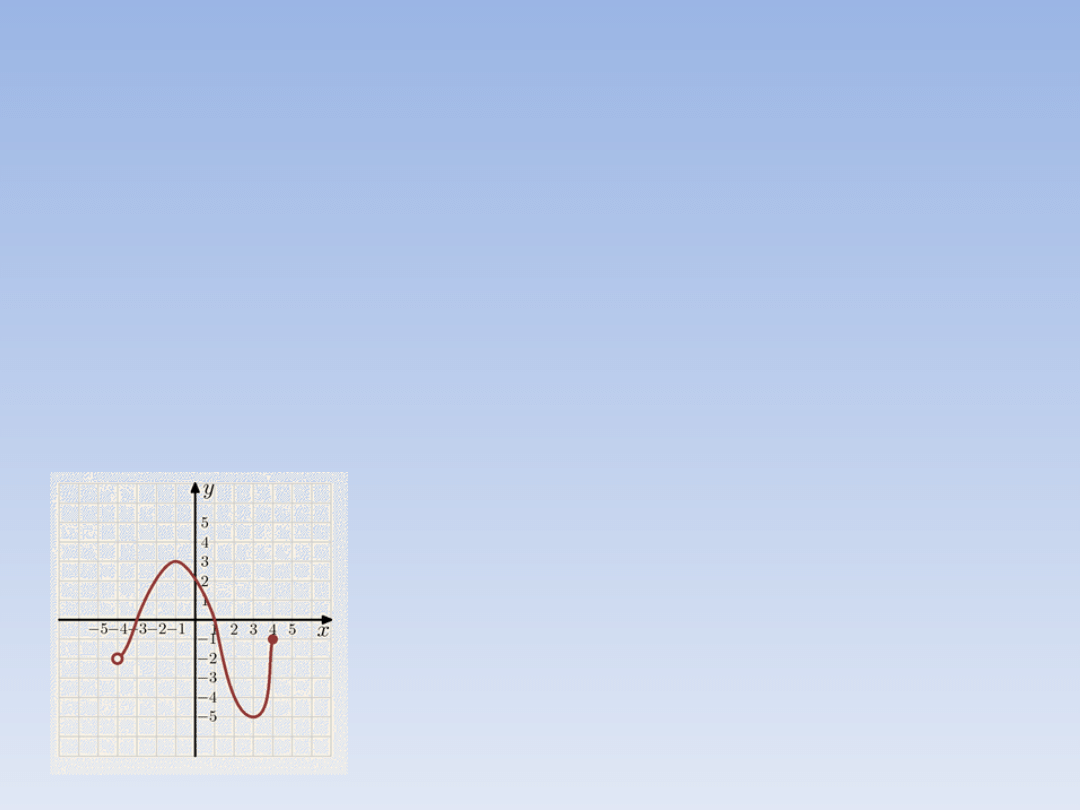
PRZYKŁAD 1.

Wartość największa tej funkcji:
y

max

= 3

Wartość najmniejsza tej funkcji
y

min

= -5

PRZYKŁADY.

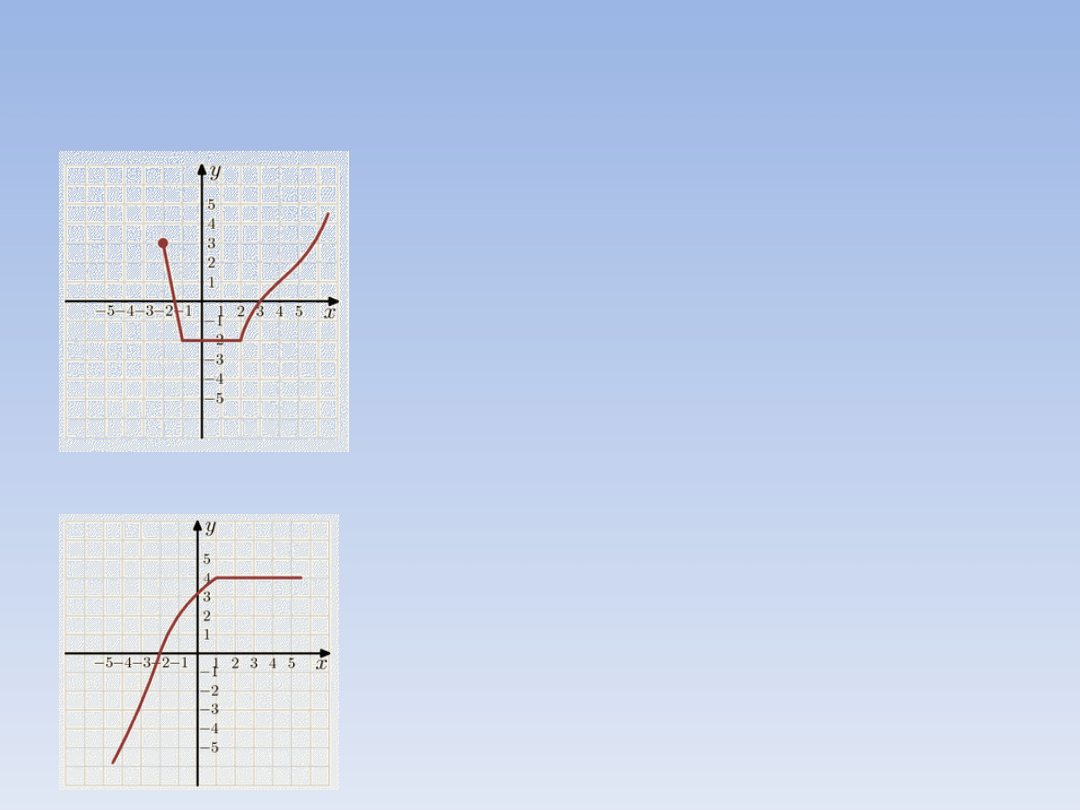
PRZYKŁAD 2.

Funkcja ta nie ma wartości największej
(wykres biegnie w górę i po prawej nie
kończy się „kółeczkiem” więc rośnie w
nieskończoność).
Wartość najmniejsza: y

min

= -2.

PRZYKŁAD 3.
Wartość największa: y

max

= 4.

Funkcja ta nie ma wartości najmniejszej
(wykres biegnie w dół i nie kończy się
„kółeczkiem”

więc

funkcja

maleje

w

nieskończoność)

PRZYKŁADY.

PRZYKŁAD 4.
Podaj wartość największą i najmniejszą
określonej tabelą funkcji.

Wystarczy podać najmniejszy i największy y
z tabeli.

y

max

= 4

y

min

= -4

x

0

1

2

3

4

y

-1

3

4

-4

3

x

0

1

2

3

4

y

-1

3

4

-4

3

WARTOŚCI DODATNIE I

UJEMNE NA WYKRESIE

FUNKCJI.

Z wykresu funkcji łatwo odczytać gdzie
funkcja przyjmuje wartości dodatnie a gdzie
ujemne.

Jeśli wykres biegnie nad osią OX funkcja
przyjmuje wartości dodatnie.

Jeśli wykres biegnie pod osią OX funkcja
przyjmuje wartości ujemne.

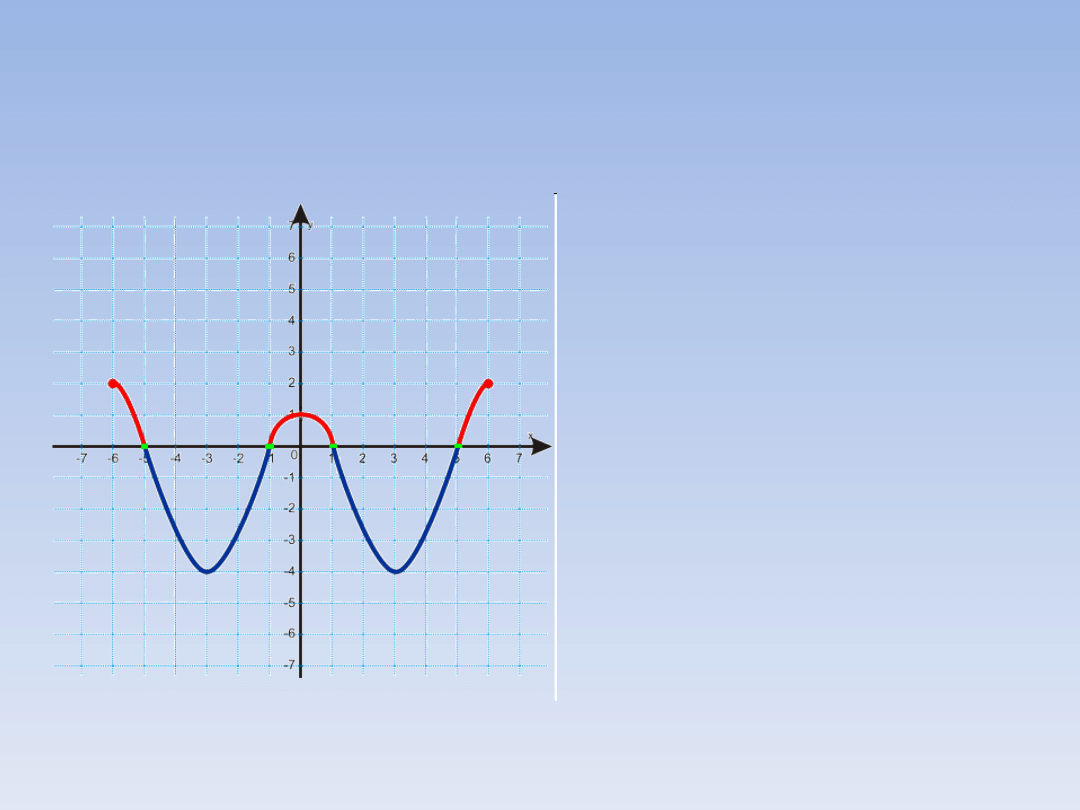
WARTOŚCI DODATNIE I

UJEMNE NA WYKRESIE

FUNKCJI.

Na wykresie
kolorem
czerwonym
zaznaczono
miejsca, w których
funkcja przyjmuje
wartości dodatnie,
na zielono miejsca
zerowe, a na
niebiesko miejsca
w których funkcja
przyjmuje wartości
ujemne.

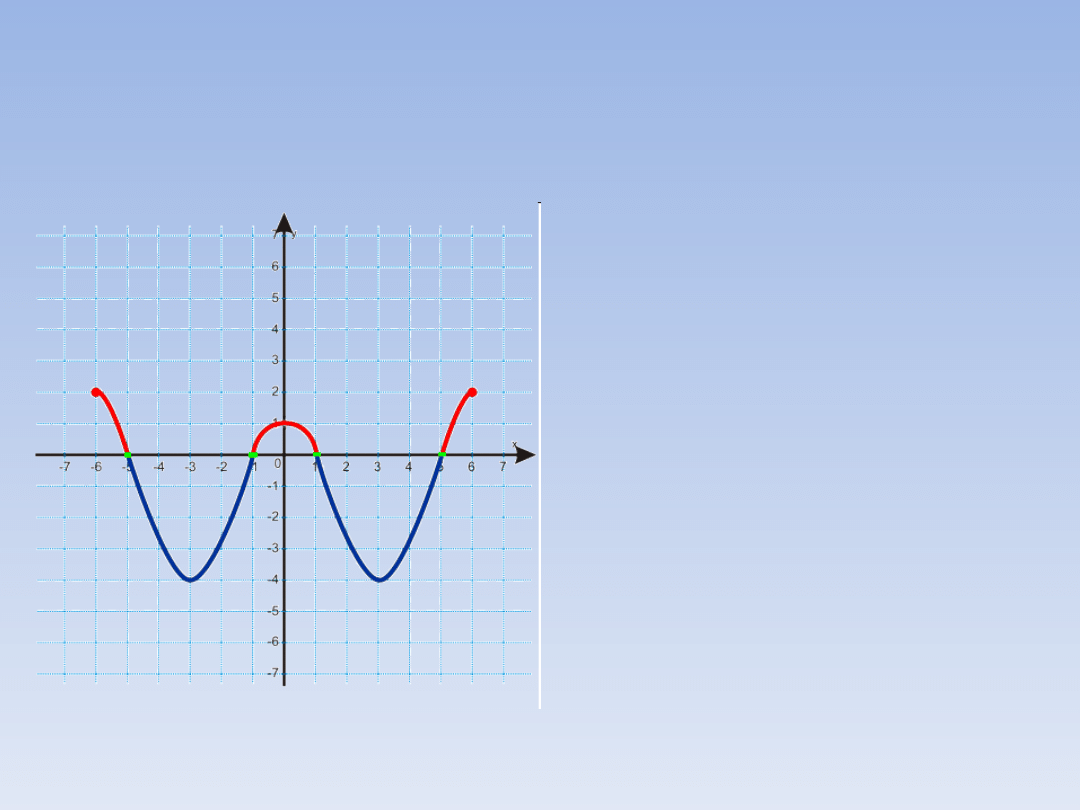
WARTOŚCI DODATNIE I UJEMNE

NA WYKRESIE FUNKCJI.

Z wykresu można
odczytać, że funkcja
przyjmuje wartości
dodatnie dla
x  [-6, -5), dla x  (-

1, 1) i dla x  (5, 6].

Wartości ujemne
funkcja przyjmuje dla
x  (-5, -1) i dla x 

(1, 5).
Miejsca zerowe tej
funkcji to x = -5, x =
-1, x = 1 i x = 5.

PRZYKŁADOWE ZADANIA.

Zadanie 1.
Odczytaj z wykresu własności funkcji:
- dziedzinę,
-zbiór wartości,
- miejsca zerowe funkcji,
- monotoniczność,
- w jakich przedziałach funkcja przyjmuje
wartości ,dodatnie a w jakich ujemne,
- wartość największą i najmniejszą.

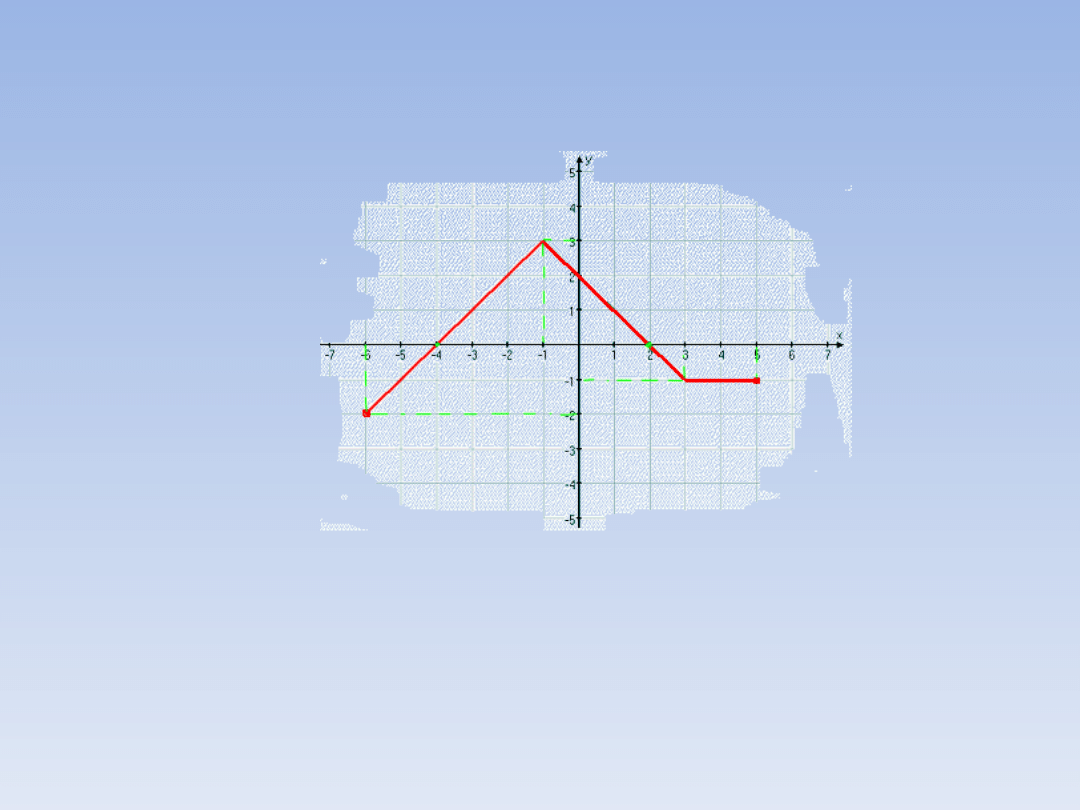
PRZYKŁADOWE ZADANIA.

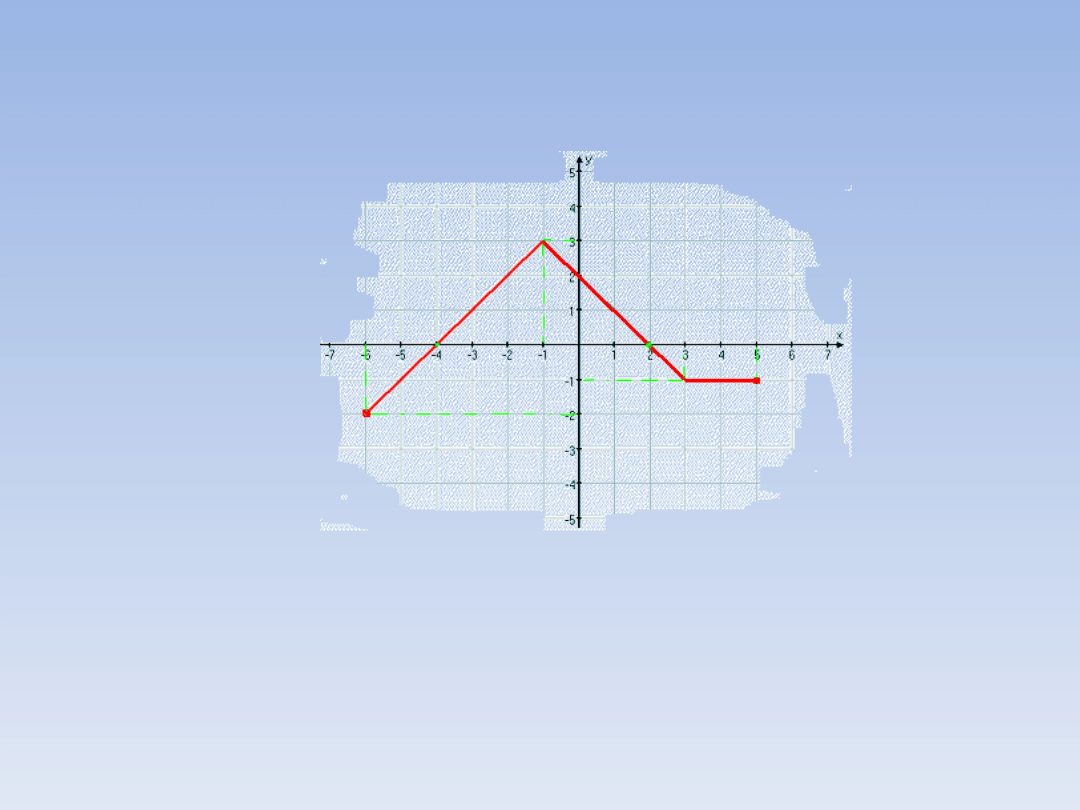
Zadanie 1 – ciąg dalszy.

- Dziedzinę funkcji odczytujemy na osi OX –

są to wszystkie x dla których istnieje wykres.

Wykres tej funkcji kończy się „kółeczkami”

więc jej dziedzina to przedział: D

f

= [-6, 5].

PRZYKŁADOWE ZADANIA.

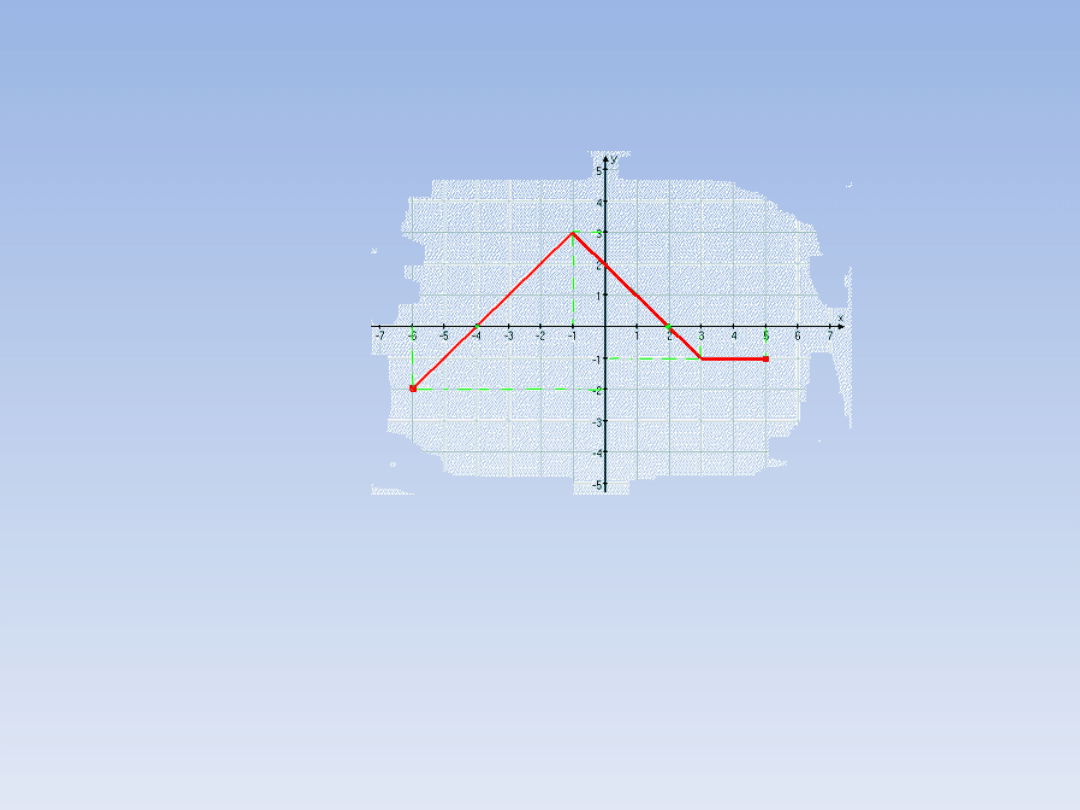
Zadanie 1 – ciąg dalszy.

-Zbiór wartości odczytujemy na osi OY – to
wszystkie y dla których istnieje wykres.
ZW

f

= [-2, 3].

PRZYKŁADOWE ZADANIA.

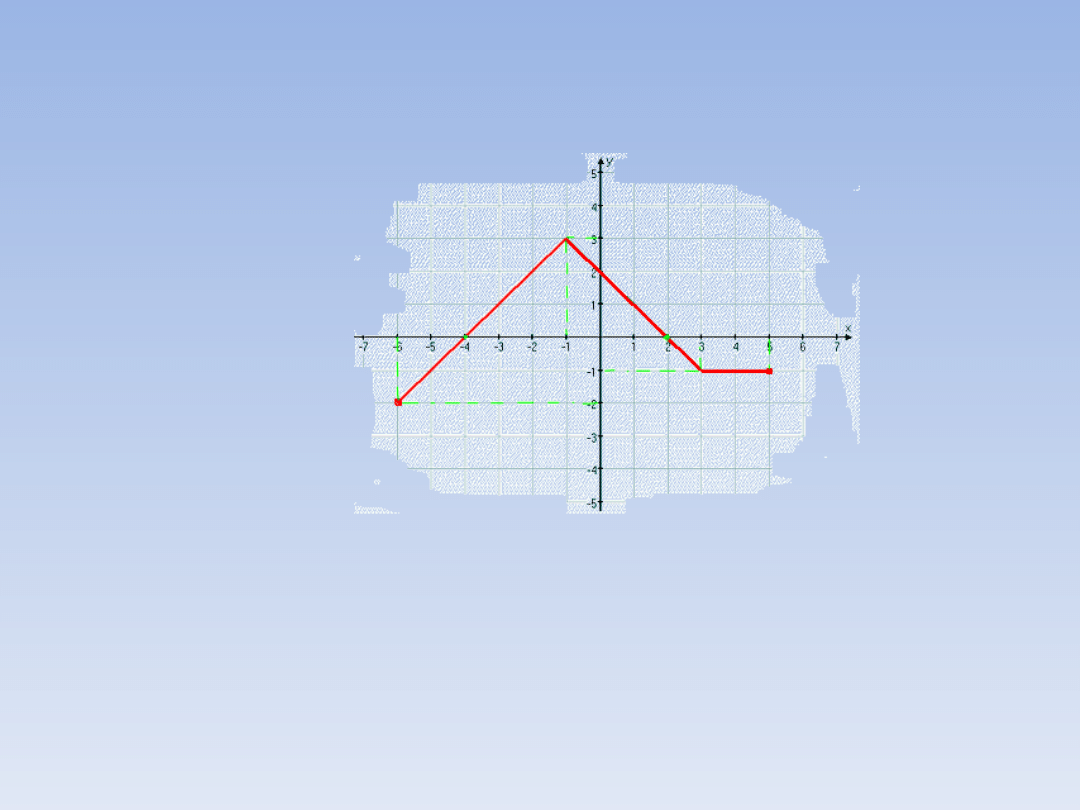
Zadanie 1 – ciąg dalszy.

-Miejsca zerowe to te x w których wykres
przecina oś OX, mamy więc: x = -4 i x = 2.
- Funkcja jest rosnąca w przedziale [-6, -1),
malejąca w przedziale (-1, 3), stała w
przedziale (3, 5].

PRZYKŁADOWE ZADANIA.

Zadanie 1 – ciąg dalszy.

-Funkcja ta przyjmuje wartości ujemne dla x
 (-6, -4) oraz dla x  (2, 5]. Wartości

dodatnie funkcja przyjmuje dla x  (-4, 2).
- Największa wartość tej funkcji to y

max

= 3.

Najmniejsza wartość funkcji to y

min

= -2.