30. Prawo Kulomba

głosi, że siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych jest wprost proporcjonalna do iloczynu ładunków i odwrotnie proporcjonalna do kwadratu odległości między ich środkami. Jest to podstawowe prawo elektrostatyki.

Prawo to można przedstawić za pomocą wzoru:

,

w którym:

F - siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych,

Q₁, Q₂ - punktowe ładunki elektryczne,

r - oddalenie między ładunkami,

k - współczynnik proporcjonalności:

przy czym:

gdzie:

ε - przenikalność elektryczna ośrodka,

ε_r - przenikalność elektryczna względna ośrodka (stała dielektryczna),

ε₀ - przenikalność elektryczna próżni.

Jednostka ładunku elektrycznego, także nazwana na cześć Kulomba (Charlesa Coulomba), jest równa połączonym ładunkom 6,24 x 10¹⁸ protonów (lub elektronów).

Z prawa tego wynika m.in, że:

Im większy ładunek będą posiadały przedmioty, tym między nimi będzie większa siła; także im większa odległość będzie między przedmiotami, tym mniejsza siła będzie między nimi.

Jeśli stykają się z sobą dwa naładowane przedmioty o takiej samej pojemności, dzielą między siebie ładunek po równo. Dla przykładu załóżmy, że jeden przedmiot ma ładunek +4 kulombów, a drugi +8 kulombów. Kiedy się zetkną, ładunek będzie przepływał od 8-kulombowego obiektu do 4-kulombowego, dotąd aż oba przedmioty osiągną ładunek +6 kulombów. Jeżeli pierwotnie obydwa przedmioty posiadały by ładunek +6 kulombów, między nimi nie przepłynął by żaden ładunek.

Jeżeli dwa przedmioty mają różne pojemności, dzielą ładunki proporcjonalnie do ich pojemności. Jeśli przedmiot o pojemności 10 faradów dotknie przedmiotu o pojemności 5 faradów, 10-faradowy przedmiot będzie miał dwa razy większą ilość ładunków niż przedmiot 5-faradowy (bo 2x5=10). Załóżmy, że przedmioty są przeciwnie naładowane, pierwszy ma ładunek +20 kulombów, a drugi -8 kulombów. Ich całkowity ładunek wynosi +12 kulombów. Po ich zetknięciu, 10 faradowy przedmiot będzie miał ładunek +8 kulombów, a 5-faradowy przedmiot będzie miał ładunek +4 kulombów.

Prawo to opublikował w 1785 Charles Augustin de Coulomb

31. Zasada superpozycji pól elektrostatycznych:

natężenie pola wytwarzanego przez układ ładunków (jeśli jest to rozciągłe źródło to należy je podzielić na tak małe części aby mogły być uważane za punktowe)jest równe wektorowej sumie natężeń pól wytwarzanych przez każdy ładunek z osobna. Siła Coulomba: Siła oddziaływania dwóch ładunków q₁ i q₂

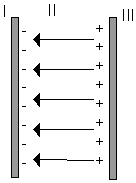
F = k ; gdzie stała k = ; Współczynnik ε₀ = 8.854·10^-12 C²/(Nm²) nosi nazwę przenikalności elektrycznej próżni. W układzie cgs k = 1. Natężenie pola elektrostatycznego od ładunku punktowego lub b. małej kuli: φEdS = E(4πr²) Zgodnie z prawem Gaussa: E(4πr²) = Q/ε₀ ; czyli: E = = k; Pole od dwóch nieskończenie jednorodnie naładowanych płaszczyzn (kondensator płaski). Pole wytwarzane przez płytę "po lewej stronie" (rysunek poniżej) jest równe E_minus = σ/2ε₀ i skierowane ku płycie. Pole wytwarzane przez płytę po prawej E_plus = σ/ε₀ i skierowane jest od płyty. Zatem w obszarze I: E_I = σ/2ε₀ + (- σ/2ε₀) = 0 ; w obszarze II: E_II = -σ/2ε₀ + (- σ/2ε₀) = -σ/ε₀ ; w obszarze III: E_III = (- σ/2ε₀) + σ/2ε₀ = 0

32. Natężenie i POTENCJAŁ pola elektrycznego

Natężenie jest wielkością wektorową. Wzór na natężenie pola E=F:Q. Stałe pole elektryczne występuje gdy przez przewodnik płynie prąd elektryczny. Zmienne pole elektryczne występuje zawsze wraz ze zmiennym polem magnetycznym - wywołują siebie nawzajem i są nierozłączne, określa się je ogólnie jako pole elektromagnetyczne.

Potencjał pola elektrycznego. Jest to energia potencjalna pola elektrycznego przypadająca na jednostkę ładunku:

Oznaczenia

V - potencjał; e _P - energia potencjalna; k - stała elektrostatyczna;

Q - ładunek źródłowy; q - ładunek elementarny; r - odległość punktu od źródła;

33. Twierdzenie Ostrogradskiego-Gaussa

Niech
będzie obszarem ograniczonym powierzchnią zamkniętą S, a P(x, y, z), Q(x, y, z) i R(x, y, z) będą funkcjami posiadającymi ciągłe pochodne cząstkowe pierwszego rzędu na obszarze V. Prawdziwa jest wówczas następująca zależność:

Przy czym całka po lewej stronie jest po zewnętrznej stronie powierzchni S.

Uwagi Twierdzenie Ostrogradskiego-Gaussa często zapisujemy w postaci wektorowej:

Niech A będzie polem wektorowym, dla którego istnieje dywergencja na całym obszarze V:

Zaletą wzoru zapisanego w ten sposób jest jego zwięzłość.

Twierdzenie Ostrogradskiego-Gaussa umożliwia nam zamianę całki powierzchniowej na objętościową (potrójną) i na odwrót, w zależności od potrzeb. Stosowane jest również często w elektrodynamice teoretycznej.

34. Dielektryki:

Umieszczenie materiału nieprzewodzącego między okładkami kondensatora powoduje zwiększenie pojemności od wartości C do wartości C'. κ = gdzie κ jest względną przenikalnością elektryczną (stałą dielektryczną). Dipol: dwa identyczne ładunki o przeciwnych znakach umieszczone w odległości 2a. W jednorodnym polu elektrycznym: Elektryczny moment dipolowy p = 2aq (2a - odległość między ładunkami, q - ładunek) ma kierunek od „-”do „+” . Moment dipolowy tworzy z liniami pola elektrycznego kąt θ. Na dipol działają dwie równe siły F i -F , F = qE. Istnieje wypadkowy moment obracający dipol wokół osi przechodzącej przez p. 0 równy τ = 2aFsinθ. Po podstawieniu mamy: τ = 2aqEsinθ = pEsinθ Widać że na dipol umieszczony w zewnętrznym polu E działa moment skręcający dążący do ułożenia go wzdłuż linii pola. Polaryzacja dielektryka(indukcja elektrostatyczna): jeżeli dielektryk zostaje umieszczony w polu elektrostatycznym to pod wpływem tego pola elektrony mogą zostać przesunięte jedynie w obrębie cząstek. Wektor polaryzacji: wiąże się wyłącznie z ładunkiem polaryzacyjnym. Jego linie zaczynają się i kończą na ładunkach polaryzacyjnych.

35. TEORIA ELEKTRONOWA PRZEWODNICTWA

Na czym polegała pierwsza teoria elektronowa Drudego?

Teoria ta opracowana w 1900 r. opierała się na założeniu, że elektrony wartościowości t.zn. elektrony zlokalizowane na ostatniej orbicie o największej liczbie kwantowej n odrywają się od atomów tworzących skondensowany stan skupienia i poruszają się między jonami podobnie do drobin gazu w zbiorniku. Stąd powstało pojęcie gazu elektronowego, który zgodnie z założeniem miał podlegać prawom kinetycznej teorii gazów. Teoria ta zakładała równomierny rozkład ładunków dodatnich i barierę energetyczną na powierzchni metalu utrudniającą wyjście elektronów na zewnątrz. Głównym sukcesem teorii Drudego było obliczenie stałej Lorenza w prawie Wiedemenna-Franza, które mówi, że stosunek przewodnictwa cieplnego do elektrycznego jest proporcjonalny do temperatury bezwzględnej. Teoria ta nie potrafiła jednak wyjaśnić ciepła właściwego, które na podstawie tej teorii było zawyżone. Podstawowe założenia teorii Drudego zostały przejęte przez nowsze, zmodyfikowane teorie.

36. Pole magnetyczne:

własność przestrzeni, w której na umieszczone w niej magnesy, przewodniki z prądem i poruszające się ładunki działają siły magnetyczne. Istnieje ono wokół przewodników z prądem, wokół magnesów stałych i wokół poruszającego się ładunku.

Linie pola magnetycznego - krzywe, do których styczne w każdym punkcie pokrywają się z kierunkiem indukcji magnetycznej. Jeden z pokazów dotyczył 2 równoległych przewodów, w zależności od kierunku prądu odpychały się lub przyciągały. Własności linii pola magnetycznego: biegną od N do S, są to krzywe zamknięte, ich ilość świadczy o indukcji, można je wystawić w każdym punkcie pola, brak źródła, nie można rozdzielić pola magnetycznego. Prawo Ampera: Krążenie wektora indukcji po dowolnej krzywej zamkniętej jest proporcjonalne do sumy natężeń prądów zawartych wewnątrz tej krzywej : I - natężenie prądu; ΔL - długość krzywej zamkniętej; B - natężenie pola elektromagnetycznego (indukcja); μ₀ - przenikalność magnetyczna próżni; j - ilość natężeń (przewodników); i - ilość odcinków krzywej (Prawo Ampera służy do wyznaczania indukcji pola magnetycznego pochodzącego z różnych przewodników z prądem.) Doświadczenie Oersteda: Opiłki metalu rozsypane na kartce układają się w okręgi wokół przechodzącego przez kartkę przewodnika z prądem.

37. Zastosowanie prawa Biota-Savarta:

Pozwala obliczyć B z rozkładu prądu. To prawo i prawo Ampera muszą być matematycznie równoważne. Prawo Ampera jest jednak "łatwe" w stosowaniu tylko gdy rozkłady prądów są na tyle symetryczne, że obliczenie odpowiedniej całki nie jest trudne. Gdy rozkład prądów jest skomplikowany (nie znamy jego symetrii) to dzielimy prądy na nieskończenie małe elementy i stosując prawo Biota-Savarta obliczamy pole od takich elementów, a następnie sumujemy je (całkujemy) żeby uzyskać wypadkowy wektor B. Wartość liczbowa dB zgodnie z prawem Biota-Savarta wynosi: dB = a zapisane w postaci wektorowej dB = ; Obliczmy pole B na osi kołowego przewodnika z prądem. Z prawa B -S otrzymujemy: dB = oraz dB_II = dBcosα

Z tych równań otrzymujemy: dB = ; Ponadto: r = oraz cosα = = ; Podstawiając otrzymujemy: dB = dl

Zauważmy, że wielkości I, R, x są takie same dla wszystkich elementów prądu.

Całkujemy, żeby obliczyć B (wyłączając stałe czynniki przed znak całki)

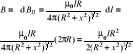
Dla x >> R dostajemy: B =

38. PRAWO AmperE'a:

Wartość całki okrężnej wektora natężenia pola magnetycznego, wytworzonego przez stały prąd elektryczny w przewodniku wzdłuż linii zamkniętej otaczającej prąd, jest równa sumie algebraicznej natężeń prądów obejmowanych przez tę linię.

Indukcja wokoło przewodnika prostoliniowego: B = ; R - odległość danego punktu od przewodnika. Indukcja w środku solenoidu: B = ; n - ilość zwojów; L - długość solenoidu. Indukcja w środku 1 zwoju : B = ; R - promień zwoju;

40. ODDZIAŁYWANIE WZAJEMNE PRZEWODNIKÓW Z PRĄDEM

Dwa równoległe przewodniki z prądem oddziałują na siebie. Jeśli zwroty prądów są zgodne, to przewodniki przyciągają się. Jeśli zwroty prądów są przeciwne, to przewodniki odpychają się.

Siłę możemy obliczyć ze wzoru:

Jeśli w obu przewodnika płynie jednakowy prąd, to wzór się upraszcza do postaci:

gdzie:

μ₀ - przenikalność magnetyczna próżni

μ₀ = 4π10^-7 N/A²

Zjawisko oddziaływania wzajemnego dwóch przewodników z prądem zostało wykorzystane do definicji jednostki natężenia prądu - ampera.

Natężenie prądu w przewodniku wynosi jeden amper wtedy, gdy siła wzajemnego przyciągania dwóch długich równoległych przewodników odległych od siebie o jeden metr przypadająca na jednostkę długości (1 m) wynosi 2*10^-7 N/m.

41. Ruch ładunku w polu magnetycznym

W elektrostatyce dowiedzieliśmy się, iż na ładunek w polu elektrostatycznym działa siła niezależnie od tego czy ładunek porusza się, czy nie. Sprawdźmy czy tak samo jest w polu magnetycznym.

Na ładunek w polu magnetycznym działa siła Lorentza.
_ _ _
F=q(VxB)

V - prędkość ładunku
B - indukcja pola

F=qVBsinα - wartość siły

Rozważmy cztery przypadki w polu jednorodnym:

• I przypadek - ładunek spoczywa
  
  
  
  
  Spoczywający ładunek nie podlega sile Lorentza (F=0).

• II przypadek - ładunek porusza się zgodnie z liniami pola
  
  
  
  
  Ładunek porusza się ruchem jednostajnym prostoliniowym, zachowując początkową prędkość równoległą do linii pola (F=0).

• III przypadek - ładunkowi nadaje się prędkość początkową o kierunku prostopadłym do linii pola
  
  
  
  
  Na ładunek działa siła Lorentza. F=qVB
  
  Zwrot tej siły prowadzi za rysunek. Wyznacza się go za pomocą reguły Fleminga lub reguły lewej ręki. Taka siła nie powoduje zmiany wartości prędkości, lecz zakrzywia tor ruchu (ładunek zacznie poruszać się po okręgu). Jest więc siłą dośrodkową.

• IV przypadek - ładunek wpada do pola magnetycznego pod kątem
  
  
  
  
  
  Ruch tego ładunku można traktować jako złożeniu II-go i III-go przypadku. Ładunek będzie się poruszał po linii śrubowej.
  F=qVBsinα

42. Ruch ładunków w polu elektrycznym.

1) ładunek porusza się równolegle do linii pola.

Ładunek będzie się poruszał ruchem prostoliniowym jednostajnie przyspieszonym.

Przyspieszenie:

Jednocześnie ulegnie zmianie energia kinetyczna ładunku:

Oznaczenia

U - różnica potencjałów, jaką przebył ładunek; q - ładunek; E - natężenie pola; e _K - energia kinetyczna; e ₀ - energia początkowa ładunku;

a - przyspieszenie; m - masa ładunku;

2) ładunek wpada pod kątem prostym do linii pola.

Torem ładunku jest parabola.

;
;

,

Oznaczenia

U - różnica potencjałów, jaką przebył ładunek; q - ładunek; E - natężenie pola; e _K - energia kinetyczna; e ₀ - energia początkowa ładunku; a - przyspieszenie; m - masa ładunku;

V - prędkość; T - czas; oraz oznaczenia na rysunku.

44. Indukcja elektromagnetyczna.

Jest to przyczyna pojawienia się prądu w obwodzie bez źródła prądu, gdy nastąpi zmiana strumienia pola elektromagnetycznego.

Prawo Faradaya dla przewodnika. ε = - ; Siła elektromotoryczna indukcji ε jest równa zmianie strumienia pola magnetycznego Δφ przez przyrost czasu Δt w którym ta zmiana nastąpiła. Prawo Faradaya jest zasadą zachowania energii. Reguła Lenza: Prąd indukowany ma taki kierunek, że wytworzone przez niego pole magnetyczne przeciwstawia się przyczynie, która go wywołała. Kierunek prądu indukowanego w pętli zależy od tego czy strumień rośnie czy maleje (zbliżamy czy oddalamy magnes). Ta reguła dotyczy prądów indukowanych.

45. Zjawisko samoindukcji:

Podczas otwierania i zamykania obwodu z prądem mamy do czynienia ze zmianą strumienia pola magnetycznego i - zgodnie z prawem indukcji Faradaya - w obwodzie pojawi się siła elektromotoryczna samoindukcji. W obwodzie popłynie krótkotrwały prąd indukcyjny : ε_­SI = -L ; L = - ; [= H(henr)]

1 henr to indukcyjność takiego obwodu, w którym przy zmianie natężenia prądu o 1 A w czasie 1 s powstanie ε o wartości 1 V. ε_SI - siła elektromotoryczna samoindukcji; I - natężenie prądu elektrycznego przy zwarciu; T - czas; L - współczynnik samoindukcji (cecha charakterystyczna zwojnicy); μ₀ - przenikalność magnetyczna próżni; n - ilość zwojów; s - pole powierzchni; l - długość zwojnicy ; Indukcja wzajemna: Jeżeli ustawimy dwie cewki w taki sposób że strumień magnetyczny wytwarzany przez prąd w jednej przenika przez zwoje drugiej to w przypadku zmian natężenia prądu w pierwszej w drugiej zostanie wyindukowana siła elektromotoryczna indukcji wzajemnej ε_ind : ε_ind = -M

46. Równania Maxwella i ich sens fizyczny.

Prawa Maxwella są podstawowymi prawami, które łączą zjawiska elektryczne i magnetyczne.

I Prawo Maxwella

Zmienne pole elektryczne wytwarza wirowe pole magnetyczne. - krążenie wektora indukcji magnetycznej po dowolnej krzywej zamkniętej jest proporcjonalne do pochodnej (po czasie) strumienia natężenia pola elektrycznego przepływającego przez powierzchnię rozpiętą na tej krzywej.

Ogólnie sformułowanie pierwszego prawa Maxwella zawiera też prawo Ampere'a

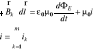
i - sumaryczne natężenie prądów przepływających przez powierzchnię rozpiętą na danej krzywej.

II Prawo Maxwella

Zmienne pole magnetyczne wytwarza wirowe pole elektryczne.- krążenie wektora natężenia pola elektrycznego po dowolnej krzywej zamkniętej jest równe pochodnej (po czasie) strumienia indukcji magnetycznej przepływającego przez powierzchnię rozpiętą na tej krzywej.

47. Fale elektromagnetyczne:
W 1865 roku Maxwell w swojej teorii elektromagnetyzmu przewidział dwa zjawiska, które nazywamy prawami Maxwella:

I prawo Maxwella - Zmienne pole magnetyczne powoduje powstanie wirowego (i też zmiennego) pola elektrycznego.

II prawo Maxwella - Zmienne pole elektryczne wytwarza wokół siebie wirowe (i też zmienne) pole magnetyczne.
Wystarczy w jakikolwiek sposób wytworzyć zmienne pole (np. magnetyczne) i to spowoduje rozchodzenie się pola elektrycznego i magnetycznego. Takie rozchodzące się pole elektromagnetyczne nazywamy falą elektromagnetyczną.
Prędkość V rozchodzenia się fali elektromagnetycznej w próżni jest równa prędkości światła w próżni.



Równość ta nasunęła Maxwellowi wniosek, iż światło jest jednym z rodzajów fal elektromagnetycznych.


Powyższy wykres przedstawia przestrzenny obraz rozkładu natężenia pola elektrycznego i indukcji pola magnetycznego - fali elektromagnetycznej rozchodzącej się w kierunku x. Wynika z niego, iż fala elektromagnetyczna jest falą poprzeczną, przy czym jej długość jest określona wzorem:


T - okres drgań źródła fali

Uwzględniając wzór na częstotliwość fali, otrzymujemy:

48. REZONANS ELEKTROMAGNETYCZNY

Znasz zjawisko rezonansu mechanicznego i akustycznego. Wiesz również jakie warunki muszą być spełnione, aby drgania wysyłane przez jedno ciało drgające zostało „odebrane” przez drugie ciało. Sprawdzimy czy zjawisko rezonansu zachodzić będzie w przypadku dwóch obwodów drgających.

Jeden z obwodów musi być zasilany z zewnętrznego źródła energii, aby uzupełniać straty. W drugim natomiast musi istnieć możliwość zmiany pojemności kondensatora lub współczynnika indukcji własnej obwodu, czyli musi mieć możliwość zmiany okresu drgań własnych tego obwodu (rys. 51).

Rys. 51. Schemat obwodów do pokazu rezonansu elektromagnetycznego.

Jeżeli pierwszy obwód pobudzimy do drgań, to zmieniając okres drgań własnych drugiego obwodu doprowadzimy do pojawienia się drgań elektrycznych w obwodzie drugim (z prawej strony rys. 51). Obwody elektryczne mogą więc przekazywać sobie energię wtedy, gdy okres drgań T₁ obwodu przekazującego energię jest równy okresowi drgań własnych T₂ obwodu, który ją odbiera. Opisane wyżej zjawisko nazywamy rezonansem elektromagnetycznym, a jego spełnienie jest uwarunkowane równością okresów drgań własnych dwóch obwodów, czyli

T₁ = T₂

Na podstawie równania 24 możemy zapisać, że_{_______ ________}

2 • л • √L₁ • C₁ = 2 • л • √L₂ • C₂

a zatem

L₁ • C₁ = L₂ • C₂

czyli iloczyn pojemności kondensatora C I indukcyjności zwojnicy L dla danych dwóch elektrycznych obwodów drgających jest wielkością stałą. 

Jak odbywa się przekazywanie energii między obwodami? Odpowiedź na to pytanie znajdziesz w dalszej części tej lekcji.

49. WIDMO FAL ELEKTROMAGNETYCZNYCH

50. Model budowy atomu Rutherforda (1911)
Elektrony krążą wokół jądra atomowego jak planety wokół Słońca Atom jest elektrycznie obojętny W atomie liczba protonów jest równa liczbie elektronów Jądro atomowe ma ładunek dodatni Elektrony maja ładunki ujemne Liczba neutronów w jądrze (oprócz wodoru) jest równa lub większa od liczby protonów. Miedzy protonami i neutronami działają siły jądrowe. Dośrodkowa siła elektrostatyczna trzyma elektrony na uwięzi w atomie.

Modele budowy atomu: 1. Model Rutherforta - atomy przypominają miniatury układu słonecznego, elektrony poruszają się wokół jądra: A) jądro, B) elektron. 2. Model Bohra - aby wyjaśnić stabilność atomu wprowadza pojęcie skwantowanych orbit elektronów: A) jądro, B) elektron, C) orbita elektronu.

51. MODEL ATOMU BOHRA
W modelu atomu według Bohra elektrony krążą po orbitach tzw. powłoki. Elektrony mogą przeskakiwać z powłoki na powłokę. Przy zmianie powłoki następuje zmiana energii elektronu. Energia elektronu rośnie wraz z odległością od jądra. Stan o większej energii jest stanem nietrwałym - nazywamy go stanem wzbudzonym. Zmiana energii elektronu w atomie zachodzi w sposób kwantowy (skokowy). W skład jądra atomowego wchodzą protony i neutrony. Liczba atomowa Z równa jest liczbie protonów w jądrze. Liczba Z równa jest liczbie porządkowej pierwiastka w układzie okresowym Liczba elektronów w atomie równa jest liczbie protonów w jądrze. Liczba masowa A atomu równa jest sumie ilości protonów i ilości neutronów w jądrze atomu. A = Z + N czyli N = A - Z, gdzie N oznacza liczbę neutronów w jądrze.

52. ENERGIA ELEKTRONU W ATOMIE

Energia stanów stacjonarnych atomu wieloelektronowego zależy od n, l, m_l, m_s. W podstawowym stanie energetycznym wszystkie elektrony przyjmują najniższe możliwe poziomy energetyczne. Struktura poziomów energetycznych, a także widm atomowych, wykazuje wyraźne prawidłowości na tle okresowego układu pierwiastków. Atomy pierwiastków należących do tej samej kolumny układu okresowego charakteryzują się takim samym układem poziomów energetycznych i podobną strukturą widma.

Jeżeli chcemy np. spowodować przejście elektronu z jednej powłoki na inną, o wyższej energii, musimy dostarczyć mu porcji (kwantu) energii równej dokładnie różnicy jaka istnieje między energiami tych dwóch powłok. Musi to być jednorazowa porcja - elektron nie może pobierać i kumulować drobniejszych porcji, bowiem nie może istnieć w stanie energetycznym pomiędzy poziomami dozwolonymi. Innymi słowy, zmiany energii poszczególnych elementów mikroświata nie mogą odbywać się "na raty" a jedynie jednym, ściśle określonym aktem pochłonięcia porcji (kwantu) energii. Jeżeli energie poziomu 1 i 2 wynoszą odpowiednio E₁ i E₂, a E₂ - E₁ = δ, to aby przenieść elektron ze stanu 1 w stan 2 należy dostarczyć mu porcji energii (kwantu) równej δ, zaś elektron samoistnie przechodząc ze stanu 2 do stanu 1 wyemituje porcję energii równą δ. 

Tu pora na sformułowanie jeszcze jednej generalnej zasady mikroświata - elementy mikroświata dążą (co nie oznacza, że zawsze osiągają !) do osiągnięcia najniższej możliwej w danych warunkach energii, oraz samorzutnie dążą do uzyskania najwyższej wartości entropii, czyli jak najbardziej równomiernego rozpowszechnienia w całym wszechświecie. 

53. Budowa i skład jądra atomowego

Jądro atomowe jest to centralna część atomu składająca się z nukleonów powiązanych siami jądrowymi. Jądro atomowe określa się przez podanie liczby masowej A ( liczby nukleonów 0 oraz liczby atomowej Z ( liczby protonów ).

Z - liczba protonów ; A - Z - liczba neutronów ; A - ilość wszystkich składników j. atomowego ( liczba masowa)

Jądro o określonej wartości A i Z nosi nazwę - NUKLIDU.

Istnieją jądra , które mają ten sam ładunek ( taką samą liczbę protonów ) , ale różnią się liczbą neutronów nazywamy IZOTOPAMI

Są to izotopy ( tego samego pierwiastka )

Izotop wodoru

deuter

tryt

54. CZĄSTKI ELEMENTARNE

obiekty, których istnienie i wzajemne oddziaływanie pozwala wyjaśnić formy występowania i zachowania się materii. W węższym znaczeniu do cząstek elementarnych zalicza się obiekty nie mające struktury wewn.: leptony, kwarki oraz bozony pośredniczące w oddziaływaniach; w szerszym znaczeniu (hist.) — wszystkie cząstki subjądrowe. Cząstki elementarne są źródłami pól (pole fizyczne), za pośrednictwem których oddziałują między sobą. Znane są 4 rodzaje oddziaływań: silne, słabe, elektromagnet. i grawitacyjne. Ze względu na oddziaływania, w których uczestniczą, cząstki elementarne będące źródłami pól dzieli się na hadrony (biorą udział we wszystkich oddziaływaniach, są zbud. z kwarków, np. proton z kwarków uud, neutron — ddu, mezon K⁺ — u
, K^- — ūs;
, ū — antykwarki) oraz leptony (nie biorą udziału w oddziaływaniach silnych). Większość znanych cząstek elementarnych jest nietrwała, rozpada się w czasie krótszym niż 10^-6 s, najkrócej żyjące cząstki, tzw. rezonanse, mają czas życia rzędu 10^-21 -10^-24 s. Rozmiary cząstek elementarnych są rzędu 10^-15 m (hadrony) lub mniejsze niż 10^-17 m (leptony). Masy cząstek elementarnych są zawarte między 0,51 MeV (elektron) a 11,02 GeV (mezon Y). Ładunki cząstek elementarnych są skwantowane i wynoszą -2e, -e, 0, e, 2 e (ładunki kwarków -1/3e, +2/3 e, odpowiednich antykwarków odwrotnie), gdzie e jest ładunkiem elektronu. Cząstki elementarne o spinie połówkowym nazywa się fermionami — należą do nich leptony i bariony, zaś cząstki elementarne o spinie całkowitym — bozonami, do których należą mezony. Oddzielną grupę cząstek elementarnych stanowią cząstki przenoszące oddziaływania (kwanty oddziaływania). Cząstkami takimi są: foton — przenoszący oddziaływania elektromagnet., grawiton — kwant oddziaływań grawitacyjnych, bozony W^±, Z ⁰ — bozony pośredniczące oddziaływań słabych, oraz gluony — kwanty oddziaływań silnych. Grawiton powinien mieć spin 2, pozostałe kwanty oddziaływań mają spin 1. Foton znany jest od dawna; 1983 odkryto bozony W^± i Z⁰, również istnienie gluonów uważa się obecnie za udowodnione na podstawie wyników doświadczeń nad oddziaływaniem cząstek elementarnych; istnienie grawitonu jest b. prawdopodobne.

Źródłem informacji o cząstkach elementarnych jest badanie zderzeń cząstek elementarnych przy wysokich energiach. Źródłem wysokoenerg. cząstek są akceleratory cząstek naładowanych oraz promieniowanie kosmiczne. Głównymi ośr. badań cząstek elementarnych rozporządzającymi akceleratorami o najwyższych energiach są: Fermi National Accelerator Laboratory w Batavii (USA), Eur. Centrum Badań Jądr. (CERN) w Genewie, Ośr. Badań Jądr. w Sierpuchowie, Deutsches Elektronen-Synchrotron (DESY) w Hamburgu oraz Stanford Linear Accelerator Center (SLAC) w Stanford. Pierwszą odkrytą cząstką elementarną był elektron (J.J. Thomson, 1897); do 1932 jedynymi znanymi cząstkami elementarnymi, oprócz elektronu, były foton i proton. Od 1932, kiedy został odkryty neutron (J. Chadwick) i pozyton (C.D. Anderson), datuje się szybki rozwój badań nad cząstkami elementarnymi, a w jego następstwie — odkrycie mezonów, hiperonów, neutrin i wielu antycząstek.

---