ZASTOSOWANE ODWZOROWANIA KONFOREMNYCH

WYKŁAD (wersja 1.02)

1. FUNKCJA ŻUKOWSKIEGO

Jedną z możliwych Funkcję odwzorowujących, transformującą zewnętrze okręgu na zewnętrze innego konturu zamkniętego (np. profilu lotniczego) stanowi można przedstawić w postaci szeregu Laurenta:

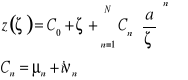
(1)

Jeżeli ograniczymy się do n=1, przyjmując: C₀=0, C₁=a otrzymamy tzw. funkcję Żukowskiego (N.E. Żukowski, 1905):

(2)

Przekształćmy funkcję Żukowskiego do wygodniejszej postaci:

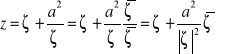
(3)

W ogólnym przypadku:

(4)

Rys. 1. Płaszczyzna kanoniczna i płaszczyzna fizyczna x0y

1. Płaska płytka

Rozpatrzmy funkcję Żukowskiego, dla ζ₀=0 i R = a

Wówczas mamy natychmiast:

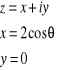
(5)

Rys. 2. Odwzorowanie koła na cięcie

Zatem zewnętrze okręgu zostało odwzorowane na płaszczyznę z cięciem o długości 4a

2. Elipsa

Z kolei rozpatrzymy funkcję Żukowskiego, dla ζ₀=0 i R > a

Po prostych przekształceniach otrzymamy równanie elipsy:

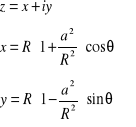
(6)

Grubość względna tego profilu eliptycznego wynosi:

lub:

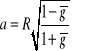
Rys. 3. Odwzorowanie koła na elipsę

3. Profile Żukowskiego

W przykładowych obliczeniach założono, że parametr a ma stałą wartość: a=0,25

Założono również, że, wartości a i R nie są niezależne, a powiązane przez zależności trygonometryczne wiążące ze sobą położenie środka odwzorowanego okręgu i tzw. kąt spływu w ostrzu (patrz dalej). Z uwago na złożoność wzorów końcowych, warto jest przeprowadzić obliczenia obliczając wyniki pośrednie.

Z Rys. 1. wynikają następujące zależności geometryczne:

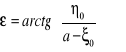
(7)

(8)

Teraz możemy zdefiniować współrzędne na płaszczyźnie kanonicznej (Rys 1. z lewej):

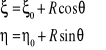
(9)

Zatem, wartości współrzędnych profilu przyjmą wartości:

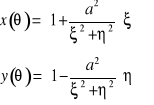
(10)

Ze względu na warunek Kutty-Żukowskiego (o czym dalej) o spływie w ostrzu obliczenia warto zacząć od współrzędnej kątowej ε:

(11)

Poniżej zostały podane przykłady obliczeń geometrii profili Żukowskiego.

1.3.1. Łuk kołowy

Rozpatrzymy teraz przypadek R>a i ζ₀=iη₀

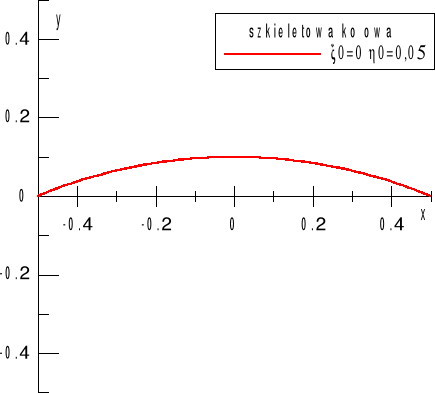
Rys. 4. Szkieletowa kołowa, a=0,25

Otrzymujemy wówczas profil o zerowej grubości i będący łukiem koła.

1.3.2. Profil symetryczny- „ster Żukowskiego”

Następny przypadek to: ξ₀>0 η₀=0 R>a

Otrzymujemy wówczas formę symetryczną, podobną do przedstawionej na Rys. 5.

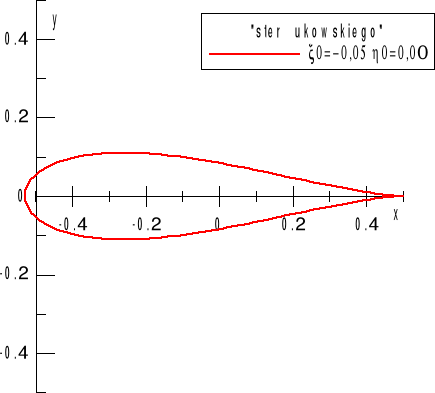
Rys. 5. „Ster Żukowskiego”, a=0,25

1. Asymetryczny profil Żukowskiego

Wariant najbardziej ogólny czyli: ξ₀<0 η₀<0 R>a

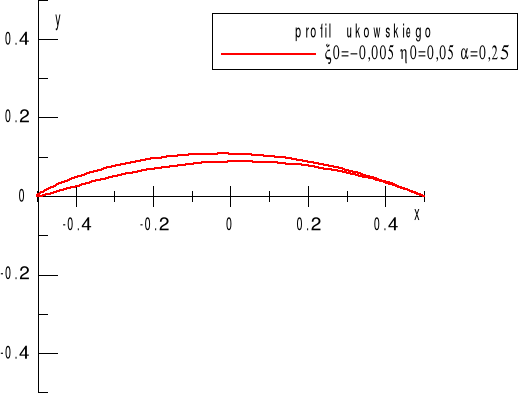
Rys. 6. Profil Żukowskiego o małej grubości a=0,25

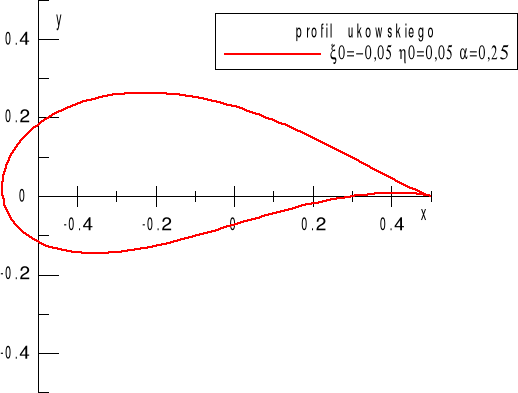
Rys. 7. Profil Żukowskiego (bardzo) gruby, a=0,25

Z powyższych obliczeń widać (Rys. 4…7), że dla profili cienkich cięciwa jest, w przybliżeniu 4 razy większa niż parametr a:

(12)

Generalizując, można powiedzieć, że współrzędna ξ₀ odpowiada za grubość profilu, natomiast η₀ za jego wysklepienie.

2. Prędkości na powierzchni profilu

2.1. Postulat Kutty-Żukowskiego:

Prędkość zespolona na powierzchni profilu walca, wyrażona jako pochodna potencjału zespolonego F jest równa:

(13)

a prędkość na profilu:

(14)

Prędkość na powierzchni walca daje się wyrazić jako:

(15)

Zatem, uwzględniając, że:

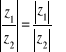
(16)

możemy napisać:

(17)

Ponieważ jedyną składową jest składowa styczna do powierzchni profilu, więc powyższa zależność pozwala wyznaczyć rozkład ciśnienia (lub współczynnika ciśnienia) na powierzchni profilu.

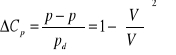
(18)

Kluczowe znaczenie ma zatem wyznaczenie pochodnej funkcji odwzorowującej.

(19)

Wprowadzamy zmienne pomocnicze μ, ν:

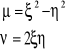
(20)

Zatem:

(21)

A moduł pochodnej:

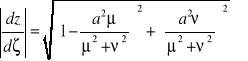
(22)

Prędkość wyznaczymy na podstawie warunku Kutty-Żukowskiego o spływie w ostrzu:

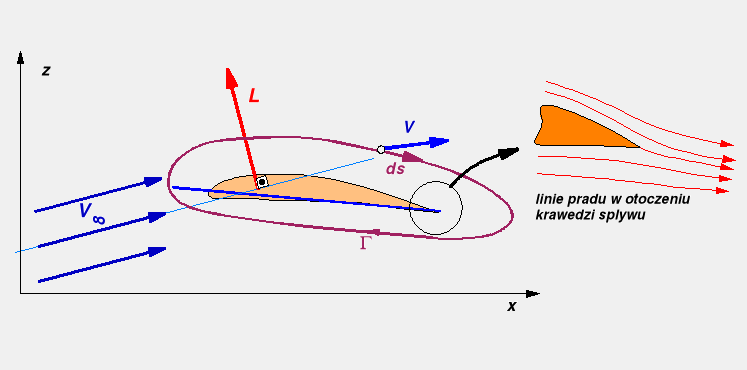
Rys. 8. Warunek Kutty-Żukowskiego

Którego sens fizyczny sprowadza się, do zachowania styczności przepływu do powierzchni w punkcie kątowym na profilu odpowiadającym tylnemu punktowi spiętrzenia przy opływie walca kołowego. Punkt ten ma współrzędną kątową ε Jednoznaczna lokalizacja punktu spiętrzenia pozwala na wyznaczenie wartości cyrkulacji na profilu.

2.2. Bezcyrkulacyjny i cyrkulacyjny opływ walca kołowego płynem idealnym

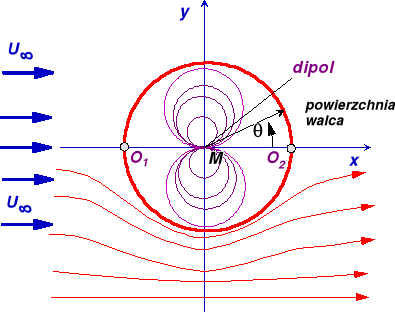
Rys. 9. Opływ walca jako superpozycja przepływu płasko-równoległego i dipola

Opływ symetryczny walca można przedstawić jako złożenie przepływu płasko-równoległego i przepływu wywołanego momentem dipolowym M

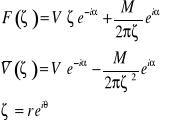
(23)

Rys. 10. Prędkości styczne

Uwzględniając fakt, że:

(24)

dostajemy:

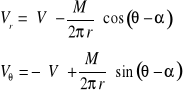
(25)

Prędkość normalna na powierzchni walca r=R powinna być równa zeru. Stąd wynika wartość momentu dipolowego:

(26)

Stąd prędkość styczna jest równa:

(27)

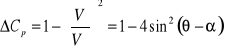
(28)

Minimalna wartość ΔC_pmin=-3, dla θ-α=90^◦ a maksymalna ΔC_pmax=1 w punktach spiętrzenia.

Dla opływu cyrkulacyjnego mamy superpozycję przepływu równoległego, dipola o momencie M i wiru płaskiego o cyrkulacji Г:

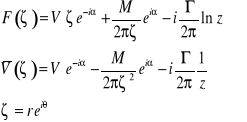
(29)

Prędkość styczna jest równa:

(30)

Żądając, aby punkt spiętrzenia znajdował się w ostrzu (na walcu odpowiadają mu współrzędne (R, -ε) i podstawiając ε do (30) dostajemy wartość cyrkulacji równą:

(31)

Stąd prędkość styczna jest równa:

(32)

Przykładowy rozkład modułu prędkości bezwymiarowej ilustruje rys. 11

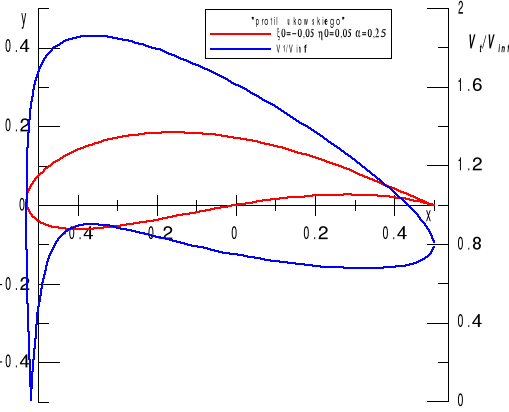
Rys. 11. Rozkład prędkości stycznej na profilu Żukowskiego z Rys. 7.

Obliczenia dla kąta natarcia α=5 stopni.

2.2. Siła nośna na profilu

Uwzględniając wzór Żukowskiego na siłę nośną, dla jednostkowej szerokości walca:

(33)

Oraz empiryczną zależność na siłę nośną, napisaną dla jednostkowej rozpiętości płata:

(35)

Otrzymujemy wzór na współczynnik siły nośnej:

(36)

Dla profili cienkich R≈a i wówczas c≈4R, vide: (12)

Stąd:

(37)

Kąt ostrza ε pełni tu rolę kąta zerowej siły nośnej:

(38)

Dla małych kątów (-/+12 stopni) słuszne jest przybliżenie:

(39)

wykazujące dobrą zgodność z danymi doświadczalnymi.

Uwaga:

Skorygowane zostały błędy we wzorach (21 i 22) z poprzedniej wersji wykładu.

27 I 2011 r.

---