Wykład 21

Siła Ampère'a

Oddziaływanie pola magnetycznego na przewodniki z prądem zostało wykryte przez H.Ch.Oersteda i A.M.Ampère'a. Znajdziemy wzór na siłę, z którą pole magnetyczne oddziałuje na przewodnik z prądem.

Element przewodnika z prądem o objętości
posiada ładunek elektryczny
, gdzie
- koncentracja elektronów przewodnictwa w jednostce objętości;
- ładunek elektronu. A zatem magnetyczna składowa siły Lorentza
, działającej na element
przewodnika wynosi

, (XXI.1)

gdzie
- prędkość średnia uporządkowanego ruchu elektronów.

Ponieważ wektor gęstości prądu
, ze wzoru (XXI.1) znajdujemy

. (XXI.2)

W przypadku przewodnika prostoliniowego:
, gdzie
- długość odcinka przewodnika, a
- pole powierzchni przekroju przewodnika. Wprowadzając wektor
, ze wzoru (XXI.2) otrzymujemy

. (XXI.3)

Tu uwzględniliśmy, że
jest natężeniem prądu płynącego przez przewodnik.

Równania (XXI.2) i (XXI.3) umożliwiają określanie siły działającej na przewodnik z prądem, znajdujący się w polu magnetycznym. Siłę
, określoną wzorami (XXI.2) i (XXI.3), nazywamy siła Ampère'a.

Moment sił działających na zamknięty obwód z prądem. Magnetyczny moment dipolowy

Rozważmy zamknięty obwód z prądem
w postaci prostokątnej ramki. Wybierzmy jednostkowy wektor
prostopadły do płaszczyzny ramki. Kierunek wektora
jest związany z kierunkiem prądu w ramce "prawem korkociągu". Umieścimy prostokątną ramkę ABCD w jednorodnym polu magnetycznym tak aby boki AB i CD były prostopadłe do kierunku wektora indukcji pola magnetycznego
. Oznaczmy kąt między wektorem
i wektorem
jako
. Oznaczmy przez
siły Ampère'a działające na strony ramki. Znajdziemy wypadkowy moment tych sił względem centrum ramki (punkt
).

Siły i mają wartości liczbowe równe . i skierowane są wzdłuż osi pionowej ramki. Dzięki temu momenty sił i względem punktu są równe zeru:

,

ponieważ (
). Siły
i
wywołują deformację ramki w kierunku osi pionowej.

Siły i znajdują się w płaszczyźnie, w której znajdują się wektory i . Wektory i są prostopadłe do wektora , a zatem kąt miedzy wektorami i będzie równy kątowi między wektorami i i jest równy .

Wartość liczbowa sił
i
wynosi

,

a zatem moment pary sił
i
względem punktu
jest równy

,

lub

, (XXI.4)

gdzie
oznacza powierzchnię ramki.

Iloczyn prądu
płynącego w obwodzie i pola
powierzchni tego obwodu nazywa się momentem magnetycznym
obwodu z prądem

. (XXI.5)

Moment magnetyczny jest wielkością wektorową. Wektor
jest prostopadły do płaszczyzny obwodu z prądem a kierunek
i kierunek prądu związane między sobą regułą prawoskrętnego śruba:

. (XXI.6)

Łatwo sprawdzić, że
, a kierunek wektora
pokrywa się z kierunkiem wektora
. A zatem w postaci wektorowej wzór (XXI.4) możemy zapisać w postaci

. (XXI.7)

Można pokazać, że wzór (XXI.7) jest prawdziwy dla dowolnego płaskiego obwodu z prądem niezależnie od jego kształtu.

Ze wzoru (XXI.7) wynika, że istnieją dwa położenia ramki
i
dla których moment sił Ampère'a równa się zeru. We wszystkich pozostałych przypadkach niezerowy moment sił ramki powoduję, że ramka będzie

Как следует из формулы (4.3.8) для момента амперовых сил, существует два положения ၡ = 0 и ၡ = ၰ, в которых этот момент обращается в нуль. В остальных случаях (см. рис.4.3.2) вращающий момент, действующий на контур с током, стремится развернуть контур так, чтобы направление магнитного момента контура совпало с направлением магнитной индукции внешнего поля, т.е. к состоянию ၡ = 0. Поэтому при ၡ = 0 контур оказывается в устойчивом равновесии, а при ၡ = ၰ - в неустойчивом.

Praca wykonana przy przemieszczeniu przewodnika z prądem w polu magnetycznym

Praca
wykonana siłą Ampère'a przy przemieszczaniu o
elementu
obwodu z prądem
w polu magnetycznym
wynosi

. (XXI.8)

Tu skorzystaliśmy z następującego wzoru na iloczyn mieszany
=
=
.

Iloczyn wektorowy
jest pole powierzchni, opisanej przez element
przy jego przemieszczeniu o
. A zatem

. (XXI.9)

Po podstawieniu (XXI.9) do (XXI.8) otrzymujemy . (XXI.10) Ponieważ równa się strumieniowi magnetycznemu przez powierzchnie , wzór (XXI.10) można przepisać w postaci

. (XXI.11)

Zakładając, że natężenie prądu jest stałe i całkując wzór (XX.I.11) uzyskujemy

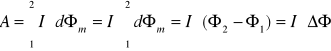
. (XXI.12)

Praca wykonywana przez siły Ampère'a przy przemieszczeniu w polu magnetycznym elementu obwodu zamkniętego albo całego obwodu w którym płynie prąd stały, równa się iloczynowi natężeniu prądu i zmiany strumienia magnetycznego przechodzącego przez powierzchnie ograniczoną obwodem. Praca przemieszczania przewodników z prądem w polu magnetycznym wykonywana jest kosztem energii źródeł siły elektromotorycznej (ogniw galwanicznych, akumulatorów itp.); źródła te wytwarzają w nich prąd elektryczny.

Pole magnetyczne w materii. Namagnesowanie. Wektor natężenia pola magnetycznego

W nauce o magnetyzmie ważną rolę odegrała hipoteza Ampère, według której właściwości magnetyczne materii jest uwarunkowane momentami magnetycznymi cząstek, czyli zamkniętymi prądami płynącymi w cząstkach materii - atomach, molekułach.

W zewnętrznym polu magnetycznym
wszystkie ciała uzyskują makroskopowy moment magnetyczny. Mówimy, że ciało zostało namagnesowane. Indukowany makroskopowy moment magnetyczny ciała wytwarza we wnętrzu ciała dodatkowe pole magnetyczne
, które razem z polem zewnętrznym
tworzą w substancji wypadkowe pole magnetyczne
:

. (XXI.13)

Źródłem pola
są prądy zewnętrzne, czyli prądy, które płyną w przewodnikach umieszczonych na zewnątrz ciała. Natomiast źródłem pola dodatkowego
są prądy molekularne, które tworzą makroskopowy moment magnetyczny substancji. A zatem prawo Ampère'a albo prawo przepływu prądu (patrz wzór (XX.22)) dla cyrkulacji pola magnetycznego we wnętrzu ciała przyjmuje postać

. (XXI.14)

Tu przez
jest sumą algebraiczną prądów przewodzenia (prądów swobodnych), a
jest sumą algebraiczną prądów molekularnych (prądów związanych), które obejmuje obwód
.

W celu scharakteryzowania stanu namagnesowania ciała wprowadzamy wielkość fizyczną, zwaną namagnesowaniem
:

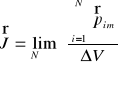
, (XXI.15)

gdzie
oznacza liczbę cząstek, zawartych w objętości
, a
- moment magnetyczny
tej cząstki z objętości
.

Znajdziemy związek pomiędzy
i namagnesowaniem
. Załóżmy, że momenty magnetyczne prądów molekularnych zorientowany jednakowo i niech
jest kątem miedzy wektorem
zamkniętego obwodu
i wektorem
. Objętość walca pokazanego na rysunku jest równa

. Jeżeli oznaczmy, przez koncentrację momentów magnetycznych w jednostce objętości, a przez - prąd molekularny płynący w cząstce, wtedy dla wypadkowego prądu molekularnego owijającego element obwodu wynosi

. (XXI.16)

Tu uwzględniliśmy, że
.

Całkując wzór (XXI.16) wzdłuż zamkniętego obwodu
otrzymujemy sumę algebraiczną prądów molekularnych (prądów związanych), które obejmuje obwód
:

. (XXI.17)

Można wykazać, że wzór (XXI.17) jest słuszny również w przypadku chaotycznej orientacji molekularnych momentów magnetycznych. A zatem, cyrkulacja wektora namagnesowania
wzdłuż dowolnego zamkniętego obwodu
równa się sumie algebraicznej prądów molekularnych, które obejmują ten obwód.

Zgodnie z prawem Ampère'a (XXI.14)

. (XXI.18)

A zatem, biorąc pod uwagę (XXI.19), dla pola magnetycznego
, które wytwarzają prądy molekularne uzyskujemy

. (XXI.19)

Biorąc pod uwagę wzór (XXI.17), ze wzoru (XXI.14) otrzymujemy

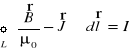
. (XXI.20)

Tu
- przenikalność magnetyczna próżni.

Wektor

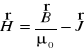
(XXI.21)

nosi nazwę wektora natężenia pola magnetycznego.

Zgodnie z (XXI.20) cyrkulacja wektora natężenia pola magnetycznego wzdłuż dowolnego obwodu zamkniętego
równa się sumie algebraicznej prądów przewodzenia, które obejmuje ten obwód:

. (XXI.22)

Korzystając z twierdzenia Stokes (XX.35) i wzoru (XXI.22)

otrzymujmy

. (XXI.23)

Z doświadczeń wynika, że dla wielu substancji namagnesowanie jest wprost proporcjonalne do
(
). Wtedy zgodnie z (XXI.21) namagnesowanie jest wprost proporcjonalne do wektora
:

, (XXI.24)

gdzie współczynnik
nazywa się podatnością magnetycznej substancji.

Uwzględniając (XXI.24) ze wzoru (XXI.21) znajdujemy

, (XXI.25)

gdzie wielkość

(XXI.26)

nazywa się przenikalnością magnetyczną danej substancji.

Biorąc pod uwagę wzór (XXI.13) (
) oraz wzór (XXI.19) (
), ze wzoru (XXI.25) znajdujemy

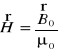
. (XXI.27)

Podstawiając wyrażenie (XXI.27) do wzoru (XXI.25) otrzymujemy

. (XXI.28)

Ze wzoru (XXI.22) widzimy, że natężenie pola magnetycznego jest podobne do wektora indukcji elektrycznej
. Wektor indukcji elektrycznej określają tylko ładunki swobodne. Wektor
określają tylko prądy swobodne. Wektor
ma taką samą wartość w jednorodnym polu elektrycznym na zewnątrz oraz wewnątrz dielektryka. Wektor
tak same ma taką sama wartość w jednorodnym polu magnetycznym na zewnątrz oraz wewnątrz ciała (patrz wzór (XXI.27)).

Z doświadczeń wynika, że dla większości ciał przenikalność magnetyczne
nie zależy od
i nie znacznie różni się od jedynki. Takie ciała zostały podzielone na paramagnetyki i diamagnetyki.

Dla paramagnetyków
(
), a zatem zgodnie z (XXI.28) pole magnetyczne wewnątrz ciała będzie większe od pola zewnętrznego (
).

Diamagnetyki ( , ) są to substancje, które magnetyzują się w kierunku przeciwnym do kierunku pola magnetycznego , a zatem pole magnetyczne wewnątrz ciała

będzie mniejsze od pola zewnętrznego (
). Istnieje też liczna grupa ciał, które nawet w zerowym polu magnetycznym posiadają niezerowe namagnesowanie. To są substancje uporządkowane magnetycznie, dla których
.

Warunki graniczne dla wektorów
i
na powierzchni styku dwóch ciał

Załóżmy, że na granice styku dwóch ciał przez powierzchnie ograniczoną konturem
nie płyną żadne prądy swobodne. Zachowanie wektora
i
na powierzchni styku dwóch ciał znajdziemy korzystając z twierdzenia (XXI.22) o cyrkulacji wektora
i prawa Gaussa dla wektora
. W przypadku, gdy
, twierdzenie o cyrkulacji wektora
ma postać

. (XXI.29) Dla dość małego ( ), ze wzoru (XXI.29) otrzymujemy . Skąd mamy

. (XXI.30)

Biorąc pod uwagę, że
ze wzoru (XXI.30) uzyskujemy

. (XXI.31)

Z twierdzenia Gaussa dla wektora indukcji pola magnetycznego
(
) dla dość małego
(
) znajdujemy

. Skąd wynika, że . (XXI.32) Biorąc pod uwagę wzór (XXI.25) ze wzoru (XXI.32) mamy . (XXI.33)

Na zakończenie wypiszemy różniczkowe równania dla stałego (
) pola magnetycznego i pola elektrostatycznego (
) w materii:

,
; (XXI.34)

,
. (XXI.35)

Podkreślimy, że podstawowymi charakterystykami pola elektrycznego i magnetycznego są wektor natężenia pola elektrycznego
i wektor indukcji magnetycznej
. Wektor indukcji elektrycznej
i wektor natężenia pola magnetycznego
są pomocnicze wektory, które wprowadzamy w celu uproszczenia opisu pola elektromagnetycznego w różnych ośrodkach.

Przypomnimy, że między podstawowymi wektorami
i wektorami pomocniczymi
istnieją, w przypadku izotropowej substancji, związki

,
. (XXI.36)

W przypadku ośrodków anizotropowych zamiast wzorów (XXI.36) mamy

,
. (XXI.37)

Indukcja elektromagnetyczna. Prawo indukcji Faradaya i reguła Lenza

Dotychczas rozważaliśmy statyczne pole elektryczne i magnetyczne. Dla tych pól, jak widać ze wzorów (XXI.34) i (XXI.35), pole elektryczne i pole magnetyczne istnieją niezależnie od siebie. Okazało się jednak, że w przypadku pól zmiennych w czasie pole magnetyczne i pole elektryczne nie są niezależne od siebie i tworzą jedyne pole elektromagnetyczne.

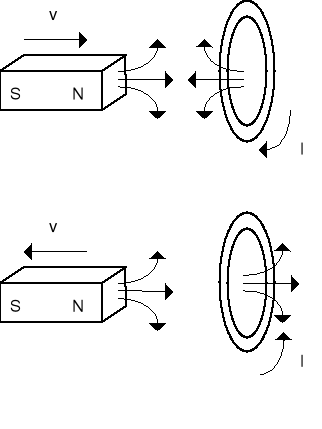
Po raz pierwszy związek między elektrycznymi i magnetycznymi polami wykrył w 1832 roku Faraday. Zjawisko, które odkrył Faraday nosi nazwę indukcji elektromagnetycznej i polega ono na powstawaniu prądów elektrycznych w zamkniętym obwodzie podczas przemieszczania się względem siebie źródła pola magnetycznego i tego zamkniętego obwodu. Mówimy, że w obwodzie jest indukowana siła elektromotoryczna (SEM indukcji), która wywołuje przepływ prądu indukcyjnego.

Prawo indukcji Faradaya stosuje się do trzech różnych sytuacji fizycznych:

• Nieruchoma pętla, względem której porusza się źródło pola magnetycznego (mamy tzw. elektryczną SEM).

• Przewód w kształcie pętli porusza się w obszarze pola magnetycznego (magnetyczna SEM).

• Nieruchoma pętla i nieruchome źródło pola magnetycznego, lecz zmienia się prąd, który jest źródłem pola magnetycznego (także elektryczna SEM).

Na podstawie obserwacji Faraday doszedł do wniosku, że indukowana w obwodzie siła elektromotoryczna
jest wziętej ze znakiem ujemnym szybkość, z jaką zmienia się strumień
przechodzący przez ten obwód:

. (XXI.38)

Znak minus w prawie Faradaya wyraża tak zwaną regułę Lenza: prąd indukowany w obwodzie ma zawsze taki kierunek, że wywołane przez niego pole magnetyczne przeciwdziała zmianom, które wywołują jego powstanie. Kierunek prądu indukowanego w pętli (rysunek) zależy od tego czy strumień rośnie czy maleje (zbliżamy czy oddalamy magnes). Jeżeli mamy obwód złożony z zwojów to

. (XXI.39)

W układzie SI jako jednostkę strumienia magnetycznego przyjmuje się 1 weber (Wb): 1 Wb = 1 T ·1 m².

69

---