Granica funkcji

1) Obliczyć granice jednostronne funkcji w podanym punkcie :

a)
,
; b)
,
; c)
,
d)
,
; e)
,
;

2) Obliczyć granice :

1)
; 2)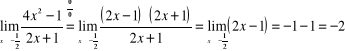
;

UWAGA . Gdy po wstawieniu liczby
do licznika i mianownika otrzymujemy symbol nieoznaczony
i licznik i mianownik są wielomianami , rozkładamy licznik i mianownik na czynniki .

3)

; 4)
;

UWAGA . Przypominamy wzory : (1)

(1a)
;

(2)
; (3)
; (4)
(5)
; (6)
; (7)
.

5)
;

6)
;

7)
;

8)
= { korzystamy ze wzoru (1a) } =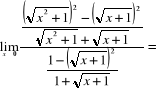

=
;

9)
;

10)
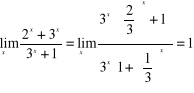
, bo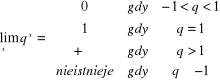
;

11)
{ dzielimy licznik i mianownik przez
} =
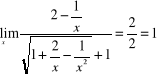
{ bo
, gdy
} ;

12)
;

13)
;

UWAGA . Należy znać granice ! : (1)
; (2)
; (3)
(4)
; (5)
=
; (6)
=
.

14)
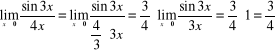
{ bo we wzorze (1) przyjmujemy
} ;

15)
;

16)
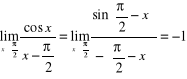
{ zauważmy, że gdy
, to
; przyjmując więc
we wzorze (1) otrzymujemy podaną granicę } ;

17)
;

18)

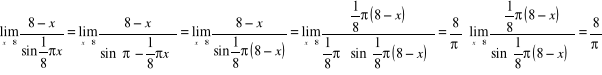
{ wykorzystaliśmy wzór redukcyjny :
}

19)

=
;

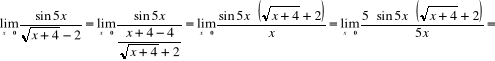
20)
=
;

21)
= { korzystamy ze wzoru :
} =

=
;

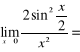
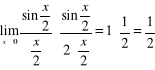
22)
;

23)
;

24)
;

25)
;

26)
;

27)
- korzystamy tu z twierdzenia :

Jeżeli
, to
.

28)
;

29)
;

30)
;

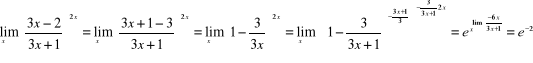
31)
, bo z twierdzenia o trzech granicach mamy :
i
;

32)
.

1

---