Ciągłość funkcji

Funkcja
jest ciągła w punkcie
, gdy ;

1)
;

2) istnieje
;

3)
.

1. Zbadać ciągłość funkcji :

a)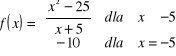
.

Dziedziną funkcji jest zbiór
. Dla
funkcję można zapisać wzorem :
, która jest ciągła w całej dziedzinie . Zatem zbadamy ciągłość funkcji
w punkcie
:

=
co oznacza , że funkcja jest ciągła w punkcie
, zatem i w zbiorze
.

b)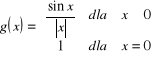
.

Mamy :
i
. Zbadamy teraz istnienie granicy w punkcie
. Ponieważ

, więc
,
. Granice jednostronne są różne , więc funkcja nie ma granicy w punkcie
, a tym samym podana funkcja nie jest ciągła w punkcie
.

2. Określić funkcję tak , aby była ciągła w punkcie
:

a)
.

i
=
.

Punkt
, więc funkcja nie jest ciągła w tym punkcie . Ale
. Zatem funkcja określona następująco :

=
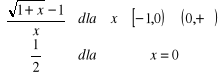
jest ciągła w punkcie
.

b)
. Dziedziną funkcji jest zbiór
. Funkcja ta nie jest ciągła w punkcie
, bo nie jest ona określona w tym punkcie . Sprawdzimy istnienie granicy . Ponieważ

i
, to
. Zatem funkcja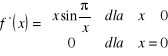
jest ciągła w punkcie
.

c)
.
=
= R\
.

Funkcja nie jest ciągła w punktach
dla
. Zauważmy , że
. (błąd ! - granica jest liczona w punktach
- poprawić - wstawić
) !!!

Funkcja określona wzorem :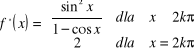
jest ciągła w
.

Dla
z powyższego otrzymujemy wniosek : funkcja
jest ciągła w punkcie
.

3. Dla jakiej wartości parametru
funkcja jest ciągła w punkcie
:

a)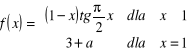
,
.

Aby funkcja była ciągła w punkcie
musi spełniać warunek :
. Mamy :

,

.

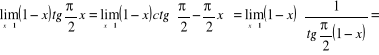
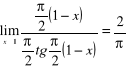
Zatem dla


funkcja
jest ciągła .

b)
,
.

Mamy :

,
. Stąd




lub

Zatem dla
i dla
podana funkcja jest ciągła w punkcie
.

4 . Czy następujące funkcje są ciągłe w przedziale
?

a)
.

Funkcja
jest sklejeniem funkcji kwadratowej i liniowej , które są ciągłe jako funkcje elementarne . Zatem funkcja
może być nieciągła w punkcie
( w punkcie sklejenia ) . Mamy :
. Zbadamy istnienie granicy w tym punkcie . Obliczamy granice jednostronne ponieważ po obu stronach punktu
funkcja określona jest różnymi wzorami .

,
. Z równości granic jednostronnych wynika , że funkcja ma granicę i
. Widać , że
co oznacza , że funkcja jest ciągła w przedziale
.

b)
.

Badamy ciągłość w punkcie
( wyjaśnienie jak wyżej ) .

.
,
. Granice jednostronne są różne więc funkcja nie ma granicy w punkcie
, tym samym jest nieciągła w tym punkcie , co dalej oznacza , że jest nieciągła w przedziale
.

5 . Wyznaczyć punkty nieciągłości danej funkcji i określić ich rodzaj :

a)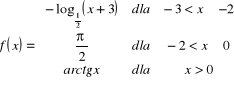
.

Funkcja określona jest w przedziale
.

` Badamy ciągłość tej funkcji w punktach , w których zmienia się wzór (punkty sklejenia ) . Punktami tymi są
i
.

W punkcie
mamy :
. Obliczamy granice jednostronne :

;
. Granice te są różne co oznacza , że funkcja jest nieciągła w punkcie
( bo nie istnieje granica - warunkiem istnienia granicy jest istnienie i równość granic jednostronnych ) . Ponieważ funkcja
jest określona w punkcie
i granice jednostronne są różne ale skończone , to funkcja ma w tym punkcie nieciągłość I-szego rodzaju - w punkcie
jest skok funkcji .

Sprawdzamy teraz warunki ciągłości funkcji w punkcie
. Mamy :
.

,
. Ponieważ granice te są różne więc funkcja nie ma w tym punkcie granicy i , zatem , nie jest ciągła . Jest to nieciągłość pierwszego rodzaju typu skok (uzasadnienie jak wyżej ) .

b)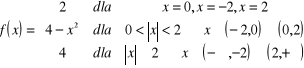
.

Sprawdzamy ciągłość funkcji w punktach :
,
,
.

.

;


. Ponieważ wartość funkcji w punkcie
i granica w tym punkcie są różne to funkcja jest nieciągła . Jest to nieciągłość pierwszego rodzaju .

.

;
,
.Granice te są różne więc granica funkcji nie istnieje i stąd funkcja w tym punkcie jest nieciągła . Granice jednostronne są skończone i różne , jest to więc nieciągłość pierwszego rodzaju typu skok .

.

;
,
. Funkcja jest nieciągła w punkcie
, bo nie ma w tym punkcie granicy . Jest to także nieciągłość pierwszego rodzaju .

6 . Jeżeli funkcja
określona w przedziale domkniętym
jest w nim ciągła i
, to istnieje punkt
taki , że
.

,
.

Zbadamy ciągłość tej funkcji w punkcie
, w którym funkcja zmienia wzór . Mamy
i
,
. Ponieważ granice jednostronne są różne więc nie istnieje granica funkcji w tym punkcie . Oznacza to , że funkcja jest nieciągła w punkcie
i tym samym jest nieciągła w przedziale
. Stąd wniosek : nie istnieje punkt
taki , w którym
.

7 . Czy funkcja
przybiera wartość
wewnątrz przedziału
?

Podana funkcja jest ciągła w przedziale
jako suma funkcji elementarnych ( które są ciągłe ) .

Korzystamy tu z następującej własności funkcji ciągłych :

Jeżeli funkcja określona w przedziale
jest w nim ciągła i przyjmuje w punktach
dwie rożne wartości
,
, to w przedziale

przyjmuje wszystkie wartości pośrednie , tj. dla każdego
zawartego między
i
istnieje takie
, że
.

Zauważmy , że
, liczba
leży między liczbami 1 i 5 , więc istnieje taka liczba
, że
, tzn.
.

3

---