Pojęcie funkcji pierwotnej

 

Definicja:

Niech dana będzie funkcja f: DႮR. Funkcją pierwotną funkcji f nazywamy funkcję F: DႮR taką, że:

კ F ` ( x ) = f ( x )

X ჎ D

Twierdzenie:

Jeżeli funkcje F: DႮR i G: DႮR są funkcjami pierwotnymi funkcji f: DႮR to istnieje takie C჎R że zachodzi:

G(x) = F(x) + C

Twierdzenie:

Funkcje pierwotne funkcji f(x) różnią się co najwyżej o stałą

Zapis: G(x) = F(x) + C oznacza rodzinę funkcji f.

CAŁKOWANIE PRZEZ CZĘŚCI

 

Twierdzenie: ြ o całkowaniu przez części ှ

Jeżeli funkcje f i g mają w przedziale D ciągłe pochodne f' i g' to zachodzi wzór:

CAŁKOWANIE PRZEZ PODSTAWIENIE

 

Metoda całkowania przez podstawienie, zwana jest także metodą całkowania przez zmianę zmiennej.

Twierdzenie:ြ pierwsze o całkowaniu przez podstawienie t = h(x) ှ

Jeżeli:

1. Funkcja h(x) jest różniczkowalna w przedziale D i przekształca go na przedział T

2. Funkcja g(t) ma w przedziale T funkcję pierwotną G(t)

3. f(x) = g[h(x)] w przedziale D

to:

CAŁKA OZNACZONA

1.

Definicja:

Niech f będzie funkcją ciągłą na przedziale ြa,bှ i F jej funkcją pierwotną.

Liczbę F(b) - F(a) nazywamy całką oznaczoną funkcji f na przedziale ြa,bှ i

oznaczamy:

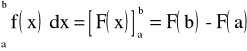
Liczby a i b nazywamy odpowiednio dolną i górną granicą całkowania.

Twierdzenie:

1.

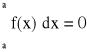
2.

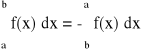
3. Jeżeli aြ cြ b, to: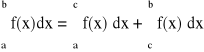

Geometryczne zastosowanie całki oznaczonej.

Twierdzenie:

Niech y = f(x) będzie funkcją ciągłą na przedziale ြa,bှ wtedy:

1. 1.      Objętość bryły obrotowej powstałej poprzez obrót obszaru ograniczonego łukiem krzywej

y = f(x), prostymi x = a i x = b oraz osią OX dookoła tej osi wyraża się wzorem:

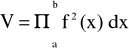
2. 2.      Pole powierzchni bocznej:

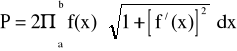
3. 3.      Długość łuku krzywej:

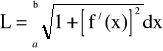
Całka niewłaściwa pierwszego rodzaju.

1. Funkcja podcałkowa f(x) nie jest ograniczona w otoczeniu punktu x = b, wówczas całkę określamy następująco:

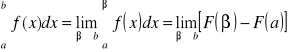
, a < β < b,

jeśli ta granica istnieje.

2. Funkcja podcałkowa f(x) nie jest ograniczona w otoczeniu punktu x = a, wówczas całkę określamy następująco:

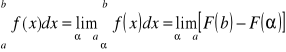
, a < α < b,

jeśli ta granica istnieje.

3. Jeżeli natomiast funkcja podcałkowa f(x) nie jest ograniczona w pewnym otoczeniu punktu x = c, gdzie a < c < b, to całkę określamy następująco:

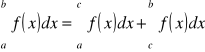
2. Całka niewłaściwa drugiego rodzaju.

Funkcja f(x) jest określona i ciągła w przedziale
, wówczas całkę funkcji f(x) w przedziale
określamy następująco:

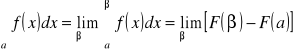
Jeżeli granica po prawej stronie nie istnieje, to mówimy, że całka niewłaściwa nie istnieje.

1. Jeżeli niewłaściwość występuje na lewym końcu przedziału całkowania
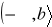
   , to całkę określamy następująco:

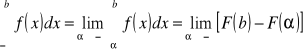
2. Przyjmijmy także określenie:

,

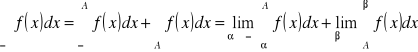
gdzie A jest dowolną liczbą.

Jeżeli istnieją skończone granice określające całki niewłaściwe pierwszego i drugiego rodzaju, to całki te nazywamy zbieżnymi. W przeciwnym razie nazywamy je rozbieżnymi.

Mnożenie macierz przez macierz- mnożenie macierzy nie jest przemienne, ilość kolumn pierwszej musi być równa ilości wierszy drugiej (Schemat Falka)

schemat Falka:

A

B AB

Element cij macierzy C = AB otrzymujemy na przecieciu linii wyznaczonych

przez i-ty wiersz macierzy A i j-ta kolumne macierzy B.

Postać bazowa macierzy (macierz bazowa) dla macierzy A

gdzie Ik jest macierzą jednostkową stopnia k, zaś O1 i O2 są macierzami zerowymi.

Przekształceniami elementarnymi danej macierzy A=[aij]m x n nazywamy następujące działania na wierszach lub kolumnach macierzy: T1 - polega na pomnożeniu wszystkich elementów wybranego wiersza lub kolumny przez liczbę α0, ≠T2 - polega na zamianie miejscami dwóch dowolnie wybranych wierszy lub kolumn, T3 -polega na dodaniu do wszystkich elementów wybranego wiersza lub kolumny odpowiadających im elementów innego wiersza lub kolumny pomnożonych przez liczbę α0.

monotoniczność funkcji - jeżeli w danym przedziale pochodna funkcji poza skończoną liczbą punktów przyjmuje wartości dodatnie, to funkcja w tym przedziale jest rosnąca, z kolei jeżeli w danym przedziale pochodna funkcji poza skończoną liczbą punktów przyjmuje wartości ujemne, to funkcja w tym przedziale jest malejąca, podobnie, jeśli pochodna w przedziale przyjmuje wartości nieujemne, funkcja jest w przedziale niemalejąca, a jeśli niedodatnie - nierosnąca

calka oznaczona

Całkowanie przez części. Jeżeli
są funkcjami zmiennej
mającymi ciągłą pochodną to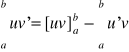
.

Całkowanie przez podstawienie. Jeżeli
jest funkcją ciągłą,
funkcją rosnącą w przedziale
, a
funkcją ciągłą w przedziale
, to zachodzi

---