Politechnika Śląska

Wydział Elektryczny

Kierunek EiT

Ćwiczenie laboratoryjne z fizyki

Pomiar prędkości dźwięku w powietrzu.

Metoda rezonansowa.

Grupa T2 sekcja I

Tomasz Hauser

Paweł Łoskot

Gliwice 15.02.1999r.

1. Wprowadzenie

1.1 Fala akustyczna

Rozchodzenie się dźwięku w powietrzu jest zjawiskiem falowym. Jest to zaburzenie rozchodzące się w ośrodku sprężystym ( powietrzu ), polegające na przenoszeniu energii przez drgające cząstki ośrodka bez zmiany ich średniego położenia. Fala akustyczna jest sprężystą falą podłużną. Równanie tej fali rozchodzącej się wzdłuż osi x, w dwóch punktach odległych od siebie o r ma postać:

y1 = A cos [ 2 ( t/T - x/l) + d ]

y2 = A cos [ 2 ( t/T - (x + r)/l ) + δ ].

Między falą w punkcie 1 i 2 istnieje dodatkowa różnica fazy

δ = 2n r / c

gdzie: c - prędkość propagacji fali.

Zakładając że w punktach 1 i 2 są dwa kolejne węzły otrzymujemy:

 =  (ri i - ri-1) /c.

podstawiając:

δri = ri - ri-1

otrzymujemy:

c = 2 δri.

Analogicznie postępując możemy otrzymać wzór, w którym zmieniana jest częstotliwość - dla tegosamego punktu po zmianie częstotliwości powinniśmy otrzymać ponownie węzeł. Wzór na prędkość propagacji fali ma wtedy postać:

c = 2r δi

Rozchodzenie się fali jest równierz procesem termodynamicznym. Zagęszczenia i rozrzedzenia ośrodka, który jest nośnikiem fali, są adiabatyczne - ze względu na dużą szybkość propagacji fali w powietrzu. Znając cp / cv =  można wzór na propagację fali w powietrzu zapisać w postaci:

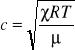
gdzie :

R- uniwersalna stała gazowa,

T- temperatura w kelwinach,

- masa molowa powietrza.

1.2. Fale stojące

W wyniku interferencji dwóch fal, biegnących na przeciw siebie, o równaniach:

y1 = A cos 2 ( t/T - x/l )

y2 = A cos 2 ( t/T + x/l )

otrzymamy falę wypadkową o równaniu :

y = y1 + y2 = 2A cos 2 x/l cos 2 t/T

Analizując powyższe równanie otrzymujemy warunki na istnienie fali stojącej. W przypadku rury Kundta, gdy fala jest ograniczona dwoma ośrodkami gęstszymi warunek ten przyjmuje pstać: l=(2n+1)*l/4, co oznacza, że fala stojąca wytworzy się tylko w rurze o takiej długości, gdy mieści się w niej nieparzysta liczba ćwiartek fal. Analizując równanie fali można również podać warunki na istnienie węzłów i strzałek. Węzły, czyli punkty w których nie występują drgania powstają w miejscach spełniającym warunek : x=(2n+1)*l/4, a strzałki, czyli punkty w których amplituda drgań jest maksymalna, powstają w punktach spełniających warunek: x=n*l/2.

2. Schematy układów

2.1. Metoda rezonansowa

W pierwszej części ćwiczenia dokonywano pomiaru prędkości dźwięku w powietrzu metodą rezonansową. W celu dokonania pomiarów zbudowano układ według schematu przedstawionego poniżej.

Schemat 1.

gdzie:

G- generator, F- częstotliwościomierz,

1-głośnik, 2-rura Kundta,

3-mikrofon, 4-oscyloskop

2.2 Opis przebiegu ćwiczenia

Układ zbudowano jak na schemacie 1. Pomiarów dokonywano w następujący sposób:

1. Ustawiano częstotliwość f0 i szukano takiego położenia mikrofonu by wskaznie na oscyloskopie było maksymalne ( strzałka ).

2. Nie zmieniając położenia mikrofnu szukano dwóch najbliższych wartości częstotliwości odpowiadających rezonansowi akustycznemu.

Ogółem dokonano 5 serii pomiarów według powyżej przedstawionej kolejności.

3. Tabele z wynikami pomiarów

Odległość L [cm]	Częstotliwość [Hz]
	f1	f0	f2
1
2
3
4
5

3.1. Obliczenia i analiza błędów

Do obliczeń przyjęto następujące wartości błędów wynikających z niedokładności odczytu i niedoskonałości mierników:

l = 0.005 [m] - błąd odczytu z przymiaru,

f = 3 [Hz] - błąd częstotliwościomierza,

T = 0.5 [° C] = 273.8 [K]- błąd odczytu z termometru.

Wstawiając do wzorów na prędkość fali w zależności od różnicy faz obliczono prędkości dźwięku ( c ) w powietrzu. Następnie ze wzoru na różniczkę zupełną obliczono błąd ( c )

c = 2 l | f0 -f1 | i c = 2 l | f0 -f2 |

c = | 2 ( f0-f1 ) | | l | + | 2 l | |f | i c = | 2 ( f0-f2 ) | | l | + | 2 l | |f |

Po wstawieniu odpowiednich danych uzyskano następujące wartości prędkości oraz błędy dla odpowiednich prędkości:

 - różnica faz	| f0 - f1 |					| f0 - f2 |
nr	1	2	3	4	5	1	2	3	4	5
c - prędkość dzwięku [m/s]
c - błąd obliczeń [m/s]

Z obliceń w dalszej części ćwiczenia wyłączono pomiary 1 i 2 dla różnicy faz | f0 - f1 |, gdyż wyniki wskazują na błąd gruby spowodowany najprawdopodobniej złym doborem częstotliwości rezonansowej a raczej jej nie znaleźieniem (wysoka prosta lecz nie rezonansowa).

Stosując wzór na średnią ważoną otrzymano wartość prędkości dźwięku w powietrzu oraz błąd średniej ważonej:

c=341.9 [m/s] ,

c=14.3 [m/s]

4. Podsumowanie

Otrzymana prędkość dźwięku w powietrzu:

c=341.9 ± 14.3 [m/s]

Za pomocą wyznaczonej prędkości obliczono wykładnik adiabaty:

 ± 1

Wartość tablicowa  δla powietrza wynosi t=1.40. Dzięki znajomości  można porównać wyznaczoną prędkość z wartością tablicową prędkości propagacji dźwięku w powietrzu (w tmperaturze 273 K). Prędkość c0 wyznaczono korzystając ze wzoru:

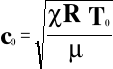
i wyniosła ona:

c=328.1 [m/s]

Błąd uzyskanego wyniku liczono ze wzoru:

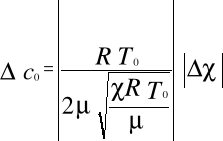
Wyniósł on odpowiednio:

c=28.0 [m/s]

Wartość tablicowa c0 wynosi c0=331 [m/s]. Porównanie ze sobą prędkości otrzymanych z pomiaru z wartością tablicową prowadzi do wniosku, że metoda przesunięcia fazowego jest dookładniejsza niż metoda rezonansowa ponieważ otrzymany wynik jest obarczony mniejszym błędem, a wartość prędkości jest dokładniejsza. Otrzymano za jej pomocą wartość: c=330.5±7.6 [m/s]. Odchyłka od wartości tablicowej liczonej wg wzoru:

σ= (c0 / c -1) *100%

wynosi σ=0.2 %. Używając metody rezonansowej otrzymano: c=328.1±28.0 [m/s]. W tym przypadku σ=0.9%.

Warto zauważyć że metoda przesunięcia fazowego powinna być metodą bardziej dokładną poniewarz opiera sie na różnicy odległości i wszelkie błędy wyskalowania miarki długości są mniej prawdopodobne. W metodzie tej łatwiej też jest ustawić przyżądy w odpowiednich pozycjach - nie nakładanie się fal jest łatwe do zauwarzenia w przeciwieństwie do znaleźienia częstotliwości rezonansowej.

4

---