TRANSPORT JONÓW PRZEZ NANO-KANAŁY W BŁONACH KOMÓRKOWYCH

ION TRANSPORT THROUGH CELLULAR NANOCHANNELS

Jan Gomułkiewicz¹, Jacek Miękisz² i Stanisław Miękisz³

1- Instytut Fizyki Politechniki Wrocławskiej; 2- Instytut Matematyki Stosowanej i Mechaniki Uniwersytetu Warszawskiego; 3- Katedra Biofizyki Akademii Medycznej we Wrocławiu

Streszczenie: W pracy przedstawiono dyskusję teoretycznego opisu transportu jonów w kanałach błon komórkowych. Uzyskane w ostatnich latach dane doświadczalne o budowie kanałów jonowych wykazują, że ich poprzeczne rozmiary są porównywalne z rozmiarami jonów, oraz że równocześnie mogą w nich znajdować się 2-3 jony. Teoretyczny opis transportu jonów w takich kanałach musi wobec tego uwzględniać oddziaływania między jonami oraz niekulombowskie oddziaływanie jonów z białkiem kanałowym. Warunku tego nie spełniają teorie kontynualne oparte o równania Poissona-Nernsta-Plancka, które w związku z tym mogą być traktowane tylko jako grube przybliżenia. Bardziej realistyczne opisy teoretyczne oparte są o dynamikę Brownowską lub dynamikę molekularną. Są to bowiem teorie mikroskopowe. Dostępne w literaturze publikacje nie uwzględniają w zadawalającym zakresie dynamiki cząsteczek białka kanałowego.

Słowa kluczowe: kanały jonowe, transport jonów

Summary: We discuss various models of ion transport through cellular nanochannels. Recent experimental data shows that sizes of ion channels are compared to those of ions and that only few ions may be simultaneously in any single channel. Theoretical description of ion transport in such channels should therefore take into account interactions between ions and between ions and channel proteins. This is not satisfied by macroscopic continuum models based on Poisson-Nernst-Planck equations. More realistic descriptions of ion transport are offered by microscopic Brownian and molecular dynamics. One should also take into account a dynamical character of the channel structure . This is not yet addressed in the literature.

Key words: ion channels, ion transport

1. WPROWADZENIE

Żywa komórka jest układem otwartym. Warunkiem życia jest bowiem ciągła wymiana energii i substancji między komórką a jej otoczeniem. Błony komórkowe, które zapewniają autonomię otoczonych przez nie przedziałów, muszą być wyposażone w mechanizmy selektywnego transportu substancji potrzebnych dla życia komórek. W szczególności bardzo ważnym z punktu widzenia biologii komórki jest transport jonów przez błonę komórkową. Własności transportowe błon muszą zapewnić wewnętrzny skład jonowy komórek różny od składu jonowego ich otoczenia.

Błony komórkowe, z uwagi na ich strukturę i skład chemiczny (dwuwarstwa lipidowa z zanurzonymi w niej cząsteczkami białek integralnych), charakteryzują się bardzo niską średnią względną przenikalnością elektryczną (około 2) w porównaniu do względnej przenikalności elektrycznej wodnych roztworów elektrolitów w ich otoczeniu (około 80). Odpowiadająca tym wartościom względnej przenikalności elektrycznej energia Borna (energia potrzebna do przeniesienia jonu z wodnego roztworu elektrolitu do hydrofobowego wnętrza błony) wynosi około 300 kJ/mol. Tak dużej wartości energii Borna odpowiadać musi bardzo mała przepuszczalność hydrofobowego wnętrza błony dla jonów (w szczególności dla jonów ważnych w elektrofizjologii komórki, takich jak Na⁺, K⁺, Ca⁺⁺ i Cl^-), mniejsza o kilka rzędów wielkości od obserwowanej dla błon komórkowych. W procesach ewolucyjnych ukształtowały się w błonach komórkowych struktury i mechanizmy obniżające lokalnie barierę energetyczną dla przenikających przez nie jonów. Struktury te są utworzone z cząsteczek białek integralnych, których reszty hydrofobowe oddziałują z dwuwarstwą lipidową (matrycą lipidową błony), a reszty polarne (hydrofilne) tworzą: a) względnie szerokie nieselektywne uwodnione pory przenikające przez całą grubość błony, b) specyficzne dla danego rodzaju jonów kanały, często wyposażone w specjalne elementy strukturalne tworzące bramki czułe na pole elektryczne lub ligandy chemiczne czy naprężenia mechaniczne, c) centra wiążące jony (po jednej lub obu stronach błony), zwane nośnikami lub transporterami, które oddziałując z jonami i podlegając zmianom strukturalnym przenoszą jony na drugą stronę błony gdzie następuje dysocjacja kompleksu nośnik-jon. Transport nośnikowy może zachodzić na koszt energii dostarczanej przez reakcje metaboliczne (głównie jest to hydroliza ATP) i mówimy wtedy o transporcie aktywnym (np. pompy jonowe) lub na koszt energii wewnętrznej układu.

Wszystkie wymienione wyżej mechanizmy transportu są istotne dla homeostazy komórkowej, a więc dla zabezpieczenia składu wnętrza komórki, objętości komórki czy też elektrycznego napięcia na błonie (w elektrofizjologii i biofizyce przyjęto to napięcie nazywać potencjałem błonowym). Są one też (w różnym stopniu) istotne dla stanów pobudzenia komórki. Szczególną role w tym ostatnim przypadku odgrywają kanały jonowe. Badania w tym zakresie są bardzo szeroko prowadzone w licznych ośrodkach naukowych, gdzie zebrano bardzo bogaty zbiór danych doświadczalnych i opracowano mniej lub bardziej zaawansowane teorie opisujące transport jonów w kanałach jonowych. Mimo to wiedza z tego zakresu ciągle nie wystarcza by wyjaśnić mechanizm transportu i podać pełny jego opis.

2. KANAŁY JONOWE

Na przełomie lat czterdziestych i pięćdziesiątych, Hodgkin i Huxley we współpracy z Katzem [29,30,31,33,48], opracowując swoją fenomenologiczną teorię impulsu nerwowego, wysunęli hipotezę, że transport jonów sodu i potasu w pobudliwych błonach biologicznych zachodzi przez selektywne centra, różne dla jonów sodowych i potasowych. Centra te poza wysoką selektywnością miały również wykazywać zależność ich przewodnictwa od napięcia elektrycznego na błonie. Wprawdzie nigdzie w pracach tych nie nazwano tego rodzaju centrów kanałami jonowymi, to jednak na tej podstawie powstaje hipoteza, że jony przenikają w błonach pobudliwych przez utworzone z białek kanały jonowe. Hipoteza ta zyskała powszechną akceptację. O własnościach tych kanałów, jak również o mechanizmach transportu jonów przez te kanały wnioskowano z wyników pomiarów makroskopowych. Szczególnie owocną była metoda voltage-clamp, która polega na rejestracji prądów elektrycznych przez określoną makroskopową powierzchnię błony przy ustalonej wartości potencjału błonowego (napięcia na błonie). Układ do pomiarów takich prądów (w aksonach) schematycznie przedstawia rycina 1.

RYCINA 1. Schemat układu do pomiaru prądów jonowych w aksonach metodą voltage-clamp.

Rejestrowany prąd płynący przez błonę jest sumą prądów jonowych i prądu pojemnościowego (prądu ładowania elektrycznej pojemności błony). Ten ostatni zanika ze stałą czasową określoną przez pojemność elektryczną błony i oporność elektryczną obwodu pomiarowego. Dla całkowitego prądu, J_m, (prądu rejestrowanego przez układ pomiarowy) możemy napisać zależność,

, (1)

gdzie J_c jest prądem pojemnościowym, a J_i prądami przenoszonymi przez poszczególne rodzaje jonów (głównie prądu sodowego i potasowego, ale również prądu chlorkowego stanowiącego główny składnik prądu upływu, dla którego przewodnictwo elektryczne błony jest niezależne od potencjału błonowego). Stosując toksyny blokujące specyficznie transport konkretnych jonów, można wydzielić z prądu całkowitego prąd przenoszony przez te jony. Ilustruje to rycina 2.

RYCINA 2. Przebiegi czasowe prądów jonowych przy ustalonym napięciu na błonie.

Widać z niego, że po przyłożeniu do błony stałego w czasie napięcia V_m., przepływa przez nią prąd całkowity zilustrowany krzywą 1 (ze względu na bardzo małą stałą czasową błony na wykresach prąd pojemnościowy jest niewidoczny). Następnie stosując specyficzny bloker, np. dla jonów sodu, rejestruje się prąd całkowity pomniejszony o jego składową sodową - krzywa 2. Krzywa 3 odpowiada różnicy wartości prądów z krzywej 1 i krzywej 2 (przy założeniu, że prąd upływu jest zaniedbywalnie mały) i przedstawia prąd sodowy przenoszony przez wszystkie kanały sodowe na powierzchni błony znajdującej się między elektrodami pomiarowymi. Na powierzchni takiej znajduje się duża liczba kanałów, a więc o ich indywidualnych własnościach można wnioskować tylko pośrednio z charakterystyk prądowo-napięciowych uzyskanych w konkretnych warunkach eksperymentalnych. Z metodą voltage-clamp można zapoznać się z podręcznika "Cellular Biophysics" autorstwa T. S. Weissa [68]. Dopiero opracowana przez Nehera i Sakmanna [52] metoda patch-clamp umożliwiła wykonywanie pomiarów na pojedynczych kanałach. Metoda ta w ogólności polega na doprowadzeniu do trwałego mechanicznego i elektrycznego (kontaktu końcówki pipety szklanej (o średnicy około 1m i oporności kontaktu ponad 10⁹ ohm) do badanej błony komórki i rejestracji prądów elektrycznych przepływających przez przylegającą do pipety powierzchnię błony, przy ustalonym napięciu miedzy elektrodami pomiarowymi. Dzięki temu, że na tak małej powierzchni mogą znajdować się tylko pojedyncze kanały, możliwe jest uzyskiwanie charakterystyk transportowych pojedynczych kanałów. Istnieje kilka odmian tej metody. Schematycznie jest to przedstawione na rycinie 3.

RYCINA 3. Schemat do pomiaru prądów jonowych metodą patch- clamp.

Nie będziemy tu jednak zajmować się szczegółami tej metody, które można znaleźć w bardzo dobrej monografii Sakmanna i Nehera [60].

Badania tego typu potwierdziły wysoką selektywność poszczególnych rodzajów kanałów dla poszczególnych jonów. Uzyskana z tych pomiarów szybkość przenoszenia jonów, ~10⁷ jonów na sekundę (ilość jonów przechodzących przez kanał w ciągu 1 sekundy), okazała się zbliżona do wartości obserwowanej w swobodnej dyfuzji w wodnych roztworach elektrolitów o grubości warstwy równej grubości błony. Tak duża wartość szybkości przenoszenia jonów w kanałach jonowych wskazuje na to, że mechanizm transportu nie może być mechanizmem nośnikowym, który ma miejsce w aktywnym transporcie realizowanym przez występujące w błonach pompy jonowe czy biernym transporcie wymiennym (np. realizowanym w przypadku anionów przez białko pasma 3 w błonie erytrocytów). Kanały w błonach pobudliwych są wysoce selektywne dla kationów jednowartościowych (Na⁺ i K⁺). Selektywność ta nie może więc być wynikiem oddziaływania elektrostatycznego z ładunkami elektrycznymi wewnętrznej powierzchni kanału. Jest natomiast skutkiem oddziaływania ze zwróconymi do wnętrza kanału resztami chemicznymi białek tworzących kanał [2]. Z szeroko prowadzonych badań biochemicznych wiemy już dziś dość dobrze jakie białka tworzą w błonach odpowiednie rodzaje kanałów. Znana jest ich sekwencja aminokwasowa i ogólna struktura trzecio- i czwarto-rzędowa.. Wiadomo jakie części białka kanałowego są odpowiedzialne za tworzenie uwodnionej pory, jakie tworzą filtr odpowiedzialny za selektywność kanału oraz jakie mogą być sensorem napięcia odpowiedzialnym za zmianę stanu przewodzącego w nieprzewodzący (i odwrotnie) w kanałach napięciowo-zależnych. Ze względu na bardzo rozległą literaturę szczegółową z tego zakresu nie będziemy jej tu cytować, lecz odsyłamy czytelnika do najnowszego wydania bardzo dobrej monografii [28] i prac przeglądowych [61,71].

Poszczególni badacze, którzy opracowywali opis teoretyczny transportu jonów w otwartych kanałach jonowych, musieli w oparciu o informacje z badań biochemicznych oraz z uzyskanych eksperymentalnie charakterystyk transportowych kanałów, tworzyć określone ich modele. Do niedawna brak było bowiem bezpośrednio uzyskanych doświadczalnie obrazów kanałów jonowych. Pierwsze doniesienie o uzyskaniu takich obrazów ukazały się pod koniec lat dziewięćdziesiątych ubiegłego wieku i pierwszych latach dwutysięcznych. Uzyskano obrazy rentgenograficzne kanałów potasowych, chlorowych, zależnych od naprężenia mechanicznego, receptora acetylocholiny oraz kanałów wodnych (aquaporyn). Szczególne znaczenie ma tu praca [16], której autorom udało się wykrystalizować białko kanału potasowego, KcsA, z błony bakterii Streptomyces lividans , i uzyskać trójwymiarowy obraz rentgenograficzny tego kanału, ze zdolnością rozdzielczą 0,32 nm. Uzyskane w tej pracy wyniki zostały potwierdzone w pracach [47,73] ze zdolnością rozdzielczą 0,2 nm. Pomimo tego, że kanał KcsA nie jest napięciowo-zależny i jego obraz odpowiada stanowi nieprzewodzącemu, to stał się on podstawą do tworzenia realistycznych modeli kanałów jonowych (głównie potasowych) [61,66] (i literatura cytowana w tych pracach przeglądowych).

Ogólny schemat potasowego kanału jonowego, jaki można w oparciu o te prace naszkicować, przedstawia rycina 4.

RYCINA 4. Schematyczny przekrój kanału jonowego.

Widać z niego, że przekrój poprzeczny pory wodnej zmienia się wzdłuż osi kanału. W części kanału zwróconej do otoczenia komórki występuje odpowiedzialny za jego selektywność filtr o długości 1,2 nm i średnicy 0,3 nm. W części środkowej występuje stosunkowo szeroka wnęka o długości około 1,0 nm, mogąca pomieścić kilkadziesiąt cząsteczek wody. W części kanału zwróconej do wnętrza komórki (o długości około 2,0 nm) zlokalizowane są podjednostki białka kanałowego odpowiedzialne za zamykanie i otwieranie kanału (bramka kanału); w stanie zamkniętym najmniejsza średnica tej części pory wynosi 0,24 nm, podczas gdy średnica jonu K⁺ jest równa 0,26 nm. Ścianki tej części pory są hydrofobowe. Podane tu dane liczbowe pochodzą z pracy [12]. Bezpośrednio z obrazu rentgenowskiego widać, że w filtrze mogą znajdować się co najwyżej dwa jony potasu (rozdzielone cząsteczką wody). W środkowej wnęce kanału może znajdować się trzeci jon potasu. Takie rozmieszczenie jonów potasu w kanale potwierdzane jest przez modelowanie na gruncie dynamiki Brownowskiej [11] oraz dynamiki molekularnej [1,6,61] ( i cytowana w tych pracach literatura).

Szczegółowe badania białka tworzącego różne kanały potasowe wykazują, że jego część tworząca filtr jest niezmiennikiem dla wszystkich kanałów potasowych [28,42,47]. Utworzony on jest z odcinków łańcuchów polipeptydowych (dwóch lub czterech podjednostek białka kanałowego) o sekwencji TVGYG. Dzięki temu w filtrze można wyróżnić cztery centra (S1, S2, S3 i S4), w których atomy tlenu reszt karbonylowych dokładnie odpowiadają wiązaniom koordynacyjnym jonów potasu i mogą zastępować atomy tlenu cząsteczek wody z jego otoczki hydratacyjnej [46]. Z badań rentgenograficznych [73] i modelowania metoda dynamiki molekularnej [4] wynika, że występuje jeszcze jedno centrum (S0) w obszarze zewnętrznego wejścia do kanału. Ilustruje to schematycznie rycina 5.

RYCINA 5. Schematyczne rozmieszczenie jonów K⁺ (
) i cząsteczek wody (
) w filtrze kanału jonowego.

Obecność takiego niezmienniczego filtra we wszystkich kanałach potasowych pozwala na opracowanie jednolitego opisu teoretycznego transportu jonów we wszystkich kanałach potasowych w stanie otwartym. A jak zrobiono to w pracy [15] opis taki może być stosowany również do kanałów wapniowych.

3. TRANSPORT JONÓW W KANAłACH

Opracowując opis transportu jonów w kanałach trzeba brać pod uwagę zarówno rozmiary geometryczne pory kanału jak i rodzaj reszt chemicznych białka kanałowego znajdujących się na ściankach pory. Nie należy przy tym zapominać, że obraz kanału jonowego uzyskany z badań strukturalnych jest obrazem statycznym (uśrednionym po pewnym czasie), natomiast rzeczywista struktura białka kanałowego jest zmienna w czasie. Uwzględnienie tego ostatniego faktu, jakkolwiek bardzo istotne, w dotychczasowych teoriach transportu w kanałach jonowych nie miało miejsca (za wyjątkiem modelowania w oparciu o dynamikę molekularną).

Zapoczątkowany przez Goldmana [26], i następnie rozwijany w wielu pracach, elektrodyfuzyjny opis kontynualny był i w dalszym ciągu jest często stosowany do opisu transportu jonów w otwartych kanałach jonowych. Podstawy tego opisu przedstawiamy w Dodatku A. Szczegółową literaturę można znaleźć w monografiach [28,64]. Łatwo zauważyć, że jest to teoria średniego pola. Tak naprawdę, w związku z założeniami jakie trzeba było dodatkowo przyjmować przy jej opracowaniu, można ją stosować tylko do opisu transportu jonów w kanałach o wystarczająco dużej średnicy pory kanału i dla roztworów o rozcieńczeniu zapewniającym brak oddziaływań między transportowanymi jonami. W takich kanałach stężenie jonów, jako wielkość statystyczna, jest dokładnie określone. Przenikalność elektryczna i współczynniki dyfuzji jonów we wnętrzu kanału są równe odpowiadającym im wielkościom w roztworze graniczącym z błoną. Warunki te nie są jednak spełnione dla kanałów, których struktura jest bliska modelowi przedstawionemu wyżej. Eisenberg i jego współpracownicy [9,10,17,18,20,24,57,62] oraz Kurnikova z jej współpracownikami [8, 27,35,44], rozwinęli trójwymiarową teorię elektrodyfuzyjną opartą na równaniu Nernsta-Plancka i równaniu Poissona dla potencjału oddziaływań elektrostatycznych. Teoria ta nazywana jest teorią PNP (Poisson-Nernst-Planck). Jest to w dalszym ciągu teoria średniego pola i jak wykazano w pracach [14,49] nie może mieć zastosowania w kanałach o rozmiarach jak na schemacie wyżej prezentowanym. Można ją stosować tylko dla kanałów o rozmiarach przekraczających dwukrotną wartość promienia Debye'a. Teoria PNP nie może być stosowana do opisu transportu jonów w kanałach tu rozpatrywanych również z tego powodu, że średnia w czasie ilość jonów obserwowana w tych kanałach (o czym była mowa wyżej) jest porównywalna z fluktuacjami tej ilości i w związku z tym traci sens pojęcie ich stężenia. Na problem ten zwrócono uwagę w pracach [45,62]. Nie pociągnęło to jednak za sobą konsekwencji w postaci uwzględnienia tego faktu w proponowanych teoriach, a w przypadku drugiej pracy tu cytowanej problem ten jest omijany przez dokonywanie uśrednień w długim czasie w sposób nie do końca zrozumiały. W nowszych pracach grupa Eisenberga uogólnia równania PNP przez dodanie do potencjału chemicznego jonów "excesu" odpowiedzialnego za oddziaływanie między jonami transportowanymi przez kanał i ewentualnego nieelektrostatycznego oddziaływania jonów ze ściankami pory kanału [22,23].

Oparty o teorie PNP opis transportu jonów w kanałach jonowych zawodzi również w opisie obserwowanego doświadczalnie nasycenia strumienia jonów w zależności od stężenia tych jonów w graniczącym z błoną roztworze, przy ustalonym potencjale błonowym. Według teorii PNP zależność strumienia od stężenia powinna być liniowa.

Warto tu jeszcze raz podkreślić, że stosowanie kontynualnego opisu transportu jonów w kanałach (porach) o rozmiarach atomowych jest z natury rzeczy niewłaściwe. Stosowane do charakterystyki tych kanałów makroskopowe parametry takie jak współczynnik dyfuzji, (równoważnie ruchliwość jonów), stężenie i przenikalność elektryczna, wzięte z opisu kontynualnego nie mają racjonalnego usprawiedliwienia. Potwierdza to praca poświęcona symulacjom Monte Carlo podwójnej warstwy elektrycznej w nano-porach o rozmiarach około 2 nm [69,70].

Powyższe uwagi o kontynualnym opisie transportu jonów w otwartych kanałach jonowych, opartym o teorię elektrodyfuzji (teoria PNP), wskazują że jest on nieadekwatny dla kanałów o rozmiarach obserwowanych doświadczalnie. Przypadkowa zgodność tej teorii z doświadczeniem dla konkretnego kanału [56], może być wynikiem znoszenia się efektów przyjmowania błędnych wartości parametrów charakteryzujących kanał i błędnych założeń w fizyce kanałów [15].

Fundamentalnym modelem aspirującym do realistycznego opisu transportu jonów w kanałach z jakimi spotykamy się w błonach pobudliwych jest dynamika molekularna (MD) [1,5,11,41,51,59]. Jony i inne cząsteczki (cząsteczki wody i białka kanałowego) są tutaj traktowane indywidualnie. Rozwiązywane są równania ruchu Newtona dla jonów oddziałujących z innymi jonami, cząsteczkami wody oraz ściankami kanału Niestety, czas potrzebny do obliczenia wielu własności kanałów (w tym ich przewodnictwa) jest jak dotychczas bardzo długi (dla najszybszych komputerów są to lata). W tej sytuacji jeśli nawet będziemy mieć w pełni realistyczny model kanału i poprawnie, z punktu widzenia fizyki, będziemy mogli opisać oddziaływania między cząsteczkami w kanale, to wspomniany wyżej czas potrzebny do uzyskania wyników uniemożliwia dziś wykorzystywanie dynamiki molekularnej do opisu transportu jonów w nano-kanałach .

Modelem mniej fundamentalnym, ale nadal opisującym ruch indywidualnych jonów w kanałach, jest dynamika Brownowska (BD). W celu ograniczenia ilości równań, siłę działającą na dany jon (pochodzącą od cząsteczek wody i ścianek kanału) przedstawia się jako sumę deterministycznej siły tarcia oraz losowej siły (biały szum) o średniej wartości równej zero. Przechodzimy w ten sposób od deterministycznych równań Newtona do stochastycznych równań Langevina,

, (2)

gdzie m_i, q_i, v_i, to odpowiednio masa, ładunek i prędkość i-tego jonu, a E natężenie pola elektrycznego. Siła tarcia -m_iγ_iv_i, (gdzie γ_i jest współczynnikiem tarcia na jednostkę masy) i siła stochastyczna F_r są rezultatem przypadkowych zderzeń jonu z cząsteczkami wody i ścianek pory kanału. F_s jest siłą krótkozasięgowego nieelektrostatycznego oddziaływania jonów z kanałem. Natężenie pola elektrycznego, odpowiedzialnego za działającą na jon siłę elektryczną, obliczane jest numerycznie dla każdego punktu kanału z równania Poissona w formie

, (3)

gdzie
= (x,y,z) jest wektorem położenia punktu, w którym odpowiednia wielkość jest określona, ρ jest łączną gęstością ładunków ruchliwych jonów i ładunków związanych z białkiem kanałowym,  jest potencjałem pola elektrycznego,  - przenikalnością elektryczną a
= (
) - operatorem gradientu. Do otrzymanego w ten sposób natężenia pola dodaje się pole zewnętrzne związane z potencjałem błonowym.

W pierwszej pracy [13], w której zastosowano dynamikę Brownowską do opisu transportu jonów w kanałach jonowych, zakładano jednowymiarowy charakter ruchu jonów. Było to założenie odległe od realistycznego modelu kanałów jonowych. Prace publikowane od roku 1998, głównie przez grupę fizyków z Australian National University (Canberra), zawierają już obliczenia numeryczne w trójwymiarowej geometrii kanałów. Odsyłacze do szczegółowych publikacji poświeconych tym zagadnieniom można znaleźć w obszernych pracach przeglądowych [12,37,38,39].

Potrzebne do rozwiązania parametry (np. przenikalność elektryczną czy współczynnik dyfuzji) brane są z symulacji opartych o dynamikę molekularną, ale często stosowane jest dopasowywanie ich wartości w oparciu o zasadę optymalizacji wyników rozwiązywanego równania [15]. Rozmiary geometryczne pory kanału przyjmowane są w oparciu o doświadczalnie otrzymane obrazy konkretnego kanału lub z symulacji opartych o dynamikę molekularna dla konkretnego białka kanałowego o określonej doświadczalnie charakterystyce. W metodzie BD, równanie Langevina jest rozwiązywane wielokrotnie dla określenia trajektorii wszystkich jonów. W tym celu w bardzo krótkich odstępach (krokach) czasu, kilku femtosekund (10^-15 s), równanie Langevina jest całkowane dla określenia prędkości wszystkich jonów i ich położenia przed następnym krokiem. Powtarzając tą procedurę przez dostatecznie długi czas, zwykle kilku mikrosekund (10^-6 s), określa się liczbę jonów (n) przechodzących przez kanał w określonym czasie (t). Pozwala to na obliczenie strumienia jonów,

. (4)

Szczegóły tej metody można znaleźć w pracy przeglądowej [37]. Uzyskane w ten sposób strumienie, dla różnych wartości potencjałów błonowych przy ustalonym stężeniu jonów lub różnych wartościach stężeń jonów w środowisku przylegającym do błony przy ustalonym potencjale błonowym, pozwalają określić zarówno charakterystyki prądowo-napięciowe, jak i charakterystyki prądowo-stężeniowe. Charakterystyki te mogą być konfrontowane z danymi doświadczalnymi.

Autorzy pracy [15] deklarują we wstępie do niej, że przy opracowywaniu modelu na gruncie dynamiki Brownowskiej nie przyjmowali ad hoc potencjałów chemicznych jonów ani dopasowywanych do doświadczeń wartości parametrów opisywanego kanału. Wydaje się jednak, w oparciu o to co wyżej zostało powiedziane, że jest to deklaracja trochę na wyrost. Optymalizacja parametrów modelu kanału, jak i obliczenia ich wartości na gruncie dynamiki molekularnej, nie są wolne od koniecznych przybliżeń (np. traktowanie wody w porze kanału jako kontinuum, przyjęcie dla względnej przenikalności elektrycznej białka kanałowego wartości równej 2, czy też traktowanie cząsteczki białka kanałowego jako struktury statycznej).

Mimo daleko idących uproszczeń, opis transportu jonów w nano-kanałach, oparty na dynamice Brownowskiej, wyjaśnia więcej obserwowanych doświadczalnie charakterystyk kanałów jonowych niż teoria PNP. W szczególności przewiduje zgodne z doświadczeniem charakterystyki prądowo-napięciowe i prądowo-stężeniowe (w tym obserwowane doświadczalnie nasycenie strumienia jonów przy wzroście ich stężenia w roztworze przylegającym do błony [42,45], spowodowane brakiem zależności czasu przejścia jonu przez filtr selektywny od stężenia [5,12,37,38,59].

Opis transportu jonów na gruncie fenomenologicznej teorii BD jest jednak ciągle grubym przybliżeniem i nie wyjaśnia wszystkich obserwowanych doświadczalnie charakterystyk kanałów jonowych (np. selektywności kanałów dla kationów jednowartościowych). Jeśli uświadomimy sobie, że białka to struktury dynamiczne, których pory przewodzące jony mają przekroje poprzeczne o rozmiarach atomowych, to staje się zrozumiałym, że wykorzystanie do opisu ich funkcji, makroskopowych parametrów statystycznych (takich jak przenikalność elektryczna i współczynnik dyfuzji we wnętrzu pory kanału) jest słabo uzasadnione i może stanowić istotne ograniczenie przydatności dynamiki Brownowskiej do opisu transportu jonów w kanałach. Również, jak wynika to z prac [6,63], niedookreślone jest pojęcie przenikalności elektrycznej cząsteczek białka i roztworu tuż przy ich powierzchni [21]. W szczególności nie można cząsteczki białka scharakteryzować uśrednioną przenikalnością elektryczną (szacowana z różnych obliczeń jej wartość w różnych punktach cząsteczki jest różna; równocześnie zależy ona od przyjętej metody obliczeń). Powszechnie traktuje się też białko kanałowe jako strukturę równowagową i w tej sytuacji jego przenikalność elektryczna jest niezależna od czasu. Tymczasem kanały jonowe to struktury nierównowagowe, w których poruszające się jony mogą indukować zmienność w czasie przenikalności elektrycznej białka kanałowego [6]. Omawiany tu problem przenikalności elektrycznej kanałów jonowych w równym stopniu dotyczy modelowania w oparciu o BD jak i teorii PNP. Uwaga ta dotyczy również modelowania w oparciu o dynamikę molekularną [50].

Warto zwrócić uwagę na jeszcze jeden problem. Mianowicie w dynamice Brownowskiej opisuje się ruch indywidualnych jonów. Wyniki prac doświadczalnych [47] jak i modelowanie w oparciu o dynamikę molekularną [3,5,64] wskazują jednak, że w kanale jony potasu przemieszczają się kolektywnie wraz z rozdzielającą je cząsteczką wody - przechodzą z centrów S1 i S3 do centrów S2 i S4. Taki kolektywny transport nie może być opisany w prosty sposób w ramach dynamiki Brownowskiej [72]. Próbę kinetycznej teorii takiego transportu przedstawiono w pracach Nelsona [53,54,55]. Przyjęto, że barierą dla transportu jest wejście i wyjście jonów do i z kanału, przy równoczesnym braku bariery przy przechodzeniu przez kanał (co jest zgodne z modelowaniem molekularnym). W pracach tych uzyskano potwierdzenie dla obserwowanego nasycenia w charakterystykach prądowo-stężeniowych. Również z uwagi na fakt, że rozmiary jonów są porównywalne z rozmiarami cząsteczek wody, traktowanie jonów w kanale jako cząstki Browna (jak to się zakłada w teorii BD) nie jest w pełni uzasadnione [27].

Chcielibyśmy się odnieść do jeszcze jednej kwestii. W wielu podręcznikach z fizjologii i biofizyki, w rozdziałach poświęconych impulsowi nerwowemu, ciągle operuje się pojęciem stałej przenikania, P_i, błony komórki nerwowej dla poszczególnych jonów typu i. . W szczególności stała przenikania P_i jest wykorzystywana do oceny selektywności kanałów jonowych [28,43,67]. Przebieg w czasie potencjału czynnościowego wyjaśnia się, zależną od potencjału błonowego, zmianą stałej przenikania dla jonów sodu,
, oraz jonów potasu,
, odwołując się do wzoru Goldmana-Hodgkina-Katza na dyfuzyjny potencjał spoczynkowy, w którym te stałe przenikania występują. Należy jednak pamiętać, że wyprowadzony przez Goldmana [26] wzór jest spełniony dla błon jednorodnych, w których jony podlegają elektrodyfuzji przez całą powierzchnię błony. Występujące w tym wzorze stałe przenikania, P_i, są zdefiniowane zależnością:

, (5)

gdzie K_i jest współczynnikiem podziału danego jonu między fazą błony i przylegającym do niej roztworem elektrolitu (stałym dla całej błony), D_i współczynnikiem dyfuzji danego jonu (stałym dla całej błony) oraz d grubością błony.

Ponieważ jony w błonach pobudliwych przenikają przez zależne od potencjału błonowego kanały jonowe, to pojęcie stałej przenikania błony, dla pojedynczych kanałów, traci sens. Mianowicie, jak to wynika z powyższych danych o strukturze kanałów jonowych, nawet przy założeniu, że występujące po prawej stronie zależności (5) parametry są określone, to nie można przyjmować ich niezależności od współrzędnych, chociażby ze względu na zmianę przekroju porzecznego kanału. Dodatkowo, skoro pojęcie stężenia jonów w kanałach jonowych jest nieokreślone, to nieokreślonym staje się pojęcie współczynnika podziału, K_i. Mierzalnymi i określającymi przechodzenie jonów przez błonę wielkościami są przewodności błony dla poszczególnych jonów. Wielkości te występują w równaniu na prąd płynący przez błonę w stanie pobudzenia [31]. Przewodność jonowa błony dla jonu i-tego rodzaju jest określona przez zależność

G_i = n_i p_i g_i, (6)

gdzie n_i jest ilością kanałów danego rodzaju na powierzchni błony (przykładowo, w wycinku błony aksonu kałamarnicy Loligo o powierzchni 1mikrometr kwadratowy znajduje się około 360 kanałów sodowych i 80 potasowych); p_i zależnym od potencjału błonowego prawdopodobieństwem otwarcia kanału jonowego (danego rodzaju) oraz g_i przewodnością pojedynczego kanału (danego rodzaju). Zmiany w czasie przewodnictw jonów sodu i potasu (zależnych od potencjału błonowego) określają przebieg potencjału czynnościowego.

Na koniec chcielibyśmy jeszcze raz zwrócić uwagę na fundamentalny problem występujący zarówno w modelach ciągłych typu PNP jak i w dynamice Brownowskiej. W kanałach zawierających jednocześnie kilka jonów istotne wydaje się uwzględnienie oddziaływań między nimi. W równaniu Langevina, przypadkowe zderzenia jonu z cząsteczkami wody i ścianek kanału jest przedstawione jako suma deterministycznej siły tarcia i siły czysto losowej. Związki między siłą tarcia a fluktuacjami siły losowej są opisywane na gruncie teorii fluktuacyjno-dyssypacyjnej. Zakłada ona znajdowanie się układu w równowadze termodynamicznej i co więcej brak oddziaływań pomiędzy cząstkami Browna. Wtedy współczynnik dyfuzji D_i (mierzący wielkość fluktuacji) spełnia relację Einsteina, D_i=kT/m_iγ_i, gdzie T jest temperaturą układu. Jeżeli uwzględnimy oddziaływanie jonów, to siły losowe działające na poszczególne jony przestają być niezależne. Problematyczny staje się też wtedy sam podział siły na część deterministyczną i losową.

W pracy [62], autorzy twierdzą, że roztwory w kanałach są bardzo rozcieńczone i wobec tego można zaniedbać korelacje pomiędzy siłami losowymi działającymi na poszczególne jony (aczkolwiek explicite rozważają oni oddziaływania pomiędzy jonami). Następnie wyprowadzają oni odpowiednie równanie elektrodyfuzji z samouzgodnionym polem elektrycznym będącym rozwiązaniem równania Poissona. Zauważmy jednak, że roztwory w kanałach, w porównaniu do rozcieńczonych roztworów swobodnych, gdzie jony znajdują się daleko od siebie, nie są rozcieńczone. Pomimo tego, że w kanale znajduje się tylko kilka jonów, to ze względu na atomowe rozmiary kanałów, jony

znajdują się blisko siebie i nie można zaniedbać oddziaływań między nimi. Co więcej, koncepcja pola samouzgodnionego używa pojęcia stężenia jako wielkości statystycznej.

Przy tak małej ilości jonów w kanale, fluktuacje stężenia są porównywalne z jego wielkością.

Inne podejście zawarte jest w pracy [7]. Analizowany jest tam ruch oddziałujących jonów w roztworach elektrolitów. W odpowiednim równaniu Langevina, siła tarcia przybiera postać całki zależnej od historii. Wprowadzenie członu tarciowego z pamięcią jest również stosowane w przypadku kiedy rozmiar cząstki Browna jest porównywalny z rozmiarami otaczających ją cząstek [34] co ma miejsce w kanałach jonowych.

Uwzględnienie oddziaływań między jonami w opisie ich transportu w kanałach wymaga dogłębnych badań. Oddziaływania między jonami różnego rodzaju prowadzi do zależności między strumieniami. Natomiast oddziaływanie między jonami tego samego rodzaju w obrębie jednego kanału nie prowadzi oczywiście do oddziaływań między kanałami. Zostało to wykorzystane we wzorze (6), gdzie stosujemy zasadę addytywności.

Podsumowując, można chyba stwierdzić, że jedynie mikroskopowy opis funkcjonowania kanałów (np. w oparciu o dynamikę molekularną) może w pełni wyjaśnić mechanizmy ich funkcjonowania. By jednak było to możliwe, potrzebny jest dalszy rozwój technik obliczeniowych i pełniejsza wiedza o strukturze molekularnej (na poziomie atomowym) kanałów jonowych, a także rozwój fizyki układów o odpowiadających im rozmiarach.

DODATEK A

Równania elektrodyfuzji

Opis transportu jonów przez błony komórkowe w oparciu o teorię Goldmana [26] bazuje na jednowymiarowych równaniach elektrodyfuzji Nernsta- Plancka (NP) dla strumieni jonów,

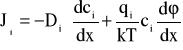
, (A1)

oraz równaniu Poissona,

, (A2)

gdzie D_i jest współczynnikiem dyfuzji jonów i-tego rodzaju, c_i ich stężeniem, k - stałą Boltzmanna, T - temperaturą bezwzględną, q_i - ładunkiem jonu,  - potencjałem elektrycznym, a
- ładunkiem związanym z błoną. Równanie NP może być uzyskane na gruncie termodynamiki procesów nieodwracalnych lub z rozważań statystycznych (Dodatek B). W opisie tym nie uwzględnia się oddziaływania między jonami ruchliwymi oraz oddziaływania nieelektrostatycznego jonów z błoną.

Uwzględnienie tego ostatniego oddziaływania wymagałoby obecności w równaniu na strumień jonów, J_i, dodatkowego członu wyrażającego energię tego oddziaływania. W tym przypadku uogólnione równania NP mają następującą postać:

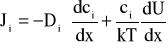
, (A3)

gdzie
, q_i jest energią jonu w polu elektrycznym, a W_i - energią oddziaływania nieelektrostatycznego jonu z błoną [35,41,58,59]. Dla kanałów szerokich, wielojonowych, o średnicy przekraczającej kilka promieni Debye'a, oddziaływanie nieelektrostatyczne jonów z kanałem można zaniedbać. Równocześnie dla kanałów tego typu usprawiedliwione jest stosowanie pojęcia stężenia jonów.

Zakładając, że prawa strona równania (A2) jest równa zeru (elektroneutralność), a więc przyjmując stałość natężenia pola elektrycznego w błonie i dodatkowo przyjmując, że mamy do czynienia ze stanem stacjonarnym, równania (A1) możemy scałkować. Otrzymamy wtedy wyrażenie na strumień, J_i,

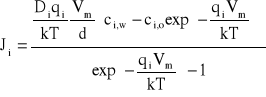
, (A4)

gdzie d jest grubością błony, V_m. - potencjałem błonowym, c_i,w - stężeniem jonów w błonie na granicy z wnętrzem komórki, a c_i,o - stężeniem jonów w błonie na granicy z otoczeniem komórki.

Przyjmując, że prąd elektryczny w błonie jest przenoszony tylko przez biernie transportowane jony Na⁺, K⁺ i Cl^-, równanie (A4) pozwala, dla stanu stacjonarnego komórki (wypadkowe natężenie prądu jest równe zeru), wyprowadzić zależność na potencjał błonowy V_m., nazywaną równaniem Goldmana-Hodgkina-Katza,

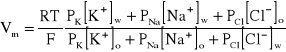
, (A5)

gdzie: P_K, P_Na, P_Cl to zdefiniowane wcześniej stałe przenikania dla poszczególnych jonów, F - stała Faraday'a, R - stała gazowa, a nawiasy kwadratowe oznaczają stężenia molowe odpowiednich jonów we wnętrzu komórki (w) i jej otoczeniu (o).

DODATEK B

Równanie Smoluchowskiego

Równanie NP można otrzymać z rozważań statystycznych, które zgodnie z pracami Einsteina i Smoluchowskiego opierają się na teorii ruchów Browna. Zakłada się, że jony przechodząc przez błonę (kanały) doznają dużego tłumienia, co usprawiedliwia zaniedbanie w równaniu Langevina (2) członu inercyjnego (
). Otrzymuje się wtedy zredukowane równanie Langevina,

, (B1)

gdzie prędkość jonu jest proporcjonalna do sumy sił. Aby równanie (B1) miało sens, zakłada się ponadto, że siły zewnętrzne nie zmieniają się na drodze gdzie występuje tłumienie. W wąskich kanałach jest to wątpliwe założenie - przekrój poprzeczny takich kanałów nie jest stały i wobec tego oddziaływanie jonów ze ściankami kanału zmienia się na niewielkich odległościach.

Jon jako cząstka Browna porusza się chaotycznie i jego trajektorie są wielkościami stochastycznymi. Położenie i prędkość jonu w takiej sytuacji można określić tylko z pewnym prawdopodobieństwem, przedstawionym w równaniach Fokkera-Plancka. W przypadku ruchu z dużym tłumieniem, prawdopodobieństwo znalezienia cząstki w miejscu o określonych współrzędnych i w określonym czasie, p(x,t), można otrzymać rozwiązując równanie Smoluchowskiego, które jest szczególnym przypadkiem równania Fokkera-Plancka. Równanie Smoluchowskiego ma następującą postać:

, (B2)

gdzie F_i=q_iE + F_s. Dla szerokich wielojonowych kanałów prawdopodobieństwo p_i można zastąpić stężeniem i wtedy równanie Smoluchowskiego przechodzi w równanie NP, gdy skorzystamy z równania ciągłości,

, (B3)

przy założeniu, że D_i nie zależy od x.

LITERATURA

[1] Allen TW, Kuyucak S, Chung S-H . Molecular dynamic study of the KcsA

potasium channel. Biophys J 1999; 77: 2502-2516.

[2] Beckstein O, Sansom MSP . The influence of geometry, surface character, and

flexibility on the permeation of ions and water through biological pores. Phys Biol

2004; 1: 42-52.

[3] Berneche S, Roux B. Molecular dynamics of the KcsA K⁺ channel in a bilayer

membrane. Biophys J 2000; 78: 2900-2917.

[4] Berneche S, Roux B. Energetics of ion conduction through the K⁺ channel. Nature

2001; 414: 73-77.

[5] Berneche S, Roux B. A microscopic view of ion conduction through the K⁺ channel.

Proc Nat Acad Sci 2003; 100: 8644-8648.

[6] Burykin A, Schutz CN, Villa J, Warshel A. Simulation of ion current in realistic

models of ion channels: The KcsA potassium channel. Protein 2002; 47: 2502-2516.

[7] Canales M, Sese G. Generalized Langevin dynamics simulations of NaCl

electrolyte solutions. J Chem Phys 1998; 109: 6004-6011.

[8] Cardenas AD,Coalson RD, Kurnikova MG. Tree-dimensional

Poison-Nernst-Planck theory studies: Influence of membrane electrostatics on gramicidin

A channel conductance. Biophys J 2000; 79: 80-93.

[9] Chen D, Eisenberg RS. Charges, currents and potentials in ionic channels of one

conformation. Biophys J 1993; 64: 1405-1421.

[10] Chen D, Eisenberg RS. Flux, coupling, and selectivity in ionic channels of one

conformation. Biophys J 1993; 65: 727-746.

[11] Chung SH, Allen TW, Kuyucak S. Conducting-state properties of the KcsA potassium

channel from molecular and Brownian dynamics simulations. Biophys J 2002; 82: 628-

645.

[12] Chung SH, Kuyucak S. Recent advances in ion channel research. Biochim Biophys Acta

2002; 1565: 267-286.

[13] Cooper K, Jakobson E, Wolynes P. The theory of ion transport through membrane

channels. Prog Biophys Molec Biol 1985; 46: 51-96.

[14] Corry B, Kuyucak S, Chung SH. Tests of continuum theories as models of ion channels.

II. Poisson-Nernst-Planck theory versus Brownian-dynamics. Biophys J 2000; 78: 2364-

2381.

[15] Corry B, Allen TW, Kuyucak S, Chung SH. Mechanisms of permeation and selectivity in

calcium channels. Biophys J 2001; 80: 195-214.

[16] Doyle DA, Cabral JM, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, Chait BT,

MacKinnon R. The structure of the potassium channel: Molecular basis of K⁺ conduction

and selectivity. Science 1998; 280: 68-77.

[17] Eisenberg RS. Ionic channels in biological membranes - electrostatic analysis of a natural

nanotube. Contemp Phys 1998; 39: 447-466.

[18] Eisenberg RS. Ionic channels: natural nanotubes descrbed by the drift diffusion

equations. Superlattices and Microstructures 2000; 27: 545-549.

[19] Eisenberg RS. Permeation as a diffusion process. [w] DeFelice LJ [red.] Biophysics

Textbook On-Line. Biophysical Society Homepage 2000;

http://biosci.umn.edu/biophys/BTOL/.

[20] Eisenberg RS. Protein, channels and crowded ions. Biophys Chem 2003; 100: 507-517.

[21] Finken RV, Ballengger V, Hansen JP. Onsager model for a variable dielectric permeation

near an interface. Mol Phys 2003; 101; 2559-2568.

[22] Gillespie D, Eisenberg RS. Physical descriptions of experimental selectivity

measurements in ion channels. Eur Biophys J 2002; 31: 454-466.

[23] Gillespie D, Nonner W, Eisenberg RS. Coupling Poisson-Nernst-Planck and density

functional theory to calculate ion flux. J Phys: Condens Matter 2002; 14: 12129-12145.

[24] Gillespie D, Nonner W, Henderson D, Eisenberg RS. A physical mechanism for large ion

selectivity of ion channels. Phys Chem Chem Phys 2002; 4: 4763-4769.

[25] Gilson MK. Introduction to continuum electrostatics with molecular applications.2000;

[Na stronie inter.] http://gilsolab.umbi.umd.edu

[26] Goldman DE. Potential, impedance, and rectification in membranes. J Gen Physiol 1943;

27: 37-60.

[27] Graf P, Kurnikova MG, Coalson RD, Nitzan A. Comparison of dynamic lattice Monte

Carlo simulations and the dielectric self-energy Poisson-Nernst-Planck continuum

theory for model ion channels. J Phys Chem B 2004; 108: 2006-2015.

[28] Hille B. Ion channels of excitable membranes. Sunderland, Massachusetts USA: Sinauer

Asociates 2001.

[29] Hodgkin AL, Katz B. The effect of sodium ions of the electrical activity of the giant axon

of the squid. J Physiol 1949; 108: 37-77.

[30] Hodgkin AL, Huxley AF. A quantitative description of membrane current and its

application to conduction and excitation of nerve. J Physiol 1952; 117: 500-544.

[31] Hodgkin AP, Huxley AF, Katz B. Measurement of current-voltage relations in the giant

axon of Loligo. J Physiol 1952; 116: 424-448.

[32] Hoyles M, Kuyucak S, Chung SH. (1998). Computer simulation of ion conductance in

membrane channels. Phys Rev E 1998; 58: 3654-3661.

[33] Huxley AF. From overshoot to voltage clamp. TRENDS in Neuroscieces 2002; 25: 553-

558.

[34] Kubo R. The fluctuation-dissipation theorem. Rep Prog Phys 1966; 29: 255-284.

[35] Kurnikova MG, Coalson RD, Graf P, Nitzan A. A lattice relaxation algorithm for three-

dimensional Poisson-Nernst-Planck theory with application to ion transport through the

gramicidin A channel. Biophys J 1999; 76: 789-791.

[36] Kuyucak S, Hoyles M, Chung SH. Analytical solution of Poisson equation for realistic

geometrical shapes of membrane ion channels. Biophys J 1998; 74: 22-36.

[37] Kuyucak S, Anderson OS, Chung SH. Models of permeation in ion channels. Rep Prog

Phys (2001); 64: 1427-1472.

[38] Kuyucak S, Chung SH. Permeation models and structure-function relationships in ion

channels. J Biol Phys 2002: 28: (289-308.

[39] Kuyucak S. Bustug T. Physics of ion channels. J Biol Phys 2003; 29: 429-446.

[40] Levitt D. General continuum theory for multiion channel. I. Theory. Biophys J 1991; 59:

271-277.

[41] Levitt D. Modelling of ion channels. J Gen Physiol 1999; 113: 789-794.

[42] LeMasurier M, Heginbotham L, Miller Ch. KcsA: It's a Potassium Channel. 2001: J Gen

Physiol 2001; 118: 303-313.

[43] Loughed T, Zhang Z, Wooley GA, Borisenko V. Enginneering charge selectivity in

model channels. Bioorg Med Chem 2004; 12: 1337-1342.

[44] Mamonov AB, Coalson RD, Nitzan A, Kurnikova MG. The role of the dielectric barrier

in narrow biological channels: A novel composite approach to modelling single-channel

currents. Biophys J 2003; 84: 3646-3661.

[45] Miller Ch. Ionic hopping defended. J Gen Physiol 1999: 113: 783-787.

[46] Miller Ch. Ion channels: doing hard chemistry with hard ions. Current Opinion in Chem

Biol 2000; 4: 148-151.

[47] Morais-Cabral JH, Zhou Y, MacKinnon R. Energetic optimization of ion conduction rate

by the K⁺ selectivity filter. Nature 2001; 414: 37-42.

[48] Moves H, Hodgkin-Huxley: Thirty years after. Current Topics in Membrane and

Transport 1984; 22: 279-329.

[49] Moy G, Corry B, Kuyucak S, Chung SH. Tests of continuum theories as models of ion

channels. I. Poisson-Boltzmann theory versus Brownian dynamics. Biophys J 2000; 78:

2349-2363.

[50] Murzyn K. Woda w symulacji dynamiki molekularnej. Postępy Biologii Komórki 2002;

29: 87-101.

[51] Nadler B. Mathematical models of ionic flow through open protein channels. Thesis for

the degree "Doctor of Philosophy", Tel Aviv University. 2002.

[52] Neher E, Sakmann B. Single-channel currents recorded from membrane of denervated

frog muscle fibres. Nature 1976; 260: 799-802.

[53] Nelson PH. A permeation theory for single-file ion channels: Corresponding occupancy

states produce Michaelis-Menten behavior. J Chem Phys 2002; 117: 11396-11403.

[54] Nelson PH. A permeation theory for single-file ion channels: Concerted-

association/dissociation. J Chem Phys 2003; 119: 6981-6982.

[55] Nelson PH. Modeling the concentration-dependent permeation modes of the KcsA

potasium channel. Phys Rev E 2003; 68: 061908.

[56] Nonner W, Eisenberg RS. Ion permeation and glutamate residues linked by Poisson-

Nernst-Planck theory in L-type calcium channels. Biophys J 1998; 75: 1287-1305.

[57] Nonner W, Chen DP, Eisenberg RS. Progress and prospect in permeation. J Gen

Physiol 1999; 113: 773-782.

[58] Oosting PH. Signal transmission in the nervous system. Rep Prog Phys 1979; 42: 1479-

1532.

[59] Roux B, Allen S, Berneche S, Im W. Theoretical and computational models of biological

ion channels. Q Rev Biophys 2004; 37: 15-103

[60] Sakmann B, Neher E. Single-channel recording. New York, Plenum Press 1995.

[61] Sansom MSP, Shrivastava IH, Bright JH, Tate Capener ChE, Biggin PC. Potasium

channels: structures, models, simulations. Biochim Biophys Acta 2002; 1565: 294-307.

[62] Schuss Z, Nadler B, Eisenberg RS. Derivation of Poisson and Nernst-Planck equation in

a bath and channel from a molecular model. Phys Rev E 2001; 64: 036116.

[63] Schutz CN, Warshel A. What are the dielectric "constants" of protein and how to validate

electrostatic models? Proteins 2001; 44: 400-417.

[64] Shrivastava IH, Sansom MSP. Simulation of ion permeation through a potassium

channel: molecular dynamics of KcsA in a phospholipid bilayer. Biophys J 2000; 78:

557-570.

[65] Sten-Knudsen O. Biological Membranes: Theory of transport, potentials and electric

impulses. Cambridge: Cambridge University Press 2002.

[66] Tieleman DP, Biggin PC, Smith GR, Sansom MSP. Simulation approaches to ion

channel structure-function relationships. Q Rev Biophys 2001; 34: 473-561.

[67] Tieleman DP, Borisenko V, Sansom MSP, Wooley GA. Understanding pH-dependent

selectivity of alamecithin K18 channels by computer simulation. Biophys J 2003; 84:

1464-1469.

[68] Weiss TF. Cellular Biophysics. Camnbridge, Massachusetts: A Bradford Book, The MIT

Press 1996.

[69] Yang KL, Yiacoumil S. Canonical Monte Carlo simulation of the fluctuacting-charge

molecular water between charged surfaces. J Chem Phys 2002; 117: 337-345.

[70] Yang KL, Yiacoumil S, Tsouris C. Monte Carlo simulation of electric double-layer

formation in nanopores. J Chem Phys 2002; 117: 8499-8507.

[71] Yellen G. The moving parts of voltage-gated ion channels. Q Rev Biophys 1998; 31: 239-

295.

[72] Yesylevskyy SO, Kharkyanen VN. Quasi-particles in the selectivity filter can explain

permeation in a channel with multiple occupancy. Phys Chem Chem Phys 2004; 6: 3111-

3122.

[73] Zhou Y, Morais-Cabral JH, Kaufman A, MacKinnon R. Chemistry of ion coordination

and hydration revealed by a K⁺ channel-Fab complex at 2,0 Ĺ resolution. Nature 2001;

414: 43-48.

20

---