Sprawozdanie z laboratorium z fizyki

Ćwiczenie nr 4

Temat ćwiczenia: Badanie siły tarcia.

Data wykonania ćwiczenia: 13.03.07.

Sekcja nr 4 w składzie:

1 Major Arleta

2 Marszałek Weronika

3 Zelga Klaudia

Data oddania sprawozdania (uzupełnia prowadzący): …

Ocena (uzupełnia prowadzący): …

I Wstęp teoretyczny.

Tarcie jest siłą, która przeciwstawia się ruchowi obiektów. Siła ta jest zawsze skierowana przeciwnie

do prędkości. Kiedy działamy na ciało siłą F, pojawiająca się siła tarcia fs skierowana w przeciwną stronę, która przeciwdziała ruchowi. W rezultacie ciało pozostaje w spoczynku. Siła tarcia ma jednak pewną wartość graniczną, zwaną siłą tarcia statycznego. Warunek pozostawania ciała w spoczynku możemy więc zapisać w postaci 0<F<fs Gdy zwiększa się wartość przykładanej siły, wartość siły fs także wzrasta, a gdy osiąga wartość

graniczną Jeżeli siła F będzie większa od fs ciało zacznie się poruszać ruchem jednostajnie przyspieszonym, ale przyspieszenie będzie jednak mniejsze niż w przypadku działania

tylko siły F, bowiem siła tarcia, zwana siłą tarcia kinetycznego fk będzie przeciwdziałać ruchowi. Zależności te

możemy zapisać następująco: Aby ciało poruszało się ruchem jednostajnym, zazwyczaj konieczne jest

zmniejszenie przykładanej siły Tarcie statyczne > Tarcie kinetyczne

Mechanizm tarcia

Źródłem tarcia statycznego są punktowe oddziaływania atomowe. Efekty dźwiękowe stowarzyszone z tarciem (np.

przy ostrym hamowaniu samochodu, otwieraniu drzwi z zardzewiałymi zawiasami) są związane ze skokowym

charakterem ruchu ślizgowego. Tarciu zawdzięczamy dźwięki skrzypiec.

Właściwości siły tarcia

Jeśli ciało się nie porusza, to siła tarcia statycznego fs oraz składowa siły F równoległa do powierzchni, równoważą się. Siły mają jednakową wartość, a fs jest przeciwnie skierowana do składowej równoległej siły F.

Maksymalna wartość siły fs - oznaczmy ją fs,max, dana jest wzorem: fs, max= msN, gdzie ms jest współczynnikiem tarcia statycznego, N - to wartość siły normalnej (działającej ze strony powierzchni). Jeśli ciało ślizga się po powierzchni, wartość tarcia maleje do wartości: fk = mkN, gdzie mk jest współczynnikiem tarcia kinetycznego. mk i ms są bezwymiarowe, zależą od właściwości ciała.

Tarcie na równi pochyłej

Ciało znajdujące się na równi pochyłej działa siłą ciężkości Q, której wektor skierowany jest prostopadle do podłoża. Rozłóżmy wektor siły Q na składowe:

- siła nacisku N, skierowana zawsze prostopadle do powierzchni równi

- siła powodująca zsuwanie ciała Fs, której wektor jest równoległy do powierzchni równi

Ponadto występują jeszcze siły FR- siła reakcji podłoża, która równoważy siłę nacisku N oraz siła tarcia - przeciwnie skierowana do siły Fs i równa jej jeżeli ciało nie zsuwa się z równi.

Kąt jaki tworzy ze sobą siła nacisku N i ciężar Q jest zawsze taki sam jak kąt nachylenia równi (ponieważ trójkąt xhl jest podobny do trójkąta NFsQ), więc dysponując ciężarem i kątem nachylenia równi pochyłej możemy wyliczyć każdą siłę. I tak:

sina=Fs/Q, czyli Fs=Qsina

cosa=N/Q, czyli N=Qcosa

Ponadto prawdziwe są proporcje:

N/Q=x/l

z twierdzenia Pitagorasa więc

oraz

Pozostaje nam jeszcze jedna siła- siła tarcia. Jeżeli ciało na równi pozostaje w spoczynku to siła tarcia jest równa sile zsuwania. Dzięki temu za pomocą równi możemy obliczać współczynniki tarcia statycznego. Aby to zrobić należy umieścić ciało na równi o jak największym kącie nachylenia, przy czym ciało nie może się przemieszczać! Wtedy Fs=Tmax (Tmax-maksymalna wartość tarcia statycznego), wiemy też, że:

Tmax=f0N, więc:

Fs=f0N, i tak otrzymujemy

f0=Fs/N

Korzystając z wcześniej wyprowadzonych wzorów otrzymujemy:

f0=Qsina/Qcosa, co po przekształceniu daje:

f0=tga

Tarcie przy toczeniu

Z doświadczenia wiemy, że podczas przetaczania ciężkiego walca po poziomej płaszczyźnie występuje opór, który

nazywamy oporem toczenia lub przez analogię do tarcia poślizgowego tarciem tocznym. Załóżmy, że sztywny walec o ciężarze G spoczywa na sztywnej poziomej płaszczyźnie. Do walca przyłożymy

poziomą siłę F odległą od płaszczyzny o h.

Dla każdej wartości siły F≠0 i h≠0 siła ta daje moment względem punktu A, którego wartość jest różna od zera: M=Fh≠0 W tej sytuacji najmniejsza siła F spowodowałaby obrót walca (toczenie), co jest sprzeczne z zachowaniem się ciał rzeczywistych w podobnej sytuacji. Zjawisko oporu toczenia jest spowodowane odkształcaniem się

zarówno walca, jak i płaszczyzny, na której on spoczywa - styk walca i płaszczyzny nie odbywa się wzdłuż tworzącej przechodzącej przez punkt A, lecz na ograniczonej powierzchni wynikającej ze wzajemnych odkształceń w miejscu styku walca i powierzchni.

Siła N jest więc wypadkową nacisków normalnych występujących na płaszczyźnie styku i działających na walec i jest przesunięta o pewną odległość w stosunku do punktu A w kierunku możliwego toczenia się. Aby równowaga walca była zachowana, moment siły F względem punktu A musi być zrównoważony momentem siły normalnej N względem tego punktu: Fh=M(N). Moment M(N) nie może wzrastać nieograniczenie, lecz tylko do pewnej

maksymalnej wartości. W przypadku granicznym jest on proporcjonalny do reakcji normalnej: Występujący w tym wzorze współczynnik proporcjonalności f nazywamy współczynnikiem tarcia tocznego albo ramieniem tarcia tocznego. Współczynnik ten ma wymiar długości i jest podawany w metrach.

II Przebieg ćwiczenia:

1. Opis wykonywanych czynności;

1. Tarcie kinetyczne i statyczne, badane na równi pochyłej

Siłę tarcia statycznego oraz kinetycznego badano na równi pochyłej z możliwością dynamicznej zmiany kąta.

By zbadać maksymalną siłę tarcia dla badanych obiektów, kładziono je na równi pochyłej z możliwością zmiany kąta nachylenia i powoli zwiększano kąt, do momentu ruszenia się ciała. Odczytana maksymalna wartość kąta daje obraz największej siły tarcia, jaka jest w stanie utrzymać ciało w bezruchu, mimo działających sił zewnętrznych.

Fs =
sFn

oraz

G cosα = Fn

G sinα =
sFn

Z tego otrzymujemy:

s = tg α_s

Jak widać aby otrzymać wartość współczynnika tarcia wystarczy zmierzyć wartość kąta α.

Następnie po wykonaniu tych czynności badano współczynnik tarcia kinetycznego. Po osiągnięciu maksymalnego wychylenia i ruszeniu się ciała, redukowano kąt tak, by ciało poruszało się ruchem jednostajnym prostoliniowym. Odczytana wartość była tak jak poprzednio informacją do obliczenia współczynnika tarcia.

_k = tg α_k

2. Tarcie toczne

Ćwiczenie wykonano podobnie jak przy wyznaczaniu współczynnika tarcia dla klocka

3. Pomiar sił tarcia przy toczeniu i ślizganiu

Do wyznaczenia siły tarcia przy toczeniu i ślizganiu posłużono się przyrządem:

W pierwszej kolejności badano siłomierzem, jaką siłę należy przyłożyć, by odkształcić sprężynę o długość l, gdy bloczek był odblokowany. Przeprowadzano po 6 pomiarów dla każdej z trzech długości sprężyny. Następnie przeprowadzano tę samą procedurę przy zablokowanym bloczku.

2. Tabele wyników

1. Badanie tarcia na równi pochyłej:

Numer pomiaru	materiał powierzchni równi	materiał powierzchni klocka	 s	 k	 s	 k
1	drewno	drewno	30	20	0,577	0,363
2					30	23	0,577	0,424
3					33	23	0,649	0,424
4					29	24	0,554	0,445
5					28	25	0,531	0,466
6					28	23	0,531	0,424
Średnia			29,67	23	0,57	0,42
Odchylenie standardowe			0,76	0,68	0,018	0,014
1	drewno	metal	28	19	0,531	0,344
2					26	21	0,487	0,383
3					28	18	0,531	0,324
4					24	19	0,445	0,344
5					27	18	0,509	0,325
6					25	22	0,466	0,404
Średnia			26,33	19,5	0,49	0,354
Odchylenie standardowe			0,66	0,67	0,014	0,013
1	drewno	guma	26	22	0,487	0,404
2					26	23	0,487	0,424
3					30	24	0,577	0,445
4					28	24	0,531	0,445
5					29	23	0,554	0,424
6					29	21	0,554	0,383
średnia			28	22,83	0,53	0,421
Odchylenie standardowe			0,68	0,48	0,015	0,01

Obliczanie odchylenia standardowego:

l.p.	 s - sr	( s - sr)^2		 k - sr	( k - sr)^2		 s - sr	( s - sr)^2		 k - sr	( k - sr)^2
1	0,33	0,11		-3	9		0,01	0,0001		-0,06	0,004
2	0,33	0,11		0	0		0,01	0,0001		0,00	0,000
3	3,33	11,11		0	0		0,08	0,0063		0,00	0,000
4	-0,67	0,44		1	1		-0,02	0,0003		0,02	0,000
5	-1,67	2,78		2	4		-0,04	0,0015		0,04	0,002
6	-1,67	2,78		0	0		-0,04	0,0015		0,00	0,000
Suma		17,33		0	14			0,0096			0,006
Odchylenie		0,76			0,68			0,018			0,014
1	1,67	2,78		-0,5	0,25		0,036	0,0013		-0,01	0,0001
2	-0,33	0,11		1,5	2,25		-0,008	0,0001		0,029	0,000841
3	1,67	2,78		-1,5	2,25		0,036	0,0013		-0,03	0,0009
4	-2,33	5,44		-0,5	0,25		-0,050	0,0025		-0,01	0,0001
5	0,67	0,44		-1,5	2,25		0,014	0,0002		-0,029	0,000841
6	-1,33	1,78		2,5	6,25		-0,029	0,0008		0,05	0,0025
Suma		13,33			13,5			0,0062			0,005282
Odchylenie		0,66			0,67			0,014			0,013
1	-2	4		-0,83	0,69		-0,04	0,0020		-0,017	0,000283
2	-2	4		0,17	0,03		-0,04	0,0020		0,0032	0,000009
3	2	4		1,17	1,36		0,05	0,0021		0,0242	0,000584
4	0	0		1,17	1,36		0,00	0,0000		0,0242	0,000584
5	1	1		0,17	0,03		0,02	0,0005		0,0032	0,000009
6	1	1		-1,83	3,36		0,02	0,0005		-0,038	0,001431
Suma		14			6,83			0,0070			0,002901
Odchylenie		0,68			0,48			0,015			0,01

b) Badanie tarcia na płaskim podłożu z użyciem siłomierza

Numer pomiaru	Materiał powierzchni podłoża	Materiał powierzchni klocka	masa klocka	Fd [N]	 k
1	drewno	drewno	142,3 g	0,45	0,32
2							0,5	0,35
3							0,4	0,29
4							0,6	0,43
5							0,55	0,39
6							0,45	0,32
Średnia				0,49	0,35
Odchylenie				0,03	0,02
1	drewno	guma	151,03 g	0,55	0,37
2							0,6	0,4
3							0,55	0,37
4							0,55	0,37
5							0,5	0,33
6							0,6	0,4
Średnia				0,56	0,37
Odchylenie				0,015	0,01
1	drewno	metal	183,54 g	0,6	0,33
2							0,6	0,33
3							0,65	0,36
4							0,7	0,39
5							0,6	0,33
6							0,55	0,31
Średnia				0,61	0,34
Odchylenie				0,021	0,012

Obliczanie odchylenia standardowego:

L.p	Fd - Fdsr.	(Fd -Fdsr.)^2		 k -sr	( k -sr)^2
1	-0,04	0,0017		-0,03	0,0009
2	0,01	0,0001		0,00	0,0000
3	-0,09	0,0084		-0,06	0,0036
4	0,11	0,0117		0,08	0,0064
5	0,06	0,0034		0,04	0,0016
6	-0,04	0,0017		-0,03	0,0009
Suma		0,0271			0,0134
Odchylenie		0,03			0,021
1	-0,01	0,0001		-0,00333	1,1E-05
2	0,04	0,0017		0,02667	0,00071
3	-0,01	0,0001		-0,00333	1,1E-05
4	-0,01	0,0001		-0,00333	1,1E-05
5	-0,06	0,0034		-0,04333	0,00188
6	0,04	0,0017		0,02667	0,00071
Suma		0,0071			0,00333
Odchylenie		0,015			0,01
1	-0,016666667	0,00027778		-0,01167	0,00014
2	-0,016666667	0,00027778		-0,01167	0,00014
3	0,033333333	0,00111111		0,01833	0,00034
4	0,083333333	0,00694444		0,04833	0,00234
5	-0,016666667	0,00027778		-0,01167	0,00014
6	-0,066666667	0,00444444		-0,03167	0,001
Suma		0,01333333			0,00408
Odchylenie		0,021			0,012

c) Badanie tarcia przy toczeniu się walca:

Numer pomiaru	Promień podstawy walca	 g	 
1	15 mm	8	0,0021
2			7,5	0,00197
3			7	0,00184
4			8	0,0021
5			7,5	0,00197
6			8	0,0021
Średnia		7,67	0,0020
Odchylenie		0,17	0,00011
1	11mm	6	0,00115
2			6	0,00115
3			7	0,00135
4			7	0,00135
5			6,5	0,00125
6			6,5	0,00125
Średnia		6,5	0,00125
Odchylenie		0,18	0,00004
1	7,5 mm	7	0,00092
2			7,5	0,00099
3			7	0,00092
4			7,5	0,00099
5			8	0,00105
6			7,5	0,00099
Średnia		7,42	0,00098
Odchylenie		0,15	0

Obliczanie odchylenia standardowego:

L.p.	 g - sr	( g - sr)^2		   sr	(   sr)^2
1	0,33	0,11		0,00009	0,00000
2	-0,17	0,03		-0,00004	0,00000
3	-0,67	0,44		-0,00017	0,00000
4	0,33	0,11		0,00009	0,00000
5	-0,17	0,03		-0,00004	0,00000
6	0,33	0,11		0,00009	0,00000
Suma		0,83			0,00000
Odchylenie		0,17			0
1	-0,5	0,25		-0,0001	0,0000001
2	-0,5	0,25		-0,0001	0,0000001
3	0,5	0,25		0,0001	0,0000001
4	0,5	0,25		0,0001	0,0000001
5	0	0		0	0
6	0	0		0	0
Suma		1			0,0000004
Odchylenie		0,18			0,00004
1	-0,42	0,17		-0,00006	0,00000
2	0,08	0,01		0,00001	0,00000
3	-0,42	0,17		-0,00006	0,00000
4	0,08	0,01		0,00001	0,00000
5	0,58	0,34		0,00007	0,00000
6	0,08	0,01		0,00001	0,00000
Suma		0,71			0
Odchylenie		0,15			0

d) Badanie siły tarcia przy ślizganiu i toczeniu:

Numer pomiaru	Rozciągnięcie sprężyny	Ślizganie	Toczenie	Stosunek sił F1/F2
1	1 mm	0,55	0,2	2,75
2			0,6	0,25	2,4
3			0,7	0,15	4,67
4			0,7	0,2	3,5
5			0,65	0,2	3,25
6			0,7	0,25	2,8
Średnia		0,65	0,208	3,23
Odchylenie		0,063	0,038	0,805
1	5 mm	3	1	3
2			2,5	1,5	1,67
3			2,7	0,9	3
4			3	1	3
5			3,2	0,85	3,76
6			3,3	1	3,3
Średnia		2,95	1,04	2,96
Odchylenie		0,30	0,23	0,70
1	10 mm	7	2	3,5
2			6,5	2,5	2,6
3			7	2,4	2,92
4			6,5	2,3	2,83
5			7	2	3,5
6			7	2,5	2,8
Średnia		6,83	2,28	3,02
Odchylenie		0,26	0,23	0,38

3. Wyniki;

• dla klocka z gumową płytką.

α_{s śr}=28°± 0,68° μ_s=0,53±0,015

α_{k śr}=22,83°± 0,01° μ_k=0,42±0,01

• dla klocka z metalową płytką.

α_{s śr}=26,33°± 0,66° μ_s =0,49±0,014

α_{k śr}=19,5°±0,67° μ_k =0,35 ±0,013

• dla drewnianego klocka

α_{s śr}=29,67°±0,76° μ_s =0,57±0,018

α_{k śr}=23°±0,68° μ_k =0,42±0,014

• dla klocka z gumową płytką m=151,03 g

F_d=0,56± 0,015[N] μ_k=0,37±0,01

• dla klocka z metalową płytką m=183,54 g

F_d=0,61± 0,021[N] μ_k=0,34±0,012

• dla drewnianego klocka o m= 142,3 g

F_d=0,49± 0,03[N] μ_k=0,35±0,02

• dla walca o r=15 mm

α_{g śr}=7,67°± 0,17° μ_T=0,002±0,0001

• dla walca o r=11 mm

α_{g śr}=6,5°± 0,18° μ_T0,00125±0,00004

• dla walca o r=7,5 mm

α_{g śr}=7,42°±0,15° μ_T=0,00098±0

● dla rozciągnięcia sprężyny 1 mm

F1=0,65±0,063 F2=0,208±0,038 F1/F2=3,23±0,805

● dla rozciągnięcia sprężyny 5 mm

F1=2,95±0,3 F2=1,04±0,23 F1/F2=2,96±0,7

● dla rozciągnięcia sprężyny 10 mm

F1=6,83±0,26 F2=2,28±0,23 F1/F2=3,02±0,38

4.Analiza błędów:

Wszystkie błędy obliczano ze wzoru na odchylenie standardowe:

S=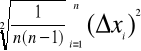

4. Analiza błędów.

III Wnioski.

Pierwsza część pomiaru, dotycząca badania tarcia statycznego i kinetycznego na równi pochyłej obarczona jest, pewnikiem, sporym błędem. Wpłynęło na ten stan rzeczy szereg czynników, między innymi: mierzenie kąta nachylenia równi, gdzie niepopełnie błędu było nie możliwe ze względu na odczytywanie wartości kąta „na oko”. Innym, równie ważnym czynnikiem były nierówności i różne współczynniki tarcia na różnych odcinkach równi. Niejednolite współczynniki zostały zauważone przy wykonywaniu ćwiczenia z dynamometrem, który wykazał inną wartość na początkowym odcinku deski, a inną na końcowym odcinku. Przyczyną było wytarcie materiału przez użytkowników, którzy w większości wykonywali eksperymenty na końcowym odcinku równi. Bład pomiaru wskazuje jednoznacznie na spore odchylenia, jego małe wartości są złudne, gdyż wartości współczynników tarcia oscylują w granicach jedności i w praktyce minimalna zmiana znacząco wpływa na wartość siły.

W przypadku dwóch klocków: z gumową oraz z metalową płytką współczynniki tarcia wyliczone z kątów nachylenia równi są znacznie większe od współczynników wyliczonych ze wskazań dynamometru. Ciężko jest stwierdzić, co mogło być tego przyczyną, obserwując jednak pozostałe wyniki dochodzi się do wniosku, że ogólnie zawsze wyniki z obliczeń tgα są większe od wyników z F. Można tylko przypuszczać, że wzięto zły punkt odniesienia na desce do sczytywania kąta, lub też (co mniej prawdopodobne) siłomierz wskazywał błędne wartości.

Co do tarcia tocznego również decydującym czynnikiem prawidłowości wyników był odczyt kąta. Było to tym trudniejsze, że wartości były bardzo niskie i ciężko było zauważyć różnicę kątów dla kolejnych walców. Tutaj błąd jest olbrzymi w stosunku do wyników, a tym samym potwierdza założenia podane wyżej.

Pomiar sił tarcia przy toczeniu i ślizganiu został obarczony również sporym błędem, gdyż sprężyna, dla której wychylenia badano siły, ulegała częstokroć rozciągnięciom, co w efekcie fałszowało wyniki. Również w tym przypadku niedokładność polegała na odczycie wyników siłomierza, jak również ustaleniu jednakowych wychyleń sprężyny dla wykonywanych prób. Obserwując jednak wyniki, okazało się, że stosunki są dość do siebie zbliżone, a więc próby można przyjąć za wiarygodne.

W tym ćwiczeniu potwierdzono:

• że maksymalna wartość współczynnika tarcia statycznego jest zawsze większa od współczynnika tarcia kinetycznego

• że współczynnik tarcia tocznego jest taki sam (w przybliżeniu) dla ciała w spoczynku jak i w ruchu

• że współczynnik tarcia zależy od rodzaju powierzchni sykających się ciał

Podsumowanie z życia wzięte:

Tarcie statyczne jest siłą, która przyjmuje największe wartości spośród wszystkich rodzajów tarcia. Ruszenie ciała z miejsca wymaga zdecydowanie większej siły niż utrzymanie tego samego ciała w ruchu. Ta dysproporcja w siłach potrafi być częstokroć frustrująca, chociażby przy przesuwaniu szafy po panelach podłogowych. Żeby ruszyć ją z miejsca, potrzebna jest spora siła i człowiek w skarpetkach nie jest w stanie jej przezwyciężyć, gdyż współczynnik tarcia na lini skarpeta - podłoga jest zbyt mały i mniejszy od współczynnika tarcia statycznego szafa - podłoga. Przez dysproporcję pomiędzy współczynnikiem tarcia statycznego i dynamicznego człowiek przy poślizgu może się nawet wywrócić, gdyż mięśnie działając tą samą siłą przy tarciu kinetycznym w poślizgu, będą wprawiały nogi w ruch jednostajnie przyspieszony. Jedynym sposobem by przesunąć szafę po podłodze jest zdjęcie skarpet, i dzięki szeregowi czynników, które występują na gołej stopie (wilgotność skóry, liniom papilarnym etc.) jesteśmy w stanie przezwyciężyć siłę tarcia statycznego i przesunąć szafę w pożądane miejsce.

(autor w trakcie pisania sprawozdania)

-Fn

x

F_s

α

Gsinα

α

Gcosα

G

y

sprężyna

dynamometr

F

---