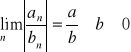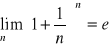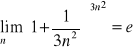Logika, wielomiany z dwumianu Newtona, macierze, liczby zespolone (potęga, pierwiastek), granice ciągu. 6 zadań.

Ciągi i ich granice.

Ciągiem liczbowym niekończącym nazywamy zbiór w postaci
lub
lub
, gdzie n = 1, 2, 3, ... przy czym
są liczbami, które ustawiono w pewnym ściśle określonym przypadku.

Ciąg skończony.

Ciągiem skończonym k-wyrazowym, nazywamy skończony zbiór elementów, przy czym każdej liczby naturalnej 1-k została przyporządkowana pewna liczba.

Ciąg może być określony wzorem ogólnym, regulacyjnym, wykresem, tabelą lub przepisem słownym.

Monotoniczność ciągu.

Ciąg może być rosnący.

1. Ciąg rosnący:
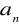
   jest rosnący wtedy i tylko wtedy, gdy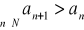
   .

2. Ciąg malejący:
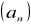
   jest malejący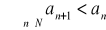
   .

3. Ciąg niemalejący:
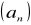
   jest niemalejący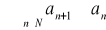
   .

4. Ciąg nierosnący:
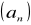
   jest nierosnący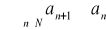
   .

Przykład.

1. 
   
   
   
   Wykaż, że ciąg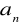
   w wyrazie ogólnym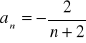
   jest ciągiem rosnącym.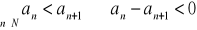
   
   !
   
   

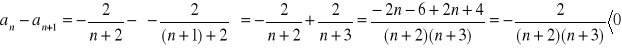
2. 
   
   
   Zbadaj monotoniczność ciągu (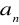
   ) o wyrazie ogólnym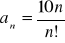
   .
   
   
   
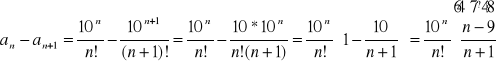
   1.
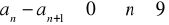
   dla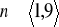
   - ciąg jest niemalejący.
   2.
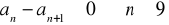
   dla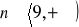
   - ciąg jest nierosnący.

Granice ciągu.

Granica ciągu nieskończonego
, przy n dążącym do nieskończoności jest liczba „g”, wtedy i tylko wtedy, gdy dla każdej dodatniej liczby „
” istnieje takie „
”, że dla „n” większego od „
” wartość bezwzględna różnicy n-tego wyrazu ciągu i granicy „g” jest mniejsza od „
”.

TWIERDZENIA!

1. Każdy ciąg monotoniczny i ograniczony jest zbieżny.
   Ciąg jest ograniczony z dołu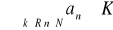
   .
   Ciąg jest ograniczony z góry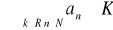
   .
   Ciąg jest ograniczony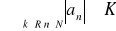
   .

2. Jeżeli ciąg jest zbieżny to jest ograniczony.

WZORY:

1. 
   
   

2. 
   
   

3. 
   

4. 
   

5. 
   

6. 
   
   
   
   

7. 
   
   
   

8. 
   
   

9. 
   
   

10. 
    
    

11. 
    
    
    

12. 
    

Symbole nieoznaczone.

Przykłady:

1. 
   
   
   
   
   
   
   
   
   
   
   
   
   Oblicz granicę ciągu.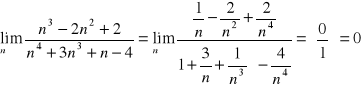
   
   
   
   
   

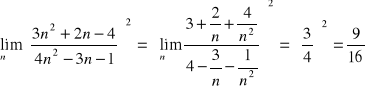
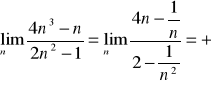
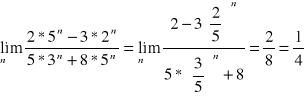
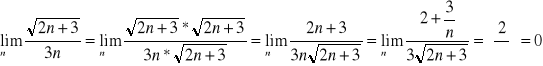
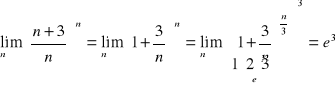
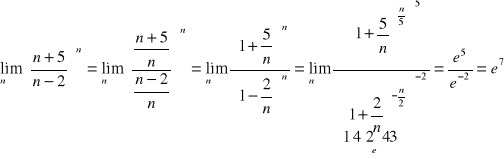
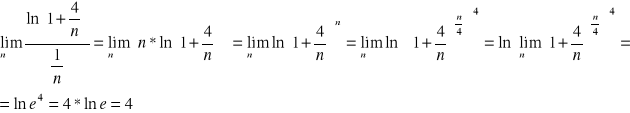
2. 
   
   
   
   
   
   
   

3. 
   
   
   
   
   
   
   
   

4. 
   
   
   
   

5. 
   
   
   
   
   
   

6. 
   
   

7. 
   
   

8. 
   

Twierdzenie o 3 ciągach.

Jeżeli
i jeżeli istnieje liczba „
” taka, że dla każdej liczby naturalnej
, spełniona jest nierówność
to
.

Przykład.

Oblicz
.

Ponieważ
, to na podstawie twierdzenia o 3 ciągach to wyjściowa granica
.

Ciąg arytmetyczny.

Ciąg nazywamy ciągiem arytmetycznym

Monotoniczność ciągu zależy od różnicy ciągu „r”:

1. 
   ciąg rosnący

2. 
   ciąg malejący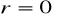

3. 
   ciąg stały

Ciąg geometryczny.

Ciągiem geometrycznym nazywamy dany ciąg
.

Zadanie 1.

Ojciec miał 5 synów, którzy przychodzili na świat w 3 lata, począwszy od ich 5 roku życia ojciec dawał każdemu z synów na urodziny tyle książek ile każdy miał lat. Ile lat miał każdy z synów, gdy łącznie otrzymali od ojca 450 książek.

Ciąg rosnący

> 0

> 0

> 0

> 0

Ciągi
i
mają granice właściwe odpowiednio „a” i „b”.

Podstawa logarytmu podstawowego.

!

!

!

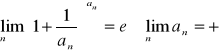
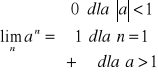
0

0

0

0

0

0

1

0

0

0

0

0

0

0

1

!

!

dla

1 syn - n-lat

2 syn - n + 3 lat

3 syn - n + 6 lat

4 syn - n + 9 lat

5 syn - n + 12 lat

Dostali książki po:
ilość elementów ciągu.

sprzeczne

---