Politechnika Poznańska Wydział Elektryczny	Laboratorium Metrologii Elektrycznej i Elektronicznej	Rok akademicki 2003/2004
Kierunek: Elektrotechnika Rok studiów: II Semestr: III	Temat: Pomiar rezystancji mostkiem Wheatstone'a
Wykonujący ćwiczenie: 1. Matelski Szymon 2. Matuszak Paweł 3. Melonek Andrzej	Data wykonania ćwiczenia: 07.11.2003	Zaliczenie:

Wiadomości wstępne.

Mostek Wheatstone'a. Jedno z ramion mostka zawiera mierzoną rezystancję, pozostałe zawierają rezystancje wzorcowe. Mostek jest zasilany ze źródła o rezystancji wewnętrznej R_W i napięciu źródłowym U. W przekątnej znajduje się galwanometr o rezystancji wewnętrznej R₀. W wykonywanym ćwiczeniu używany był miernik cyfrowy .

Warunek równowagi mostka: napięcie na galwanometrze jest równe zero. Ma to miejsce wtedy, gdy wartości prądów I₁=I₂ oraz I₃=I₄, co daje równości napięć na gałęziach mostka: I₁*R_X = I₃*R₃ oraz I₂*R₂ = I₄*R₄. Z tych zależności otrzymujemy

R_X * R₄ = R₂ * R₃

A zatem możemy wyznaczyć Rx.

Sa dwie metody równoważenia mostka:

- zmieniając wartość R2 przy stałym stosunku R3/R4, co w przypadku R3/R4 =10ⁿ pozwala na bezpośrednie odczytanie wartości Rx z nastawy R2 ( po uwzględnieniu przecinka).

- zmieniając stosunek R3/R4 przy stałej wartości R2 (stosowane w mostkach technicznych o malej dokładności).

Obliczenia

Dokonujemy pomiaru rezystancji R_x multimetrem cyfrowym, a następnie obliczamy błąd bezwzględny i względny pomiaru :

R_X = 510,4 Ω

Δ_X = 0,15% rdg + 3dgt = 1,1 Ω

Mierzymy rezystancję R_x przy pomocy mostka technicznego, przy którym błąd pomiaru wynosi δ_X = 1%

R_X = 510 Ω Δ_X = 1% R_X = 5,1 Ω

Zestawienie wyników pomiaru omomierze i mostkiem:

Rx [Ω]	[Ω]	Uwagi
510,4	± 1,1	Omomierz
510,0	± 5,1	Mostek techniczny

Wyznaczamy rezystancje R₂, R₃, R₄ :

= 0,02%

Z warunku równowagi mostka
wnioskujmy że
i przyjmujemy :

Określamy górną graniczną wartość napięcia zasilającego ze względu na dopuszczalną wartość obciążenia rezystorów w poszczególnych gałęziach :

Dla gałęzi górnej zawierająca rezystancje R_x i R₂ dopuszczalna moc P_max = 0,25 W

P_X = R I ²

I=

Natomiast dopuszczalny prąd dla rezystancji R₂ wynosi 30 mA .

Do wyznaczenia dopuszczalnego napięcia na gałęzi musimy podstawić najmniejszy dopuszczalny prąd tj. I=22 mA, wobec tego :

U_dop.= I_X ( R_X + R₃ ) = 22 V

Gałąź dolna zawierająca R₃ i R₄:

U_dop.= I₃ ( R₃ + R₄ ) = 2,22 ( 5000 + 5000 ) = 22,2 V

Napięcie źródła wynosiło 3 V więc nie przekraczało wartości dopuszczalnych.

Pomiary

Wykonujemy trzy pomiary rezystancji metodą interpolacji.

Do obliczenia interpolacji wykorzystujemy poniższy wzór:

pomiar	R2 [Ω]	α1 [div]	α2 [div]	ΔR2 [Ω]	R2i [Ω]
1	510,4	4	2	0,1	510,47
2	510,4	3	2	0,1	510,45
3	510,4	2	1	0,1	510,46

2.5.Zestawienie wyników

L.p.	R2 [Ω]	R3 [Ω]	R4 [Ω]	Rx [Ω]	δpR2 [%]	Uwagi
1	510,47	5000	5000	510,47	0,24	Mostek laboratoryjny UAB = 3 [mV] = 0,1 [Ω] = 0,1 [Ω]
2	510,45	5000	5000	510,45	0,24
3	510,46	5000	5000	510,46	0,24

Wartość średnia R_x:

Obliczamy całkowity błąd pomiaru :

Błędu spowodowanego wpływem siły termoelektrycznej nie uwzględniamy, więc

gdzie :

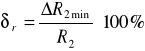
= 0,02 %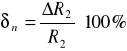
= 0,02 %

Jako że błędy te są sobie równe to do obliczeń przyjmujemy jeden z nich

Natomiast
obliczyliśmy już wcześniej i wynosi on

wobec tego całkowity błąd to:

błąd bezwzględny :

Ostatecznie, wartość R_x wynosi :

R_X = ( 510,46 ± 1,23 ) [Ω]

(wyniku nie zaokrąglam, by odzwierciedlić dokładność pomiaru wynikającą z zastosowania interpolacji)

Wnioski

Po wykonaniu powyższego ćwiczenia można stwierdzić, że pomiar rezystancji mostkiem laboratoryjnym Wheatstone'a jest pomiarem bardzo dokładnym. Błąd przy pomiarze tą metodą wynosi 0,24% co jest wartością bardzo niską. Dodatkowo zastosowanie metody interpolacji zwiększa dokładność pomiaru o jedno miejsce po przecinku.

---