DYNAMIKA

Znajdowanie ruchów na podstawie znajomości przyczyn  sił.

Siły są wektorami, jednostka siły w układzie SI - niuton [N]

Zasady dynamiki (prawa Newtona XVII w.)

1. Jeżeli na ciało nie działają siły lub działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ze stałą prędkością po linii prostej.

.

Jest to zasada bezwładności, znana już Galileuszowi - określa tzw. układy inercjalne. Ziemia jako układ prawie inercjalny (w  stopniu zależnym od skali ruchu i prędkości).

Układ związany z gwiazdami stałymi (zasada Macha).

2. Przyspieszenie ciała jest proporcjonalne do wypadkowej siły działającej na ciało a odwrotnie proporcjonalne do masy ciała. Przyspieszenie to ma kierunek i zwrot wypadkowej siły.

. (1)

Zasada spełniona w układach inercjalnych. Równanie (1) jest prawem wektorowym, zatem dla składowych siły :

F_x = m a_x, F_y = m a_y, F_z = m a_z

Zastosowanie dla ciał o stałej masie.

Przekształcamy równanie (1)

,
,
,
,

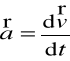
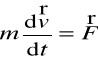
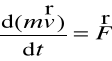
Określamy pęd
ciała o masie m i prędkości

.

Ogólna postać II zasady dynamiki

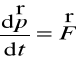
. (2)

Równanie Newtona (2) pozwala wyznaczyć siłę gdy znane są skutki jej działania. Jest ogólniejsze niż postać
, gdyż może być stosowane dla ciał o zmiennej masie np. rakiety.

Różniczkowe równania ruchu (drugiego rzędu):

,
,
.

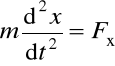
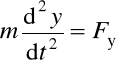
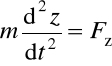
Problem polega na znalezieniu funkcji opisujących współrzędne ciała: x = f₁(t), y = f₂(t), z = f₃(t). Po wyeliminowaniu czasu - wyznaczenie toru ruchu (trajektorii).

3. Jeżeli ciało A działa na ciało B pewną siłą, to ciało B działa na  ciało A siłą równej wartości, ale skierowaną przeciwnie.

Wektory obu sił leżą na jednej prostej.

.

Zasada akcji i reakcji. Oba oddziaływania w tej samej chwili. Zasady Newtona stosują się do ciał, które można traktować jak  punkty materialne.

Każde ciało można uważać za układ punktów materialnych.

Zasady Newtona uogólniamy na układy punktów materialnych.

Ruch środka masy

Układ n punktów materialnych o masach m₁, m₂, m₃,....., m_n

Masa m_i ma prędkość
i przyspieszenie
.

Siła działająca na i-tą masę
,

gdzie:
- siła od masy m₁,
- siła od masy m₂, ,.......,
,........ ,
- siła od masy m_n,

- wypadkowa sił zewnętrznych działających na i-tą masę.

Zapisujemy układ równań wyrażających II zasadę dynamiki dla poszczególnych ciał:

(3)

.........................................................................

.........................................................................

Lewe strony układu równań (3) piszemy w postaci

.

Przekształcone równania (3) sumujemy stronami.

Suma lewych stron

=

=
.

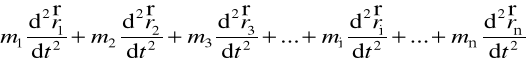
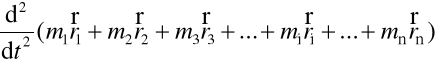
Ponieważ dla każdej pary sił
(3. zasada), więc suma sił wewnętrznych = 0, zatem suma prawych stron

gdzie
- suma wszystkich sił zewnętrznych (wektorowa!)

Oznaczamy

M_C = m₁ + m₂ + m₃ + ... + m_n - całkowita masa układu

.

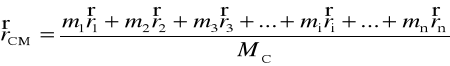
Suma lewych stron układu (3) = sumie prawych stron =
.

Z równości powyższej wynika równanie

. (4)

Formalnie równanie (4) opisuje ruch punktu materialnego o  masie  M_C pod   wpływem siły
.

Jest to równanie ruchu dla tzw. środka masy układu. Wektor wodzący środka masy dany jest wyrażeniem
. Przyspieszenie tego punktu wynosi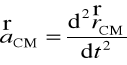
.

Zastosowanie - wyznaczanie ruchów układów wielu ciał.

Można rozdzielić ruchu środka masy układu i ruch obrotowy względem środka masy (szczególnie dla brył).

Zasada zachowania pędu

Wprowadzamy całkowity pęd układu:

gdzie
- pęd masy m_i.

Lewe strony układu równań (3) piszemy w postaci

.

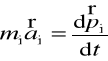
Sumujemy stronami równania (3) w powyższej postaci i otrzymujemy równanie

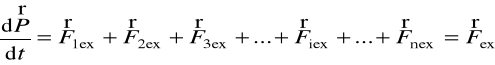
. (5)

Z równania (5) wynika zasada zachowania pędu

Jeżeli suma sił zewnętrznych jest zerowa to pęd jest stały. Zatem:

= 0

= const . (6)

Jeżeli któraś ze składowych sumy sił zewnętrznych jest zerowa to  odpowiednia składowa pędu nie zmienia się np.:

F_exx = 0
P_x = const.

Równanie (5) można przybliżyć dla skończonych przyrostów:

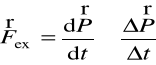
czyli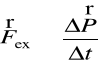
. (5' )

Przybliżenie (5') służy często do wyznaczania średnich sił

.

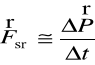
Zapisujemy (5' ) w postaci
. Stąd wynika wniosek:

jeżeli siły zewnętrzne nie są zbyt wielkie i działają bardzo krótko to można przyjąć, że
(zderzenia, rzuty).

Zasada zachowania pędu pozwala często obliczyć końcowe prędkości bez rozwiązywania skomplikowanych równań, wynikających z II zasady dynamiki.

Przykłady sił: naprężenia, reakcje, tarcie, siły sprężyste, ciężar, siły elektryczne, siły magnetyczne.

Tarcie

1. Tarcie statyczne.

Tarcie statyczne to opór ciała i podłoża przy próbie wprawiania ciała w ruch.

- siła próbująca poruszyć ciało,
- siła tarcia,

- nacisk normalny (prostopadły do podłoża).

Prawo tarcia statycznego: Siła tarcia zależy od rodzaju stykających się powierzchni, nie zależy od pola powierzchni trącej, jest skierowana przeciwnie do siły wprawiającej i nie

przekracza wartości określonej równaniem

T_max = μ_s N_n (7)

gdzie μ_s - współczynnik tarcia statycznego.

Jeżeli F < T_max to T = F i T < T_max

Ogólnie T ≤ μ_s N_n.

Tarcie statyczne bywa też nazywane tarciem spoczynkowym.

Gdy zewnętrzna siła poruszająca F przekroczy wartość T_max, wtedy tarcie zmienia charakter.

2. Tarcie kinetyczne

Tarcie kinetyczne to opór ciała i podłoża w czasie ruchu.

Prawo tarcia kinetycznego: Siła tarcia zależy od rodzaju stykających się powierzchni, nie zależy od prędkości i pola powierzchni trącej, jest skierowana przeciwnie do kierunku ruchu

i ma wartość określoną równaniem:

T = μ_k N_n , (8)

gdzie μ_k - współczynnik tarcia kinetycznego.

Z licznych doświadczeń T_kin < T_max stąd μ_k < μ_s .

Prawa sił tarcia są bardzo przybliżone. Dotyczą typowych powierzchni suchych, nie poddanych szlifowaniu ani też smarowaniu. Znał te prawa już Leonardo da Vinci (XV-XVI w).

Zależność siły tarcia T od siły F wyprowadzającej ciało ze spoczynku i wprawiającej je w ruch.

Siła dośrodkowa

Ruch po okręgu wymaga istnienia siły dośrodkowej :

(9)

W charakterze siły dośrodkowej mogą wystąpić różne rodzaje sił : reakcja podłoża, naprężenie linek i prętów, siła tarcia statycznego, siła ciężkości (ciała na Ziemi, satelity), siła elektrostatyczna (np. w atomach), siła magnetyczna (akceleratory cząstek).

Siła dośrodkowa
jest wypadkową sił mających składowe na kierunek promienia okręgu będącego torem ruchu ciała.

Pisząc równanie (9) bierzemy ze znakiem „+” siły (lub ich składowe) zwrócone do środka okręgu, a ze  znakiem „-” zwrócone od środka okręgu.

Siły bezwładności

Zasady dynamiki są słuszne w układach inercjalnych. Układy mające przyspieszenie nie są inercjalne.

Zakładamy, że cały układ ma tę samą prędkość (chwilową).

Z zasady składania ruchów wynika prędkość wypadkowa

,

zatem także przyspieszenie wypadkowe

.

Wskaźnik „ef” oznacza wartości efektywne czyli wypadkowe w układzie inercjalnym.

• Jeżeli
= const to
= 0 więc

Dla krótkości oznacza się zwykle
, czyli dla przyspieszenia określanego względem układu :

• Jeżeli

const to

0 więc :

.

Ponieważ
zatem :

.

Wielkość
jest tzw. siłą bezwładności

W układzie nieinercjalnym należy stosować II zasadę dynamiki w postaci uwzględniającej siły bezwładności

. (9)

Przykładem siły bezwładności jest siła odśrodkowa :

.

Doznaje jej działania obserwator w układzie poruszającym się po okręgu (np. na karuzeli) lub łuku okręgu (np. na zakręcie).

Inne przykłady: siły doznawane przez pasażerów podczas raptownego przyspieszania lub hamowania.

przyspieszanie

hamowanie

Ciężar. Grawitacja

W pobliżu powierzchni Ziemi ciała swobodnie spadają ze stałym przyspieszeniem g = 9,81m/s² (średnia wartość przyspieszenia ziemskiego na obszarze Polski). Działa siła
, czyli ciężar. Ogólnie wartość siły ciężkości, czyli grawitacji dana jest prawem Newtona (prawo powszechnego ciążenia):

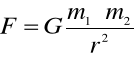
(10)

G = 6,67·10^11 N·m²/kg²  stała grawitacji.

Prawo dotyczy wzajemnego przyciągania punktowych mas m₁ i m₂ odległych o r. Siła działa wzdłuż prostej łączącej te masy.

Prawo jest ścisłe także dla jednorodnych kul, których środki odległe są o r (ciała niebieskie), a także oddziaływania kuli z niewielką masą (np. Ziemi z człowiekiem)

Jeżeli m₁ = M - masa Ziemi, r = R_z - promień Ziemi a m₂ = m - niewielka masa w pobliżu powierzchni Ziemi, to

.

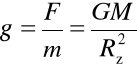
Przyspieszenie jest różne w różnych miejscach na Ziemi z powodu jej niekulistości i spłaszczenia.

Definiuje się tzw. normalne przyspieszenie ziemskie na poziomie morza i na szerokości geograficznej φ = 45°: g_n = 9,80665 m/s².

Grawitacja w teorii pola

Każde ciało jest źródłem pola grawitacyjnego. Rozpatrujemy źródło w postaci kuli o masie M (np. planetę). Umieszczamy początek układu współrzędnych w środku kuli. Masa M działa na punktowe ciało o masie m siłą

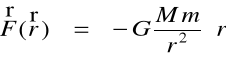
(11)

r - odległość od środka źródła do masy m,

- jednostkowy wektor od środka źródła do masy m.

Natężeniem pola grawitacyjnego źródła nazywamy wektor

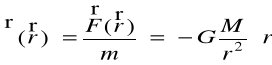
. (12)

Jeżeli na masę m działa jedynie siła grawitacji
, to zgodnie z II zasadą dynamiki nadaje tej masie przyspieszenie grawitacyjne

.

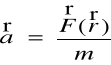
Wektor natężenia pola grawitacyjnego jest zatem równy wektorowi przyspieszenia grawitacyjnego. Wektory te opisują jednak różne własności:

- wektor
jest siłową charakterystyką źródła pola grawitacyjnego

- wektor
opisuje ruch w polu grawitacyjnym.

Ogólnie termin „pole grawitacyjne” oznacza funkcję przyporządkowującą punktowi w określonym obszarze przestrzeni, wskazywanemu przez wektor wodzący
pewną wielkość charakteryzującą oddziaływanie grawitacyjne, np. wektor  natężenia pola
.

T

T_max = μ_s N_n

T_kin = μ_k N_n

T = F

F

m

m

M

m

---