Aby określić, czy między zmiennymi występuje związek liniowy badam zależność korelacyjną między tymi zmiennymi.

Tworzę korelacyjny wykres rozrzutu:

Na podstawie wykresu możemy powiedzieć, ze miedzy przeciętnymi miesięcznymi dochodami mierzonymi w tyś. zł na osobę a średnimi tygodniowymi wydatkami w danym roku na słodycze występuje zależność liniowa.

Korelacja ta jest dość silna liniowo dodatnia, gdyż ze wzrostem jednej wartości rośnie i druga.

Aby zbadać sile i kierunek korelacji miedzy cechami: przeciętnymi miesięcznymi dochodami i średnimi tygodniowymi wydatkami w roku na słodycze posłużymy się współczynnikiem korelacji Pearlsona

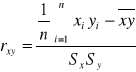
X- cecha niezależna - przeciętne miesięczne dochody w tyś. zł na osobę

Y- cecha zależna - średnie tygodniowe wydatki na słodycze w danym roku w zł.

Musze obliczyć wiec
( obliczenia zamieszczam w tabelce pomocniczej)

Następnie znajduje średnie arytmetyczne cechy X i Y oraz odchylenia standardowe dla każdej cechy:

=

=

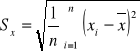
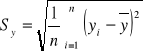
Przeciętne miesięczne dochody w tyś. zł na osobę.	Śr. tygodniowe wydatki w danym roku na słodycze w zł.
1,0	18	18	-1,3	1,69	-7,3	53,29
1,0	21	21	-1,3	1,69	-4,3	18,49
1,5	22	33	-0,8	0,64	-3,3	10,89
1,5	22	33	-0,8	0,64	-3,3	10,89
2,0	24	48	-0,3	0,09	-1,3	1,69
2,0	25	50	-0,3	0,09	-0,3	0,09
2,5	26	65	0,2	0,04	0,7	0,49
2,5	26	65	0,2	0,04	0,7	0,49
3,0	29	87	0,7	0,49	3,7	13,69
3,5	30	105	1,2	1,44	4,7	22,09
3,5	30	105	1,2	1,44	4,7	22,09
4,0	31	124	1,7	2,89	5,7	32,49
28	304	754		11,18		186,68

Suma

=
=
tyś. zł

=
=
zł na tydzień

=

=

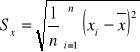
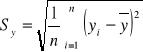
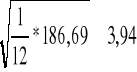
podstawiając wyliczone wartości do równania otrzymuje:

=

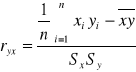
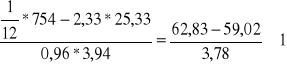
Ponieważ policzony wyżej współczynnik większy jest od 0,między zmiennymi x i y zachodzi korelacja dodatnia (wraz ze wzrostem wariantów jednej cechy- w tym przypadku przeciętnego miesięcznego dochodu , rosną warianty drugiej cechy, czyli średnie miesięczny wydatki na słodycze).

Wartość współczynnika przyjmująca wartość 1 wskazuje na zależność w postaci funkcji liniowej.

Aby oszacować parametry strukturalne modelu muszę zastosować MNK

ustalam postać macierzy X oraz wektora Y, która ma postać:

X=

Y=

=


=

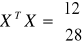
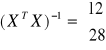
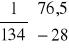
teraz obliczam

=

podstawiam do wzoru na estymatory MNK otrzymując:

=


=
=

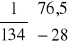
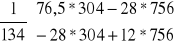
otrzymaliśmy wektor określający oszacowane parametry α
i α₁

α
=15,6

α₁ = 4,2

oszacowana postać modelu:

Parametr α
=16 jest wyrazem wolnym i zazwyczaj niema on sensownej interpretacji, więc nie interpretujemy go

Parametr α₁ informuje jak zmieni się wartość zmiennej
jeżeli zmienna
wzrośnie o jedną jednostkę. W naszym przypadku α₁ = 4 co oznacza, że jeżeli przeciętne miesięczne dochody wzrosną o tysiąc złotych to średnie tygodniowe wydatki na słodycze wzrosną o 4 zł.

Jest to zgodne z teorią ekonomii( znak estymatora), ponieważ wraz ze wzrostem dochodów, ludność dysponuje większymi zasobami finansowymi i jest skłonna tygodniowo przeznaczyć na zakupu dobra „luksusowego”- słodyczy więcej pieniędzy.

Wektor reszt liczymy jako różnicę

Posługuję się tabelką pomocniczą:

lata	Wartość empiryczna śr. tygodn. wydatków na sł. yt	Przeciętne miesięczne dochody	Wartość oszacowana wydatków	Reszta
1	18	1,0	20	-2
2	21	1,0	20	1
3	22	1,5	22	0
4	22	1,5	22	0
5	24	2,0	24	0
6	25	2,0	24	1
7	26	2,5	26	0
8	26	2,5	26	0
9	29	3,0	28	1
10	30	3,5	30	0
11	30	3,5	30	0
12	31	4,0	32	-1

Wektor reszt ma postać:

= [ -2 1 0 0 0 1 0 0 1 0 0 -1]

Suma reszt równa jest 0, więc spełnione jest założenie o wzajemnym znoszeniu się zakłóceń.

Tak więc wartość oczekiwana składnika losowego wynosi 0.

Teraz mogę przystąpić do policzenia błędu równania:

S.E.E. =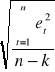
=
=

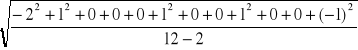
n=12 bo mamy 12 obserwacji

k=2 bo mamy dwa szacowane parametry

Średni błąd równania wynosi 0,89 co oznacza, że wartości oszacowane średnich tygodniowych wydatków na słodycze różnią się średnio od wartości empirycznych o 89 groszy.

Aby oszacować, czy różnica ta jest duża, czy mała obliczamy błąd procentowy:

MAPE=
=

Wartości oszacowanych średnich tygodniowych wydatków (w danych latach) na słodycze różnią się od wartości rzeczywistych średnio o 3,51%, co jest małym dopuszczalnym błędem.

Współczynnik determinacji obliczam ze wzoru:

Tak wiec w 100 % zmiany średnich tygodniowych wydatków na słodycze zależą od przeciętnych miesięcznych dochodów.

Druga metoda:

Mając wyliczone lub dane następujące wielkości

= [ -2 1 0 0 0 1 0 0 1 0 0 -1]

y_t=[18 21 22 22 24 25 26 26 29 30 30 31]

=
=

(przyjmę w tym wyliczeniu dla uproszczenia obliczeń
)

podstawiając do wzoru:

R²=1-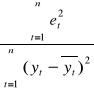
=

=1-

(Niewielka rozbieżność wynikach uzyskanych w obu metodach wynika zapewne z zaokrąglania liczb)

Tak wiec w niemal 100 % ( zależnie od przybliżenia 100, czy 96) zmiany średnich tygodniowych wydatków na słodycze (w danym roku) zależą od przeciętnych miesięcznych dochodów na osobę ( oszacowany model objaśnia tą zależność w bardzo dobry sposób)

Aby obliczyć średnie błędy wykorzystamy odchylenie standardowe reszt oraz macierz

=


=

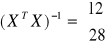
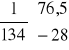
S.E.E. =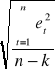
=
=

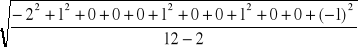
oraz oszacowane parametry strukturalne modelu, czyli:

a także wzór na średni błąd estymatora:

S(α_j)=S(a_j)=S_e

błąd liczę dla każdego parametru:

Odczytuję z macierz wartość:

Kolejno podstawiam do wzoru:

S(
)=S(a₀)=S_e

S(
)=S(a₁)=S_e

Zapisujemy, więc:

α₀= 16

α₁= 4
7,14^-3

Podsumowując:

Model spełnia wszystkie kryteria, jest modelem merytorycznym.

Model jest prawidłowy, R2 osiągnął bardzo wysoką wartość. Zmienna objaśniająca bardzo dokładnie określa zmiany zmiennej objaśnianej. Dobrze, więc została ona dobrana.

Wartość oczekiwana składnika losowego wynosi 0.

Średni błąd równania wynosi 0,89 co oznacza, że wartości oszacowane średnich tygodniowych wydatków na słodycze różnią się średnio od wartości empirycznych o 89 groszy.

Wartości oszacowanych średnich tygodniowych wydatków (w danych latach) na słodycze różnią się od wartości rzeczywistych średnio o 3,51%, co jest małym dopuszczalnym błędem.

Oceny parametrów są także precyzyjne.

Model wykazuje bardzo duże dopasowanie wartości teoretycznych do rzeczywistości.

Myślę, że model ten zaliczyć można do bardzo dokładnych, czyli udanych.

Zadanie 2

Do poprawnej interpretacji niezbędne jest porównanie jednostek występujących w modelu zmiennych. Zmienną objaśniającą jest realny PKB i stopa oprocentowania depozytów 12-miesięcznych, zmienną objaśnianą realna wartość konsumpcji ( będzie ona reagowała na zmiany PKB)

Parametr 60018,34 to wyraz wolny, mało istoty, niebrany pod uwagę przy interpretacji.

Parametr 0,14 odnoszący się do realnego PKB informuje, że jeżeli realny PKB wzrośnie o jedną jednostkę, czyli o 1 mln. zł, wówczas realna wartość konsumpcji wzrośnie o 140 000 tyś.zł.

Parametr -530,56 odnosi się do stopy oprocentowania depozytów 12-miesięcznych. Informuje on nas o tym, że jeśli stopy procentowe tych depozytów wzrosną o 1 punkt, wówczas realna wartość konsumpcji spadnie o 530,56 mln. zł.

Znaki te są zgodne z teorią ekonomii, ponieważ ze wzrostem PKB rośnie także wartość konsumpcji. Jeśli zaś stopy procentowe wzrastają potencjalni konsumenci są skłonni do lokowania swoich kapitałów w bankach ( np. w formie depozytów, lokat terminowych) w celu osiągnięcia jak największych zysków.

Wartość R² =0,903 oznacza, że powyższy model w 90,2% wyjaśnia zmienność realnej wartości konsumpcji. Jest to bardzo wysoki stopień co oznacza wysoki poziom dopasowania wartości teoretycznych do rzeczywistych.

S.E.E na poziomie 2347,67 oznacza, że wartości oszacowane realnych wartości konsumpcji różnią się średnio od wartości rzeczywistych o 2347,67 mln.zł.

Aby oszacować, czy różnica ta jest duża, czy mała obliczamy błąd procentowy:

MAPE=
=

Tak więc oszacowane wartości realnej konsumpcji różnią się średnio od wartości rzeczywistych o 3,92%. Możemy uznać, że jest to mały, dopuszczalny błąd.

:

Nie mogę ocenić dokładności estymatorów:

-dla wyrazu wolnego α₀=60018,34

-dla parametru przy realnym PKB α₁=0,14

-dla parametru przy stopie oprocentowania depozytów.. α₂=-530,56

gdyż nie mam wiadomości o średnich błędach estymatorów. Mogłabym je obliczyć posiadając informacje o macierzy
( pozostałe dane są znane).

W każdym razie, gdy α₀, α_1,α₂ przyjmują powyższe wartości model opisujący jak kształtuje się realna wartość konsumpcji jest poprawny. Dowodzą tego znaki, zgodne z prawidłowościami ekonomii. Model ten jest dokładny ( jest obarczony małym błędem) a także dobrze dopasowany.

.

Zadania

1

www.wkuwanko.pl

---