Temat Nr.10 - Teoria stateczności układów prętowych.

1. 
   Wiadomości wstępne.
   Zagadnienie stateczności jest jednym z ważnych problemów mechaniki budowli. W elementach ustrojów prętowych, tj. słupach ram i prętach kratownic, mogą wystąpić zmiany na skutek działania sił ściskających. Pod wpływem małej siły ściskającej pręt ulega skróceniu, a jego oś pozostaje prostoliniowa. Przy narastającej sile pojawia się stan równowagi chwiejnej, w którym przy drobnym zaburzeniu pręt nagle traci prostoliniowość i wyginając się ulega deformacji.
   
   
   Tę nagłą zmianę nazywamy wyboczeniem pręta. Zjawisko wyboczenia jest jedną z form utraty stateczności. Utrata stateczności może nastąpić wówczas, gdy siła osiowa P osiągnie pewną wartość krytyczną P_kr. Wartości tej towarzyszą zatem dwa stany równowagi odpowiadające prostoliniowej lub krzywoliniowej osi pręta.
   Obliczanie siły krytycznej w konstrukcjach prętowych umożliwia metoda przemieszczeń. W nauce o wytrzymałości materiałów wyprowadzono wzór Eulera, za pomocą którego oblicza się siły krytyczne pojedynczych, jednoprzęsłowych, prętów o stałym przekroju i stałej sztywności zginania (EI=const.), podpartych w jeden ze sposobów podanych na rys.1.
   
   
   
   
   
   
   
   
   
   
   W konstrukcjach ramowych siły krytyczne można obliczyć wzorem Eulera wówczas, gdy znamy długości wyboczeniowe l_w ściskanych prętów. Długości te można uzyskać, rozwiązując ramy metoda przemieszczeń. Tok obliczeń objaśni przykład ramy podanej na rys.2. Stosując w niej wymagany trzy więzy, równania kanoniczne przyjmą postać:
   
   
   
   
   
   
   
   
   
   
   
   W równaniach nie występują współczynniki od obciążeń zewnętrznych, jest to więc układ równań jednorodnych. Jednym rozwiązaniem jest takie rozwiązanie, że Z₁=Z₂=Z₃=0, odpowiada nie odkształconej postaci ramy, w której siła P_k=0, drugie natomiast otrzymujemy z warunku, że wyznacznik współczynników r_ik (macierz sztywności) jest równa zeru.
   Po obliczeniu wyznacznika i przyrównaniu go do zera otrzymamy równanie, z którego obliczymy poszukiwaną siłe krytyczną.
   

2. Zagadnienie Eulera.
   Podejmiemy próbę wyznaczenia siły krytycznej na podstawie analizy wygiętej postaci równowagi pręta. Jedyną przyczyną wygięcia osi pręta jest moment zginający
   
   obliczony po odstąpieniu od zasady zesztywnienia. Tak ustaloną funkcję momentu wprowadzimy do równania różniczkowego linii ugięcia. Założymy dodatkowo, że:
   − krzywizny wygiętej osi pręta są małe,
   − pomijamy wpływ sił poprzecznych,
   − pomijamy wpływ skrócenia osi pręta.
   Wszystkie wyżej wymienione założenia odpowiadają teorii wyboczenia pręta sprężystego, zbudowanej przez Eulera.
   
   
   
   Równanie różniczkowe linii ugięcia przyjmuje zatem następującą postać:
   
   
   
   
   skąd:
   
   
   
   
   gdzie
   . Ogólnym rozwiązaniem tego równania jest funkcja:
   
   
   
   
   
   
   
   
   
   
   Wobec tego
   
   
   
   
   Ponieważ na swobodnym końcu pręta
   , więc musi zachodzić warunek
   
   
   
   
   Z równania tego wynika, że albo Δ = 0, albo
   . Jeżeli Δ = 0, to w ≡ 0, a zatem nie ma wyboczenia. Jeżeli natomiast
   , to musi być spełniona zależność:
   
   
   
   
   Z tego równania wyznaczymy wartości
   , dla których może wystąpić wyboczenie. Ugięcie Δ pozostaje jednak nieokreślone. Uwzględniwszy, że
   ² = P / (EJ) , na podstawie równania (b) otrzymujemy:
   
   
   
   
   skąd
   
   
   
   
   Otrzymaliśmy zatem nieskończenie wiele rozwiązań. Z praktycznego punktu widzenia interesuje nas jednak tylko najmniejsza siła P(n), występująca dla n = 1. Jest to poszukiwana siła krytyczna:
   
   
   
   Wartości tej odpowiada tak zwana pierwsza postać wyboczenia (n=1), którą określa równanie:
   
   
   
   
   Trzy pierwsze postacie wyboczenia odpowiadające wartościom n=1, n=2 i n=3 na rysunkach:
   
   
   

3. Wzory transformacyjne do zagadnień stateczności
   
   Zestawienie wzorów transformacyjnych dla prętów obciążonych siłą osiową, EI - const
   
   1. Pręt obustronnie utwierdzony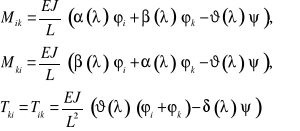
   
   
   
   
   2. Pręt jednostronnie utwierdzony drugostronnie przegubowy: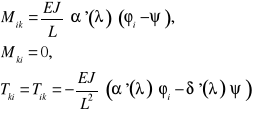
   
   
   
   
   
   3. Pręt utwierdzony jednostronnie oraz teleskopowo podparty drugostronnie: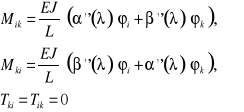
   
   
   
   
   
   
   
   4. Pręt jednostronnie utwierdzony - wspornik: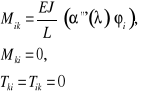
   
   
   
   
   
   W powyższych wzorach funkcje parametru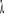
   określone są zależnościami: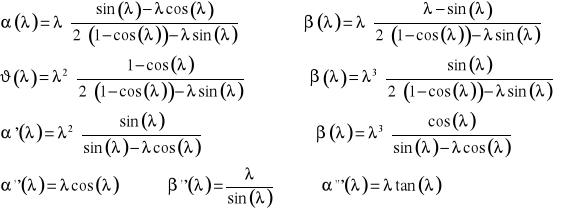
   
   Podane wzory stosuje się do ściskania. W przypadku rozciągania argument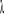
   staje się liczbą urojoną.
   
   

Rys.1.

Rys.2.

---