δ₁₁ δ_1n

D= macierz podatności

δ_n1 δ_nn

x₁

X= wektor niewiadomych

x₂

Δ_1p

D^F= wektor wyrazów wolnych

Δ_np

DX+D^F=0

M^h_ost = M^h₁x₁ + M^h₂x₂ + M^h₃x₃ + M^h_p

1.Wyznaczamy stopień statycznej niewyznaczalności

2.Tworzymy układ podstawowy metody sił (układ statycznie wyznaczalny- tworzymy przez usunięcie więzi nadliczbowych

3.Budujemy układ równań metody sił.Wyznaczamy współczynniki układu

4.Rozwiązujemy układ równań (wyznaczamy siły hiperstatyczne x_i)

5.Wyznaczamy rzędne ostatecznych wykresów M.,Q,N w punktach charakterystycznych

6.Sprawdzamy rozwiązanie

METODA PRZEMIESZCZEŃ

6. Metoda przemieszczeń

Procedura

*wyznaczenie stopnia kinematycznej (i geometrycznej) niezmienności układu

*UPMP

*układ równań MP (wyznaczamy współczynniki k)

*wyznaczamy M_ost

*sporządzamy wykres

8. Stateczność prętów prostych

Istota zjawiska utraty stateczności pręta prostego znana jest z kursu wytrzymałości materiałów.Występuje ono w przypadku działania na pręt siły osiowej S o tzw. wartości krytycznej S_kryt.Pręt znajduje się wówczas w stanie równowagi obojętnej; jego oś może pozostawać linią prostą,ale również nieskończenie mała dodatkowa przyczyna może wywołać jej wygięcie.Mówimy,że następuje wtedy wyboczenie pręta.Wartość krytyczną siły ściskającej dla swobodnie podpartego pręta o stałym przekroju poprzecznym wyznacza się na podstawie równania Euler'a:

w” + (SI²/EI)*w = 0

P_wyt = (Π²EI)/(μ*l²) - siła Eulerowska

Jeżeli smukłość rozważanego pręta jest większa od smukłości granicznej,to po osiągnięciu przez siłę S wartości krytycznej pręt ulega sprężystemu wyboczeniu.

Pręt ulegnie wyboczeniu przy dowolnejwartości obciążenia zewnętrznego.

W potocznym języku opór jaki stawia pręt zginany,przyjęto nazywać jego sztywnością.

Pręt rozciągany ma większą sztywność na zginanie niż pręt ściskany.

W przypadku gdy siła ściskająca ma wartość P_kr=Π²EI/(μ) sztywność pręta na zginanie jest równa 0.

Efekt polega na zmianie sztywności pręta na zginanie;ma to duże znaczenie w analizie statycznej złożonych ustrojów prętowych.

Stateczność płaskich ustrojów ramowych

K*Q=P

K-macierz sztywności

Q-wektor przmieszczeń

P-całkowity wektor obciążeń

Jeżeli założymy brak obciążeń wywołujących zginanie,wówczas wektor P=0, [K]=0

r₁₁б₁ + r₁₂Δ₂ = 0

r₂₁б₁ + r₂₂Δ₂ = 0

Postacie utraty stateczności

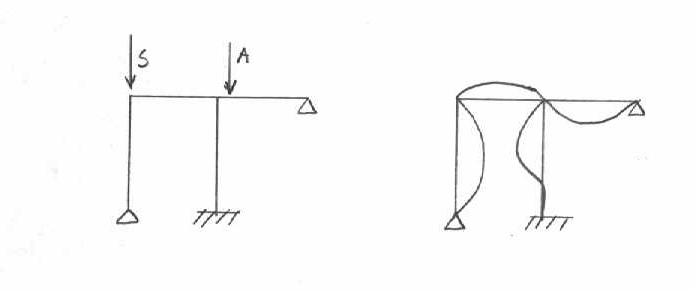
Konstrukcja znajduje się w stanie równowagi statycznej,jeśli po dowolnie małym odchyleniu od położenia pierwotnego konstrukcja wykazuje tendencje do powrotu do tego położenia pierwotnego.Utrata stateczności prowadzi do zniszczenia konstrukcji,gdyż pociąga za sobą duże odkształcenia i to w sposób nagły.

Aby konstrukcja znajdowała się w stanie równowagi statycznej muszą być spełnione warunki:

• konstrukcja musi być geometrycznie niezmienna

• obciążenie konstrukcji musi być mniejsze od P_kryt, przy którym następuje utrata stateczności

II.Postacie utraty stateczności:

Postać utraty stateczności zależy od przyłożonej siły oraz od geometrii ustroju

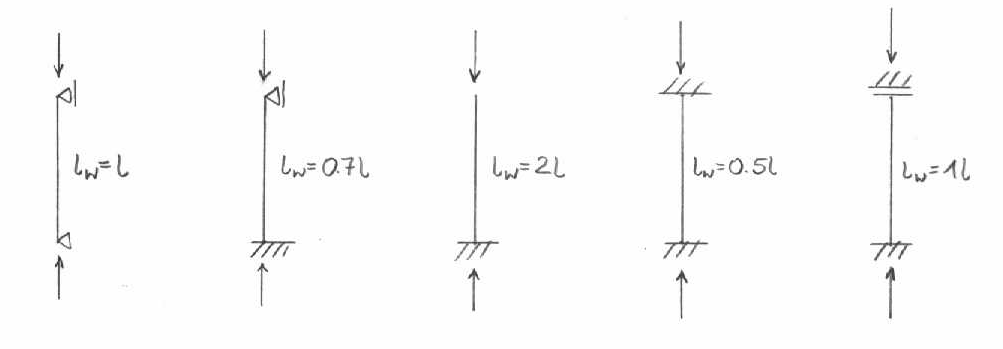
III.Metody określania sił krytycznych (zakres liniowo sprężysty)

* dla prętów prostych wzór Eulera P=Π²EI/l_w²

l_w - długość wyboczeniowa

• dla płaskich ustrojów ramowych: metoda przemieszczeń

Schemat postępowania:

1.Dobór układu podstawowego MP

2.Układ równań MP

3.Wyznaczenie współczynników- nowe wzory transformacyjne dla prętów obciążonych siłą osiową

Stateczność prętów prostych i płaskich ustrojów ramowych

Stateczność

Pojedynczych prętów Układy złożone

Pręt idealny z imperfekcją idealny z imperfekcją

7. Obciążenia różnych typów; wpływ temperatury, przemieszczenia wymuszonego, uwzględnienie sprężystego podparcia punktowego i ciągłego, wykorzystanie symetrii układu i obciążeń.

I.Typy obciążeń:

• statyczne - wartość zwiększa się od zera do wartości końcowej,usuwanie obciążenia na statyczne można związać z największym okresem drgań własnych konstrukcji.Jeżeli czas zmiany obciążenia jest znacznie większy od największego okresu drgań własnych konstrukcji,to można to nazwać statycznym

• dynamiczne - wartość zmienia się nagle lub okresowo zmiennie lub w chwili przyłożenia do konstrukcji jest skończona

Zależnie od czasu trwania i sposobu działania:

• stałe - wartość,kierunek i położenie pozostają niezmienne w czasie użytkowania budowli,jej montażu i remontu

• zmienne - mogą zmieniać wartość,kierunek lub położenie w czasie użytkowania budowli

-w całości długotrwałe- np.parcie wody o stałym poziomie zwierciadła

-w części długotrwałe- np.ciężar pyłu,obciążenie od suwnic

-w całości krótkotrwałe- np.śnieg,wiatr

• wyjątkowe - występują w wyniku mało prawdopodobnych zdarzeń w czasie użytkowania budowli (powódz,pożar)

II.Wpływ temperatury

Zmiana temperatury w stosunku do temperatury montażu powoduje wydłużenie pręta w osi lub :zginanie pręta momentami powstałymi na skutek gradientu temperatur.

Siły wewnętrzne powstające pod wpływem tego rodzaju obciążenia można obliczać za pomocą metody przemieszczeń, gdzie zadane przemieszczenie wynosi α*t*l,

α- współczynnik rozszerzalności termicznej

t - temperatura

l - długość pręta

lub metodą sił, w której wpływ temperatury uwzględniony jest przez Δ_it

δ₁₁x₁ + δ₁₂x₂ + Δ_1t = 0

δ₂₁x₁ + δ₂₂x₂ + Δ_2t = 0

Δ_it = Σ [ ∫N_i*α*t_c*ds. + ∫M*α*(ΔT/h)ds. ]

h - wysokość przekroju

∫N_i*α*t_c*ds. - równomierne ogrzanie

∫M*α*(ΔT/h)ds. - nierównomierne ogrzanie

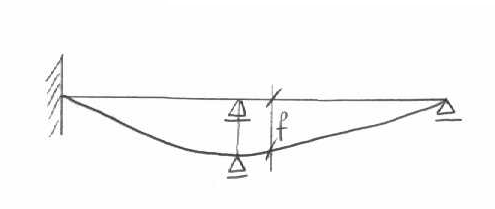
III.Wymuszone przemieszczenie

Siły wewnętrzne w układzie statycznie niewyznaczalnym,wynikłe z przemieszczenia podpór wylicza się za pomocą:

• metody przemieszczeń - przemieszczenie podpór f traktuje się jako obciążenie geometryczne stanowi osiadanie podpór lub wymuszone przemieszczenia węzłów

• metody sił - układ równań:

gdzie Δ_ip = 0 - brak obciążenia zewnętrznego

x₁δ₁₁ + x₂δ₁₂ + Δ_1p = -f

x₁δ₂₁ + x₂δ₂₂ + Δ_2p = 0

IV.Uwzględnienie sprężystego podparcia punktowego i ciągłego.

Podłoże sprężyste typu Winklera charakteryzuje parametr

k = c* b

c - moduł podatności podłoża

b - szerokość belki

np.

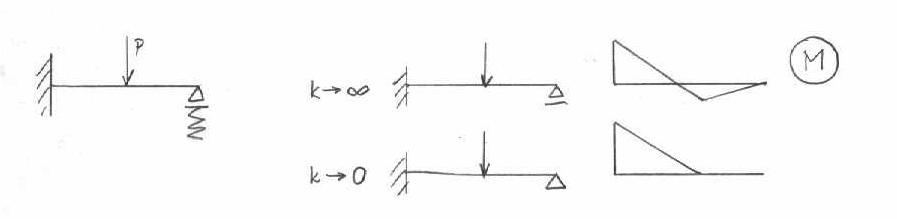
Podparcie ciągłe /podłoże Winklera/. Podstawowe założenia:

1.Podłoże składa się z nieskończenie wielu sprężyn,a odpór takiego podłoża jest wprost proporcjonalny do przemieszczenia

2.Brak siły tarcia między belką a podłożem /więzy gładkości/

3.Więzy przenoszą zarówno ściskanie jak i rozciąganie

Zgodnie z zał. zagadnienie sprowadza się do obliczenia belki obciążonej jak na rys.

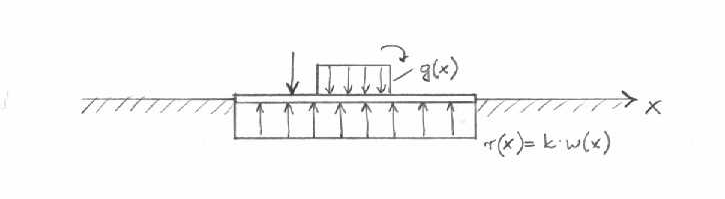
Pod wpływem przyłożonego obciążenia punkty belki doznają przemieszczeń,które związane są z momentami zginającymi EI*w''(x) = -M.(x)

Wiedząc,że M.''(x) = -q(x) + k*w(x) równanie różniczkujemy, przekształcamy itd. i w rezultacie otrzymujemy równania na w(x).

Mając dane obciążenie oraz warunki brzegowe, znamy przemieszczenia,znajdujemy funkcję momentów i sił poprzecznych.Tak rozwiązuje się belki o nieskończonej długości.

V.Wykorzystanie symetrii układu

W przypadku układów symetrycznych stosuje się schematy połówkowe,które mają mniej stopni statycznej niewyznaczalności niż układ pierwotny.Schematy połówkowe obciąża się obciążeniem rozbitym na: obciążenie symetryczne i antysymetryczne .Ostateczny wykres sił wewnętrznych otrzymuje się przez zsumowanie wykresów z symetrii i antysymetrii.

---