Tatiana Zaszkowska 22 XI 2001

Ćwiczenie nr 11

Temat: Wyznaczanie częstości własnych wahadeł sprzężonych. Wyznaczanie częstości rezonansowej wahadeł sprzężonych.

d=0,1m

m=0,1kg

Teoria:

Oscylatorami (wahadłami) sprzężonymi nazywamy dwa ciała zawieszone na sztywnych prętach sprzężonych za pośrednictwem sprężyny. Niech dwa identyczne wahadła mają masę m zawieszoną w odległości l od punktu zawieszenia, a sprężyna o współczynniku k jest zamocowana w odległości d od punktu zawieszenia. Jeżeli jedno z wahadeł wychylimy z położenia równowagi o kąt
, to wahadło drugie wychyli się o kąt
, a sprężyna wydłuży się o
. Jeżeli kąty są małe, to można przyjąć, że:

,

,

Można zatem zapisać następujące równania ruchu dla wahadeł:

Dodając i odejmując stronami otrzymujemy:

Wprowadzając nowe zmienne otrzymujemy układ równań niezależnych:

,

gdzie
,
.

Rozwiązaniem są równania:

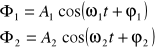
Każdy ruch wahadeł sprzężonych przy małych wychyleniach z położenia równowagi jest superpozycją dwóch drgań o różnych częstościach własnych. Można rozważać dwa przypadki wychyleń wahadeł.

1. Drgania synfazowe wahadeł sprzężonych - wahadła wykonują drgania w tej samej fazie i o tej samej częstości własnej, wychylone zostały w tym samym kierunku o jednakowy kąt.

2. Drgania przeciwfazowe wahadeł sprzężonych - wahadła wychylamy o ten sam kąt, lecz w przeciwne strony, drgać będą one w tej samej fazie i z częstością

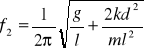
Korzystając z tych zależności można wyprowadzić wzór roboczy postaci:

11 a Zasada pomiaru

Przyrząd składa się z dwóch wahadeł z zawieszoną masą m sprzężonych ze sobą za pomocą sprężyny. Ma wbudowany układ mierzący czas i ilość okresów drgań. Wahadła wychylamy najpierw o kąt 6^o w tym samym kierunku, a następnie w przeciwnym. Obliczamy stałą sprężystości ze wzoru roboczego.

Obliczenia

, dla l=0,43 m

, dla l=0,38 m

, dla l=0,33 m

wartość średnia

SZACOWANIE NIEPEWNOŚCI POMIARU

Niepewność całkowita dla m:

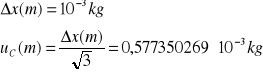
Niepewność całkowita dla l i d:

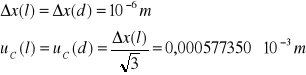
Dla k₁

Niepewność całkowita dla t₁:

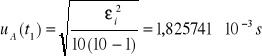
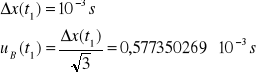
Niepewność całkowita dla t₂:

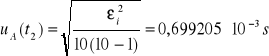
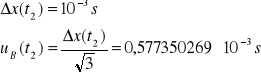
Dla k₂

Niepewność całkowita dla t₁:

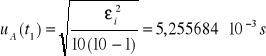
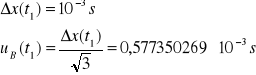
Niepewność całkowita dla t₂:

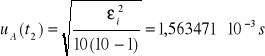
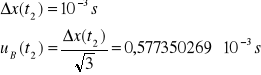
Dla k₃

Niepewność całkowita dla t₁:

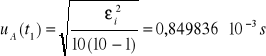
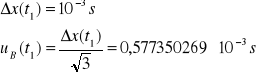
Niepewność całkowita dla t₂:

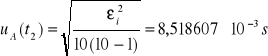
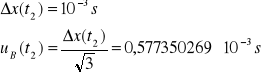
Wartości pochodnych cząstkowych

Dla k₁

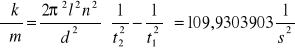
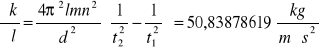
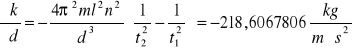
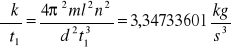
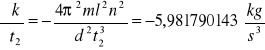
Dla k₂

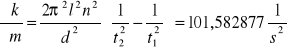
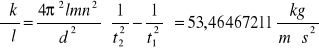
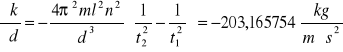
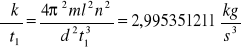
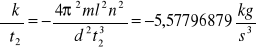
Dla k₃

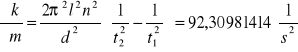
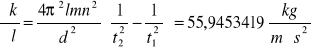
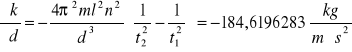
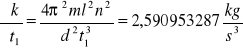
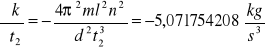
Niepewności całkowite dla k

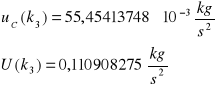
Uśredniając wyniki otrzymujemy

Ostateczny wynik

11 b Zasada pomiaru

Te same wahadła łączymy teraz sprężyną do pręta, który jest sprzężony z silnikiem. Silnik , będący siłą wymuszającą, wprawia pręt w ruch, a ten przekazuje energię wahadłom, które zaczynają drgać. Przy amplitudzie około 20⁰ zachodzi zjawisko rezonansu. Częstość rezonansową można wyznaczyć ze wzoru:
.

Obliczenia

Uśredniając wszystkie trzy wartości otrzymujemy:

SZACOWANIE NIEPEWNOŚCI POMIARU

Dla f₁

Niepewność całkowita dla t:

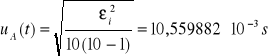
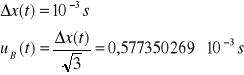
Pochodne cząstkowe:

Niepewność rozszerzona

Dla f₂

Niepewność całkowita dla t:

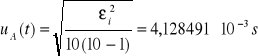
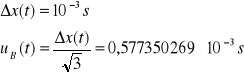
Pochodne cząstkowe:

Niepewność rozszerzona

Dla f₃

Niepewność całkowita dla t:

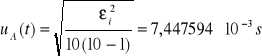
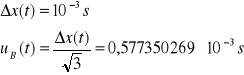
Pochodne cząstkowe:

Niepewność rozszerzona

Uśredniając niepewność rozszerzoną otrzymujemy:

Ostateczny wynik

Wnioski

Doświadczalne wyznaczenie częstości rezonansowej wahadeł sprzężonych było niełatwe. Wynikało to przede wszystkim z trudności uzyskania rezonansu przy danej amplitudzie 20⁰. Przy takim wychyleniu wahadła za szybko drgały i psuło się połączenie sprężyste. Dlatego doświadczenie przeprowadzaliśmy przy mniejszej amplitudzie około 16⁰.

4

---