 | Pobierz cały dokument zastosowania.pochodnej.matematyka.i.doc Rozmiar 408 KB |
ZASTOSOWANIA RACHUNKU RÓŻNICZKOWEGO
Pojęcie pochodnej funkcji jest podstawowym pojęciem analizy matematycznej i ma szerokie zastosowania. Definicję pochodnej podali niezależnie od siebie Newton, w związku z rozważaniami dotyczącymi prędkości ruchu punktu materialnego, oraz Leibniz, przy rozpatrywaniu zagadnienia stycznej do krzywej.
Kinematyczną (fizyczną) interpretacją pochodnej jest prędkość chwilowa w ruchu prostoliniowym.
Przypuśćmy, że ciało porusza się po linii prostej, przebywając pewną drogę od punktu początkowego O. Prędkość średnia tego ciała w odstępie czasu ![]()
wyliczmy z dobrze znanego nam wzoru
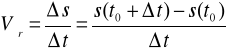
Ale jeśli byśmy chcieli znać dokładną wartość prędkości ciała w momencie t0 musielibyśmy liczyć ją, gdy przyrost czasu![]()
jest znikomy, tzn. gdy ![]()
, czyli
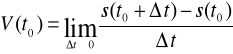
Oznacza to, że prędkość ciała w dowolnym momencie jest pochodną funkcji s(t), której wartość określa drogę przebytą w czasie t (zob. definicja pochodnej funkcji).
Definicja.
Niech dana będzie funkcja f : A→R, A⊂R. Jeżeli istnieje granica skończona
![]()
to granicę tę nazywamy pochodną funkcji f w punkcie x0 i oznaczamy najczęściej symbolem f '(x0).
Iloraz
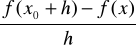
przyrostu wartości funkcji do przyrostu argumentu nazywamy ilorazem różnicowym funkcji.
Wzory na pochodne wybranych funkcji znajdują się w dołączonej tablicy.
I. Różne interptetacje pochodnej
1. Interpretacja geometryczna. Równanie stycznej
Jeżeli funkcja f jest ciągła w punkcie x0 i ma w tym punkcie pochodną f '(x0), to do wykresu tej funkcji istnieje w punkcie (x0, f(x0)) styczna o równaniu
y-f(x0)=f '(x0)(x- x0).
Styczna ta jest granicą siecznych przechodzących przez punkty A(x0, f(x0)) oraz
B(x0+h, f(x0+h)) przy h zmierzającym do 0. Fakt ten ilustruje poniższy rysunek.
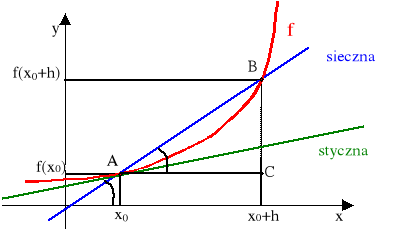
Długość odcinka BC jest równa przyrostowi wartości funkcji f odpowiadającego przyrostowi argumentu o h (długość odcinka AC). Iloraz różnicowy funkcji jest więc stosunkiem długości odcinków BC do AC. Jest on zatem równy tangensowi kąta α nachylenia siecznej AB do osi OX, co oznacza, że w sensie geometrycznym jest on równy współczynnikowi kierunkowemu siecznej AB.
 | Pobierz cały dokument zastosowania.pochodnej.matematyka.i.doc rozmiar 408 KB |