POLITECHNIKA ŚLĄSKA W GLIWICACH

Wydział Elektryczny

Kierunek Elektronika i Telekomunikacja

Inżynierskie, niestacjonarne, zaoczne, sem. 2

LABORATORIUM Z FIZYKI

Temat ćwiczenia :

Wyznaczanie lepkości powietrza

Sekcja 02

Łukasz Antecki

Piotr Antończyk

Jacek Gajoch

Gliwice 2011

1. WSTĘP lub WPROWADZENIE

1.1 Lepkość (tarcie wewnętrzne) - właściwość płynów i plastycznych ciał stałych charakteryzująca ich opór wewnętrzny przeciw płynięciu. Lepkością nie jest opór przeciw płynięciu powstający na granicy płynu i ścianek naczynia. Lepkość jest jedną z najważniejszych cech płynów (cieczy i gazów).

1.2 Ciśnienie - wielkość skalarna określona jako wartość siły działającej prostopadle do powierzchni podzielona przez powierzchnię na jaką ona działa, co przedstawia zależność:

1.3 Prawo Hagena-Poiseuille'a - prawo fizyczne opisujące zależność między strumieniem objętości cieczy a jej lepkością (która wynika z tarcia wewnętrznego), gradientem ciśnień (który jest bodźcem termodynamicznym powodującym przepływ płynu), a także wielkościami opisującymi wielkość naczynia (długość, promień przekroju poprzecznego).

Przy stacjonarnym (tj. niezmiennym w czasie), laminarnym przepływie nieściśliwego, lepkiego płynu w cylin­drycznym przewodzie (tj. w rurze o stałym, kołowym przekroju), strumień objętości przepływu (objętość przepły­wającego płynu na jednostkę czasu) propor­cjonalny jest do gradientu ciśnienia wzdłuż przewodu, a zatem i do różnicy ciśnień na końcach przewodu:

gdzie poszczególne symbole oznaczają:

ΦV - strumień objętości przepływu,

V, dV/dt - objętość, pochodna objętości względem czasu,

z - współrzędna walcowa, długość liczona wzdłuż osi przewodu,

vs - średnia prędkość płynu w kierunku z,

r - promień wewnętrzny przewodu,

η - współczynnik lepkości dynamicznej płynu,

p - ciśnienie uśrednione w przekroju przewodu,

-dp/dz - gradient ciśnienia wzdłuż osi z,

Δp - różnica ciśnień na końcach przewodu,

l - długość przewodu.

1.4 Rodzaje przepływów:

-Przepływ laminarny jest to przepływ uwarstwiony (cieczy lub gazu), w którym kolejne warstwy płynu nie ulegają mieszaniu (w odróżnieniu od ruchu turbulentnego, burzliwego). Przepływ taki zachodzi przy małych prędkościach przepływu, gdy liczba Reynoldsa nie przekracza tzw. wartości krytycznej.

-Przepływ stacjonarny (ang. steady flow) - ruch płynu, w którym składowe wektora prędkości nie są funkcjami czasu. Inaczej mówiąc, przepływ stacjonarny to ruch płynu nie zmieniający się w czasie. Przeciwieństwem przepływu stacjonarnego jest przepływ niestacjonarny.

W przepływie stacjonarnym cząstki płynu poruszają się po liniach prądu, tj. linie prądu pokrywają się z trajektoriami cząstek płynu.

Przepływ stacjonarny może odbywać się z różnymi, na ogół niezbyt wysokimi prędkościami. Jednym z warunków jego istnienia jest zachowanie laminarności przepływu.

-Turbulencja, przepływ burzliwy - w mechanice ośrodków ciągłych, reologii i aerodynamice - określenie bardzo skomplikowanego, nielaminarnego ruchu płynów. Ogólniej termin ten oznacza złożone zachowanie dowolnego układu fizycznego, czasem zachowanie chaotyczne. Ruch turbulentny płynu przejawia się w występowaniu wirów i innych struktur koherentnych, zjawisku oderwania strugi, zjawisku mieszania.

1.5 Manometr cieczowy

Za pomocą manometrów U - rurkowych można mierzyć nadciśnienie, podciśnienie oraz różnicę ciśnień w zależności od sposobu przyłączenia. Jest to najprostszy manometr służący do pomiaru technicznych ciśnień, w tym m.in. do pomiaru małej różnicy ciśnień, jak np. przy przepływie płynów przez zwężkę. Najważniejszą częścią tego manometru (rys. 4) jest rurka szklana (1) zgięta na kształt litery U, deska mocująca (2) oraz podziałka milimetrowa (3).

Zasada działania manometrów U - rurkowych oparta jest na równości ciśnień na poziomych powierzchniach ekwipotencjalnych w naczyniach połączonych. Pomiarowi podlega przesunięcie słupa cieczy manometrycznej (spiętrzenie) h. Wobec tego, że na poziomie niższej powierzchni cieczy ciśnienia w obu ramionach są jednakowe, toP1=

P1=γ*h+P2 , a różnica ciśnień wynosi: P2-P1=ΔP=γ*h=σ*g*h W trakcie pomiarów tym przyrządem należy unikać wychyleń (wysokości słupa) mniejszych od 100 mm, ze względu na zmniejszającą się dokładność pomiarów. Dla określonego ciśnienia wychylenie to zależy od gęstości użytej cieczy. Do mierzenia niedużych ciśnień należy stosować ciecze o małej gęstości.

γ - ciężar właściwy cieczy manometrycznej [N/m³]

2. STANOWISKO POMIAROWE

Gdzie: Zawór Szklana butla z wodą Rurka kapilarna Filtr osuszający Manometr wodny Dane pomiarowe: Promień rurki kapilarnej r= 0,4 mm Długość rurki kapilarnej l= 117 mm Temperatura otoczenia T=20 stopni Celsjusza Ciśnienie atmosferyczne p= 1008 hPa Skala menzurki= 5 ml Menisk 1mm

Przebieg ćwiczenia

1 - odkręcenie zaworu spustowego tak, aby różnica poziomów na manometrze cieczowym wynosiła około 20mm

2 - spuszczenie z butli 400 ml wody oraz pomiar czasu

3 - pięciokrotne powtórzenie pomiaru czasu

4 - odczytanie temperatury w pomieszczeniu oraz ciśnienia powietrza

5 - obliczenie różnicy ciśnień na końcach manometru

6 - wyznaczenie współczynnika lepkości powietrza

7 - obliczenie średniej ważonej współczynnika lepkości powietrza

8 - obliczenie gęstości powietrza

9 - obliczenie prędkości przepływu powietrza przez kapilarę

10 - obliczenie liczby Reynoldsa

11 - oszacowanie niepewności pomiarowych

12 - Porównanie wyników obliczonych z wynikami tablicowymi

13 - opracowanie wyników końcowych oraz wniosków

3. WYNIKI POMIARÓW (BADAŃ)

Wykonane zostało 5 serii pomiarowych. W każdej serii staraliśmy się uzyskać takie same warunki pomiarów - różnica ciśnienia, prędkość przepływu. W każdej serii pomiarowej z butli zostało upuszczone 400 ml wody. Za każdym razem odczytywaliśmy różnicę poziomów w manometrze cieczowym na początku pomiaru i na końcu, ponieważ, ze względu na nieszczelność butli poziomy te były różne.

Pomiary te były wykonywane w warunkach:

-ciśnienie atmosferyczna - 1008 hPa

-temperatura otoczenia - 20 stopni C

LP	Czas w sekundach	Ilość wody ml	Różnica poziomów mm	Różnica poziomów
1	385,16	410	21-17 mm	4 mm
2	333,13	407	25-22 mm	3 mm
3	359,88	405	23-19 mm	4 mm
4	315,72	400	25-23 mm	2 mm
5	342,72	405	24-22 mm	2 mm

4. Obliczenia

4.1.1 Obliczanie różnicy ciśnień na końcach manometru:

p  ρgh - wzór ogólny

p - gęstość wody - 998 kg/m³

Dh - różnica poziomów wody w manometrze

p=998kg/m³ * 9,8 m/s² * 0,019m

p= 185,8276 kg/m*s² =Pa

Jako, że dla reszty obliczenia wyglądały analogicznie poniżej przedstawimy jedynie same wyniki:

p₁=185,8276 Pa

p₂=229,8394 Pa

p₃=205,3884 Pa

p₄=234,7296 Pa

p₅=224,9492 Pa

4.1.2 Opracowanie niepewności

Pa

Pa

Pa

Pa

Pa

4.1.3 Współczynnik lepkości powietrza. Prawo Poiseuille'a.

Gdzie:

r- średnica kapilary

ρ_w-gęstość wody

g -przyśpieszenie ziemskie

l - długość kapilary

V - prędkość przepływu cieczy

h - różnica poziomów w manometrze

t - czas wylewania cieczy

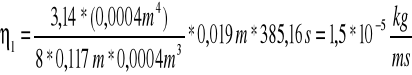
Jako, że dla reszty obliczenia wyglądały analogicznie poniżej przedstawimy jedynie same wyniki:

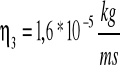
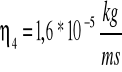
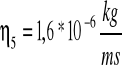
4.1.4 Opracowanie niepewności:

U(t)=0,15s

U(V)=0,005l

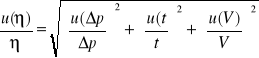
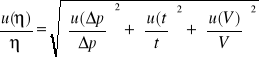
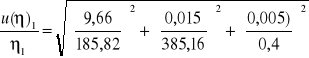
=0,0647
=0,0647*
=9,7*10^-7

0,0608

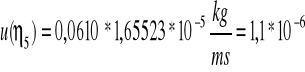
4.1.5 Obliczanie średniej ważonej współczynnika lepkości.

Gdzie:

w-waga pomiaru

PN-wartość zmierzona

Korzystając z przedstawionego powyżej wzoru obliczamy średnią ważoną lepkościi. Ze względu na bardzo rozbudowany sposób obliczeń przedstawiamy jedynie wynik końcowy. Średnią możemy obliczyć mając obliczone wagi dla każdego pomiaru oraz mając dane wartości lepkości każdego pomiaru. W naszym przypadku średnia ważona lepkości jest równa:

1,63416 * 10^-5 kg/ms = 1,6* 10^-5 kg/ms

Niepewność średniej ważonej współczynnika lepkości.

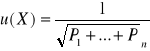
Niepewność wynosi: 0,00067= 6,7*10^-4

4.1.6 Obliczanie gęstości powietrza:

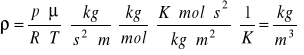
gdzie:

R - stała gazowa

T - temperatura

 - masa molowa gazu

p - ciśnienie powietrza

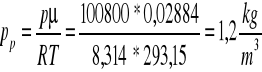
4.1.7.Obliczanie niepewności gęstości powietrza:

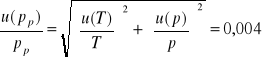
=0,00439*1,19=0,005

4.1.8 Obliczanie prędkości przepływu powietrza przez kapilarę:

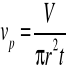
Gdzie:

V- objętość płynu który wypłynął [m³]

t- czas w którym płyn wypłynął [s]

r- promień kapilary [m]

Jako, że dla reszty obliczenia wyglądały analogicznie poniżej przedstawimy jedynie same wyniki:

Vp1=2,0 m/s

Vp2= 2,4m/s

Vp3= 2,2m/s

Vp4= 2,5 m/s

Vp5= 2,3 m/s

5 Opracowanie niepewności pomiaru

=0,051*2,0=0,1 m/s

=0,0503*2,3 =0,1 m/s

=0,046*2,3=0,1 m/s

=0,054*2,3=0,1 m/s

=0,047*2,3=0,1 m/s

5.1.1 Obliczanie liczby Reynoldsa:

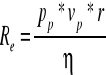
gdzie:

Pp = (1,19± 0,05) [kg/m³] - gęstość powietrza

Vp = (2,0 ± 0,27) [m/s].- prędkość przepływu powietrza

r = (0,0004 ± 0000,001) [m] - promień kapilary

η = (1,6 ± 1) ×10^{- 6} [kg/(s×m)] - lepkość powietrza

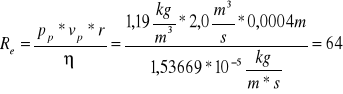
1. Re=64,1

2. Re=69.3

3. Re=66,9

4. Re=75,2

5. Re=66,9

Niepewność liczby Reynoldsa.

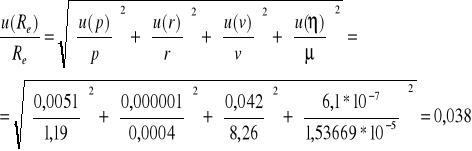
p= gęstość powietrza

v= prędkość przepływu powietrza

r= promień kapilary

η= lepkość

1)
=0,0038*64=2,4

2)
=2,5

3)
=2,4

4)
=2,7

5)
=2,3

6. Porównanie wyników obliczonych oraz tablicowych

Lepkość powietrza tablicowa -

Lepkość powietrza obliczona -

Liczba Reynoldsa tablicowa :

Przepływ laminarny- Re < 2300

Przepływ przejściowy - 2300 < Re < 10 000

Przepływ turbulentny - 10 000 < Re

Liczba Reynoldsa obliczona - 64

7. PODSUMOWANIE I WNIOSKI

Przepływ cieczy przez zawór powinien być stały. Niestety tak nie było gdyż zmieniała się prędkość wypływu wody z butli (zmniejszała się wraz ze spadkiem wody). Większą dokładność ćwiczenia można by uzyskać zwiększając znacznie przekrój butli z wodą tak, aby w czasie wypływu wody z butli poziom zmniejszał się minimalnie. Ponadto przedstawione wyniki pomiarowe oraz rezultaty obliczeń sugerują, iż miał miejsce duży błąd pomiarowy. Lepkość powietrza wynikająca z naszych obliczeń jest bardzo bliska idealnym wartościom tablicowym przedstawionych w tablicach fizycznych. Jako grupa stwierdzamy iż przyczyną nieznacznej różnicy może być rozszczelnienie naczynia w którym była woda, co powoduje powstanie „współczynnika” w przybliżeniu równego 20. Twierdzimy, że kolejną przyczyną błędów w naszych wynikach, które jednak nie powodują już tak znacznego wpływu na wyniki był menisk (1mm) oraz reakcja człowieka, która odgrywała rolę podczas włączania i wyłączania stopera (0.15 sek.) Z przeprowadzonych pomiarów wynika, że różnica poziomu ciśnienia jest proporcjonalna do czasu przepływu cieczy tzn. że im dłużej ciecz przepływała, tym większa była różnica ciśnień między nimi. Jedynie w przypadku ostatniego pomiaru wspomniana zależność nie miała miejsca. Z obliczeń dotyczących liczby Reynoldsa wynika, iż nasz przepływ wody klasyfikuje się w grupie przepływu laminarnego (Re < 2300). Jest to zgodne z prawdą gdyż podczas przepływu wody w naszym przypadku nie miały miejsca żadne ruchy wirowe. Po analizie przedstawionych wyników oraz pomiarów nasza grupa stwierdza, iż badanie przebiegło pomyślnie.

---