POLITECHNIKA ŚLĄSKA W GLIWICACH

Wydział Elektryczny

Kierunek Elektronika i Telekomunikacja

Inżynierskie, niestacjonarne, zaoczne, sem. 2

LABORATORIUM Z FIZYKI

Temat ćwiczenia: Sprawdzenie prawa Hooke'a. Metoda statyczna i dynamiczna.

Grupa 02

Antecki Łukasz
Antończyk Piotr
Gajoch Jacek

Gliwice 2011

1. Wstęp

Celem ćwiczenie laboratoryjnego jest wyznaczenie współczynnika sprężystości dwóch sprężyn, na których zawieszono różne obciążenia, w postaci niewielkich ciężarków. Ponieważ nie można określić tej wielkości wprost, należy posłużyć się prawem Hooke'a.

Prawo Hooke'a mówi jak bardzo odkształca się ciało w miarę naprężania. Zależność jest taka, że stopień odkształcenia jest wprost proporcjonalny do przyłożonej siły naprężającej. Jeśli zawiesimy pewną masę na sprężynie, to dojdzie do odkształcenia tej sprężyny w postaci rozciągnięcia jej na pewną długość. Zależność opisuje poniższy wzór:

Gdzie: F - przyłożona siła, k - współczynnik sprężystości sprężyny, x - wydłużenie sprężyny

Wielkością przez nas poszukiwaną jest oczywiście współczynnik sprężystości k, który wyznaczymy na podstawie dwóch metod sprawdzających prawo Hooke'a: statycznej i dynamicznej.

Metoda statyczna polega na zawieszaniu na sprężynach niewielkich odważników o masie 25g i 50g, aż do uzyskania masy 150g na jednej sprężynie i 300g na drugiej. Po zawieszeniu odważnika należy zmierzyć długość na jaką rozciągnęła się sprężyna. Pomiar długości rozciągnięcia sprężyny dla każdej masy należy przeprowadzić 10 razy.

Metoda dynamiczna polega na zawieszeniu na sprężynie odważnika o masie 50g, naciągnięciu sprężyny na długość nie przekraczającej 2cm i swobodnym puszczeniu. Następnie należy rejestrować czas pięćdziesięciu okresów ruchu sprężyny.

Dzięki metodzie statycznej i dynamicznej całość ćwiczenia sprowadza się jedynie do zmierzenia długości rozciągnięcia sprężyny oraz do zmierzenia czasu 50 okresów ruchu sprężyny. Żądaną wartość współczynnika sprężystości k wyliczymy stosując wzory fizyczne i zależności przedstawione w późniejszych rozdziałach.

W trakcie przeprowadzania ćwiczenia zostaną wykorzystane dwie sprężyny, z tym że obydwie do metody statycznej, a tylko jedna do metody dynamicznej.

2. Stanowisko pomiarowe

Do wykonania ćwiczenia niezbędne są: przyrząd do badania prawa Hooke'a z podziałką milimetrową, dwie sprężyny o różnych gęstościach zwoi (współczynnikach sprężystości), stoper elektroniczny, „wiaderko” z haczykiem, 6 sztuk niewielkich odważników o masie 50g, oraz kilka odważników o masie 25g.

Rysunek 1 Przyrząd do badania prawa Hooke'a

Metoda statyczna:

Ćwiczenie rozpoczynamy od zawieszenia sprężyn na przyrządzie. Do sprężyn należy dowiesić „wiaderko”, a na nie z kolei zakładamy odważnik o masie 50g. Następnie możemy przystąpić do pomiaru wydłużenia sprężyny. Aby nie popełnić błędu paralaksy, wykorzystamy tutaj „wiaderko”. Odczytując pomiar, należy patrzeć tak, aby linia podziałki na przyrządzie pokrywała się z dwoma brzegami „wiaderka”. Następnie można dowiesić kolejny ciężarek o tej samej masie i postępować analogicznie aż do masy 300g. Pomiar dla każdej masy musi być przeprowadzony 10 razy. Następnie powtarzamy to samo dla drugiej sprężyny, z tym że zmieniamy obciążenie co 25g, do uzyskania masy 150g.
Należy tutaj zaznaczyć, że nie udało nam się doprowadzić do sytuacji, kiedy brzegi „wiaderka” pokrywałyby się z linią 0 na podziałce, dlatego w naszych pomiarach zawsze musieliśmy odjąć nadwyżkę odległości. Wynikało z to z faktu, że przyrząd był za niski.

Metoda dynamiczna:

Ćwiczenie zaczynamy od zawieszenia ciężarka o masie 50g na sprężynie. Następnie naciągamy sprężynę na odległość nie większą niż 2 cm i puszczamy swobodnie. W momencie puszczenia sprężyny należy włączyć stoper. Dalej należy zliczać kolejne okresy ruchu sprężyny, a gdy liczba ta wyniesie 50, można zatrzymać stoper. Próbę należy powtórzyć 5 razy.

3. Wyniki pomiarów

W tym rozdziale zaprezentujemy uzyskane przez nas wyniki pomiarów dla metody statycznej oraz dynamicznej.

Metoda statyczna:

Sprężyna nr 1

Masa [kg]	0,050	0,100	0,150	0,200	0,250	0,300
Wychylenie [m]	0,029	0,059	0,091	0,121	0,154	0,185
		0,031	0,064	0,098	0,130	0,165	0,195
		0,031	0,064	0,101	0,130	0,163	0,196
		0,030	0,064	0,096	0,130	0,161	0,196
		0,032	0,064	0,098	0,131	0,165	0,198
		0,030	0,064	0,097	0,130	0,164	0,195
		0,031	0,063	0,099	0,129	0,162	0,200
		0,030	0,063	0,097	0,129	0,162	0,196
		0,031	0,063	0,099	0,130	0,158	0,197
		0,030	0,063	0,097	0,130	0,163	0,196

Sprężyna nr 2

Masa [kg]	0,025	0,050	0,075	0,100	0,125	0,150
Wychylenie [m]	0,039	0,076	0,116	0,154	0,191	0,230
		0,083	0,122	0,162	0,201	0,240	0,281
		0,084	0,126	0,161	0,202	0,242	0,280
		0,081	0,127	0,162	0,201	0,241	0,279
		0,083	0,124	0,165	0,202	0,242	0,278
		0,085	0,125	0,163	0,200	0,239	0,279
		0,083	0,124	0,162	0,200	0,240	0,277
		0,084	0,127	0,166	0,199	0,239	0,280
		0,084	0,129	0,166	0,200	0,241	0,281
		0,083	0,124	0,166	0,201	0,240	0,280

Metoda dynamiczna, masa obciążenia 50g

	Czas [s]
1.	22,29
2.	22,16
3.	22,2
4.	22,19
5.	22,25

4. Opracowanie wyników pomiaru

Jak podaliśmy wyżej, celem ćwiczenia jest określenie współczynnika sprężystości sprężyn. Jeśli chodzi o metodę statyczną, to współczynnik sprężystości możemy wyznaczyć za pomocą regresji liniowej. W metodzie dynamicznej należy uśrednić czas pięćdziesięciu okresów, dalej z niego wyliczyć okres T.

4.1 Metoda statyczna

W poniższych tabelach umieściliśmy zależność ciężaru wyrażonego w niutonach od masy wyrażonej w kilogramach. Należy zauważyć, że ciężar potraktowaliśmy jako iloczyn masy i przyśpieszenia ziemskiego, którego wartość przyjęliśmy jako
.

Metoda statyczna, sprężyna nr 1:

Masa [kg]	0,050	0,100	0,150	0,200	0,250	0,300
Ciężar [N]	0,490	0,980	1,470	1,960	2,450	2,940
Wychylenie [m]	0,029	0,059	0,091	0,121	0,154	0,185
		0,031	0,064	0,098	0,130	0,165	0,195
		0,031	0,064	0,101	0,130	0,163	0,196
		0,030	0,064	0,096	0,130	0,161	0,196
		0,032	0,064	0,098	0,131	0,165	0,198
		0,030	0,064	0,097	0,130	0,164	0,195
		0,031	0,063	0,099	0,129	0,162	0,200
		0,030	0,063	0,097	0,129	0,162	0,196
		0,031	0,063	0,099	0,130	0,158	0,197
		0,030	0,063	0,097	0,130	0,163	0,196
Średnie wychylenie x [m]	0,031	0,063	0,097	0,129	0,162	0,195

Zgodnie z wytycznymi zostaje wykreślona funkcja wychylenia od ciężaru:

Analogicznie dla drugiej sprężyny

Metoda statyczna, sprężyna nr 2

Masa [kg]	0,025	0,050	0,075	0,100	0,125	0,150
Ciężar [N]	0,245	0,490	0,735	0,980	1,225	1,470
Wychylenie [m]	0,039	0,076	0,116	0,154	0,191	0,230
		0,083	0,122	0,162	0,201	0,240	0,281
		0,084	0,126	0,161	0,202	0,242	0,280
		0,081	0,127	0,162	0,201	0,241	0,279
		0,083	0,124	0,165	0,202	0,242	0,278
		0,085	0,125	0,163	0,200	0,239	0,279
		0,083	0,124	0,162	0,200	0,240	0,277
		0,084	0,127	0,166	0,199	0,239	0,280
		0,084	0,129	0,166	0,200	0,241	0,281
		0,083	0,124	0,166	0,201	0,240	0,280
Średnie wychylenie x [m]	0,079	0,120	0,159	0,196	0,236	0,275

Równania zapisane obok każdego z wykresów to efekt wykorzystania regresji liniowej. Właśnie w tym celu wyliczyliśmy średnią wartość wychylenia dla każdego ciężaru, aby można było ujednolicić rachunki.

Regresja liniowa ma kluczowe znaczenie, ponieważ współczynnik kierunkowy a każdej z prostej, jest ściśle związany z wartością współczynnika sprężystości k sprężyn. Wyrażają to wzory:

W pierwszym równaniu wielkość x (wychylenie) ma wymiar metra, zaś wielkość Q (ciężar) ma wymiar niutona. W związku z tym współczynnik kierunkowy a, będąc odwrotnością współczynnika sprężystości, musi mieć wymiar
.
Rachunek jednostek przedstawia się następująco:

Jeśli przy pierwszej sprężynie współczynnik kierunkowy prostej wynosi 0,0677, to współczynnikiem sprężystości tej sprężyny będzie odwrotność tej liczby. Czyli mamy:

Analogicznie postępujemy z drugą prostą i drugą sprężyną:

W ten oto sposób uzyskaliśmy wartości współczynników sprężystości dwóch sprężyn, za pomocą metody statycznej.

1. Metoda dynamiczna

Aby uzyskać współczynnik sprężystości za pomocą metody dynamicznej, w pierwszej kolejności należy uśrednić pięć czasów pięćdziesięciu okresów T, a z tej średniej wyliczyć czas jednego okresu. Mając wyliczony okres T można przystąpić do wyliczenia współczynnika sprężystości, korzystając ze znanej zależności:

Uśredniamy wartości pięciu zmierzonych czasów:

Wydaje się, że można by w tym momencie przejść do wyliczenia współczynnika sprężystości, jednak nie możemy tego zrobić, ponieważ zachodzi jeszcze potrzeba wyznaczenia niepewności pomiaru czasu. Po za tym nie dokonaliśmy jeszcze analizy niepewności dla metody statycznej. Należy wiedzieć, że w obu metodach można napotkać pewne rozbieżności, które postaramy się zniwelować w następnym rozdziale.

5. Analiza niepewności
   5.1 Metoda statyczna

Wyznaczenie niepewności pomiarowych przy metodzie statycznej jest ważną częścią ćwiczenia, ponieważ w trakcie pomiarów można było spotkać się z błędem paralaksy. Po za tym, dokładność pomiarów umniejsza fakt, że nie dało się całkowicie zatrzymać ciężarka, który drgał na sprężynie. Reasumując te składniki, można założyć, że wyliczona przez nas wartość współczynnika sprężystości dla metody statycznej jest nie do końca dokładna. Aby udoskonalić obliczenia, należy przeprowadzić analizę niepewności pomiaru.
W analizie niepewności przy metodzie statycznej, można posłużyć się odchyleniem standardowym. Wielkością tą posłużymy się tutaj dwa razy. Po raz pierwszy, aby ustalić odchylenie standardowe wydłużenia sprężyny, a następnie w celu określenia zbiorczego odchylenia standardowego dla współczynnika sprężystości.
Jak napisaliśmy w pierwszym rozdziale, siłę naprężenia można wyliczyć ze wzoru:

Przekształcając powyższy wzór, otrzymamy wzór na współczynnik sprężystości:

W naszym przypadku, rolę siły naprężającej pełni siła ciężkości (masa razy przyspieszenie ziemskie), którą oznaczymy przez Q i będziemy nazywać ciężarem.

Odchylenie standardowe dla długości naciągnięcia sprężyny nr 1:

Masa [kg]	0,050	0,100	0,150	0,200	0,250	0,300
Ciężar [N]	0,490	0,980	1,470	1,960	2,450	2,940
Wychylenie [m]	0,029	0,059	0,091	0,121	0,154	0,185
		0,031	0,064	0,098	0,130	0,165	0,195
		0,031	0,064	0,101	0,130	0,163	0,196
		0,030	0,064	0,096	0,130	0,161	0,196
		0,032	0,064	0,098	0,131	0,165	0,198
		0,030	0,064	0,097	0,130	0,164	0,195
		0,031	0,063	0,099	0,129	0,162	0,200
		0,030	0,063	0,097	0,129	0,162	0,196
		0,031	0,063	0,099	0,130	0,158	0,197
		0,030	0,063	0,097	0,130	0,163	0,196
Średnie wychylenie x [m]	0,031	0,063	0,097	0,129	0,162	0,195
Odchylenie standardowe z wychylenia x	0,000849837	0,0015239	0,002626785	0,002867442	0,00340098	0,00395

Oraz nr 2:

Masa [kg]	0,025	0,050	0,075	0,100	0,125	0,150
Ciężar [N]	0,245	0,490	0,735	0,980	1,225	1,470
Wychylenie [m]	0,039	0,076	0,116	0,154	0,191	0,230
		0,083	0,122	0,162	0,201	0,240	0,281
		0,084	0,126	0,161	0,202	0,242	0,280
		0,081	0,127	0,162	0,201	0,241	0,279
		0,083	0,124	0,165	0,202	0,242	0,278
		0,085	0,125	0,163	0,200	0,239	0,279
		0,083	0,124	0,162	0,200	0,240	0,277
		0,084	0,127	0,166	0,199	0,239	0,280
		0,084	0,129	0,166	0,200	0,241	0,281
		0,083	0,124	0,166	0,201	0,240	0,280
Średnie wychylenie x [m]	0,079	0,120	0,159	0,196	0,236	0,275
Odchylenie standardowe z wychylenia x	0,014059003	0,0157282	0,015198319	0,014787382	0,015671985	0,015686

Odchylenie standardowe liczymy w następujący sposób:

=

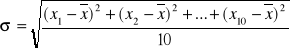
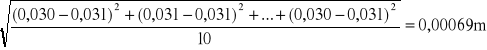
Analogicznie postępujemy dla pozostałych ciężarów oraz sprężyn.
Dla każdego ciężaru, możemy wyznaczyć współczynnik sprężystości ze wzoru podanego powyżej. Dane prezentują się następująco.

Sprężyna nr 1:

Masa [kg]	0,050	0,100	0,150	0,200	0,250	0,300
Ciężar [N]	0,490	0,980	1,470	1,960	2,450	2,940
Średnie wychylenie x [m]	0,031	0,063	0,097	0,129	0,162	0,195
Współczynnik sprężystości k [N/m]	16,06557377	15,530903	15,10791367	15,19379845	15,15151515	15,04606

Sprężyna nr 2:

Masa [kg]	0,025	0,050	0,075	0,100	0,125	0,150
Ciężar [N]	0,245	0,490	0,735	0,980	1,225	1,470
Średnie wychylenie x [m]	0,079	0,120	0,159	0,196	0,236	0,275
Współczynnik sprężystości k [N/m]	3,105196451	4,0697674	4,625550661	5	5,201698514	5,355191

Mając wyliczone współczynniki sprężystości, możemy przejść do wyznaczenia ich niepewności. Tutaj ponownie posłużymy się wielkością odchylenia standardowego.

Sprężyna nr 1

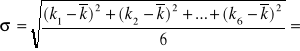
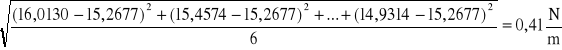
Sprężyna nr 2

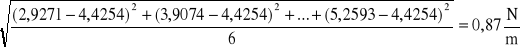
Możemy zapisać ostateczną wartość współczynników sprężystości uzyskanych metodą statyczną:

Dla sprężyny nr 1: k₁=14,77 N/m, u(k₁)=0,41 N/m
Dla sprężyny nr 2: k₂=6,30 N/m, u(k₂)=0,88 N/m

2. Metoda dynamiczna

Teraz zajmiemy się wyznaczeniem niepewności pomiarowej dla metody dynamicznej.

Należy uwzględnić niepewność standardową średniej czasów, ze względu na czas reakcji człowieka podczas zatrzymywania stopera, który wynosi u(
) = 0,20s. W związku z tym średni czas wyliczony w poprzednim rozdziale należy powiększyć właśnie o 0,20s i ostatecznie wynosi on 22,31s.

Czas przedstawiony powyżej, to czas pięćdziesięciu okresów. My musimy obliczyć czas jednego okresu, który później posłuży nam do wyznaczenia współczynnika niepewności.

W związku z tym, że reakcja człowieka bywa mniej lub bardziej opóźniona oraz że zliczanie okresów podczas drgania sprężyny mogło być w pewnym stopniu niedokładne, musimy wyznaczyć niepewność okresu T. Posłuży nam w tym celu metoda rozstępu z próby. Polega ona na tym, że należy wyliczyć różnicę pomiędzy największą, a najmniejszą wartością z zestawu danych. W naszym przypadku mamy:

Czas zmierzony [s]	okres [s]	okres max [s]	okres min [s]	rozstęp [s]
22,29	0,4458	0,4458	0,4432	0,0026
22,16	0,4432
22,2	0,444
22,19	0,4438
22,25	0,445

Ostatecznie wyliczony okres T prezentuje się następująco:

T=0,45s, u(T)=0,02s

Teraz pozostaje nam tylko wyliczyć współczynnik sprężystości z poniższej zależności:

6. Zestawienie wyników

W tym rozdziale zaprezentujemy wszystkie wyliczone wielkości w formie ostatecznej.

METODA STATYCZNA - SPRĘŻYNA NR 1
Masa [kg]	0,050	0,100	0,150	0,200	0,250	0,300
Ciężar [N]	0,49	0,98	1,47	1,96	2,45	2,94
Średnie wychylenie x [m]	0,03	0,06	0,09	0,12	0,16	0,19
Odchylenie standardowe z wychylenia x	0,00084	0,0015	0,0026	0,0028	0,0034	0,0039
Współczynnik sprężystości k [N/m]	16,065	15,53	15,10	15,19	15,15	15,04
Współczynnik sprężystości k [N/m] wyliczony z regresji liniowej wraz z niepewnością	k=14,77	u(k)=0,41
METODA STATYCZNA - SPRĘŻYNA NR 2
Masa [kg]	0,025	0,050	0,075	0,100	0,125	0,150
Ciężar [N]	0,24	0,49	0,73	0,98	1,22	1,47
Średnie wychylenie x [m]	0,08	0,12	0,15	0,19	0,23	0,27
Odchylenie standardowe z wychylenia x	0,014	0,015	0,015	0,014	0,015	0,015
Współczynnik sprężystości k [N/m]	3,10	4,06	4,62	5	5,20	5,35
Współczynnik sprężystości k [N/m] wyliczony z regresji liniowej wraz z niepewnością	k=6,30	u(k)=0,88
METODA DYNAMICZNA, MASA OBCIĄŻENIA 50g
	Czas zmierzony [s]	okres [s]	okres max [s]	okres min [s]	rozstęp [s]
	22,29	0,4458	0,4458	0,4432	0,0026
	22,16	0,4432
	22,2	0,444
	22,19	0,4438
	22,25	0,445
	Współczynnik sprężystości [N/m]	9,74

7. Wnioski

Z badań i obliczeń przez nas przeprowadzonych wynika ze:
a) Metoda dynamiczna jest skuteczniejsza i bardziej dokładna. Nie ma ryzyka popełnienia błędu paralaksy i dużo łatwiej jest dokonać analizy niepewności.

b) Pomiędzy wynikami z metody statycznej i dynamicznej są rozbieżności. Wynikają one z faktu, że w metodzie statycznej wykonanie tego ćwiczenia jest dość trudne.

c) Stabilizacja drgającej masy nie jest łatwa, ze względu na ciągłe działanie siły ciążenia, po za tym najmniejszy ruch powodował destabilizację układu.

d) Trudnością w metodzie dynamicznej może być krótki czas okresu drgań, co powoduje, że liczenie do pięćdziesięciu musi odbywać się szybko, co może spowodować pomyłkę.

---