POLITECHNIKA ŚLĄSKA W GLIWICACH

Wydział Elektryczny

Kierunek Elektronika i Telekomunikacja

Inżynierskie, niestacjonarne, zaoczne, sem. 2

LABORATORIUM Z FIZYKI

Temat ćwiczenia : Wyznaczenie prędkości dźwięku w powietrzu

Sekcja 02

Łukasz Antecki

Piotr Antończyk

Jacek Gajoch

Gliwice 2011

1. WSTĘP lub WPROWADZENIE

W fizyce fale to zaburzenia ośrodka, pola rozchodzące się w czasie i przestrzeni, przenoszące energie bez przenoszenia materii. Opis matematyczny fal to najogólniej mówiąc rozwiązanie równania falowego. Prędkość dźwięku w określonym ośrodku jest prędkością rozchodzenia się w nim zaburzenia mechanicznego. Prędkość dźwięku w powietrzu (a także ogólnie - w gazach) wyraźnie zależy od temperatury (ściślej od pierwiastka kwadratowego z temperatury wyrażonej w kelwinach). Im większa jest temperatura powietrza, tym szybciej poruszają się jego cząsteczki i tym większa jest prędkość dźwięku. W typowych warunkach, jakie spotykamy na co dzień w atmosferze ziemskiej, zmiana temperatury powietrza o 10 stopni Celsjusza spowoduje zmianę prędkości dźwięku o ok. 5 m/s. Prędkość

W powietrzu w temperaturze 15°C przy normalnym ciśnieniu prędkość rozchodzenia się dźwięku jest równa 340,3 m/s ≈ 1225 km/h. Jak już było wspomniane najważniejszym czynnikiem wpływającym na prędkość dźwięku jest temperatura, w niewielkim stopniu ma wpływ wilgotność powietrza; nie zauważa się, zgodnie z przewidywaniami modelu gazu idealnego, wpływu ciśnienia.

Doświadczalna formuła określająca zależność prędkości dźwięku w suchym (wilgotność równa zero) powietrzu dana jest przybliżonym wzorem:

V= [ 331,5 + (0,6 *@)]

gdzie:

V - prędkość dźwięku,

@ - temperatura w stopniach Celsjusza (°C).

Wzór ten jest przybliżeniem wzoru wynikającego z równania gazu doskonałego:

V= 331,5 * pierwiastek (1+ @/273,15)

Aby wyznaczyć prędkość dźwięku można zastosować jedną z kilkoma metodami m.in:

Metoda Quinckego- wyznaczanie prędkości dźwięku przy pomocy naczyń Quinckego.

Metoda Kundta - wyznaczanie prędkości dźwięku przy pomocy rury Kundta

Metoda z użyciem rury rezonansowej.

Pomiar prędkości dźwięku w powietrzu na podstawie efektu Dopplera.

Dla porównania podaje prędkość rozchodzenia się dźwięku w innych ośrodkach:

1. Rtęć - 1500 m/s

2. woda - 1500 m/s

3. lód - 3300 m/s

4. beton - 3800 m/s

5. stal - 5100 m/s - 6000 m/s

6. szkło - 6000 m/s

Podczas rozprzestrzenia się fali (tekże dźwiękowej) w ośrodkach prędkość fazowa fali może być różna dla różnych częstotliwości, mówi się wówczas, że dla tych fal zachodzi dyspersja. Dyspersję fal oraz zjawiska z niej wynikające obserwuje się w ośrodku, którego właściwości zależą od częstotliwości (długości fali)

Dyspersja jest zjawiskiem powszechnym, ulegają jej prawie wszystkie rodzaje fal w bardzo wielu ośrodkach.

2. STANOWISKO POMIAROWE

Wyposażenie Stanowiska pomiarowego:

- generator akustyczny,

- oscyloskop dwukanałowy,

- wzmacniacz,

- głośnik,

- mikrofon,

- rura z wmontowanym prętem oraz podziałką

Rys. 1. Schemat stanowiska pomiarowego

Przebieg ćwiczenia:

Układ podłączamy według przedstawionego schematu. Źródłem fali akustycznej w naszym układzie jest generator połączony z głośnikiem. Rejestracją fali dźwiękowej, zajmuje się wzmacniacz mikrofonowy. Sygnały z generatora i mikrofonu doprowadzone są bezpośrednio na wejścia oscyloskopu, odpowiednio do kanału 1 i 2. Sygnał pochodzący z mikrofonu będzie opóźniony względem sygnału z generatora o czas potrzebny na przebieg fali dźwiękowej na odcinku S między głośnikiem a mikrofonem. Na ekranie oscyloskopu obserwujemy dwa sygnały przesunięte względem siebie. Ze względu na pasmo przenoszenia wzmacniacza ważne jest uwzględnienie amplitudy obserwowanego sygnału z mikrofonu. Mierząc przesunięcie obu sygnałów w funkcji położenia mikrofonu względem głośnika wyznaczamy czas propagacji dźwięku między źródłem a odbiornikiem.

Podłączamy układ do sieci. Ustawiamy na generatorze żądaną wartość częstotliwości oraz wartość napięcia. Ważne, aby napięcie nie było za wysokie, gdyż będzie zniekształcać sygnał. Następnie musimy odpowiednio dobrać skalę pomiarową tzn., amplituda na oscyloskopie powinna mieć niewiele pełnych okresów (najlepiej 2, maks 3). Pręt powinien być maksymalnie wsunięty w rurę. Teraz gdy mamy odpowiednio dobraną skalę, możemy przełączyć oscyloskop na tryb XY czyli z odłączoną podstawą czasu. Na naszych oczach ukarze się elipsa. W tym momencie rozpoczynamy właściwe pomiary. Pręt delikatnie wyciągamy z rury obserwując jednocześnie ekran oscyloskopu. Gdy elipsa zmieni swoje położenie na prostą wtedy należy zanotować odległość. A następnie dalej wyciągamy pręt i gdy prosta przejdzie na drugą stronę układu formując się w elipsę a następnie ponownie ustabilizuje się w prostą wtedy również należy zanotować odległość odczytaną z podziałki. (Rys. Krzywych Lissajous na końcu sprawozdania.) Sytuację taką powtarzamy, aż do momentu gdy pręt będzie już maksymalnie wysunięty notując odległości przy których miało miejsce zmiana położenia prostej. Jednak dla każdej częstotliwości musimy wykonać minimum 3 pomiary. W ten sposób wykonujemy pomiary dla wszystkich żądanych częstotliwości. Mając już wszystkie wyniki pomiarowe możemy przystąpić do obliczania prędkości światła, obliczania błędów pomiarowych, rysowania wykresu a na samym końcu wyprowadzania wniosków.

3. WYNIKI POMIARÓW (BADAŃ)

Do pomiarów wybrane zostało 7 punktów pomiarowych w zakresie podanej w zadaniu częstotliwości. Punkty zostały dobrane tak, aby zaprezentować jak najszerszy zakres oraz uzyskać wysoką wiarygodność wyników. Dla każdej z częstotliwości staraliśmy się zaobserwować jak najwięcej punktów w których przesunięcie fazowe wynosiło 0 lub 180 stopni.

Seria pomiarowa polegała na ustawieniu na generatorze żądanej częstotliwości, a następnie oddalaniu mikrofonu od głośniczka do momentu, w którym na oscyloskopie pojawi się ukośna prosta kreska oznaczająca, że sygnały są przesunięte względem siebie o 0 lub 180 stopni.

Niestety na dokładność pomiarów wpływało wiele czynników. Temperatura, drgania stanowiska pomiarowego. Czynników tych nie dało się wyeliminować.

Częstotliwość fali	Odległości
600 Hz	27,5 cm, 28 cm
800 Hz	21 cm, 21.5cm
1000 Hz	17cm, 17cm, 16.5 cm
1200 Hz	14.4 cm, 14.5cm, 14.1cm, 14.5 cm
1400 Hz	11.5cm, 12.4cm, 10.9cm,13.1cm, 12.6cm,12.1cm
1600Hz	10.5cm, 10.5cm, 11cm, 11.2cm, 9.8cm, 10.6cm
1800Hz	9.4cm, 9.7cm, 9.2cm, 9.9cm, 9.4cm

4. OPRACOWANIE WYNIKÓW POMIARÓW

Obliczenie prędkości dźwięku dla poszczególnych częstotliwości (ze wzoru c=2fΔx)

Dla 600 Hz:

C1=0,275m*1200Hz=330m/s

C2=0,28m*1200Hz=336m/s

Dla 800 Hz:

C1=0,21*1600Hz=336m/s

C2=0,215m*1600Hz=344m/s

Dla 1000Hz:

C1=0,17m*2000Hz=340m/s

C2=0,17m*2000Hz=340m/s

C3=0,165m*2000Hz=330m/s

Dla 1200Hz:

C1=0.144m*2400Hz=345m/s

C2=0,145m*2400Hz=348m/s

C3=0,141m*2400Hz=338,4m/s

C4=0,145m*2400Hz=348m/s

Dla 1400Hz:

C1=0,115m*2800Hz=322m/s

C2=0,124m*2800Hz=347,2m/s

C3=0,109m*2800Hz=305,2m/s

C4=0.131m*2800Hz=366,8m/s

C5=0,126m*2800Hz=352m/s

C6=0,121m*2800Hz=338,8 m/s

Dla 1600 Hz:

C1=0,105m*3200Hz=336m/s

C2=0,105m*3200Hz=336m/s

C3=0,11m*3200Hz=352m/s

C4=0,112m*3200Hz=358,4m/s

C5=0,98m*3200Hz=313,6m/s

Dla 1800 Hz:

C1=0,94m*3600Hz=336,4m/s

C2=0,97m*3600Hz=349,2m/s

C3=0,92m*3600Hz=331,2m/s

C4=0,99m*3600Hz=356,4m/s

C5=0,94m*3600Hz=336,4m/s

5. ANALIZA DOKŁADNOŚCI (NIEPEWNOŚCI)

Błąd bezwzględny Δ=X-X0, gdzie X to wartość zmierzona, a X0 to wartość rzeczywista, która w naszym przypadku wynosi 340 m/s (według tablic) oraz wartość błędu względnego wynikającego ze wzoru δ= Δ/X0

Wagę danego błędu obliczamy ze wzoru:

Dla 600 Hz:

Δ 1=340m/s - 330m/s= 10 δ=10/340=0,0294 = 2,9% waga=0,01

Δ 2=340m/s - 336m/s= 4 δ=4/340=0,0119 = 1,2% waga=0,0625

Dla 800 Hz:

Δ 1=340m/s - 336m/s = 4 δ=4/340=0,011 = 1,1% waga=0,0625

Δ 2=340m/s - 344m/s = -4 δ=-4/340=-0,011= -1,1% waga=0,0625

Dla 1000Hz:

Δ 1=340m/s - 340m/s = 0 δ=0/340=0 waga=0

Δ 2=340m/s - 340m/s = 0 δ=0/340=0 waga=0

Δ 3=340m/s - 330m/s = 10 δ=10/340=0,0294 = 2,9% waga=0,01

Dla 1200Hz:

Δ 1=340m/s - 345m/s = -5 δ=-5/340=-0,0147=-1,47% waga=0,04

Δ 2=340m/s - 348m/s = -8 δ=-8/340=-0,0235=-2,35% waga=0,015625

Δ 3=340m/s - 338,4m/s = 1,8 δ=1,8/340=0,0052=0,52% waga=0,308642

Δ 4=340m/s - 348m/s = -8 δ=-8/340=-0,0235=-2,35% waga=0,015625

Dla 1400Hz:

Δ 1=340m/s - 322m/s = 18 δ=18/340=0,0529=5,2% waga=0,003086

Δ 2=340m/s - 347,2m/s = -7,2 δ=-7,2/340=-0,0211=-2,11% waga=0,01929

Δ 3=340m/s - 305,2m/s = 34,8 δ=34,8/340=0,1023=10,23% waga=0,000826

Δ 4=340m/s - 366,8m/s = -26,8 δ=-26,8/340=-0,0788=-7,88 waga=0,001392

5=340m/s - 352m/s = -12 δ=-12/340=-0,0352=-3,52% waga=0,006944

Δ 6=340m/s - 338,8m/s = 1,2 δ=1,2/340=-0,0352=-0,352% waga=0,694444

Dla 1600 Hz:

Δ 1=340m/s - 336m/s = 4 δ=4/340=0,011 = 1,1% waga=0,0625

Δ 2=340m/s - 336m/s = 4 δ=4/340=0,011 = 1,1% waga=0,0625

Δ 3=340m/s - 352m/s = -12 δ=-12/340=-0,0352=-3,52% waga=0,006944

Δ 4=340m/s - 358,4m/s = -18,4 δ=-18,4/340=-0,0541=-5,4% waga=0,002954

Δ 5=340m/s - 313,6m/s = 26,4 δ=26,4/340=-0,0776=7,76% waga=0,001435

Dla 1800 Hz:

Δ 1=340m/s - 336,4m/s = 3,6 δ=3,6/340=0,0105=1,05% waga=0,07716

Δ 2=340m/s - 349,2m/s = -9,2 δ=-9,2/340=-0,027=-2,7% waga=0,011815

Δ 3=340m/s - 331,2m/s = 8,8 δ=8,8/340=0,0258=2,588 waga=0,012913

Δ 4=340m/s - 356,4m/s = -16,4 δ=-16,4/340=-0,0470=-4,7% waga=0,003718

Δ 5=340m/s - 336,4m/s = 3,6 δ=3,6/340=0,0105=1,05% waga=0,07716

Błąd bezwzględny powstaje na ogół przez niedokładność przyrządu pomiarowego. W naszym przypadku niewielką rozdzielczość miała linijka używana do odczytu odległości, w której niepewność pomiaru mogła wynieść 10 mm. Do tego należy uwzględnić niepewność częstomierza wbudowanego w generator sygnału - niepewność ta, ani błąd popełniany nie jest znany w tym przypadku. Należy również wziąć pod uwagę, że linijka była zawieszona w pewnej odległości od mikrofonu i każde odchylenie kąta widzenia od 90 stopni mogło powodować błędne odczytanie wyników pomiaru-błąd paralaksy. Do wejścia oscyloskopu był podłączony także niewielki wzmacniacz. Jako iż nie były podane jego parametry takie jak pasmo przenoszenia, częstotliwości graniczne, przesunięcie fazowe jakie wprowadzał, to jego wpływ na wynik został zaniedbany (nie można odkreślić wartości o którą wynik został zafałszowany).

Stanowisko pomiarowe było niestabilne i nawet niewielkie drgania powodowały trudności w odczycie wyników z oscyloskopu oraz mogły powodować trudne do oszacowania niepewności pomiarów.

Średni błąd względy popełniany podczas pomiarów (średnia arytmetyczna) = +/- 2,99% -
pozwoli on oszacować jaki błąd procentowy popełnialiśmy (średnio) przy każdym pomiarze.

WYZNACZAMY WARTOŚĆ ŚREDNIEJ WAŻONEJ

Odchylenie standardowe liczymy ze wzoru:

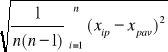
Analogicznie dla wszystkich częstotliwości. Przykładowo dla 1 KHz:

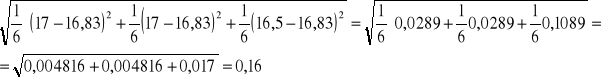
Obliczenia dla innych częstotliwości wyglądają analogicznie, więc nie będziemy ich tutaj zamieszczać.

ŚREDNIA WAŻONA:

Gdzie:

w-waga pomiaru

PN-wartość zmierzona

Korzystając z przedstawionego powyżej wzoru obliczamy średnią ważoną prędkości. Ze względu na bardzo rozbudowany sposób obliczeń przedstawiamy jedynie wynik końcowy. Średnią możemy obliczyć mając obliczone wagi dla każdego pomiaru oraz mając dane wartości prędkości każdego pomiaru. W naszym przypadku średnia ważona prędkości jest równa:

338,7433054 m/s

NIEPEWNOŚĆ POMIAROWA PRĘDKOŚCI:

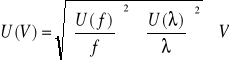
Gdzie:

U(f) - 1Hz

U(λ) - 0,01m
f- zadana częstotliwość

Λ- długość fali

V- prędkość fali dla danego pomiaru

Przedstawiamy obliczone wyniki dla każdej częstotliwości:

Dla 600 Hz

Odchylenie standardowe liczymy ze wzoru:

Średnia arytmetyczna odległości dla tego pomiaru wynosi: 27,75 cm

Średnia arytmetyczna prędkości dla tego pomiaru wynosi: 333 m/s

Odchylenie standardowe wynosi: 0,25 cm

U(v)= 6,152279

Dla 800 Hz

Średnia arytmetyczna odległości dla tego pomiaru wynosi: 21,25 cm

Średnia arytmetyczna prędkości dla tego pomiaru wynosi: 340 m/s

Odchylenie standardowe wynosi: 0,25 cm

U(v)= 8,011281

Dla 1 kHz

Średnia arytmetyczna odległości dla tego pomiaru wynosi: 16,83 cm

Średnia arytmetyczna prędkości dla tego pomiaru wynosi: 336,6 m/s

Odchylenie standardowe wynosi: 0,1666833, cm

U(v)= 10,10673

Dla 1,2 kHz

Średnia arytmetyczna odległości dla tego pomiaru wynosi: 14,37 cm

Średnia arytmetyczna prędkości dla tego pomiaru wynosi: 344,85 m/s

Odchylenie standardowe wynosi: 0,0946484 cm

U(v)= 11,83359

Dla 1,4 kHz

Średnia arytmetyczna odległości dla tego pomiaru wynosi:12,1 cm

Średnia arytmetyczna prędkości dla tego pomiaru wynosi: 338,66 m/s

Odchylenie standardowe wynosi: 0, 311448 cm

U(v)= 14,05169

Dla 1,6 kHz

Średnia arytmetyczna odległości dla tego pomiaru wynosi: 10,6 cm

Średnia arytmetyczna prędkości dla tego pomiaru wynosi: 339,2 m/s

Odchylenie standardowe wynosi: 0, 198326 cm

U(v)= 16,03914

Dla 1,8 kHz

Średnia arytmetyczna odległości dla tego pomiaru wynosi: 9,56 cm

Średnia arytmetyczna prędkości dla tego pomiaru wynosi: 341,92 m/s

Odchylenie standardowe wynosi: 0, 1256980 cm

U(v)= 17,78343

6. ZESTAWIENIE WYNIKÓW

Wykres zależności prędkości dźwięku od częstotliwości wraz z zaznaczonymi błędami.

7. PODSUMOWANIE I WNIOSKI

Biorąc pod uwagę wszystkie zebrane wyniki pomiarowe oraz obliczenia nasza grupa stwierdza że:

- badanie zostało przeprowadzone zgodnie z zaleceniami,

- przedstawione powyżej wyniki są zgodne z naszymi oczekiwaniami. Obliczone wyniki są bliskie wzorcowym wartością podanych w tablicach fizycznych( V= 340 m/s dla temp 15 stopni Celsjusza). Powstałe błędy są wynikiem błędu w odczycie, gdyż przedziałka na rurze nie była wystarczająco precyzyjna, niemożliwością ustawienia dokładnej linii prostej na wyświetlaczu oscyloskopu ze względu na ciągłe drgania stolika powodowane ruchem zarówno naszej sekcji jak i dochodzących z sąsiednich stanowisk pomiarowych. Nie bez znaczenia był także bardzo czuły wzmacniacz na wszystkie zakłócenie zewnętrzne płynące ze środowiska. Nawet niewielki dotyk oraz minimalna zmiana położenia wzmacniacza powodowała zmianę wartości podawanych na wyświetlacz oscyloskopu. Istnieje prawdopodobieństwo pojawienia się także błędów w obliczeniach. Podsumowując przedstawione błędy obliczeniowe widzimy, iż w pojedynczym przypadku błąd bezwzględny jest wyższy niż +/- 10%, dwukrotnie przekracza +/- 7%, oraz dwukrotnie +/- 5%. Wszystkie pozostałe błędy mieszczą się w przedziale od 0 - 5% przy czym większość z nich nie przekracza wartości +/- 3%. Świadczy to o przeciętnej dokładności pomiaru. Skala błędu wynika głównie z mało dokładnej skali pomiarowej na rurce. Dla przedstawionych odosobnionych przypadków mógł nastąpić zwiększony wpływ drgań oraz delikatne zmiany położenia wzmacniacza. Temperatura w chwili przeprowadzenia badania wynosiła około 15 stopni Celsjusza. W naszym przypadku możemy zacząć mówić o dyspersji, gdyż badanie choć było obarczone dużym błędem, widać na wykresie że linia powoli wznosi się do góry więc prędkość rośnie wraz z częstotliwością
. Jest to właśnie dyspersja czyli zmiana prędkości w zależności od częstotliwości. Z przeprowadzonych badań wynika też, iż Z początku krzywe Lissajous zmieniały swoje położenie co około 21 cm, zaś wraz ze wzrostem częstotliwości zwiększała się także szybkość zmian położenia krzywych i ostatecznie oscylowała w okolicy 9 cm dla ostatniego pomiaru.

---