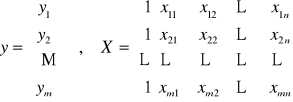
Literatura
„Ekonometria” pod redakcją M. Gruszczyńskiego, M. Podgórskiej; SGH 2002
„Ekonometria” A. Welfe; PWE 2003
„Ekonometria” W. Sadowski; WSH
„Zarys metod ekonometrii” zbiór zadań E. Nowak; PWN 1998
„Wielorównaniowe modele ekonometryczne” J. B. Gajda; PWN
„Ekonometria” G. C. Chow PWN 1995
„Econemetrics Models and Economic Forecast” R. S. Pindyck, D. L. Rubinfield; McGraw-Hill 1998
Wykład 1-2
Termin ekonometria używany jest w polskiej literaturze w dwóch znaczeniach. W szerszym znaczeniu jako zespół metod matematycznych i statystycznych stosowanych do badań ekonomicznych. W węższym znaczeniu oznacza specyficzne metody statystyczne stosowane w badaniach nieeksperymentalnych.
Ekonometria zajmuje się badaniem - mierzeniem danych ekonomicznych, badaniem obserwacji empirycznych za pomocą statystycznych metod estymacji i testowania hipotez.
Badania empiryczne i teoretyczne wzajemnie się uzupełniają. Analizy teoretyczne poddawane są weryfikacji przy pomocy danych empirycznych. Z drugiej strony do badań statystycznych potrzebne są wskazówki płynące z teorii ekonomicznych.
Podstawowym obiektem rozpatrywanym w ekonometrii jest model ekonometryczny czyli formalny zapis procesu lub zjawiska ekonomicznego. Tym formalnym zapisem jest równanie lub zespół równań wiążących rozważane zmienne.
Równanie zbudowane jest: ze zmiennych objaśnianych, objaśniających o ustalonej treści ekonomicznej; parametrów strukturalnych; składniku losowym o nieustalonej treści ekonomicznej; związku funkcyjnego łączącego te wszystkie wielkości.
Zmienna to coś co może się zmieniać, przyjmować różne wartości. Zmienne często występujące w rozważaniach ekonomicznych to: praca, zysk, koszt, dochód narodowy, import, export…
Klasyfikacja zmiennych występujących w modelu ekonometrycznym.
Ze względu na źródło zmienności:
Zmienne endogeniczne (bieżące i opóźnione, generowane od wewnątrz), zmienne określane (wyjaśniane) na podstawie modelu;
Zmienne egzogeniczne (bieżące i opóźnione, generowane z zewnątrz), wartości tych zmiennych są dane, ustalone. Zmienne nie wyjaśniane przez model.
Ze względu na rolę pełnioną przez zmienne w modelu:
Zmienne objaśniane;
Zmienne objaśniające.
Klasyfikacja modeli ekonometrycznych
Ze względu na liczbę równań
Modele jednorównaniowe
Modele wielorównaniowe
Ze względu na postać analityczną równań
Modele liniowe
Modele nieliniowe sprowadzalne do postaci liniowej - takie, które po przekształceniu przybierają postać liniową:
Modele nieliniowe i niesprowadzalne do postaci liniowej
Ze względu na rolę odgrywaną przez czas
Modele statyczne - prezentujące dane przekrojowe, dane z jednego okresu czasu
Modele dynamiczne - prezentujące zjawisko w czasie, szeregi czasowe
Model trendu
Model autoregresyjny
Ze względu na poznawcze cechy modelu.
Modele przyczynowo-skutkowe
Modele symptomatyczne
Modele trendu
Według charakteru powiązań między zmiennymi
Modele proste
Modele rekurencyjne
Modele o równaniach współzależnych.
Jeżeli za punkt odniesienia przyjmiemy cel budowy modelu to możemy wyróżnić:
Modele opisowe - budowane w celach poznawczych, głównie do celów opisowych bądź weryfikacji stawianych hipotez ekonomicznych;
Modele optymalizacyjne - klasyczne zagadnienie optymalizacji produkcji, zagadnienie diety;
Modele bilansowe - zagadnienia nakładów i wyników produkcji.
Możemy klasyfikować modele ze względu na występowanie w modelu wielkości losowej:
Modele deterministyczne - modele optymalizacyjne, modele bilansowe;
Modele stochastyczne - modele opisowe zjawisk gospodarczych.
Często stosuje się też podział modeli ze względu na zjawiska opisywane zmiennymi objaśnianymi:
Modele makroekonomiczne;
Modele mikroekonomiczne;
Branżowe
Regionalne
Gospodarki narodowej;
Handlu zagranicznego, itp…
Proces budowy modelu ekonometrycznego.
W pierwszym etapie ustalana jest mierzalna zmienna endogeniczna Y (objaśniana). Na podstawie uznawanej teorii ekonomicznej lub na podstawie zebranego materiału empirycznego formułuje się hipotezę, co do postaci modelu, zbioru zmiennych objaśniających X={X1, X2,… Xm} i zależności między zmiennymi występującymi w modelu. Tak, więc model matematyczny badanego zjawiska, czyli równanie lub układ równań wiążących rozważane przez nas zmienne są wynikiem merytorycznej analizy rozważanego zjawiska.
Zmienne mierzalne, niemierzalne, dostępne, niedostępne. Dane statystyczne: szereg czasowy, dane przekrojowe.
Przy braku teorii ekonomicznej wybieramy jako zmienne objaśniające te, które są silnie skorelowane ze zmienną objaśnianą i słabo skorelowane między sobą oraz mają związek ekonomiczny ze zmienną objaśnianą.
Y = f (X1, X2,… Xn, )
W drugim etapie zbieramy dane empiryczne, na podstawie których będziemy chcieli wyznaczyć parametry modelu i estymujemy wartości parametrów modelu.
W trzecim etapie weryfikujemy poprawność naszego modelu na podstawie nowych danych empirycznych.
W czwartym etapie stosujemy zbudowany i zweryfikowany model do celów do jakich był budowany.
Zweryfikowany model może być wykorzystywany do:
Badania ilościowych związków między badanymi zmiennymi objaśnianymi, a zmiennymi objaśniającymi;
Do prognoz;
Do poszukiwania optymalnych decyzji, itp. …
Dobór zmiennych objaśniających w modelu liniowym
Y = 0 + 1X1 + 2X2 + … + nXn +
Chcemy by zmienne objaśniające miały następujące własności:
miały wystarczająco dużą zmienność;
były silnie skorelowane ze zmienną objaśnianą;
były słabo skorelowane między sobą;
były silnie skorelowane ze zmiennymi nie występującymi w modelu, które reprezentują.
Niech y będzie wektorem obserwacji zmiennej objaśnianej, X rozszerzoną macierzą obserwacji zmiennych objaśniających X1, X2,… Xn . Dokonano m obserwacji:
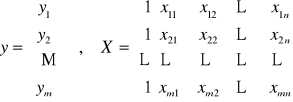
Eliminowanie zmiennych quasi-stałych
Miarą poziomu zmienności zmiennej jest następujący współczynnik zmienności:
![]()
gdzie
średnia arytmetyczna zmiennej Xi ![]()
odchylenie standardowe zmiennej Xt 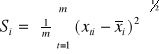
Ustalana jest pewna wartość krytyczna *. Jeśli vi ≤ v* to uznajemy zmienną za quasi-stałą i eliminujemy ze zbioru potencjalnych zmiennych objaśniających.
Przykład 1
Budujemy liniowy model ekonometryczny. Jako wartość krytyczną dla współczynnika zmienności przyjmujemy v* = 0,15.
Rok |
Y |
X1 |
X2 |
X3 |
X4 |
1993 |
12 |
6 |
11 |
5 |
35 |
1994 |
12 |
8 |
14 |
4 |
35 |
1995 |
15 |
10 |
15 |
5 |
38 |
1996 |
14 |
10 |
16 |
5 |
40 |
1997 |
16 |
8 |
18 |
4 |
41 |
1998 |
18 |
10 |
20 |
8 |
42 |
1999 |
17 |
12 |
19 |
6 |
42 |
2000 |
19 |
10 |
20 |
8 |
43 |
2001 |
20 |
12 |
15 |
7 |
44 |
2002 |
20 |
14 |
22 |
8 |
40 |
Xśri |
E(X) |
10,0 |
17,0 |
6,0 |
40,0 |
Si |
S(X) |
2,19 |
3,19 |
1,55 |
2,97 |
i |
v(X) |
0,22 |
0,19 |
0,26 |
0,07 |
Zmienna X4 jako quasi-stała musi być odrzucona.
Obliczenia do przykładu 1:
|
X4 |
X4-Xśr4 |
(X4-Xśr4)2 |
|
|
35 |
-5 |
25 |
|
|
35 |
-5 |
25 |
|
|
38 |
-2 |
4 |
|
|
40 |
0 |
0 |
|
|
41 |
1 |
1 |
|
|
42 |
2 |
4 |
|
|
42 |
2 |
4 |
|
|
43 |
3 |
9 |
|
|
44 |
4 |
16 |
|
|
40 |
0 |
0 |
|
suma |
400 |
|
88 |
|
Xśr4 |
40 |
|
8,8 |
Var(X4) |
|
|
|
2,97 |
S4 |
![]()
Wektor i macierz współczynników korelacji
Ocenę siły liniowej zależności między zmienną objaśnianą Y a zmiennymi objaśniającymi Xi dokonujemy przy pomocy współczynnika korelacji ri :
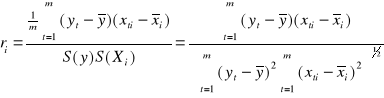
Ocenę siły liniowej zależności między zmiennymi objaśniającymi Xi Xj dokonujemy przy pomocy współczynnika korelacji rij :
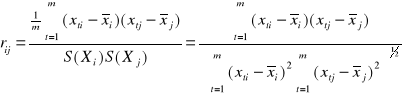
Współczynniki te przedstawiamy odpowiednio w postaci wektora i macierzy :
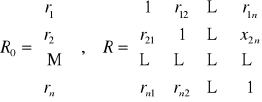
Przykład 2 (cd przykładu 1)
Obliczmy r4:
|
Y |
X4 |
Y-Yśr |
X4-Xśr4 |
(Y-Yśr)(X4-Xśr4) |
(Y-Yśr)2 |
(X4-Xśr4)2 |
|
|
|
12 |
35 |
-4,3 |
-5 |
21,5 |
18,49 |
25 |
|
|
|
12 |
35 |
-4,3 |
-5 |
21,5 |
18,49 |
25 |
|
|
|
15 |
38 |
-1,3 |
-2 |
2,6 |
1,69 |
4 |
|
|
|
14 |
40 |
-2,3 |
0 |
0 |
5,29 |
0 |
|
|
|
16 |
41 |
-0,3 |
1 |
-0,3 |
0,09 |
1 |
|
|
|
18 |
42 |
1,7 |
2 |
3,4 |
2,89 |
4 |
|
|
|
17 |
42 |
0,7 |
2 |
1,4 |
0,49 |
4 |
|
|
|
19 |
43 |
2,7 |
3 |
8,1 |
7,29 |
9 |
|
|
|
20 |
44 |
3,7 |
4 |
14,8 |
13,69 |
16 |
|
|
|
20 |
40 |
3,7 |
0 |
0 |
13,69 |
0 |
|
|
suma |
163 |
400 |
|
|
73 |
82,1 |
88 |
|
|
średnia |
16,3 |
40 |
|
|
|
|
7224,8 |
iloczyn |
|
|
|
|
|
r4 |
0,86 |
|
85,00 |
pierwiastek |
|
Obliczmy r14 :
|
X1 |
X4 |
X1-Xśr1 |
X4-Xśr4 |
(X1-Xśr1)(X4-Xśr4) |
(X1-Xśr1)2 |
(X4-Xśr4)2 |
|
6 |
35 |
-4 |
-5 |
20 |
16 |
25 |
|
8 |
35 |
-2 |
-5 |
10 |
4 |
25 |
|
10 |
38 |
0 |
-2 |
0 |
0 |
4 |
|
10 |
40 |
0 |
0 |
0 |
0 |
0 |
|
8 |
41 |
-2 |
1 |
-2 |
4 |
1 |
|
10 |
42 |
0 |
2 |
0 |
0 |
4 |
|
12 |
42 |
2 |
2 |
4 |
4 |
4 |
|
10 |
43 |
0 |
3 |
0 |
0 |
9 |
|
12 |
44 |
2 |
4 |
8 |
4 |
16 |
|
14 |
40 |
4 |
0 |
0 |
16 |
0 |
suma |
100 |
400 |
|
|
40 |
48 |
88 |
średnia |
10 |
40 |
|
|
pierwiastek |
6,93 |
9,38 |
|
|
|
|
|
|
iloczyn |
64,99 |
|
|
|
|
|
|
r14 |
0,62 |
Metoda analizy współczynników korelacji
W tej metodzie wybieramy zmienne objaśniające silnie skorelowane z ze zmienną objaśnianą, a słabo skorelowane między sobą. Do analizy używamy wektora R0 i macierzy R.
Dla danego poziomu istotności γ oraz (m-2) stopni swobody, gdzie m to ilość obserwacji wyznacza się krytyczną wartość współczynnika korelacji r* :
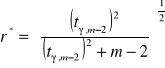
Ekonometra może sam arbitralnie ustalić wartość krytyczną r*.
Procedura ustalania zmiennych objaśniających wygląda następująco:
Ze zbioru potencjalnych zmiennych objaśniających usuwa się wszystkie dla których | ri | ≤ r* uznając, że są za mało skorelowane ze zmienną objaśnianą
Z pozostałych zmiennych wybranych do objaśniania wybieramy Xi tą, która ma największą korelację ze zmienną objaśnianą | ri | = max { |rk| ; k = 1, 2,… m}
Eliminujemy teraz wszystkie zmienne Xj, które są zbyt mocno skorelowane z wybraną zmienną Xi , tzn te dla których zachodzi |rij| > r* .
Postępowanie opisane w punktach 1, 2, 3 powtarzamy aż do wyczerpania wszystkich potencjalnych zmiennych objaśniających.
Przykład 4 (Nowak str 19)
Chcemy wyjaśnić wielkość spożycia mięsa przy pomocy z spożycia innych produktów:
Y - spożycie mięsa - zmienna objaśniana
X1 - artykuły zbożowe, X2 - ziemniaki, X3 - warzywa, X4 - owoce, X5 - tłuszcze, X6 - ryby, X7 - mleko, X8 - jajka.
Na podstawie danych statystycznych z 28 krajów obliczono odpowiednie korelacje:
|
-0,59 |
|
|
1 |
-0,09 |
0,35 |
-0,17 |
-0,26 |
-0,40 |
-0,16 |
-0,55 |
|
-0,06 |
|
|
-0,09 |
1 |
-0,06 |
-0,38 |
0,00 |
0,15 |
0,22 |
0,11 |
|
0,08 |
|
|
0,35 |
-0,06 |
1 |
0,33 |
-0,11 |
-0,20 |
-0,45 |
-0,02 |
R0 = |
0,13 |
|
R = |
-0,17 |
-0,38 |
0,33 |
1 |
0,20 |
-0,07 |
-0,44 |
0,07 |
|
0,54 |
|
|
-0,26 |
0,00 |
-0,11 |
0,20 |
1 |
0,22 |
0,17 |
-0,11 |
|
-0,15 |
|
|
-0,40 |
0,15 |
-0,20 |
-0,07 |
0,22 |
1 |
-0,19 |
0,47 |
|
-0,10 |
|
|
-0,16 |
0,22 |
-0,45 |
-0,44 |
0,17 |
-0,19 |
1 |
0,05 |
|
0,72 |
|
|
-0,55 |
0,11 |
-0,02 |
0,07 |
-0,11 |
0,47 |
0,05 |
1 |
Z tablic testu t-Studenta dla poziomu istotności γ = 0,10 oraz dla (m-2) = 26 stopni swobody odczytujemy wartość krytyczną t0,1 ; 26 = 1,706.
Następnie obliczamy wartość krytyczną współczynnika korelacji:
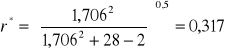
Eliminujemy najpierw wszystkie zmienne zbyt słabo skorelowane ze zmienną objaśnianą, czyli zmienne X2, X3, X4, X6, X7.
Z pozostałych wybieramy pierwszą zmienną objaśniającą czyli najsilniej skorelowaną ze zmienną objaśnianą. Wybieramy X8.
Eliminujemy teraz zmienne X zbyt silnie skorelowane ze zmienną X8 czyli spełniające |r8j|>0,317. Wyeliminowana zostaje X1. Jako druga zmienna objaśniająca zostaje przyjęta X5.
Ostatecznie przyjmujemy dwie zmienne objaśniające: X5, X8.
Y = 0 + 1X5 + 2X8 + .
Dobór zmiennych objaśniających (metoda Helwiga)
Ilość zmiennych objaśniających nie może być zbyt duża. Musimy mieć kryterium według którego będziemy je wybierać.
Przypuśćmy, że zmienne X1, X2, … Xn są kandydatkami na zmienne objaśniające. Wybierzemy te zmienne, które mają największą pojemność informacyjną.
Niech rij oznacza współczynnik korelacji liniowej Perasona między zmiennymi Xi , Xj ; rj zaś między Xj , Y.
Niech S oznacza podzbiór zbioru {1, 2, … n}
Oznaczenie
- indywidualna pojemność informacyjna nośnika Xj , j należy do S:
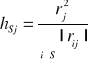
- integralna pojemność informacyjna podzbioru S:
![]()
Przykład 3
Dla zmiennej objaśnianej Y wybrano dwie zmienne objaśniające X1, X2 .
Wyliczone zostały dla nich macierze współczynników korelacji:
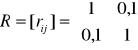
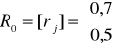
Wybrać optymalny w sensie Hellwiga zbiór zmiennych objaśniających.
H1 = h11 = 0,49 = (0,7)2/ 1 ;
H2 = h22 = 0,25 = (0,5)2/ 1 ;
h{1,2}1 = ( 0,49 ) / (1 + 0,1 ) = 0,445
h{1,2}2 = ( 0,25 ) / (1 + 0,1 ) = 0,227
H{1,2} = h{1,2}1 + h{1,2}2 = 0,672
W rozważanym przypadku optymalnym w sensie Hellwiga jest zbiór { X1 , X2 } jako zbiór objaśniający.
Wykład 3
Szacowanie parametrów modelu liniowego z jedną zmienną objaśniającą
Zajmujemy się modelem: Y = 0 + 1X + .
Chcemy oszacować parametry modelu: y^ = a0 + a1x .
Szacujemy metodą najmniejszych kwadratów, czyli chcemy minimalizować sumę kwadratów odchyleń zaobserwowanych wielkości:
et = yt - y^t , t=1, 2, … m
odchylenie wartości teoretycznej od wartości empirycznej
Minimalizujemy wielkość: e12 + e22 + … + em2 .
Czyli minimalizujemy:
(y1 - y^1)2 + (y2 - y^2)2 + … + (ym - y^m)2 .
lub
(y1 - a0 - a1x1)2 + (y2 - a0 - a1x2)2 + … + (ym - a0 - a1xm)2 .
Minimum szukamy traktując powyższe wyrażenie jako funkcję zmiennej a. Minimum funkcji jest osiągane w miejscu zerowania się pochodnej.
Równoważne wyrażenia na wartości parametrów a0, a1 :
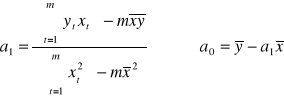
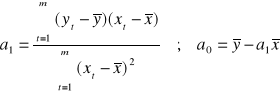
Używając zapisu wektorowego a = [a0 a1]T dostajemy:
a = (XTX)-1XTy
Ocenę wariancji Se2 oraz odchylenia standardowego Se odchyleń losowych modelu liniowego z jedną zmienną wyjaśniająca dostajemy ze wzoru:
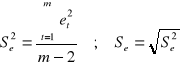
Ocenę standardowego błędu S(a0) i S(a1) oszacowania parametrów strukturalnych dostajemy ze wzorów:
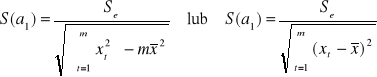
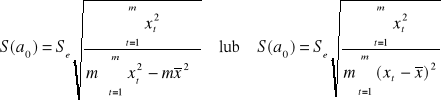
Współczynnik zbieżności 2 , determinacji R2 i współczynnik korelacji wielorakiej R
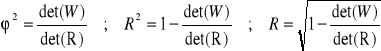
gdzie:
2 - współczynnik zbieżności, zachodzi: 0≤ 2 ≤1
R2 - współczynnik determinacji, zachodzi: 0≤ R2 ≤1
R - współczynnik korelacji wielorakiej, zachodzi: 0≤ R ≤1 ,
R - macierz współczynników korelacji zmiennych niezależnych X,
W macierz wsp. korelacji zmiennych Y, X określona następująco:
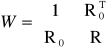
,
det(H) to wyznacznik macierzy H .
Możemy podać postać macierzy W: 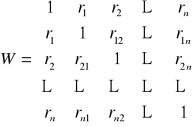
Współczynnik zbieżności 2 określa jaka część zmiennej objaśnianej jest spowodowana przez czynnik losowy.
Współczynnik determinacji R2 określa jaka część zmiennej objaśnianej jest wyjaśniona przez model.
Współczynnik korelacji wielorakiej R jest miarą związku liniowego zmiennej objaśnianej Y ze zmiennymi objaśniającymi X1 , X2 , … Xn .
Współczynnik korelacji wielorakiej może być używany do wyboru zestawu zmiennych objaśniających z zestawów o takiej samej liczności.
Przykład 1 (Nowak str 28)
Budujemy liniowy model ekonometryczny opisujący Y wartość sprzedaży przedsiębiorstwa. Zmienne objaśniające wybieramy spośród:
X1 - zatrudnienia, X2 - ilości towaru, X3 - średniej ceny, X4 - miernika wielkości przedsiębiorstwa.
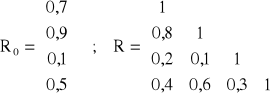
Zadanie 1: dla zmiennej objaśnianej Y i zmiennych objaśniających Y, X1, X2, X3, X4 obliczyć współczynniki:
zbieżności 2 ,
determinacji R2
korelacji wielorakiej R.

;
det(R) = 0,187; det(W) = 0,034;
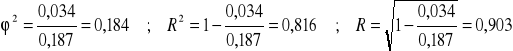
.
Zadanie 2: za pomocą współczynnika korelacji wielorakiej wybrać najlepszy zespół dwóch zmiennych objaśniających.
Ilość wszystkich dwuelementowych zbiorów zmiennych objaśniających to 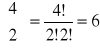
.
Wypiszmy te zbiory: {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}. Wykonajmy obliczenia współczynnika korelacji wielorakiej R{i,j} kolejno dla każdego z podzbiorów.
{1,2}: 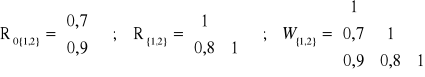
det(R{1,2}) = 1∙1 - 0,8∙0,8 = 1 - 0,640 = 0,360 ;
det(W{1,2}) = 1∙ (1∙1 - 0,8∙0,8) - 0,7∙ (0,7∙1 - 0,9∙0,8) + 0,9∙ (0,7∙0,8 - 0,9∙1) = 0,068 ;
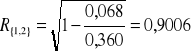
{1,3}: 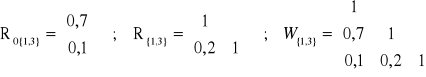
det(R{1,3}) = 1∙1 - 0,2∙0,2 = 1 - 0,040 = 0,960 ;
det(W{1,3}) = 1∙ (1∙1 - 0,2∙0,2) - 0,7∙ (0,7∙1 - 0,1∙0,2) + 0,1∙ (0,7∙0,2 - 0,1∙1) = 0,488 ;
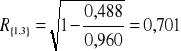
{1,4}: 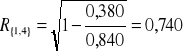
{2,3}: 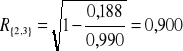
{2,4}: 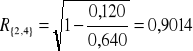
{3,4}: 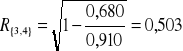
Największy współczynnik korelacji wielorakiej wynosi 0,90014 i osiągany jest dla zmiennych objaśniających X2, X4.
Wykład 4
Klasyczna metoda najmniejszych kwadratów (KMNK)
Rozważamy model liniowy:
y = 0 + 1x1 + 2x2 + … + nxn +
oraz związek między obserwacjami w modelu:
yi = 0 + 1xi1 + 2xi2 + … + nxin + i ; i = 1, 2, …, m.
lub w postaci macierzowej: Y = X + .
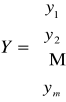
; 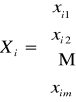
; ![]()
; 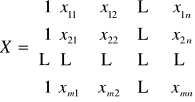
; 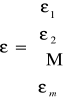
Założenia klasycznej metody najmniejszych kwadratów.
Zmienne objaśniające i składniki losowe są niezależne.
Zmienne objaśniające są nielosowe.
E(i ) = 0 , i = 1, 2, …, m - wartości oczekiwane składników losowych są równe zero.
D2(i ) = σ2 , i = 1, 2, …, m - wariancje składników losowych są równe (homoskedastyczność).
i , j są niezależne, i,j = 1, 2, …, m; j ≠ j.
i ma rozkład normalny N(0,σ2).
Liczebność próby jest większa niż liczba szacowanych parametrów, m > n+1.
Zmienne objaśniające są liniowo niezależne.
Estymacja parametrów modelu z wieloma zmiennymi objaśniającymi metodą najmniejszych kwadratów.
Podobnie jak w przypadku modelu z jedną zmienną objaśniającą, szukamy estymatorów minimalizujących sumę kwadratów odchyleń: e12 + e22 + … + em2 .
Czyli minimalizujemy:
(y1 - y^1)2 + (y2 - y^2)2 + … + (ym - y^m)2 .
lub ![]()
Podobnie jak w przypadku jednej zmiennej objaśniającej korzystamy z warunku koniecznego na minimum lokalne - zerowania się pochodnych cząstkowych:
![]()
Podobnie jak w przypadku jednej zmiennej objaśniającej obliczając pochodne dostajemy układ równań normalnych:
![]()
![]()
… …
![]()
Rozwiązując układ równań normalnych ze względu na a dostajemy w postaci macierzowej:
a = (XTX)-1XTY
Przypomnienie z zakresu algebry liniowej
Wyznacznik macierzy 2x2 det(A) = ad - bc;
|
|
a |
b |
|
A= |
|
c |
d |
|
Przykład:
det(A) = 4∙3 - 2∙5 = 12 - 10 = 2;
|
|
4 |
2 |
|
A= |
|
5 |
3 |
|
Wyznacznik macierzy nxn det(A) = a11 det(A11) - a12 det(A12) - … -+ a1n det(A1n) ;
Gdzie Aij - macierz (n-1)x(n-1) otrzymana z macierz A przez skreślenie i-tego wiersza i j-tej kolumny.
|
|
a11 |
a12 |
|
a1n |
|
A= |
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
a2n |
|
|
ann |
|
Przykład
|
|
0 |
1 |
2 |
|
A= |
|
1 |
2 |
1 |
|
|
|
2 |
1 |
0 |
|
det(A) = 0∙(2∙0 - 1∙1) - 1∙(1∙0 - 1∙2) + 2∙(1∙1 - 2∙2) = 0 + 2 - 6 = -4 .
Macierz odwrotna do macierzy A, to taka macierz A-1 , że: AA-1 = A-1A = I
Macierz odwrotna istnieje jeśli det(A) ≠ 0.
Macierz odwrotna do macierzy A-1 = [bij] gdzie bij = (+-)det(Aji)/ det(A)
Przykład
|
|
4 |
2 |
|
A= |
|
5 |
3 |
|
det(A) = 2
|
|
4 |
5 |
|
|
|
|
3/2 |
-2/2 |
|
AT = |
|
2 |
3 |
|
|
A-1 = |
|
-5/2 |
4/2 |
|
Przykład
|
|
0 |
1 |
2 |
|
A= |
|
1 |
2 |
1 |
|
|
|
2 |
1 |
0 |
|
det(A) = -4 .
|
|
0 |
1 |
2 |
|
|
|
|
0,25 |
-0,5 |
0,75 |
|
AT= |
|
1 |
2 |
1 |
|
|
A-1= |
|
-0,5 |
1 |
-0,5 |
|
|
|
2 |
1 |
0 |
|
|
|
|
0,75 |
-0,5 |
0,25 |
|
Przykład (4.1 Borkowski, Dudek, Szczesny)
Nr obserwacji |
yi |
xi1 |
xi2 |
1 |
1 |
1 |
0 |
2 |
2 |
0 |
1 |
3 |
3 |
0 |
0 |
4 |
4 |
0 |
-1 |
5 |
5 |
-1 |
1 |
6 |
6 |
1 |
-1 |
7 |
7 |
1 |
0 |
8 |
10 |
-1 |
1 |
9 |
-2 |
-1 |
-1 |
10 |
8 |
0 |
0 |
|
|
1 |
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
0 |
0 |
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Y= |
|
4 |
|
|
X= |
|
1 |
0 |
-1 |
|
|
XT= |
|
1 |
0 |
0 |
0 |
-1 |
1 |
1 |
-1 |
-1 |
0 |
|
|
|
5 |
|
|
|
|
1 |
-1 |
1 |
|
|
|
|
0 |
1 |
0 |
-1 |
1 |
-1 |
0 |
1 |
-1 |
0 |
|
|
|
6 |
|
|
|
|
1 |
1 |
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
1 |
1 |
0 |
|
|
|
|
10 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
1 |
-1 |
1 |
|
|
XTX= |
|
0 |
6 |
-2 |
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
1 |
-1 |
-1 |
|
|
|
|
0 |
-2 |
6 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ponieważ det(XTX) = 10∙(6∙6 - (-2)∙(-2)) = 10∙(36 - 4) = 320 , istnieje (XTX)-1.
|
|
0,1 |
0 |
0 |
|
|
|
|
44 |
|
|
|
|
4,40 |
|
(XTX)-1= |
|
0 |
0,1875 |
0,0625 |
|
|
XTY= |
|
1 |
|
|
(XTX)-1XTY= |
|
0,75 |
|
|
|
0 |
0,0625 |
0,1875 |
|
|
|
|
9 |
|
|
|
|
1,75 |
|
Zatem model z oszacowanymi parametrami ma postać: y^i = 4,4 + 0,75∙xi1 + 1,75∙xi2 .
Dla modelu z jedną zmienną objaśniającą wyznaczanie oszacowań parametrów strukturalnych wzorami macierzowymi i wzorami bezpośrednimi z poprzedniego wykładu daje oczywiście takie same wyniki.
Przykład (4.2 BDS)
YT= |
|
150 |
250 |
300 |
350 |
400 |
380 |
450 |
400 |
|
|
|
|
|
|
|
|
|
|
|
|
XT= |
|
200 |
300 |
400 |
400 |
500 |
500 |
600 |
700 |
|
Wyznaczyć oszacowanie parametrów modelu dwoma metodami.
Ocenę wariancji Se2 oraz odchylenia standardowego Se odchyleń losowych modelu liniowego dostajemy ze wzoru:
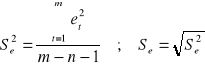
Ocenę wariancji S2(ai) oraz odchylenia standardowego S(ai) odchyleń losowych modelu liniowego dostajemy przy pomocy macierzy D2(a) wariancji i kowariancji ocen parametrów strukturalnych:
D2(a) = Se2 (XT X)-1 .
Elementy leżące na przekątnej macierzy D2(a) to oceny wariancji S2(ai) odchyleń losowych parametrów strukturalnych
Przykład 4.1 cd
Obliczenia wariancji i standardowych błędów odchyleń parametrów strukturalnych.
Nr |
yi |
xi1 |
xi2 |
y^i |
ei |
e2i |
1 |
1 |
1 |
0 |
5,15 |
-4,15 |
17,22 |
2 |
2 |
0 |
1 |
6,15 |
-4,15 |
17,22 |
3 |
3 |
0 |
0 |
4,40 |
-1,40 |
1,96 |
4 |
4 |
0 |
-1 |
2,65 |
1,35 |
1,82 |
5 |
5 |
-1 |
1 |
5,40 |
-0,40 |
0,16 |
6 |
6 |
1 |
-1 |
3,40 |
2,60 |
6,76 |
7 |
7 |
1 |
0 |
5,15 |
1,85 |
3,42 |
8 |
10 |
-1 |
1 |
5,40 |
4,60 |
21,16 |
9 |
-2 |
-1 |
-1 |
1,90 |
-3,90 |
15,21 |
10 |
8 |
0 |
0 |
4,40 |
3,60 |
12,96 |
|
|
|
|
|
suma |
97,90 |
|
|
stopni swobody |
7 |
|||
|
|
|
|
|
S2e |
13,986 |
|
|
|
|
|
Se |
3,740 |

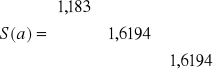
Czyli:
S(a0) =1,183 ;
S(a1) =1,619 ;
S(a2) =1,619 ;
Zatem model z oszacowanymi parametrami oraz ocenę błędów standardowych ma postać:
y^i = 4,4 + 0,75∙xi1 + 1,75∙xi2 .
y^i = |
4,4 |
+ |
0,75 |
* |
xi1 |
+ |
1,75 |
* |
xi2 |
|
(1,18) |
|
(1,62) |
|
|
|
(1,62) |
|
|
Wykład 4-5
Dopasowanie modelu do danych empirycznych
Jedna zmienna objaśniająca
Estymatory a0, a1 parametrów strukturalnych 0, 1 są zmiennymi losowymi. Przy klasycznych założeniach metody najmniejszych kwadratów estymatory te są:
liniowe ze względu zmienne zależne, ( są postaci c0 + c1y1 +…+ cmym );
nieobciążone, ( Eai = i );
efektywne, (nieobciążone z minimalną wariancją);
zgodne, (stochastycznie zbieżne do szacowanego parametru).
Liniowy model ekonometryczny to odpowiednik modelu regresji występującego w statystyce. W języku modelu regresji:
y - zmienna zależna to regresant,
x - zmienna niezależna to regresor,
1 - to współczynnik regresji.
Wykresy:
regresji w populacji E(y) = 0 + 1x (regresji I rodzaju),
regresji w próbie y^ = a0 + a1x (regresji II rodzaju).
Kryterium doboru estymatorów a0, a1 była minimalizacja kwadratów odchyleń SSE = e12+e22+…+em2. Wielkość SSE może być uznana za miarę „dopasowania” linii regresji do punktów empirycznych. Ta miara jednak ma wadę, jest zależna od użytej jednostki. Przeskalowanie zmienia jej wielkość.
Współczynnik zmienności losowej: We = Se / yśr .
Współczynnik zmienności losowej informuje jaki procent ze średniej zmiennej objaśnianej modelu stanowi odchylenie standardowe reszt. Mała wartość współczynnika We świadczy o dobrym dopasowaniu. Jaka wartość jest mała? Z góry (przed wykonaniem obliczeń) ustalamy wartość krytyczną W* współczynnika zmienności losowej. Jeśli We ≤ W* to uznajemy, że model jest dobrze dopasowany do danych empirycznych. Jeśli We > W* to uznajemy, że model nie jest dobrze dopasowany do danych empirycznych.
Dekompozycja wariancji zmiennej objaśnianej
Odchylenie zmiennej objaśnianej yi od wartości średniej yśr możemy przedstawić jako sumę odchylenia wartości teoretycznej od wartości średniej ( y^i - yśr ) i reszty ei = ( yi - y^i )
( yi - yśr ) = ( yi - y^i ) + ( y^i - yśr )
( yi - yśr ) = ( y^i - yśr ) + ei
( yi - yśr )2 = ( y^i - yśr )2 + ei2 + 2( y^i - yśr )ei
Sumę kwadratów odchyleń przedstawiamy jako:
![]()
Na podstawie założeń przyjętych w metodzie najmniejszych kwadratów, z układu równań normalnych zachodzi:
![]()
skąd ![]()
Wprowadzając oznaczenia:
![]()
Dostajemy: SST = SSR + SSE dzieląc obie strony równania przez SST dostajemy:
![]()
( SSR / SST ) = R2 nazywamy współczynnikiem determinacji,
( SSE / SST ) = 2 nazywamy współczynnikiem zbieżności,
Zachodzi: 0 ≤ R2 ≤ 1 ; 0 ≤ 2 ≤ 1 ; R2 + 2 = 1 .
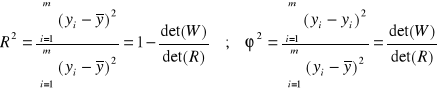
Nie można określić jaka wartość dla R2 jest dużą wartością.
Uwaga!
Współczynnik R2 można zawsze obliczyć, jednak jego interpretacja jako część wariancji zmiennej niezależnej wyjaśnionej przez wariancję zmiennej zależnej może być stosowana gdy:
zmienne x , y w populacji generalnej są powiązane liniową zależnością
parametry równania estymowane są metodą najmniejszych kwadratów
w modelu występuje wyraz wolny
Przedziały ufności
Znamy a0 , a1 oszacowania dla 0 , 1. Znamy też oszacowania wariancji S2(a0) , S2(a1).
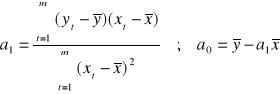
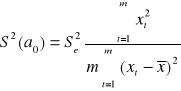
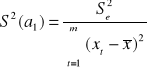
Wiemy, że ustandaryzowane zmienne losowe a0 , a1 mają rozkład t-Studenta z (m-2) stopniami swobody.
![]()
![]()
Wiemy więc również, że zachodzą nierówności:
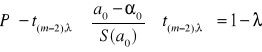
; 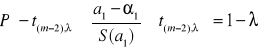
Przekształcając powyższe równania dostajemy przedziały ufności na poziomie istotności :
a0 - t(m-2), S(a0) ≤ 0 ≤ a0 + t(m-2), S(a0) ; a1 - t(m-2), S(a1) ≤ 1 ≤ a1 + t(m-2), S(a1)
Testowanie hipotez o istotności
Przy założeniach klasycznej metody najmniejszych kwadratów możemy testować, czy występuje związek między zmienną objaśnianą Y i zmienną objaśniającą X. Brak związku między zmiennymi X, Y w tym wypadku to brak zależności liniowej, czyli równość 1 = 0.
Testujemy hipotezy:
H0 : 1 = 0 ;
H1 : 1 ≠ 0 ;
Hipotezy możemy weryfikować na dwa sposoby:
Jeśli hipoteza H0 jest prawdziwa to wariancja zmiennej Y nie może być wyjaśniana przez wariancję zmiennej X zaś statystyka
![]()
ma rozkład F1,(m-2) (rozkład Fishera-Snedecora o 1 i (m-2) stopniach swobody).
Przedział ufności na poziomie istotności ma postać:
P( (R2(m-2) / (1-R2) ) ≤ F1,(m-2), ) = 1 -
Jeśli ![]()
to odrzucamy hipotezę H0.
Jeśli hipoteza H0 jest prawdziwa to statystyka
![]()
ma rozkład t-Studenta z (m-2) stopniami swobody.
Przedział ufności na poziomie istotności ma postać:
P( -t(m-2), ≤ ( a1 / S(a1) ) ≤ t(m-2), ) = 1 -
Jeśli 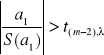
to odrzucamy hipotezę H0.
Dopasowanie modelu do danych empirycznych
Wiele zmiennych objaśniających
Estymatory a0, a1,…, an parametrów strukturalnych 0, 1,…, n są zmiennymi losowymi. Przy klasycznych założeniach metody najmniejszych kwadratów estymatory te są:
liniowe ze względu zmienne zależne, ( są postaci c0 + c1y1 +…+ cmym );
nieobciążone, ( Eai = i );
efektywne, (estymator nieobciążony z minimalną wariancją);
zgodne, ( stochastycznie zbieżny do szacowanego parametru).
Liniowy model ekonometryczny to odpowiednik modelu regresji występującego w statystyce. W języku modelu regresji:
y - zmienna zależna to regresant,
xi - zmienna niezależna to regresor,
i - to współczynnik regresji.
Kryterium doboru estymatorów a0, a1,…, an była minimalizacja kwadratów odchyleń:
SSE = e12+e22+…+em2.
y - zmienna zależna - regresant,
xi - zmienna niezależna - regresor,
i - to współczynnik regresji.
Współczynnik zmienności losowej: We = Se / yśr .
Dekompozycja wariancji zmiennej objaśnianej
Przedziały ufności
Znamy a0, a1,…, an oszacowania dla 0, 1,… n. Znamy też oszacowania wariancji S2(a0), S2(a1),…, S2(an).
Wiemy, że ustandaryzowane zmienne losowe ai mają rozkład t-Studenta z (m-n-1) stopniami swobody.
![]()
Wiemy więc również, że zachodzą nierówności:
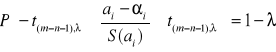
;
Przekształcając powyższe równania dostajemy przedziały ufności na poziomie istotności :
ai - t(m-n-1), S(ai) ≤ i ≤ ai + t(m-n-1), S(ai);
Testowanie hipotez
Przy założeniach klasycznej metody najmniejszych kwadratów możemy testować, czy występuje związek między zmienną objaśnianą Y i zespołem zmiennych objaśniających X1, X2,…, Xn. Brak związku między Y i wszystkimi zmiennymi X1, X2,…, Xn , czyli równość 1 = 0, 2 = 0,…, n = 0.
Testujemy hipotezy:
H0 : 1 = 2 =…=n = 0 ;
H1 : 1 ≠ 0 lub 2 ≠ 0 lub … lub n ≠ 0 .
Jeśli hipoteza H0 jest prawdziwa to statystyka
![]()
ma rozkład Fn,(m-n-1) (rozkład Fishera-Snedecora o (n) i (m-n-1) stopniach swobody).
Przedział ufności dla statystyki na poziomie istotności ma postać, F* wartość krytyczna :
P( [R2(m-n-1)] / [(1-R2)n] ) ≤ F* ) = 1 -
Jeśli ![]()
to odrzucamy hipotezę H0.
Przy założeniach klasycznej metody najmniejszych kwadratów możemy testować, czy występuje związek między zmienną objaśnianą Y i zespołem zmienną objaśniającą Xi. Brak związku między Y i zmienną Xi czyli równość i = 0.
H0 : i = 0 ;
H1 : i ≠ 0.
Jeśli hipoteza H0 jest prawdziwa to statystyka
![]()
ma rozkład t-Studenta z (m-n-1) stopniami swobody.
Przedział ufności na poziomie istotności ma postać:
P( -t(m-n-1), ≤ ( ai / S(ai) ) ≤ t(m-n-1), ) = 1 -
Jeśli 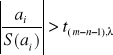
to odrzucamy hipotezę H0.
Wartość p ( p-value).
Dla ustalonej wartości w statystyki W wylicza się prawdopodobieństwo p obszaru krytycznego:
p = P( W należy do obszru krytycznego wyznaczonego przez w)
Tak wyliczoną wielkość nazywamy wartością p.
Dla ustalonej (wyliczonej) wartości F statystyki F-Fishera Snedecora z (n) i (m-n-1) stopniami swobody wylicza się prawdopodobieństwo p obszaru krytycznego wyznaczonego przez F:
p = P( Fn,(m-n-1) > F )
Tak wyliczoną wielkość nazywamy wartością p. Jeśli p < to odrzucamy hipotezę zerową H0. Jeśli p ≥ to nie ma podstaw do odrzucenia hipotezy H0.
Dla ustalonej (wyliczonej) wartości t statystyki t-Studenta z (m-n-1) stopniami swobody wylicza się prawdopodobieństwo p obszaru krytycznego wyznaczonego przez t:
p = P( |tm-n-1| > |t| )
Tak wyliczoną wielkość nazywamy wartością p. Jeśli p < to odrzucamy hipotezę zerową H0. Jeśli p ≥ to nie ma podstaw do odrzucenia hipotezy H0.
Przykład 1 (Borkowski przykład 4.12 i następne)
Zbudowany został model spożycia mięsa:
y^i = 33,22 + 0,34 xi1 - 1,90 xi2 `
gdzie:
yi - roczne spożycie mięsa wieprzowego w kg na osobę,
xi1 - roczny dochód w tys. zł na osobę,
xi2 - roczne spożycie ryb w kg na osobę,
i = 1, 2, …, 20.
|
1,11078 |
-0,02912 |
-0,04371 |
(XTX)-1 = |
-0,02912 |
0,00092 |
0,00059 |
|
-0,04371 |
0,00059 |
0,00494 |
Se = 2,85477
A więc
|
9,05252 |
-0,23730 |
-0,35622 |
D2(a) = |
-0,23730 |
0,00747 |
0,00484 |
|
-0,35622 |
0,00484 |
0,04027 |
Skąd obliczamy S(ai)
|
3,00874 |
|
|
S(a) = |
|
0,08641 |
|
|
|
|
0,20068 |
I model zapisujemy w postaci:
y^i = |
33,22 |
+ 0,34xi1 |
- 1,90xi2 |
|
[3,01] |
[0,09] |
[0,20] |
Używając statystyki F testujemy hipotezę H0 przeciwko hipotezie H1:
H0 : 1 = 2 = 0 ;
H1 : 1 ≠ 0 lub 2 ≠ 0.
|
|
df |
SS/df |
F |
p |
SSR |
1 110,48 |
2 |
555,24 |
68,13 |
7,63·10-9 |
SSE |
138,54 |
17 |
8,15 |
|
|
SST |
1 249,03 |
19 |
|
|
|
Wykonujemy jedno ze spostrzeżeń:
Wartość F* = 3,59 (odczytujemy z tablic) , a więc odrzucamy hipotezę H0 .
Wartość p < 0,05 , a więc odrzucamy hipotezę H0 .
Wartość krytyczna statystyki t-Studenta na poziomie istotności = 0,05 i dla (20-2-1) = 17 swobody wynosi t* = 2,110. Przedziały ufności dla parametrów strukturalnych są więc postaci:
0 : (33,22 - 2,110 · 3,01 , 33,22 + 2,110 · 3,01) = ( 26,87 , 39,57)
1 : (0,34 - 2,110 · 0,09 , 0,34 + 2,110 · 0,09) = ( 0,16 , 0,52)
2 : (-1,90 - 2,110 · 0,20 , -1,90 + 2,110 · 0,20) = ( -2,32 , -1,48)
Możemy więc sądzić, że z prawdopodobieństwem 0,95 :
Przedział ( 26,87 , 39,57) zawiera prawdziwą wartość 0 ;
Przedział ( 0,16 , 0,52) zawiera prawdziwą wartość 1 ;
Przedział ( -2,32 , -1,48) zawiera prawdziwą wartość 2 ;
Wyznaczamy wartości statystyki t-Studenta dla parametrów strukturalnych:
0 : t = 33,22 / 3,01 = 11,04 ; |11,04| > 2,110 ; p = 0,000000004 ;
1 : t = 0,34 / 0,09 = 3,78 ; |3,78| > 2,110 ; p = 0,001160000 ;
2 : t = -1,90 / 0,20= -9,50 ; |-9,50| > 2,110 ; p = 0,000000034 ;
Ponieważ we wszystkich przypadkach wartość bezwzględna statystyki t-Studenta jest większa od wartości krytycznej, odrzucamy hipotezę o nieistotności każdego z parametrów.
Zamiast porównywać wartość t z wartością krytyczną t* , możemy sprawdzić czy wartość p > , czyli w naszym przypadku czy p > 0,05.
Ekonometria I Eko I W1 .doc
25 / 11