1.0 Strop żelbetowy

a) rozplanowanie układu konstrukcyjnego stropu i założenia wstępne

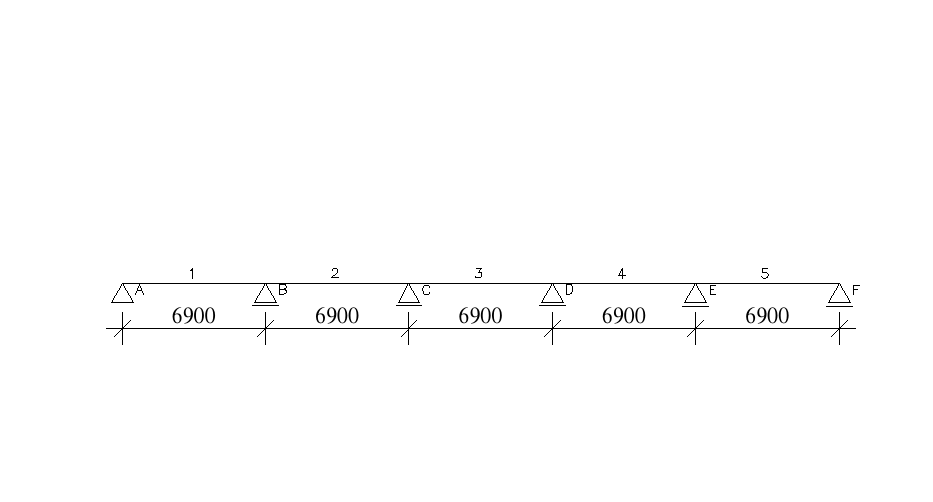
Rozstaw ram żelbetowych (rozpiętość żeber):

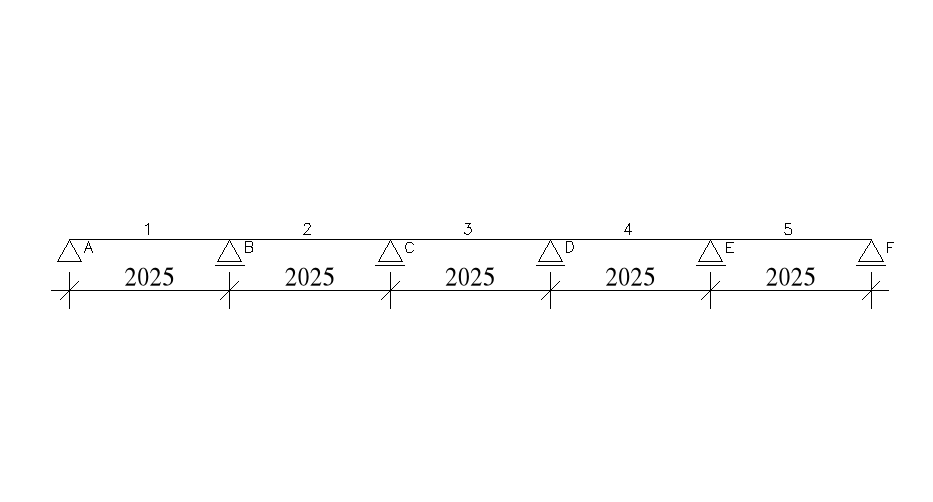
Rozstaw słupów w ramie (szerokość naw):

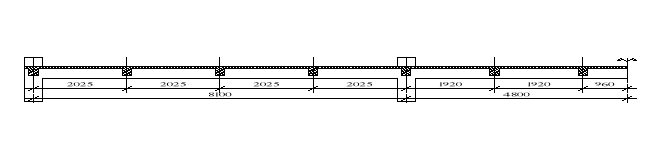
Całkowite wymiary budynku (w osiach)

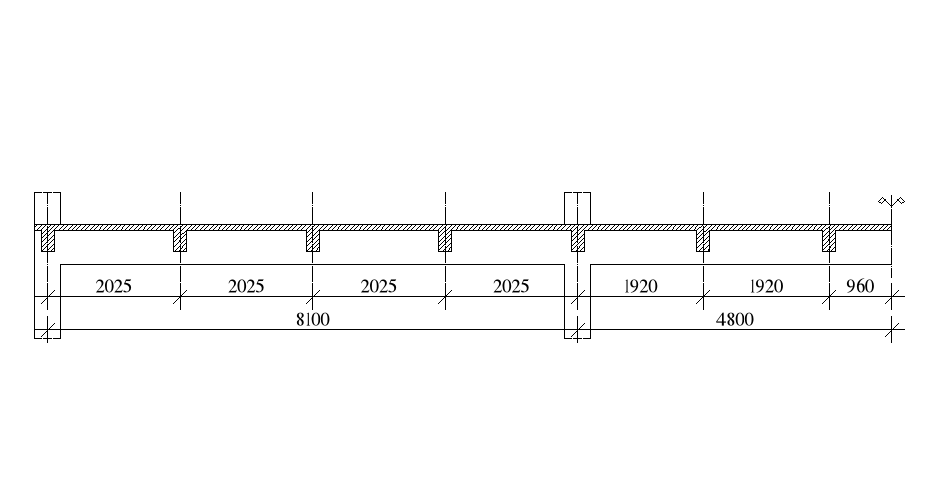
Rozpiętości płyty stropowej (rozstaw żeber):

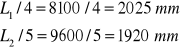
- różnica rozpiętości

Grubość płyty przyjęto wg Tabeli 3.1 (Stachurski)

b) zestawienie obciążeń stałych i zmiennych.

- obciążenia stałe:

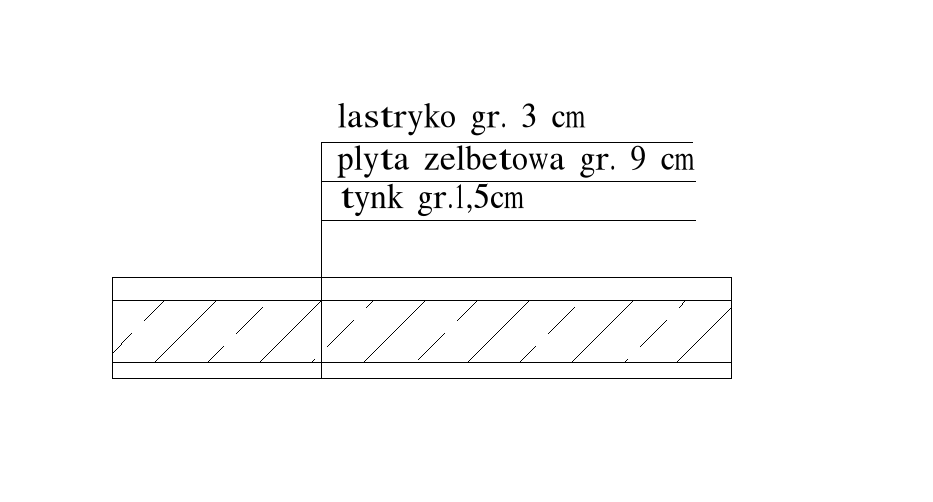
Lp.	Warstwy stropu - obciążenie	Wartość charakterystyczna kN/m	Wsp obc.	Wartość obliczeniowa kN/m
1	posadzka - lastryko gr. 3 cm 0,03 m ∙ 22,0 kN/m^3	0,66	1,3	0,86
2	płyta żelbet. monolityczna gr.9cm 0,09 m ∙ 24,0 kN/m^3	2,16	1,1	2,38
3	tynk cem.-wap. gr. 1,5 cm 0,015 m ∙ 19,0 kN/m^3	0,285	1,3	3,61
RAZEM		gk=3,10		go=3,61

- obciążenia zmienne użytkowe:

Obciążenie całkowite na 1m stropu:

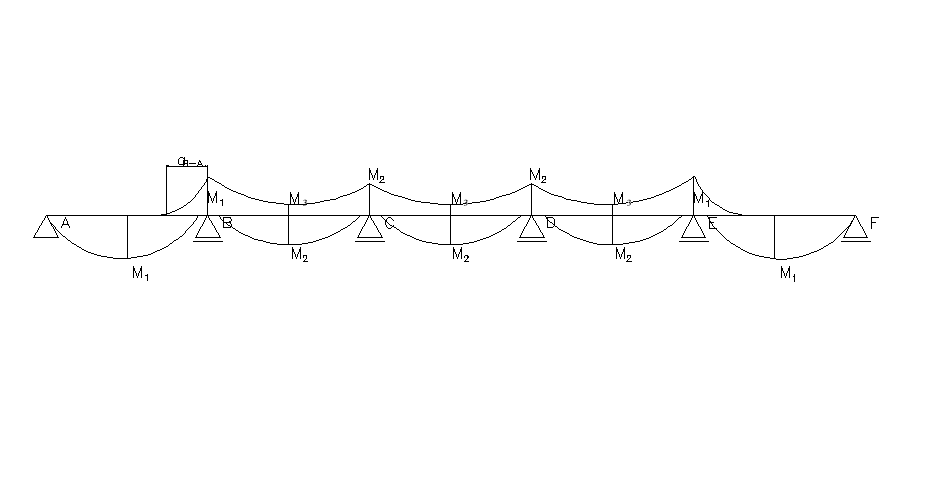
c) dobór schematu statycznego płyty stropu

przyjęto jako belkę pięcioprzęsłową:

Obliczeń dokonano metodą plastyczną wg PN-B-03264:2002

- długość efektywna

- moment w przęśle skrajnym oraz moment nad podporą przyskrajną:

- moment w przęsłach pośrednich oraz momenty na podporach pośrednich:

- wartość momentów minimalnych w przęsłach pośrednich:

obliczono zakładając obciążenie przęseł obliczonymi momentami i obciążeniem zastępczym o wartości:

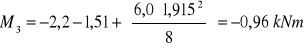
Obwiednia momentów:

Zasięg momentu ujemnego w przęśle skrajnym:

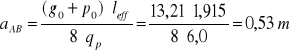
- ze względu na minimalny moment w przęśle B-C, M₃ = -0,96 kNm, należy sprawdzić, czy płyty nie trzeba zbroić górą.

cm³

gdzie:

M_cr - moment rysujący

W_c - wskaźnik wytrzymałości

b - szerokość elementu

f_ctm = 1.9, dla betonu B20

kNm

, co oznacza, że płyty nie trzeba zbroić górą.

d) wymiarowanie elementów

- grubość otulenia zbrojenia - norma PN-B-03264 „Konstrukcje betonowe, żelbetowe i sprężone”, tablica 21 dla XC1

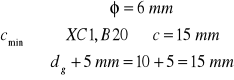
- dopuszczalna odchyłka dla elementów monolitycznych o bardzo dobrej

jakości wykonania

- przyjęta grubość płyty h = 9 cm

- beton B20 (C15/20), f_cd=10,6 MPa

- stal A-I, f_yd=210 MPa

- a₁=20+6\2=23 mm φ 6 - przyjęta średnica zbrojenia

- d=h-a₁= 90-23=67 mm - wysokość użyteczna przekroju

b=1,0 m =100 cm

α=1,0

Wymiarowanie przęsła AB (skrajnego)

dla μ=0,0925
ζ=0,943 ξ<0,25

zbrojenie w przęśle AB:

Wymiarowanie przęsła BC (pośredniego)

dla μ=0,0637
ζ=0,956 ξ<0,25

zbrojenie w przęśle BC (pośrednim):

Dobór zbrojenia w poszczególnych przęsłach:

- w przęśle BC itd.

przyjęto pręty φ6 co 12,0 cm o A=2,36 cm²- w tym co drugi pręt odgięty nad podporę

- w przęśle AB (skrajnym)

przyjęto pręty φ6 co 12,0 cm o A=2,36 cm² - w tym co drugi pręt odgięty nad podporę

+ pręt φ6 co 24 cm o A=1,18 cm² - odgięty nad podporę pośrednią i prosty na podporze skrajnej A

co daje:

- w przęśle AB - A_s= 2,36 + 1,18 = 3,54 cm² > A_s1 = 3,316 cm²

- nad podporą B - A_s= 2,36/2 + 2,36/2 + 1,18 = 3,54 > A_s1 = 3,316 cm²

- w przęśle BC i kolejnych - A_s=2,36 cm² > A_s1 = 2,253 cm²

- nad podporą C i kolejnych - A_s=2,36/2 + 2,36/2 = 2,36 cm² > A_s1 = 2,253 cm²

Sprawdzenie nośności przekroju płyty na ścinanie (siły porzeczne)

gdzie:

b_w = 1,00 m

d = 0,067 m

σ_cp = (N_sd+N_pd)/A_s = 0 - nie występują siły podłużne ani sprężające

f_ctd = 0,87 MPa = 870 kPa - dla betonu B20

k = 1 - mniej niż połowa prętów doprowadzona do podpory jako pręty proste

< 0,01

Nośność przekroju na ścinanie:

Siła poprzeczna :

V_sd = 14,46 kN < V_Rd1 = 28,54 kN - nośność została zachowana

2.0. Żebro stropu

a) wstępne przyjęcie wymiarów przekroju poprzecznego żebra (PN-B-03264)

wysokość żebra:

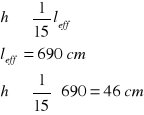
przyjęto h_ż = 50 cm

szerokość żebra:

przyjęto b_w = 20 cm

b) zestawienie obciążeń z poz. 1.0

- obciążenia charakterystyczne stałe:

- obciążenia zmienne

- obciążenia obliczeniowe stałe

Zestawienie obciążeń dla żebra stropowego

- charakterystyczne

stałe :

zmienne :

- obliczeniowe

stałe :

zmienne :

c) obliczenia statyczne

Belki ciągłe sztywno połączone na podporach można obliczać jak belki ciągłe podparte przegubowo.

Do obliczeń przyjęto belkę pięcioprzęsłową

jak na schemacie:

d) przyjęcie efektywnej szerokości półki b_eff w przekroju teowym

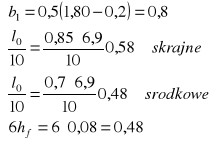
l_o - odległość obliczeniowa pomiędzy zerowymi wartościami momentów zginających, przyjęte według schematu rys. 8 (norma, strona 22, 23)

l_o - dla przęsła pierwszego: l_o = 0.85l₁

l_o - dla przęsła drugiego: l_o = 0.7l₂

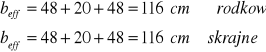
e) wymiarowanie przekrojów

- grubość otulenia zbrojenia

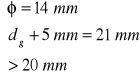
dopuszczalna odchyłka

- odległość między warstwami prętów:

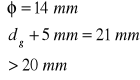
- sprawdzenie czy przekrój należy obliczać jako pozornie teowy czy rzeczywiście teowy

- przekrój pozornie teowy

- przekrój rzeczywiście teowy

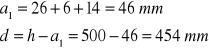
Wymiarowanie przęsła pierwszego:

dla

- przekrój pozornie teowy

przyjęto 5φ14 o A_s1 = 7,70 cm²

Wymiarowanie przęsła drugiego:

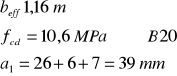
d = h - a₁ =500-39 = 461mm

(zakładam że zbrojenie w jednym rzędzie)

dla

- przekrój pozornie teowy

przyjęto 4φ14 o A_s1 = 6,16 cm²

Wymiarowanie przęsła trzeciego:

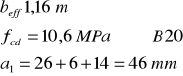
d = h - a₁ =500-46 = 454mm

(zakładam że zbrojenie w jednym rzędzie)

dla

- przekrój pozornie teowy

przyjęto 4φ14 o A_s1 = 6,16cm²

Wymiarowanie przekrojów podporowych:

- podpora B:

Na osi:

M
)

α₁ = 1-

L₁ - rozpiętość żebra z jednej strony podpory L₁=L₂

L₁ = 690 cm

b - szerokość podparcia

b = 40 cm

α₁ = 1-

α₂ = 1-

α₂ = 1-

L₂ - rozpiętość żebra z drugiej strony podpory

L₂ = 690 cm

M
) = 0.5∙140,365∙ (1+0.95∙0.95) = 133,52 kNm

dla

przyjęto 6φ14 o A_s1 = 9,24 cm²

- podpora C:

Na osi:

M
) = 0.5∙122,490∙ (1+0.95∙0.95) = 116,52 kNm

dla

przyjęto 5φ14 o A_s1 = 7,70 cm²

Wymiarowanie przekrojów podporowych na krawędziach podpór (rygli)

Obliczenie momentów krawędziowych:

Obliczanie sił poprzecznych - tablice Winklera

• Obliczanie M_BL

q_o + p_o = 8,86+16,85 = 25,71 kN/m∙0.20 = 5,142 kN

Q_BL = 109,042 kN

M_BL = -140,365 - (5,142∙0.20∙0.5) + 109,042∙0,2 = -119,07 kN

• Obliczanie M_BP

q_o + p_o = 8,86+16,85 = 25,71 kN/m∙0.20 = 5,142 kN

Q_BP = 101,713 kN

M_BP = -140,365 - (5,142∙0.20∙0.5) + 101,713∙0,2 = -120,536kN

• Obliczanie M_CL

q_o + p_o = 8,86+16,85 = 25,71 kN/m∙0.20 = 5,142 kN

Q_CL = 95,998 kN

M_CL = -122,490 - (5,142∙0.20∙0.5) + 95,998∙0,2 = -103,8 kN

• Obliczanie M_CP

q_o + p_o = 8,86+16,85 = 25,71 kN/m∙0.20 = 5,142 kN

Q_CP = 99,268 kN

M_CP = -122,49 - (5,142∙0.20∙0.5) + 99,268∙0,2 = -103,15 kN

Obliczenie potrzebnego zbrojenia na krawędziach podpór dla przekroju prostokątnego z założonym zbrojeniem ściskanym

- podpora B

h = 50 cm

b = 20cm

A_S2 = 2 ∅ 14 = 3,08 cm²

A_S1 = A_S1'+ A_S1”

A_S1 - zbrojenie szukane

A_S1”= A_S2 = 3,08 cm²

ΔM = A_S2 ∙ f_yd ∙ (h-a₁ - a₂)

ΔM = 3,08∙35∙ (50-3,9-3,9) = 4549 kNcm = 45,5 kN/m

Do obliczenia A_S1 potrzebne jest wyznaczenie współczynnika μ według wzoru:

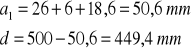
μ =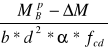

μ =

według tablicy 3.4. (A. Łapko „Projektowanie konstrukcji żelbetowych”)

dla μ = 0,174 ζ = 0,900

A_S1^' =

A_S1 = 5,30 cm² + 3,08 cm² = 8,38cm²

Przyjęto 6∅14 mm o A_s1 = 9,24 cm²

- podpora C

h = 50 cm

b = 20cm

A_S2 = 2 ∅ 14 = 3,08 cm²

A_S1 = A_S1'+ A_S1”

A_S1 - zbrojenie szukane

A_S1”= A_S2 = 3,08 cm²

ΔM = A_S2 ∙ f_yd ∙ (h-a₁ - a₂)

ΔM = 3,08∙35∙ (50-3,9-3,9) = 4549 kNcm = 45,5 kN/m

Do obliczenia A_S1 potrzebne jest wyznaczenie współczynnika μ według wzoru:

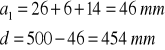
μ =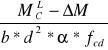

μ =
0

według tablicy 3.4. (A. Łapko „Projektowanie konstrukcji żelbetowych”)

dla μ = 0,133 ζ = 0,923

A_S1^' =

A_S1 = 3,97 cm² + 3,08 cm² = 7,05 cm²

Przyjęto 5∅14 mm o A_s1 = 7,70 cm²

Obliczenie nośności.

1. Nośność w przęśle A-B.

Nośność w przęśle A-B obliczono ze względu największą wartość momentu w przęsłach.

Żebro w przęśle jest elementem pojedynczo zbrojonym. Nośność elementu pojedynczo zbrojonego określamy z poniższego wzoru:

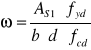
gdzie:

A_s1 = 7,70 cm² dla 5 prętów φ 14mm

f_yd = 350 Mpa,

b = 116 cm,

d = 500 -46 = 454mm

f_cd = 10,6 Mpa

Nośność graniczną można wyznaczyć ze wzoru:

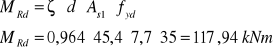
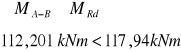
Powyższy warunek na nośność został spełniony.

2. Nośność w przęśle B-C.

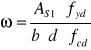
gdzie:

A_s1 = 6,16 cm² dla 4 prętów φ 14mm

f_yd = 350 Mpa,

b = 116 cm,

d = 500 -39 = 461mm

f_cd = 10,6 Mpa

Nośność graniczną można wyznaczyć ze wzoru:

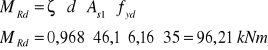
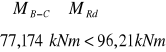
Powyższy warunek na nośność został spełniony.

3. Nośność w przęśle C-D.

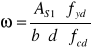
gdzie:

A_s1 = 6,16 cm² dla 4 prętów φ 14mm

f_yd = 350 Mpa,

b = 116 cm,

d = 500 - 39= 461 mm

f_yd = 10,6 Mpa

Nośność graniczną można wyznaczyć ze wzoru:

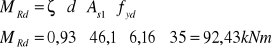
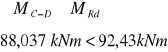
Powyższy warunek na nośność został spełniony

4. Nośność w podporze B.

Nośność w podporze B obliczono ze względu największą wartość momentu w podporze.

Żebro w podporze jest elementem pojedynczo zbrojonym. Nośność elementu pojedynczo zbrojonego określamy z poniższego wzoru:

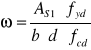
gdzie:

A_s1 = 9,24 cm² dla 6 prętów φ 14mm

f_yd = 350 Mpa,

b = 20 cm,

d = 567-50,6 = 516,4mm

f_yd = 10,6 Mpa

Nośność graniczną można wyznaczyć ze wzoru:

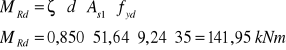
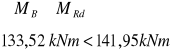
Powyższy warunek na nośność został spełniony.

5. Nośność w podporze C.

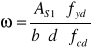
gdzie:

A_s1 = 7,7 cm² dla 5 prętów φ 14mm

f_yd = 350 Mpa,

b = 20 cm,

d = 566,7 - 46 = 520,7 mm

f_yd = 10,6 Mpa

Nośność graniczną można wyznaczyć ze wzoru:

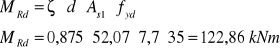
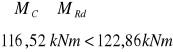
Powyższy warunek na nośność został spełniony.

OBLICZENIE ZBROJE NIA NA ŚCINANIE

(wg PN-B-03264, punkt 5.53)

Obliczenie zbrojenia przy podporze A (stan graniczny nośności - ścinanie)

Przyjęto strzemiona ze stali A-0, o średnicy ∅6 mm

Q
76,147 kN

f_ctd = 0,87 kN/cm - dla betonu klasy B20

b_w = 20 cm

g_o= 8,86 kN/m

p_o= 16,85 kN/m

Obliczenie siły V_sd:

V_sd = Q_A - (g_o + p_o ) ∙ 0,20

V_sd = 76,147 - (8,86 + 16,85) ∙ 0.20 = 71,005 kN

Obliczenie siły V_Rd1:

V_Rd1 =
(wg PN-B-03264 wzór 67)

ρ_L =
=0.50%

V_Rd1 =
= 44,77 kN

z = 0.9 ∙ d = 41,49

V_sd = 71,005 kN> V_Rd1 = 44,77 kN

(wg PN-B-03264 wzór 72)

Ponieważ V_Rd1 < V_Sd < V_Rd2

Niezbędne jest wyznaczenie ilości zbrojenia na ścinanie na odcinku:

m

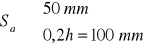
- przyjęto S_a = 50 mm

- przyjęto S_b = 80 mm

Projektowanie strzemion:

Strzemiona ze stali A0, o średnicy ∅6 mm

A_Sw1 = 0,57 cm² dla 2 prętów φ6

ctgθ=1,6

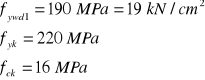
zakładamy że

Obliczenie

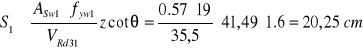
przyjęto S₁=20 cm

Projektowanie prętów odgiętych:

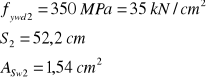
Obliczenie

V_Rd32=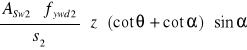

V_Rd32=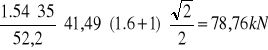

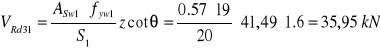
Obliczenie siły V_Rd3

Obliczenie zbrojenia z lewej strony podpory B (stan graniczny nośności - ścinanie)

Przyjęto strzemiona ze stali A-0, o średnicy ∅6 mm

Obliczenie siły V_sd:

V_sd = Q_BL - (g_o + p_o ) ∙ 0.20

V_sd = 109,042 - (8,86 + 16,85) ∙ 0.20 = 103,9 kN

Obliczenie siły V_Rd1:

V_Rd1 =

ρ_L =
=1,05%

V_Rd1 =
= 50,63

z = 0,9 ∙ d = 39,96 cm

V_sd = 103,9 kN> V_Rd1 = 50,63 kN

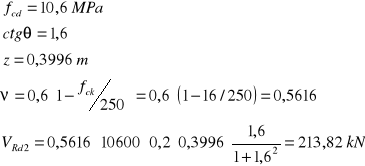
Ponieważ V_Rd1 < V_Sd < V_Rd2

Niezbędne jest wyznaczenie ilości zbrojenia na ścinanie na odcinku:

m

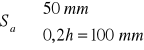
- przyjęto S_a = 50 mm

- przyjęto S_b = 80 mm

Projektowanie strzemion:

Strzemiona ze stali A0, o średnicy ∅6 mm

A_Sw1 = 0,57 cm² dla 2 prętów φ6

ctgθ=1,6

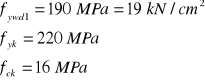
zakładamy że

Obliczenie

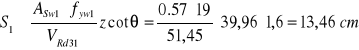
przyjęto S₁=13 cm

Projektowanie prętów odgiętych:

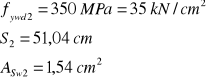
Obliczenie

V_Rd32=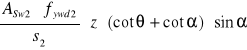

V_Rd32=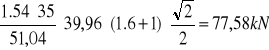

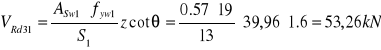
Obliczenie siły V_Rd3

Obliczenie zbrojenia z prawej strony podpory B (stan graniczny nośności - ścinanie)

Przyjęto strzemiona ze stali A-0, o średnicy ∅6 mm

Obliczenie siły V_sd:

V_sd = Q_BP - (g_o + p_o ) ∙ 0.20

V_sd = 101,713 - (8,86 + 16,85) ∙ 0.20 = 96,571kN

Obliczenie siły V_Rd1:

V_Rd1 =

ρ_L =
=1,05%

V_Rd1 =
= 50,63

z = 0,9 ∙ d = 39,96 cm

V_sd = 96,571 kN> V_Rd1 = 50,63 kN

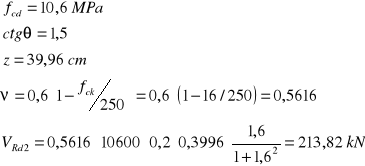
Ponieważ V_Rd1 < V_Sd < V_Rd2

Niezbędne jest wyznaczenie ilości zbrojenia na ścinanie na odcinku:

m

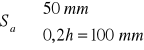
- przyjęto S_a = 50 mm

- przyjęto S_b = 80 mm

Projektowanie strzemion:

Strzemiona ze stali A0, o średnicy ∅6 mm

A_Sw1 = 0,57 cm² dla 2 prętów φ6

ctgθ=1,6

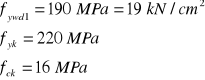
zakładamy że

Obliczenie

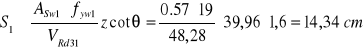
przyjęto S₁=14 cm

Projektowanie prętów odgiętych:

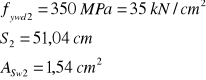
Obliczenie

V_Rd32=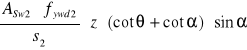

V_Rd32=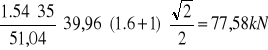

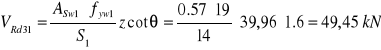
Obliczenie siły V_Rd3

Obliczenie zbrojenia z lewej strony podpory C (stan graniczny nośności - ścinanie)

Przyjęto strzemiona ze stali A-0, o średnicy ∅6 mm

Obliczenie siły V_sd:

V_sd = Q_CL - (g_o + p_o ) ∙ 0.20

V_sd = 95,998 - (8,86 + 16,85) ∙ 0.20 = 90,85 kN

Obliczenie siły V_Rd1:

V_Rd1 =

ρ_L =
=0,85%

V_Rd1 =
= 48,79 kN

z = 0,9 ∙ d = 40,86 cm

V_sd = 90,85kN> V_Rd1 = 48,79kN

Ponieważ V_Rd1 < V_Sd < V_Rd2

Niezbędne jest wyznaczenie ilości zbrojenia na ścinanie na odcinku:

m

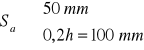
- przyjęto S_a = 50 mm

- przyjęto S_b = 80 mm

Projektowanie strzemion:

Strzemiona ze stali A0, o średnicy ∅6 mm

A_Sw1 = 0,57 cm² dla 2 prętów φ6

ctgθ=1,6

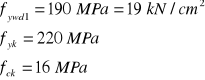
zakładamy że

Obliczenie

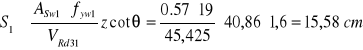
przyjęto S₁=15 cm

Projektowanie prętów odgiętych:

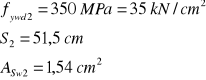
Obliczenie

V_Rd32=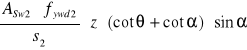

V_Rd32=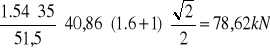

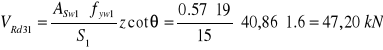
Obliczenie siły V_Rd3

Obliczenie zbrojenia z prawej strony podpory C (stan graniczny nośności - ścinanie)

Przyjęto strzemiona ze stali A-0, o średnicy ∅6 mm

Obliczenie siły V_sd:

V_sd = Q_CP - (g_o + p_o ) ∙ 0.20

V_sd = 99,268 - (8,86 + 16,85) ∙ 0.20 = 94,126 kN

Obliczenie siły V_Rd1:

V_Rd1 =

ρ_L =
=0,85%

V_Rd1 =
= 48,79 kN

z = 0,9 ∙ d = 40,86 cm

V_sd = 94,126kN> V_Rd1 = 48,79 kN

Ponieważ V_Rd1 < V_Sd < V_Rd2

Niezbędne jest wyznaczenie ilości zbrojenia na ścinanie na odcinku:

m

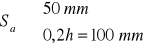
- przyjęto S_a = 50 mm

- przyjęto S_b = 80 mm

Projektowanie strzemion:

Strzemiona ze stali A0, o średnicy ∅6 mm

A_Sw1 = 0,57 cm² dla 2 prętów φ6

ctgθ=1,6

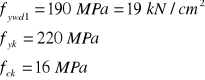
zakładamy że

Obliczenie

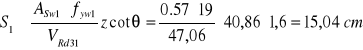
przyjęto S₁=15 cm

Projektowanie prętów odgiętych:

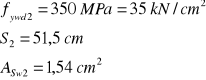
Obliczenie

V_Rd32=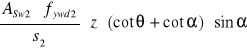

V_Rd32=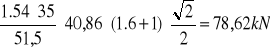

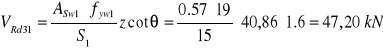
Obliczenie siły V_Rd3

Obliczanie szerokości rysy przęsła skrajnego - metoda dokładna

Szerokość rys prostopadłych do osi belki obliczymy ze wzoru:

gdzie:

β - współczynnik wyrażający stosunek obliczeniowej szerokości rysy do szerokości średniej; β = 1.7

S_rm - średni końcowy rozstaw rys

gdzie:

k₁ - współczynnik zależny od przyczepności prętów - dla prętów żebrowanych = 0.8

k₂ - współczynnik zależny od rozkładu odkształceń rozciąganych - przy zginaniu = 0.5

ρ_r - efektywny stopień zbrojenia

ostatecznie

ε_sm - średnie odkształcenie zbrojenia rozciąganego

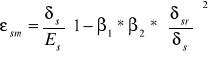
δ_s - naprężenie w zbrojeniu rozciąganym

E_s - moduł sprężystości stali = 200GPa = 200000MPa

β₁ - współczynnik zależny od przyczepności prętów , równy 1 dla prętów żebrowanych

β₁ - współczynnik zależny od czasu działania i powtarzalności obciążenia , równy 0.5 dla obciążeń długotrwałych

We wzorach zamiast stosunku
można przyjąć stosunek

Moment rysujący oblicza się ze wzoru:

gdzie:

f_ctm - średnia wytrzymałość betonu na rozciąganie, dla betonu B20 - f_ctm= 1.9 MPa

Przy obliczaniu momentu bezwładności i wskaźnika wytrzymałości należy obliczyć współczynnik α_e,t uwzględniający wpływ pełzania betonu przy obciążeniach długotrwałych

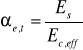
E_c,eff - efektywny moduł sprężystości betonu obliczamy ze wzoru:

gdzie:

E_cm - średni sieczny moduł sprężystości betonu dla B=20 E_cm = 29.0GPa

φ(t,t₀) - końcowy współczynnik pełzania betonu, wyznaczony z tablicy 3 PN-B-03264

Obliczam miarodajny wymiar przekroju elementu, potrzebny do wyznaczenia φ(t,t₀)

gdzie:

A_c- pole przekroju elementu [mm²]

U- obwód przekroju poddany działaniu powietrza [mm]

dla h₀=111,89mm wg PN-B-03264 tab. A.1 φ(∞,t₀)= 3,32→β_c(t-t₀)=0,439 dla obciążenia po 28 dniach, stąd φ(t,t₀)=1,457

Przyjmując, że element będzie obciążony po 28 dniach otrzymujemy:

ostatecznie

Obliczenie środka ciężkości

Obliczenie momentu bezwładności i wskaźnika wytrzymałości:

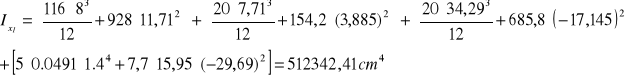
Obliczenie momentu rysującego:

Obliczenie naprężeń w zbrojeniu belki:

Obciążenia stałe charakterystyczne:

q_k = 7,66 kN/m²

Obciążenia zmienne charakterystyczne:

p_k = 14,04 ∙ 0,8=11,232 kN/m²

Stopień zbrojenia rozciąganego:

Ponieważ ρ_l = 0,84% to ξ = 0,85 na podstawie tab. D-1 PN.

ostatecznie ε_sm wynosi

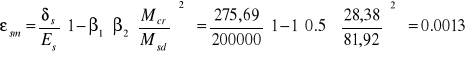
Szerokość rys prostopadłych do osi belki wynosi:

Obliczenie ugięcia przęsła skrajnego metodą dokładną

Ugięcia elementów o stałym przekroju i obciążeniu długotrwałym można obliczyć ze wzoru:

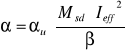
gdzie

α_u - współczynnik zależny od rozkładu mementu zginającego

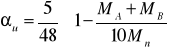
gdzie:

M_A - moment na podporze A

M_A = 0

M_B - moment na podporze B; wynosi

M_B = ( -0.105 ∙ 7,66 -0.119 ∙11,232) ∙ 6.9²=-101,93kNm

M_m - moment w środku rozpiętości żebra

M_m =( 0.078 ∙ 7,66 + 0.100 ∙ 11,232) ∙ 6.9² = 81,92 kNm

Ostatecznie:

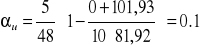
l_eff - rozpiętość efektywna żebra,

l_eff = 690cm

M_sd = maksymalny moment zginający wywołany maksymalnym obciążeniem

M_sd = 81,92kNm

β - sztywność przekroju, w którym osiąga się moment M_sd można obliczyć ze wzoru:

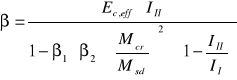
gdzie:

E_c,eff - efektywny moduł sprężystości betonu,

E_c,eff = 11,80 [GPa] = 1180[kN/cm²]

M_cr - moment rysujący,

M_cr = 28,38 kNm

β₁ - współczynnik zależny od przyczepności prętów, równy 1 dla żebrowanych

β₂ - współczynnik zależny od czasu działania i powtarzalności obciążenia, równy 0.5 dla obciążeń długotrwałych

I_I - moment bezwładności przekroju po wystąpieniu rys

Obliczenie wielkości statycznej w fazie II - [x_II]

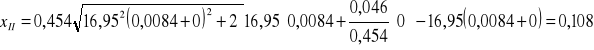
=10,8

Moment bezwładności przekroju zarysowanego:

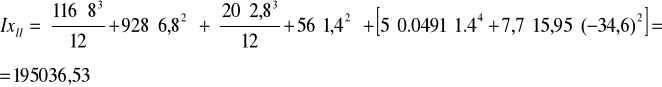
ostatecznie:

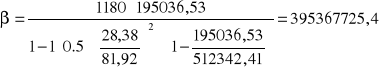
Ostatecznie ugięcie wynosi:

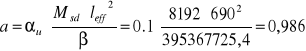
cm

Ugięcie graniczne wynosi:

a = 0,986 cm < a_lim = 3.3cm - warunek spełniony

Obliczanie rys w pozostałych przęsłach

- metoda uproszczona

Przęsło B-C

Szerokość rys prostopadłych w elementach zginanych o przekroju prostokątnym określono na podstawie zależności:

tab. D-1 PN.

Ponieważ ρ_l = 0,66% to ξ = 0,85 na podstawie tab. D-1 PN.

Na podstawie określonych wyżej danych z tab. D-1 PN (po interpolacji) ustalono że maksymalna średnica pręta jest równa 27mm

Na podstawie powyższej nierówności można przyjąć że szerokość rys jest ograniczona do w_lim = 0,30mm

Przęsło C - D

Szerokość rys prostopadłych w elementach zginanych o przekroju prostokątnym określono na podstawie zależności:

tab. D-1 PN.

Ponieważ ρ_l = 0,84% to ξ = 0,85 na podstawie tab. D-1 PN.

Na podstawie określonych wyżej danych z tab. D-1 PN (po interpolacji) ustalono że maksymalna średnica pręta jest równa 32mm

Na podstawie powyższej nierówności można przyjąć że szerokość rys jest ograniczona do w_lim = 0,30mm

Obliczanie ugięcia w POZOSTAŁYCH przęsłch

- metoda uproszczona

Sprawdzenie ugięcia polega na spełnieniu warunku

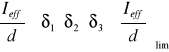
gdzie

(l_eff/d)_lim - podstawowa wartość graniczna ugięcia określana wskaźnikiem sztywności jest wyznaczona z tablicy 15 normy PN-B-03264 (przy określaniu tego parametru należy posłużyć się obliczeniami wykonanymi przy obliczeniu rys metodą uproszczoną)

δ₁-δ₃ - współczynniki korekcyjne dla wartości podstawowej wskaźnika sztywności

d - wysokość użyteczna przekroju

1. Przęsło drugie B-C

Dane :

h = 500mm

b = 200mm

l_eff = 6,9m

stal klasy A -III

4 pręty φ 14mm (A_s1 = 6,16cm²)

beton klasy B-20

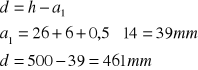
Stopień zbrojenia rozciąganego:

Po interpolacji z tabl. 13 dla wewnętrznego przęsła belki ciągłej(beton klasy B-20, stopień zbrojenia 0,66%) odczytujemy:

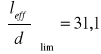
Powyższa wartość musi być skorygowana współczynnikami
.

Dla elementów o rozpiętości l_eff >6m wartość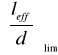
wymnażamy przez:

a_lim - wartość graniczna ugięcia określoną w tablicy 8 dla odpowiedniej rozpiętości l_eff [mm].

a_lim = 30mm

Naprężenia σ_s w zbrojeniu rozciąganym

Obciążenia stałe charakterystyczne:

q_k = 7,66 kN/m²

Obciążenia zmienne charakterystyczne:

p_k = 14,04×0,8=11,232 kN/m²

Ponieważ ρ_l = 0,66% to ξ = 0,85 na podstawie tab. D-1 PN.

Ponieważ maksymalne wartości stosunku l_eff/d wyznaczono dla σ_s = 250 MPa to pozostałe wartości należy pomnożyć przez 250/σ_s

Współczynnik δ₃ przyjmuje równy 1, ponieważ belka pracuje jako wolnopodparta.

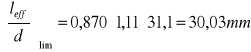
Warunek stanu granicznego ugięcia jest spełniony, ponieważ:

2. Przęsło trzecie C - D

Dane :

h = 500mm

b = 200mm

l_eff = 6,9m

stal klasy A -III

5 prętów φ 14mm (A_s1 = 7,70cm²)

beton klasy B-20

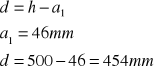
Stopień zbrojenia rozciąganego:

Po interpolacji z tabl. 13 dla wewnętrznego przęsła belki ciągłej(beton klasy B-20, stopień zbrojenia 0,84 %) odczytujemy:

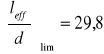
Powyższa wartość musi być skorygowana współczynnikami
.

Dla elementów o rozpiętości l_eff >6m wartość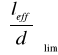
wymnażamy przez:

a_lim - wartość graniczna ugięcia określoną w tablicy 8 dla odpowiedniej rozpiętości l_eff [mm].

a_lim = 30mm

Naprężenia σ_s w zbrojeniu rozciąganym

Obciążenia stałe charakterystyczne:

q_k = 7,66 kN/m²

Obciążenia zmienne charakterystyczne:

p_k = 14,04×0,8=11,232 kN/m²

Ponieważ ρ_l = 0,84% to ξ = 0,85 na podstawie tab. D-1 PN.

Ponieważ maksymalne wartości stosunku l_eff/d wyznaczono dla σ_s = 250 MPa to pozostałe wartości należy pomnożyć przez 250/σ_s

Współczynnik δ₃ przyjmuje równy 1, ponieważ belka pracuje jako wolnopodparta.

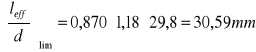
Warunek stanu granicznego ugięcia jest spełniony, ponieważ:

Katedra Konstrukcji Betonowych i Murowych PB WBiIŚ

PROJEKT Z KONSTRUKCJI ŻELBETOWYCH PŁYTA STROPOWA, ŻEBRO

Str. - 1 -

20

8

50

l₀ = 0.7l₂

l₀ = 0.85l₁

l₂

l₁

q = 9,86+16,85 kN/m

M = 140,365kNm

Q
=109,042 kN

q = 25,71 [kN/m]

M = 140,365 kNm

Q
= 101,713 kN

M = 122,490 kNm

q = 25,71 kN/m

Q
=95,998 kN

q = 25,71 [kN/m]

M = 122,49 kNm

Q
= 99,268 kN

116

•

• • • •

---