GRAWITACJA - Ie

Pocisk

Pocisk o masie m = 1 kg został wystrzelony z powierzchni Ziemi pionowo do góry z prędkością o wartości równej drugiej prędkości kosmicznej v_II. Przyjmujemy, że war­tość przyspieszenia g = 9,81
, promień Ziemi R = 6370 km.

1. Na jakiej wysokości h nad Ziemią mógłby znajdować się taki punkt A, w którym
   wartość prędkości pocisku byłaby równa wartości pierwszej prędkości kosmicz­nej v_I wyznaczonej dla odległości równej promieniowi Ziemi R?

2. Oblicz wartość energii kinetycznej E_k pocisku w punkcie A.

3. W jakiej odległości h₁ od powierzchni Ziemi pocisk miał energię kinetyczną o i mniejszą od energii kinetycznej początkowej?

4. Oblicz wartość siły grawitacji działającej na ciało o masie m = 1 kg umieszczone w odległości h₁ od powierzchni Ziemi.

5. Znajdź odległość r < R od środka Ziemi takiego punktu B, w którym wektor siły grawitacji był taki sam jak w punkcie odległym o h₁ od powierzchni Ziemi.

6. W jakim czasie ciało puszczone swobodnie z punktu znajdującego się w odległo­ści h₁ od powierzchni Ziemi przebędzie drogę długości x - 1 m? Zakładamy, że na drodze długości 1 m nie występuje zmiana wartości przyspieszenia.

Rzut pionowy

Ciało o masie m = 1 kg zostało wyrzucone z powierzchni Ziemi pionowo w górę z prędkością o wartości v = 1
. W obliczeniach przyjmij g = 9,81
.

1. Oblicz wartość siły grawitacji F działającej na ciało w najwyższym punkcie A to­ru jego ruchu, czyli w odległości r_A od środka Ziemi.

2. Oblicz wartość pracy W, jaką wykonała siła grawitacji F, przemieszczając ciało
   z punktu A do środka Ziemi.

3. Podaj zależność siły grawitacji
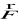
   od odległości r od środka Ziemi i przedstaw wykres siły grawitacji F działającej na ciało dla odległości r
   (0, r_A).

4. Podaj wartość prędkości v₁, jaką należałoby nadać ciału, aby poruszało się po or­bicie o promieniu r_A.

5. Zapisz wzory na obliczanie energii potencjalnej E_p, kinetycznej E_k i całkowitej E_c
   w zależności od odległości r od środka Ziemi satelity o masie m = 1 kg porusza­jącego się po orbicie. Wiadomo, że odległość r jest większa od promienia Ziemi R.

6. Przedstaw w jednym układzie współrzędnych wykresy zależności energii poten­cjalnej E_p , energii kinetycznej E_k, energii całkowitej E_c satelity od odległości r.

Tunel

Ciało o masie m - 5 kg puszczono swobodnie do tunelu przewierconego wzdłuż śred­nicy Ziemi. Odległość r ciała od środka Ziemi jest mniejsza od promienia Ziemi R.

1. Napisz równanie opisujące wartość siły F działającej na ciało o masie m = 5 kg
   w zależności od odległości r od środka Ziemi i uzasadnij odpowiedź na pytanie:
   jakim ruchem poruszało się to ciało?

2. Napisz równanie ruchu ciała i narysuj wykres zależności odległości r od czasu t.

3. Podaj równanie opisujące zależność wartości prędkości v ciała od czasu t i oblicz
   maksymalną wartość v_max

4. Napisz równanie zależności przyspieszenia a tego ciała od odległości r i oblicz
   wartość maksymalną przyspieszenia a_max.

5. Wskaż punkty, w których wartości energii potencjalnej E_p ciała i kinetycznej E_k są
   maksymalne. Napisz równania maksymalnej energii potencjalnej E_pmax maksy­malnej energii kinetycznej E_kmax Oblicz wartość energii całkowitej ciała E_c.

6. Z jakiej wysokości h nad powierzchnią Ziemi należałoby puścić swobodnie ciało o masie m, aby jego prędkość na powierzchni Ziemi była równa maksymalnej prędkości ciała poruszającego się w tunelu?

Satelita

Ciało o masie m = 100 kg porusza się po orbicie na wysokości h = 160 km nad powierzchnią Ziemi. Promień Ziemi R = 6370 km, wartość przyspieszenia g = 9,81
.

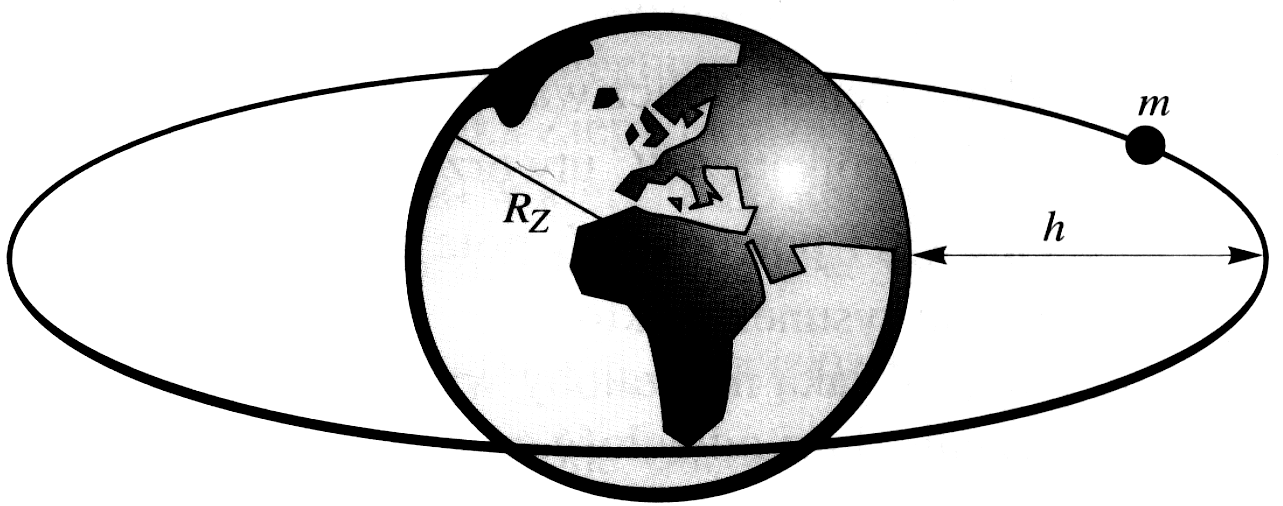
1. Oblicz wartość prędkości v₁ ciała.

2. Jaką pracę W należałoby wykonać, aby przenieść ciało z orbity znajdującej się na wysokości h nad powierzchnią Ziemi na orbitę znajdującą się na wysokości h_{ = 300 km od powierzchni Ziemi?

3. Podaj zależność okresu T₁, obiegu satelity na orbicie bliższej i okresu T₂ obiegu satelity na orbicie dalszej.

4. Jaką pracę W₁ należałoby wykonać nad ciałem poruszającym się po orbicie w od­ległości h = 160 km od powierzchni Ziemi, aby opuściło pole grawitacyjne Ziemi?

Superpozycja

W punktach K i L oddalonych od siebie o 2r znajdują się punktowe masy m_K = m i m_L=10m.

a)Wyznacz, korzystając z rysunku, natężenie pola grawitacyjnego γ_A, γ_B, γ_c w punktach A, B, C.

b)Wyznacz położenie punktu X leżącego na prostej przechodzącej przez środki ciał, w którym natężenie pola grawitacyjnego pochodzącego od ciał o masach m_K, m_L jest równa zeru.

c)Gdzie na linii łączącej ciała K i L należy umieścić trzecią masę punktową m_Y= 2m, aby ciało o masie m_K pozostało w spoczynku?

d)Zakładamy, że ciała o masach m_K i m_L zaczęły się poruszać pod wpływem
działania sił wzajemnego oddziaływania grawitacyjnego. Wyznacz stosunek wartości ich przyspieszeń w chwili, gdy zaczynają się poruszać.

Superpozycja II

Trzy jednakowe planety: 1, 2, 3 o promieniach R = 3000 km są położone tak, że ich środki wyznaczają wierzchołki trójkąta równobocznego ABC o boku długości a = 2R. Gęstość każdej planety jest taka sama i wynosi ρ = 5 · 10³

1. Wykonaj rysunek układu planet. Oblicz wartość natężenia
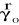
   i potencjał V_o pola grawitacyjnego w środku trójkąta ABC utworzonego przez środki planet.

2. Jakie będzie natężenie
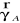
   i potencjał V_A pola grawitacyjnego w środku jednej z trzech planet? Wykonaj rysunek wektorów.

3. Oblicz całkowitą pracę W, jaką należałoby wykonać, aby planetę 2. i planetę 3. odsunąć na nieskończenie dużą odległość od planety 1.

Ciekawa grawitacja

W ołowianej kuli o gęstości ρ = 11,3 · 10³
i promieniu R = 100 cm jest zrobione

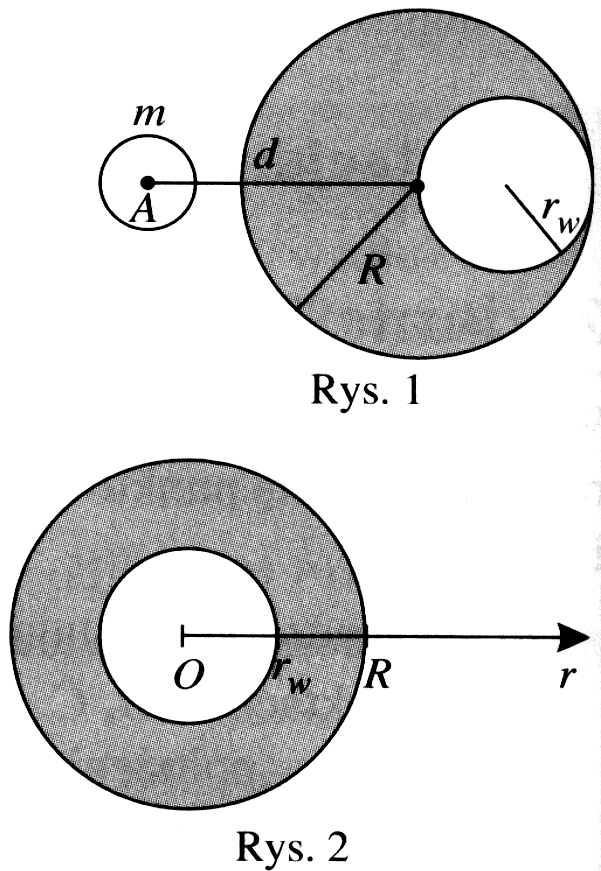
kuliste wydrążenie o promieniu r_w = 50 cm.

1. Powierzchnia wydrążenia jest styczna do powierzch­ni kuli (rys. 1). W punkcie A, który znajduje się w odległości d = 150 cm od środka ołowianej kuli, umieszczono kulkę o masie m = 100 g. Środki ołowianej kuli, wydrążenia i kulki o masie m leżą na jednej prostej. Jaką siłą F ołowiana kula przy­ ciąga kulkę o masie ml

2. Środek kulistego wydrążenia pokrywa się z środ­kiem ołowianej kuli (rys. 2). Wyznacz, a następnie narysuj wykres zależności wartości natężenia pola grawitacyjnego γ kuli z wydrążeniem od odległości rod jej środka.

c) Wartość potencjału grawitacyjnego w środku jednorodnej kuli bez wydrążenia wynosi
, gdzie M oznacza masę ołowianej kuli, R promień kuli. Wykaż, że praca
potrzebna do przeniesienia ciała o masie m z środka kuli na jej powierzchnię jest dwukrotnie mniejsza niż praca
potrzebna do przeniesienia tego ciała z powierzchni kuli do nieskończoności.

Satelita geostacjonarny

Wszystkie ciała fizyczne na Ziemi poruszają się po orbitach kołowych. Przyczyną tego zjawiska jest obrót Ziemi dookoła własnej osi. Powoduje on między innymi odchylanie toru ruchu spadających ciał na wschód, odchylanie toru ruchu pocisków artyleryjskich w płaszczyźnie poziomej w kierunku prostopadłym do południka ziemskiego, różnicę między ciężarem ciał na równiku i na biegunie.

1. W jakiej odległości rod środka Ziemi okrążają satelita geostacjonarny?

2. Pocisk wystrzelono poziomo w kierunku południka ziemskiego. Wystrzał nastą­pił na szerokości geograficznej północnej φ= 55° z lufy skierowanej na połud­nie. Wartość prędkości początkowej v pocisku była równa 800
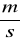
   . Opór powie­trza zaniedbujemy. W którą stronę odchyli się tor lotu pocisku od kierunku południka? W jakiej odległości ∆s od południka znajduje się pocisk po 1 s lotu?

3. Jaki musiałby być okres T₁ obrotu Ziemi wokół własnej osi, aby na równiku przyspieszenie ziemskie było równe zeru? Przyjmujemy, że promień Ziemi R₁ = 6378 km.

4. Stosunek ciężaru ciała umieszczonego na równiku pewnej planety do ciężaru ciała, gdy znajduje się na biegunie, jest równy
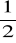
   . Gęstość planety wynosi ρ = 3 · 10³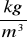
   . Wyznacz okres T_p obrotu planety dookoła własnej osi. Promienie równikowy i biegunowy są sobie równe.

Ziemia - Księżyc

Masa Ziemi M_Z jest 81 razy większa od masy Księżyca M_K= 7,34 · 10²² kg. Promień Ziemi R_z = 6370 km jest 3,7 razy dłuższy od promienia Księżyca R_K. Średnia odległość środka Księżyca od środka Ziemi wynosi d= 3,84 · 10⁸ m.

1. W jakiej odległości x od środka Ziemi, na linii łączącej środki ciał, znajduje się taki punkt A, w którym na ciało o masie m = 100 kg nie działa siła grawitacji.

2. Porównaj wartość siły grawitacji F_x działającej na ciało o masie m = 100 kg znaj­dujące się na powierzchni Ziemi z siłą F_Y działającą na to ciało, gdy znajduje się
   ono na powierzchni Księżyca.

3. Naszkicuj wykres zależności siły grawitacji
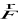
   działającej na ciało o masie m w zależności od odległości r od środka Ziemi, dla r
   d. Uzasadnij kształt wykresu.

4. Oblicz energię kinetyczną E_k, potencjalną E_p i całkowitą E_c Księżyca w polu grawitacyjnym Ziemi.

5. Jaką pracę W należałoby wykonać, aby przenieść Księżyc z orbity okołoziemskiej do nieskończoności?

Prawa Keplera

W centralnym polu grawitacyjnym ciało porusza się po jednej z krzywych stożkowych. Jeżeli energia mechaniczna ciała jest ujemna, tor ruchu ciała ma kształt okręgu lub elipsy. Jeżeli energia mechaniczna ciała jest równa zeru, tor ruchu ciała ma kształt paraboli. Jeżeli energia mechaniczna ciała jest dodatnia, tor ruchu ciała ma kształt hiperboli.

Gdy tor ruchu planety ma kształt elipsy, to w jednym z ognisk znajduje się Słońce. Podobnie satelity ziemskie poruszają się po torach w kształcie okręgu lub elipsy, a w ognisku znajduje się Ziemia (rysunek).

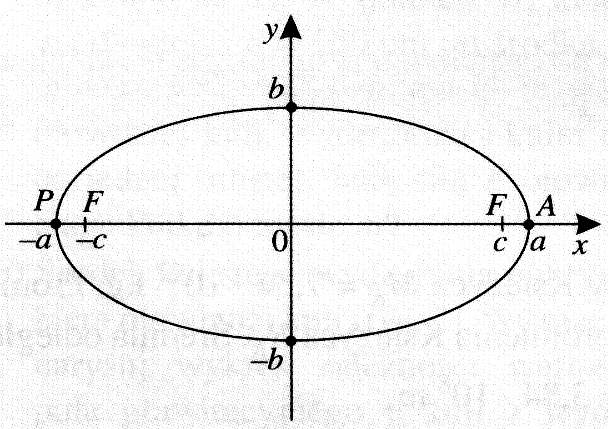
a, b - długości wielkiej i małej półosi elipsy

P - peryhelium (perygeum) - najbliższe

położenie Słońca (Ziemi)

A — aphelium (apogeum) — najdalsze

położenie Słońca (Ziemi)

F — ognisko

c — ogniskowa; c =

e - mimośród; e =

S = πab - pole powierzchni ograniczonej elipsą

W ruchu satelitów obowiązuje zasada zachowania momentu pędu L

(
), z której wynika stałość prędkości polowej v_p planety (v_p =
, gdzie dS oznacza wycinek pola zakreślony przez promień wodzący planety). Stały jest również stosunek
, gdzie T oznacza okres

obiegu planety wokół Słońca, M_S - masę Słońca, m_p - masę planety.

Wykorzystaj podane informacje do rozwiązania zadań.

1. Wyznacz wartość średniej prędkości v Ziemi w jej ruchu obiegowym dookoła Słońca. Załóż kołowy kształt orbity. Przyjmij średnią wartość promienia orbity okołosłonecznej r= 149,6 · 10⁶km.

2. Oblicz wartość średniej prędkości polowej Ziemi v_p. Przyjmij wartość długości półosi elipsy: a = 149 598 500 km, b = 149 479 000 km.

3. Dwie planety obiegają Słońce po orbitach kołowych o promieniach r₁ i r₂. Wyznacz stosunek wartości prędkości liniowych v₁ do v₂ tych planet w ruchu wokół Słońca.

4. Sputnik krąży wokół Ziemi po orbicie eliptycznej o mimośrodzie e. Wyznacz stosunek wartości prędkości liniowych
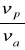
   , gdzie v_p oznacza prędkość w perygeum, a v_a w apogeum.

e) Wyznacz okres obiegu T_S satelity Ziemi, wiedząc, że odległość satelity w apo­geum R_a=8R_Z, a w perygeum R_p = 2R_Z, gdzie promień Ziemi R_Z = 6370 km, masa Ziemi M_Z = 6 · 10²⁴ kg. Przyjmij, że masa satelity m_S « M_Z.

f) Stosunek odległości R_p (w perygeum) do odległości R_a (w apogeum) wynosi
. Oblicz stosunek wartości prędkości liniowych
w perygeum i apogeum.

g) Dwie gwiazdy każda o masie M znajdują się w odległości d od siebie i poruszają się po tej samej orbicie dookoła wspólnego środka masy O. Wyznacz zależność wartości prędkości liniowej v w ruchu po orbicie i okresu obiegu T_g od ich wzajemnej odległości d.

---