Zadanie 1
Na podstawie Rocznika Statystycznego dobierz dwie serie danych do analizy poziomu średniego zmiennych, rozrzutu względem średniej oraz liniowej zależności jednej zmiennej od drugiej. Dane powinny być zebrane z minimum 20 okresów (stanów zmiennej). Dokonaj wizualizacji danych oraz przedstaw wyniki analiz w postaci wykresów.
Dobór danych.
Dane, które wybrałam do analizy jednej zmiennej od drugiej pochodzą z rządowej strony internetowej Głównego Urzędu Statystycznego ( www.stat.gov.pl), załączonej poniżej . Dane pochodzą z lat 1997-2001. Dotyczą one wskaźników makroekonomicznych gospodarki Polski. Jedna seria danych przedstawia przeciętne miesięczne wynagrodzenie realne brutto w gospodarce narodowej ogółem (X), druga zaś sprzedaż produkcji budowlano-montażowej ogółem niewyrównana sezonowo (ceny stałe) (Y).
Zebrane przeze mnie dane przedstawia poniższa tabela:
|
|
|
|
DANE |
|
|
Okresy |
|
lata |
kwartały |
Miesięczne wynagrodzenie |
Sprzedaż produkcji budowlano- montażowej |
|
|
|
|
|
X |
Y |
|
1 |
|
|
I |
102 |
123,5 |
|
2 |
|
1997 |
II |
105,9 |
125,2 |
|
3 |
|
|
III |
105,8 |
121,1 |
|
4 |
|
|
IV |
105,7 |
119,4 |
|
5 |
|
|
I |
104,8 |
125,4 |
|
6 |
|
1998 |
II |
103,4 |
117 |
|
7 |
|
|
III |
103,9 |
114,9 |
|
8 |
|
|
IV |
103,9 |
111,6 |
|
9 |
|
|
I |
102,4 |
99,2 |
|
10 |
|
1999 |
II |
103,8 |
101,8 |
|
11 |
|
|
III |
104,2 |
102,7 |
|
12 |
|
|
IV |
103,1 |
103,2 |
|
13 |
|
|
I |
104,7 |
99,2 |
|
14 |
|
2000 |
II |
102,4 |
101,8 |
|
15 |
|
|
III |
100,5 |
102,7 |
|
16 |
|
|
IV |
101,4 |
103,2 |
|
17 |
|
|
I |
102,5 |
99,2 |
|
18 |
|
2001 |
II |
100,8 |
91,5 |
|
19 |
|
|
III |
102,5 |
90,6 |
|
20 |
|
|
IV |
101,3 |
89,6 |
|
1. Obliczenia.
Wyniki obliczeń z przeprowadzonej analizy powyższych danych umieściłam w poniższej tabelce:
OBLICZENIA |
|||||||||
|
|
|
|
|
|
|
|
|
|
t |
X |
Y |
X-Xsr |
Y-Ysr |
|X-Xsr| |
|Y-Ysr| |
(X-Xsr)2 |
(Y-Ysr)2 |
(X-Xsr)(Y-Ysr) |
1 |
102 |
123,5 |
-1,250 |
16,360 |
1,250 |
16,360 |
1,563 |
267,650 |
-20,450 |
2 |
105,9 |
125,2 |
2,650 |
18,060 |
2,650 |
18,060 |
7,023 |
326,164 |
47,859 |
3 |
105,8 |
121,1 |
2,550 |
13,960 |
2,550 |
13,960 |
6,502 |
194,882 |
35,598 |
4 |
105,7 |
119,4 |
2,450 |
12,260 |
2,450 |
12,260 |
6,003 |
150,308 |
30,037 |
5 |
104,8 |
125,4 |
1,550 |
18,260 |
1,550 |
18,260 |
2,402 |
333,428 |
28,303 |
6 |
103,4 |
117 |
0,150 |
9,860 |
0,150 |
9,860 |
0,023 |
97,220 |
1,479 |
7 |
103,9 |
114,9 |
0,650 |
7,760 |
0,650 |
7,760 |
0,423 |
60,218 |
5,044 |
8 |
103,9 |
111,6 |
0,650 |
4,460 |
0,650 |
4,460 |
0,423 |
19,892 |
2,899 |
9 |
102,4 |
99,2 |
-0,850 |
-7,940 |
0,850 |
7,940 |
0,722 |
63,044 |
6,749 |
10 |
103,8 |
101,8 |
0,550 |
-5,340 |
0,550 |
5,340 |
0,302 |
28,516 |
-2,937 |
11 |
104,2 |
102,7 |
0,950 |
-4,440 |
0,950 |
4,440 |
0,903 |
19,714 |
-4,218 |
12 |
103,1 |
103,2 |
-0,150 |
-3,940 |
0,150 |
3,940 |
0,023 |
15,524 |
0,591 |
13 |
104,7 |
99,2 |
1,450 |
-7,940 |
1,450 |
7,940 |
2,103 |
63,044 |
-11,513 |
14 |
102,4 |
101,8 |
-0,850 |
-5,340 |
0,850 |
5,340 |
0,722 |
28,516 |
4,539 |
15 |
100,5 |
102,7 |
-2,750 |
-4,440 |
2,750 |
4,440 |
7,563 |
19,714 |
12,210 |
16 |
101,4 |
103,2 |
-1,850 |
-3,940 |
1,850 |
3,940 |
3,422 |
15,524 |
7,289 |
17 |
102,5 |
99,2 |
-0,750 |
-7,940 |
0,750 |
7,940 |
0,563 |
63,044 |
5,955 |
18 |
100,8 |
91,5 |
-2,450 |
-15,640 |
2,450 |
15,640 |
6,003 |
244,610 |
38,318 |
19 |
102,5 |
90,6 |
-0,750 |
-16,540 |
0,750 |
16,540 |
0,563 |
273,572 |
12,405 |
20 |
101,3 |
89,6 |
-1,950 |
-17,540 |
1,950 |
17,540 |
3,803 |
307,652 |
34,203 |
SUMA |
2065,00 |
2142,800 |
0,000 |
0,000 |
27,200 |
201,960 |
51,050 |
2592,228 |
234,360 |
Średni poziom zmiennych X i Y, rozrzut względem średniej oraz liniowa zależność jednej zmiennej od drugiej:
|
|
|
|
X |
Y |
Średnia arytmetyczna prosta z próby: |
103,250 |
107,140 |
|||
Mediana: |
103,250 |
102,950 |
|||
Średnie odchylenie bezwzględne z próby: |
1,360 |
10,098 |
|||
Średnie odchylenie kwadratowe z próby: |
2,553 |
129,611 |
|||
Wariancja z próby: |
2,687 |
136,433 |
|||
Odchylenie standardowe z próby: |
1,639 |
11,680 |
|||
Kowariancja z próby: |
12,335 |
||||
Współczynnik korelacji z próby: |
0,644 |
||||
Graficzna analiza zmiennych oraz uzyskanych wyników.
Wykres 1 : Liniowa zależność jednej zmiennej od drugiej.
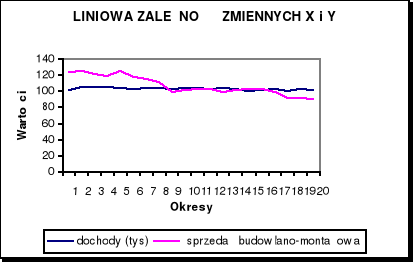
Wykres ten przedstawia jak zachowują się krzywe w stosunku do siebie w kolejnych okresach czyli od 1997 do 2001 roku .Wraz ze wzrostem jednej zmiennej czyli miesięcznego wynagrodzenia druga zmienna tez rośnie czyli zwiększa się sprzedaż budowlano- montażowa ( od 1 do 4 okresu). Od piątego okresu Czyli w pierwszym kwartale 1998 roku miesięczne wynagrodzenie spada i w związku z tym spada sprzedaż remontowo-montażowa .
Wykres 2: Odchylenie wartości X od średniej.
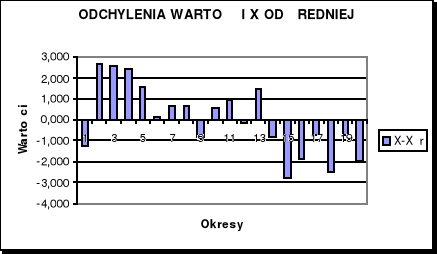
Wykres ilustruje wartość odchyleń od średniej dla X czyli przeciętne miesięczne wynagrodzenie. Można zauważyć że w okresie 1 (1kwartał 1997), 9(1 kw.1999), 12( 4 kw. 1999), i od 14 ( czyli od 2 kwartał 2000) występują odchylenia ujemne czyli miesięczne wynagrodzenie w tych okresach było niższe od średniej dla lat 1997-2001.Zaś w pozostałych okresach występują dodatnie odchylenia czyli miesięczne wynagrodzenie w tych okresach było wyższe od średniej dla tych lat. Największe ujemne odchylenie było w 15 okresie tzn. w trzecim kwartale 2000 roku, zaś najwyższa dodatnia w drugim kwartale 1997 roku.
Wykres 3: Odchylenia wartości Y od średniej.
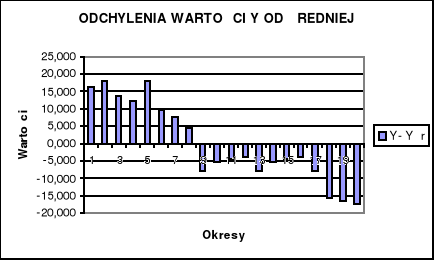
Powyższy wykres przedstawia wartość odchyleń od średniej Y czyli sprzedaż budowlano- montażowa. Począwszy od I kwartału 1997 do ostatniego 1998 roku występują odchylenia dodatnie, a największe odchylenie było w i kwartale 1998 roku. Jak widać na wykresie od 9 do 20 okresu czyli od 1999 do 2001roku występują odchylenia ujemne (największe ujemne odchylenie było w 20 ostatnim okresie 2001 roku).
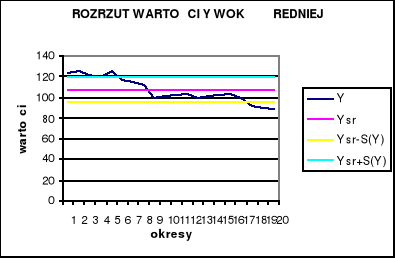
Wykres 4: Rozrzut wartości X wokół średniej.
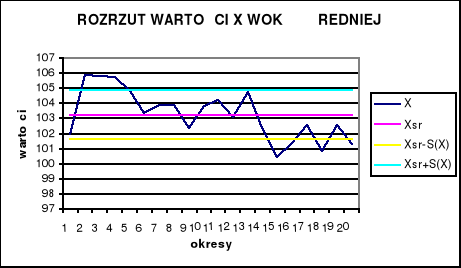
Wykres 5: Rozrzut wartości Y wokół średniej.
Wykres 6: Korelacje zmiennych X i Y.
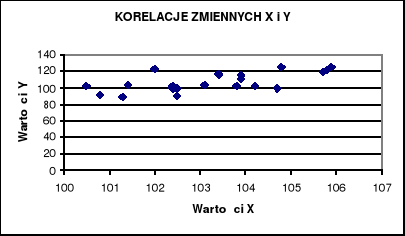
Wykres korelacji zmiennych ilustruje zgodność zmian dwóch cech. Jak widać mamy tu do czynienia z słabą korelacją dodatnia co oznacza, że sprzedaż budowlano-montażowa i miesięczne wynagrodzenie są jednak współzależne od siebie.
WNIOSKI
Po przeprowadzeniu analizy poziomu średniego zmiennych, rozrzutu względem średniej oraz liniowej zależności jednej zmiennej od drugiej można wysnuć następujące wnioski:
Dla potrzeb zadania przedstawione zostały dane z dwudziestu lat, ilustrujące w jaki sposób kształtują się sprzedaż budowlano- remontowa i miesięczne wynagrodzenie .
W okresie od stycznia 1997 roku do grudnia 2001 roku w Polsce średnie miesięczne wynagrodzenie realne brutto w gospodarce narodowej ogółem wynosiło 1032500, zaś średnia sprzedaż produkcji budowlano-montażowej 1071400. Z danych statystycznych widać ,że w badanym okresie przeciętne miesięczne wynagrodzenie na początku 1997 i w związku z tym sprzedaż budowlano- montażowa też wzrosła. Jednak w dalszych okresach od początku 1998 miesięczne wynagrodzenie zaczęło spadać co jest związane ze spadkiem sprzedaży budowlano- montażowej.
Mediana zmiennej X wynosi 103,250 co oznacza, że w połowie okresów przeciętne miesięczne wynagrodzenie wynosiło mniej niż 103,250 tys. zł . W przypadku zmiennej Y mediana wynosi 102,950 co pozwala stwierdzić ,że w połowie okresów sprzedaż budowlano- montażowa wynosiła mniej niż 102,950 tys. zł.
Odchylenie wszystkich wartości zmiennej X od przeciętnego miesięcznego wynagrodzenia wynosi średnio 1,639 tys., a wartości Y od przeciętnej sprzedaży budowlano-montażowej średnio 11,680 tys.
Kowariancja w badanym zjawisku wynosi 12,335 , wynik ten ma wartość dodatnią, co oznacza, że większe wartości X ( wyższe miesięczne wynagrodzenie) odpowiadają większym wartościom Y ( wyższej sprzedaży budowlano- montażowej ).
Współczynnik korelacji jest wykorzystywany do wyznaczania zależności pomiędzy dwoma własnościami. Jeżeli współczynnik korelacji zbliża się do 0, wówczas nie ma związku statystycznego pomiędzy badanymi cechami a zjawiskiem. Wskaźnik korelacji dla 20 okresów jest równy 0,644 co mówi o dodatniej korelacji między dwiema badanymi stanami zmiennej. Wraz ze wzrostem ( spadkiem) miesięcznego wynagrodzenia następuję wzrost (spadek ) sprzedaży budowlano-montażowej.
Zadanie 2
Przedstaw przykłady 2 prognoz przyjmując podane kryterium klasyfikacji (prognoza ze względu na cel lub funkcję). W podanych prognozach wskaż obiekt, zjawisko, zmienną.
Podaj, na podstawie Rocznika Statystycznego, przykłady:
wielowymiarowego szeregu czasowego
wielowymiarowego szeregu przekrojowego
szeregu przekrojowo-czasowego
1. Do przykładów swoich prognoz zastosowałam kryterium ze względu na cel lub funkcję.
Przykłady prognoz:
prognoza preparacyjna
Treść prognozy: W 2004 r. w Polsce stopa bezrobocia wzrośnie o 1,7%. |
||
obiekt |
zjawisko |
zmienna |
Polska |
Stopa bezrobocia |
mierzalna |
Treść prognozy: W 2006 roku sprzedaż rowerów w woj. podlaskim wzrośnie do 250000 szt. |
||
obiekt |
zjawisko |
zmienna |
Polska |
Sprzedaż rowerów |
mierzalna |
b)prognoza ostrzegawcza
Treść prognozy: W 2006 roku w Polsce spadnie cena na mikroprocesory o 2,1% ,więc wzrośnie sprzedaż sprzętu komputerowe. |
||
obiekt |
zjawisko |
zmienna |
Polska |
Spadek cen mikroprocesorów |
mierzalna |
Treść prognozy: W 2020 r. zwiększy się dziura ozonowa, w związku z czym zwiększy się popyt na kremy z filtrem przeciwko UV. |
||
obiekt |
zjawisko |
zmienna |
Świat |
Zwiększenie dziury ozonowej |
niemierzalna |
prognoza badawcza
Treść prognozy: W 2006 roku Polska przystąpi do UE w związku z czym Polacy częściej będą odwiedzać kraje europejskie. |
||
obiekt |
zjawisko |
zmienna |
Polska |
Przystąpienie Polski do UE |
niemierzalna |
Treść prognozy: W 2005 w związku z uprzemysłowieniem miast nastąpi w Polsce wzrost emigracji ludności z miast na wieś |
||
obiekt |
zjawisko |
zmienna |
Polska |
Wzrost emigracji |
mierzalna |
d) prognoza normatywna
Treść prognozy: Za 3 lata w celu zmniejszenia zachorowalności na raka płuc w co drugiej polskiej szkole średniej będą prowadzone zajęcia dotyczące walki z nałogiem nikotynowym. |
||
obiekt |
zjawisko |
zmienna |
Polskie szkoły średnie |
Zmniejszenie zachorowalności na raka płuc |
mierzalna |
Treść prognozy: W 2010r. w celu zwiększenia zainteresowania Polaków kulturą, zwiększy się ilość emitowanych programów kulturalno-rozrywkowych. |
||
Obiekt |
zjawisko |
zmienna |
Polska |
Zwiększenie zainteresowania kulturą |
niemierzalna |
e) prognoza pasywna
Treść prognozy: W 2004 r. w województwie podlaskim zwiększy się ilość zwierząt chorych na wściekliznę |
||
obiekt |
zjawisko |
zmienna |
Woj. podlaskie |
wzrost ilości zwierząt chorych na wściekliznę |
mierzalna |
Treść prognozy: W listopadzie 2003 r. na obszarze północno-wschodniej Polski spadnie pierwszy śnieg |
||
obiekt |
zjawisko |
zmienna |
Północno-wschodnia Polska |
Opad pierwszego śniegu |
niemierzalna |
f) prognoza aktywna
Treść prognozy: W XII br. wzrośnie liczba osób korzystających z komunikacji miejskiej w Białymstoku, więc trzeba będzie zakupić dodatkowe autobusy. |
||
obiekt |
zjawisko |
zmienna |
Białystok |
Wzrost liczby osób |
mierzalna |
Treść prognozy: W 2007 roku w Polsce zmniejszy się przyrost naturalny i w związku z czym trzeba będzie zlikwidować szkoły w mniejszych miejscowościach. |
||
obiekt |
zjawisko |
zmienna |
Polska |
Spadek przyrostu naturalnego |
mierzalna |
2 Przykłady szeregów :
wielowymiarowego szeregu czasowego:
wielowymiarowego szeregu przekrojowego:
szeregu przekrojowo-czasowego
metoda naiwna,
metoda średniej ruchomej,
metoda wygładzania wykładniczego prostego.
Cel prognozy, wybór postawy, podanie przesłanek prognostycznych.
Analiza graficzna zmiennej prognozowanej (określenie typu szeregu, omówienie wyników dekompozycji szeregu).
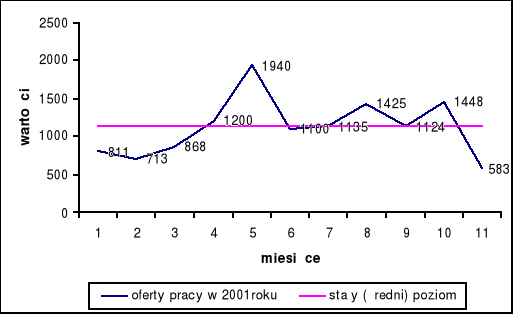
stały (średni) poziom zmiennej wynoszący 1123,82 - mówi o tym, że w Polsce w miesiącach styczeń- listopada 2001 roku przeciętnie w ciągu miesiąca tyle było zgłaszanych ofert pracy.
wahania sezonowe na rynku pracy, co np. jest spowodowane, że w okresie letnim (prace sezonowe itp.) jest wzrost ofert pracy, zaś okres jesienno-zimowym jest „okresem martwym” i maleje ilość zgłaszanych ofert pracy.
metoda naiwna- oparta na prostych przesłankach dotyczących przyszłości i umożliwia konstrukcję prognozy na 1 okres naprzód.
Lata |
Uczniowie szkół podstawowych (tys.) |
Uczniowie szkół ogólnokształcących (tys.) |
Uczniowie szkół ogólnokształcących (tys.) |
Uczniowie szkół zawodowych (tys.) |
1990 |
5287,0 |
445,0 |
1451,1 |
814,5 |
1991 |
5310,5 |
499,8 |
1477,9 |
806,2 |
1992 |
5312,6 |
555,8 |
1502,0 |
792,8 |
1993 |
5278,4 |
602,4 |
1534,1 |
769,5 |
Źródło: Rocznik statystyczny Polska w latach 1946-1994 ( załączone w pracy )
Województwa |
żyto |
kukurydza |
Buraki cukrowe |
podlaskie |
303,9 |
256,1 |
233,3 |
lubelskie |
391,9 |
249,7 |
2154,7 |
warmińsko- mazurskie |
219,6 |
225,9 |
255,5 |
mazowieckie |
980,7 |
335,3 |
935,4 |
małopolskie |
58,4 |
197,6 |
85,1 |
Źródło: www.stat.gov.pl Tab.17 . Zbiory głównych ziemiopłodów w 1999 r. ( załączone w pracy )
Województwa |
Zmienna |
Lata |
|||
|
Nazwa |
Symbol |
1996 |
1999 |
2000 |
lubelskie |
pszenica |
P |
3,0 |
1017,2 |
967,7 |
|
ziemniaki |
Z |
21,0 |
222,1 |
2495,5 |
mazowieckie |
pszenica |
P |
3,0 |
511,6 |
445,6 |
|
ziemniaki |
Z |
20,4 |
3228,6 |
4240,8 |
podlaskie |
pszenica |
P |
2,8 |
194,0 |
132,4 |
|
ziemniaki |
Z |
20,4 |
1405,2 |
1479,1 |
Zródło:www.stat.gov.pl Tab.17, 18 i 20 Zbiory głównych ziemiopłodów w 1996, 1999 i 2000 roku.( załączone w pracy )
Zadanie 3
Na podstawie dobranych i udokumentowanych danych nt. analizowanego zjawiska gospodarczego z okresu poprzedniego zbuduj prognozę badanej wielkości na jeden krok naprzód. Do budowy prognozy należy wykorzystać proste metody prognozowania na podstawie szeregów czasowych:
Zebrane przeze mnie dane pochodzą ze strony internetowej Głównego Urzędu Statystycznego: www.stat.gov.pl . Dotyczą one ofert pracy zgłaszanych w Polsce w miesiącach styczeń-listopad 2001 roku ( w tys. sztuk ). Celem przeprowadzanej prognozy jest zorientowanie w jaki sposób będą się kształtowały oferty pracy w Polsce Naszą prognozę badanej wielkości wyznaczymy na jeden krok naprzód , czyli w tym przypadku na miesiąc grudzień. Co pozwala nam zauważyć się jak wygląda sytuacja na polskim rynku pracy .
Dane przedstawia poniższa tabela:
2001 rok |
Oferty pracy w Polsce w roku 2001 (zgłaszane w ciągu miesiąca) |
Styczeń |
811 |
Luty |
713 |
Marzec |
868 |
Kwiecień |
1200 |
Maj |
1940 |
Czerwiec |
1115 |
Lipiec |
1135 |
Sierpień |
1425 |
Wrzesień |
1124 |
Październik |
1448 |
Listopad |
583 |
Typ szeregu: szereg ze stałym (średnim) poziomem prognozowanej zmiennej oraz z wahaniami sezonowymi.
Dekompozycja szeregu:
3. Wyniki obliczeń dla 3 metod:
Miesiące |
Yt |
Y*t prognoza |
qt |
względny błąd |
Mod. wzg błędu |
qt2 |
Licznik U-Theila |
Mianownik U-Theila |
styczeń |
811 |
|
|
|
|
|
0,014601936 |
0,014601936 |
luty |
713 |
811 |
-98 |
-13,74% |
0,137 |
9604 |
0,047258979 |
0,047258979 |
marzec |
868 |
713 |
155 |
17,86% |
0,179 |
24025 |
0,146297437 |
0,146297437 |
kwiecień |
1200 |
868 |
332 |
27,67% |
0,277 |
110224 |
0,380277778 |
0,380277778 |
maj |
1940 |
1200 |
740 |
38,14% |
0,381 |
547600 |
0,180844139 |
0,180844139 |
czerwiec |
1115 |
1940 |
-825 |
-73,99% |
0,740 |
680625 |
0,000321744 |
0,000321744 |
lipiec |
1135 |
1115 |
20 |
1,76% |
0,018 |
400 |
0,065283627 |
0,065283627 |
sierpień |
1425 |
1135 |
290 |
20,35% |
0,204 |
84100 |
0,044617298 |
0,044617298 |
wrzesień |
1124 |
1425 |
-301 |
-26,78% |
0,268 |
90601 |
0,083091653 |
0,083091653 |
październik |
1448 |
1124 |
324 |
22,38% |
0,224 |
104976 |
0,356857716 |
0,356857716 |
listopad |
583 |
1448 |
-865 |
-148,37% |
1,484 |
748225 |
|
|
grudzień |
|
583 |
|
|
|
|
|
|
Suma |
|
|
|
|
|
1,319452305 |
1,319452305 |
|
Moduł śr. błędu |
39,10% |
(S*)2 |
240038 |
S* |
489,937 |
U-Theila |
1 |
Odchylenie standardowe błędu-S |
515,879 |
Wykres prognozy metodą naiwną :
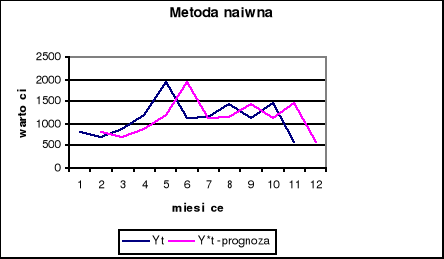
Wartość modułu względnego błędu prognozy wynosi 39,10 %, co oznacza, że wartości przeciętnie różnią się od wartości rzeczywistych o 39,10 % liczone w procentach wartości rzeczywistej. Średni błąd kwadratowy prognozy ( S*2 ) wynosi 240038, a jego pierwiastek( S* ) 489,937, co oznacza że wyznaczając prognozę tą metodą przeciętnie myliliśmy się o te właśnie wartość.
Odchylenie standardowe błędu prognozy (S) jest równa 515,879.Jest więc spełniony warunek S*<=S .
Wartość statystyki U-Theila wynosi 1 ,co potwierdza trafność obliczeń
b) metoda średniej ruchomej -polega na uśrednianiu informacji z przeszłości pozwala na bardziej dokładną konstrukcję prognozy , w tym celu przyjmuję się liczbę wyrazów średniej ruchomej k czyli stałą wygładzania ja wybrałam k=3 , k=5, k=7 .
Dla k= 3
Miesiące |
Yt |
Y*t |
qt |
względny błąd |
mod wzg błędu |
qt2 |
Licznik U-Theila |
Mianownik U-Theila |
styczeń |
811 |
|
|
|
|
|
|
|
luty |
713 |
|
|
|
|
|
|
|
marzec |
868 |
|
|
|
|
|
0,215204778 |
0,146297437 |
kwiecień |
1200 |
797,3 |
402,667 |
33,56% |
0,336 |
162140,44 |
0,712617361 |
0,380277778 |
maj |
1940 |
927,0 |
1013,000 |
52,22% |
0,522 |
1026169,00 |
0,012977203 |
0,180844139 |
czerwiec |
1115 |
1336,0 |
-221,000 |
-19,82% |
0,198 |
48841,00 |
0,064572204 |
0,000321744 |
lipiec |
1135 |
1418,3 |
-283,333 |
-24,96% |
0,250 |
80277,78 |
0,000623166 |
0,065283627 |
sierpień |
1425 |
1396,7 |
28,333 |
1,99% |
0,020 |
802,78 |
0,005023576 |
0,044617298 |
wrzesień |
1124 |
1225,0 |
-101,000 |
-8,99% |
0,090 |
10201,00 |
0,038310052 |
0,083091653 |
październik |
1448 |
1228,0 |
220,000 |
15,19% |
0,152 |
48400,00 |
0,267801485 |
0,356857716 |
listopad |
583 |
1332,3 |
-749,333 |
-128,53% |
1,285 |
561500,44 |
|
|
grudzień |
|
1051,7 |
|
|
|
|
|
|
Suma |
|
|
|
|
|
1,317129824 |
1,25759139 |
|
Moduł śr. błędu |
35,66% |
(S*)2 |
242291,556 |
S* |
492,23 |
U-Theila |
1,02 |
Odchylenie standardowe błędu-S |
524,591 |
Dla k= 5
Miesiące |
Yt |
Y*t |
qt |
względny błąd |
mod wzg błądu |
qt2 |
Licznik U-Theila |
Mianownik U-Theila |
styczeń |
811 |
|
|
|
|
|
|
|
luty |
713 |
|
|
|
|
|
|
|
marzec |
868 |
|
|
|
|
|
|
|
kwiecień |
1200 |
|
|
|
|
|
|
|
maj |
1940 |
|
|
|
|
|
1,96514E-05 |
0,180844139 |
czerwiec |
1115 |
1106,4 |
8,600 |
0,77% |
0,008 |
73,96 |
0,000833992 |
0,000321744 |
lipiec |
1135 |
1167,2 |
-32,200 |
-2,84% |
0,028 |
1036,84 |
0,023340302 |
0,065283627 |
sierpień |
1425 |
1251,6 |
173,400 |
12,17% |
0,122 |
30067,56 |
0,028129763 |
0,044617298 |
wrzesień |
1124 |
1363,0 |
-239,000 |
-21,26% |
0,213 |
57121,00 |
0,007946993 |
0,083091653 |
październik |
1448 |
1347,8 |
100,200 |
6,92% |
0,069 |
10040,04 |
0,211803364 |
0,356857716 |
listopad |
583 |
1249,4 |
-666,400 |
-114,31% |
1,143 |
444088,96 |
|
|
grudzień |
|
1143,0 |
|
|
|
|
|
|
Suma |
|
|
|
|
|
0,272074065 |
0,731016175 |
|
Moduł śr. błędu |
26,38% |
(S*)2 |
90404,727 |
S* |
300,67 |
U-Theila |
0,61 |
Odchylenie standardowe błędu-S |
306,867 |
Dla k= 7
Miesiące |
Yt |
Y*t |
qt |
względny błąd |
mod wzg bl |
qt2 |
Licznik U-Theila |
Mianownik U-Theila |
styczeń |
811 |
|
|
|
|
|
|
|
luty |
713 |
|
|
|
|
|
|
|
marzec |
868 |
|
|
|
|
|
|
|
kwiecień |
1200 |
|
|
|
|
|
|
|
maj |
1940 |
|
|
|
|
|
|
|
czerwiec |
1115 |
|
|
|
|
|
|
|
lipiec |
1135 |
|
|
|
|
|
0,076188506 |
0,065283627 |
sierpień |
1425 |
1111,7 |
313,286 |
21,98% |
0,220 |
98147,94 |
0,002801832 |
0,044617298 |
wrzesień |
1124 |
1199,4 |
-75,429 |
-6,71% |
0,067 |
5689,47 |
0,02853128 |
0,083091653 |
październik |
1448 |
1258,1 |
189,857 |
13,11% |
0,131 |
36045,73 |
0,274032005 |
0,356857716 |
listopad |
583 |
1341,0 |
-758,000 |
-130,02% |
1,300 |
574564,00 |
|
|
grudzień |
|
1252,9 |
|
|
|
|
|
|
Suma |
|
|
|
|
|
0,381553623 |
0,549850293 |
|
Moduł śr. błędu |
42,96% |
(S*)2 |
178611,786 |
S* |
422,62 |
U-Theila |
0,83 |
Odchylenie standardowe błędu-S |
478,600 |
Wykres dla metody średniej ruchomej dla k=3 k=5 k=7:
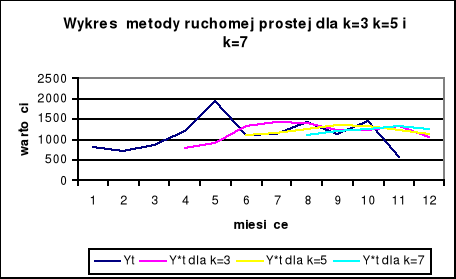
Wykres prognozy dla k=3 odzwierciedla charakter wykresu danych rzeczywistych, jednak wartości odbiegają od rzeczywistości. Dla k=5 wykres prognozy ani nie oddaje dokładnie ani charakteru danych rzeczywistych ani też ich wartości i widać duże spłaszczenie wykresu, co świadczy o wygładzaniu tego szeregu. Zaś przy k= 7 wykres jest spłaszczony, co świadczy o znacznym wygładzeniu szeregu. Wartości również odbiegają od wartości rzeczywistych, jednak różnica ta jest mniejsza niż przy poprzednich k .
|
|
|
|
k=3 |
k=5 |
k=7 |
Moduł śr. błędu |
35,66% |
26,38% |
42,96% |
|||
(S*)2 |
242291,556 |
90404,727 |
178611,786 |
|||
S* |
492,23 |
300,67 |
422,62 |
|||
U-Theila |
1,02 |
0,61 |
0,83 |
|||
Odchylenie standardowe błędu- S |
524,591 |
306,867 |
478,600 |
|||
Średnia wartość moduły względnego błędu prognozy jest równa dla k= 3 , k=5 i k=7 odpowiednio 35,66 %, 26,38% i 42,96% ,czyli wartości prognozy przeciętnie różnią się od wartości rzeczywistych o tą wartość. Najmniejszy błąd wyszedł dla k=5 .
Średni błąd kwadratowy wyniósł odpowiednio S*2 [ 242291,556; 90404,727; 178611,786] a jego pierwiastek czyli S* [492,23; 300,67; 422,62 ]. Oznacza to ,że przy k=3 przeciętne odchylenie prognozy od wartości rzeczywistych wynosi 492,23. Wartość S* jest najniższa przy k=5 , co świadczy że z metod średniej ruchomej najbardziej trafna jest metoda dla k=5. We wszystkich prognozach wyznaczonych metodą średniej ruchomej spełniony jest warunek S* <= S.
Statystyka U-Theila w przypadku k=5 jest najmniejsza (0,61) w porównaniu z pozostałymi dwiema, czyli metoda ta da lepsze wyniki niż pozostałe.
C ) metoda wygładzania wykładniczego - metoda ta polega na tym, że szereg czasowy wygładza się za pomocą ważonej średniej ruchomej.
Miesiące |
Yt |
Y*t |
qt |
względny błąd |
mod wzg błędu |
qt2 |
Licznik U-Theila |
Mianownik U-Theila |
styczeń |
811 |
|
|
|
|
|
0,014602 |
0,014602 |
luty |
713 |
811 |
-98 |
-13,74% |
0,137 |
9604 |
0,015052 |
0,047259 |
marzec |
868 |
780,5254 |
87,47457 |
10,08% |
0,101 |
7651,801 |
0,204238 |
0,146297 |
kwiecień |
1200 |
807,727 |
392,273 |
32,69% |
0,327 |
153878,1 |
0,708809 |
0,380278 |
maj |
1940 |
929,7102 |
1010,29 |
52,08% |
0,521 |
1020686 |
0,004413 |
0,180844 |
czerwiec |
1115 |
1243,875 |
-128,875 |
-11,56% |
0,116 |
16608,76 |
0,003807 |
0,000322 |
lipiec |
1135 |
1203,799 |
-68,7994 |
-6,06% |
0,061 |
4733,351 |
0,045685 |
0,065284 |
sierpień |
1425 |
1182,405 |
242,5948 |
17,02% |
0,170 |
58852,26 |
0,008822 |
0,044617 |
wrzesień |
1124 |
1257,844 |
-133,844 |
-11,91% |
0,119 |
17914,13 |
0,042521 |
0,083092 |
październik |
1448 |
1216,223 |
231,777 |
16,01% |
0,160 |
53720,59 |
0,237251 |
0,356858 |
listopad |
583 |
1288,298 |
-705,298 |
-120,98% |
1,210 |
497444,6 |
|
|
grudzień |
|
1068,975 |
|
|
|
|
|
|
Suma |
|
|
|
|
|
1,285201 |
1,319452 |
|
Alfa =0,311
Moduł śr. błędu |
29,21% |
(S*)2 |
1814109,318 |
S* |
429,08 |
U-Theila |
0,987 |
Odchylenie standardowe błędu-S |
443,756 |
Wykres dla metody wygładzania wykładniczego:
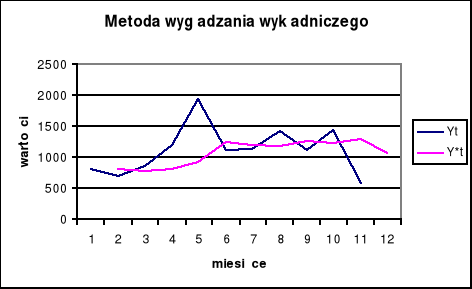
Wykres prognozy odbiega od wykresu danych rzeczywistych zarówno pod względem charakteru, jak i wartości. Wykres jest spłaszczony, co świadczy o wygładzaniu szeregu , wynika to z faktu, że alfa ma wartość małą i wynosi 0,311.Ustalene wartości alfa na tym poziomie pozwoliło zastosowanie narzędzia solver. Parametr wygładzania alfa jest liczbą z przedziału < 0;1 >Alfa minimalizuje wartość S* .Moduł błędu prognozy wynosi 29,21% czyli o tyle procent wartości prognozy przeciętnie różnią się od wartości rzeczywistych .Jest to wartość nie zbyt duża, tak więc trafność prognozy jest dość dobra. Średni błąd kwadratowy wynosi 1814109,318 , a jego pierwiastek ( S*) 429,08. Oznacza to, że przeciętne odchylenie prognozy od wartości rzeczywistych wynosi w tym przypadku 429,08. Również spełniony jest warunek S*<S gdyż S wynosi 443,756.
Statystyka U -Theila wynosi 0,987.
Wnioski : Ocena trafności prognozy
Z powyższej analizy wynika, iż różne metody dały różne wyniki. Prognoza na miesiąc grudzień 2001 dla poszczególnych metod wynosi :
metoda naiwna : 583
metoda średniej ruchomej dla k = 3 : 1051,7
dla k = 5 : 1143,0
dla k= 7 : 1252,9
metoda wygładzania wykładniczego : 1068,975
|
|
|
|
Metoda naiwna |
Metoda śr. ruchomej |
Metoda wygładzania wykładniczego |
|||
|
|
|
|
|
k=3 |
k=5 |
k=7 |
|
|
Moduł śr. błędu |
39,10% |
35,66% |
26,38 |
42,96% |
29,21% |
|
|||
(S*)2 |
240038 |
242291,6 |
90404,73 |
178611,8 |
1814109,318 |
|
|||
S* |
489,937 |
492,23 |
300,67 |
422,62 |
429,08 |
|
|||
U-Theila |
1 |
1,02 |
0,61 |
0,83 |
0,987 |
|
|||
Odchylenie standardowe błędu |
515,879 |
524,591 |
306,867 |
478,600 |
443,756 |
|
|||
Z przeprowadzonej analizy wynika, iż najlepszą metodą prognozowania dla przedstawionych danych jest metoda średniej ruchomej przy stałej wygładzania k równej 5. Prognoza wyznaczona z wykorzystaniem tej metody jest obarczona najmniejszym spośród wszystkich przedstawionych metod błędem względnym prognozy 26,38 % oraz średnim błędem kwadratowym 90404,73 . Wartość S* jest w związku z tym również najmniejsza (300,67). Statystyka U-Theila w poszczególnych metodach jest również najmniejsza i wynosi 0,61. W związku z powyższym ta metoda jest najbardziej trafna .
9
Wyszukiwarka
Podobne podstrony:
prognozowanie, statystyka
prognozy, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Statystyka SUM w4
statystyka 3
Weryfikacja hipotez statystycznych
Zaj III Karta statystyczna NOT st
Metodologia SPSS Zastosowanie komputerów Brzezicka Rotkiewicz Podstawy statystyki
metody statystyczne w chemii 8
Metodologia SPSS Zastosowanie komputerów Golański Statystyki
PROGNOZY GOSPODARCZE DLA POLSKI
prognozowanie 1
Statystyka #9 Regresja i korelacja
06 Testowanie hipotez statystycznychid 6412 ppt
BHP STATYSTYKA
więcej podobnych podstron