9EKRAN_223
Lekcja 9- Prawo Faradaya
Lekcja 9 jest kontynuacją zagadnień związanych z prawami i własnościami pola magnetycznego. W lekcji tej czytelnik pozna jedno z ważniejszych praw magnetyzmu - prawo Faradaya. Z prawem tym związana jest tzw. reguła Lenza pozwalająca na określanie zwrotów wyznaczanych wielkości. Zdefiniowano następny element obwodu jakim jest cewka oraz jej charakterystyczną wielkość- indukcyjność własną.
9EKRAN_224
Indukcja elektromagnetyczna.
Zjawisko indukcji elektromagnetycznej polega na indukowaniu siły elektromotorycznej przy zmianach strumienia magnetycznego.
Prawo Faradaya
![]()
![]()
-strumień sprzężony
Komentarz-EKRAN_224
Podana tu definicja strumienia sprzężonego jest prawdziwa jeżeli strumień wytwarzany przez każdy zwój przenika wszystkie pozostałe ( nie ulega rozproszeniu).
9EKRAN_225
Reguła Lenza
Każda zmiana strumienia powoduje wyindukowanie siły elektromotorycznej o takim kierunku by prąd płynący pod jej wpływem wywołał strumień przeciwdziałający pierwotnej zmianie strumienia.
a)
Komentarz-EKRAN_225
W zależności od sposobu zastrzałkowania można przyjąć we wzorze Faradaya znak plus lub minus. W przypadku a) jeżeli magnes porusza się w lewo czyli strumień narasta to pochodna ma znak dodatni i siła elektromotoryczna generuje strumień o przeciwnym zwrocie (przeciwdziałanie zgodnie z regułą Lenza). Z kolei jeżeli magnes zacznie poruszać się w prawo strumień zacznie maleć (pochodna ujemna) co oznacza, że zmieni się zwrot SEM a stąd zwrot d ) przeciwdziałanie zostanie zachowane).
9EKRAN_226
b)
Komentarz-EKRAN_226
Ponieważ w każdym z przypadków a i b przy poruszaniu się magnesu zgodnie z zastrzałkowaną prędkością v strumień narastał (czyli jego pochodna była dodatnia) stąd strumień d przeciwdziałający musi mieć rzeczywisty zwrot przeciwny do , a taki wywoła zwrot prądu wymuszony zwrotem SEM jak na rys. a. Zastrzałkowanie prawoskrętne (rys.b) musi oznaczać że wartości e,i,d<0
W dalszym ciągu będziemy przyjmowali lewoskrętne strzałkowanie SEM względem strumienia wzbudzającego tą SEM.
9EKRAN_227
Rozważmy z kolei dwie cewki nawinięte różnie na rdzeń, oraz rozpatrzmy zjawisko zachodzące w czasie I ćwiartki prądu sinusoidalnego. (przebieg sinusoidalny prądu poniżej)
a) prawoskrętnie nawinięta cewka
b) lewoskrętnie nawinięta
Komentarz-EKRAN_227
Z rysunków a) i b) wynika, że bez względu na sposób nawinięcia cewek można przyjąć (przy lewostronnym strzałkowaniu SEM względem strumienia d) odbiornikowy sposób strzałkowania prądu i napięcia.
Łatwo wykazać, że wzór ![]()
jest poprawny dla odbiornikowego strzałkowania cewki dla pozostałych ćwiartek.
9EKRAN_228
Rodzaje indukowanych sił elektromotorycznych
Załóżmy, że pionowo ustawiona ramka (liczba zwojów z=1) nie porusza się (poruszają się magnesy).
Wówczas: ![]()
gdzie: Sr - pole powierzchni ramki
B(t) - pole magnetyczne magnesu prostopadłe do ramki
![]()
- sem indukcji własnej-zwane sem transformacji
Komentarz-EKRAN_228
Zakładamy że każdym punkcie powierzchni ramki pole jest jednakowe i wówczas strumień można wyznaczyć na podstawie iloczynu (bez konieczności całkowania) Z drugiej strony ruch magnesów zmienia wartość pola magnetycznego w czasie.
9EKRAN_229
Tym razem założymy, że magnesy są nieruchome, a obraca się ramka.
Wówczas: ![]()
![]()
gdzie: S(t)=Sr cos(t)
![]()
- sem rotacji
Komentarz-EKRAN_229
Tym razem zakładamy, że pole w każdym punkcie przestrzeni jest stałe, a zmiana strumienia następuje w wyniku ruchu obrotowego ramki.
9EKRAN_230
Jeżeli jednocześnie obraca się ramka i magnesy się przemieszczają.
Wówczas: ![]()
gdzie: ![]()
![]()
et-sem rotacji - występuje ruch względny przewodnika i pola magnetycznego z równoczesnym przecinaniem lini pola.
er-sem transformacji - gdy występuje zmiana w czasie strumienia magnetycznego
przenikającego nieruchomą pętlę przewodnika.
Komentarz-EKRAN_230
Siła elektromotoryczna transormacji jest związana z urządzeniem zwanym transformatorem, z kolei SEM rotacji zawsze wystepuje w maszynach wirujących.
9EKRAN_231
Pytanie
Wyobraźmy sobie, że na rdzeń cewki nałożono dodatkowy zwój a przez uzwojenie cewki płynie prąd stały. Czy jeżeli dodatkowy zwój zacznie oddalać się od cewki ruchem prostoliniowym zaindukuje się w nim siła elektromotoryczna, jeżeli tak jakiego rodzaju?
Odpowiedź-EKRAN_231
Pomimo, że oddalający się zwój nie rotuje ( nie obraca się) to zaindukuje się w nim właśnie siła elektromotoryczna rotacji gdyż jest ona wynikiem jego ruchu. Zauważ, że gdyby zwój nie poruszał się (zatrzymał w pewnej odległości od cewki) to nic się w nim nie zaindukuje (brak zmiany strumienia - pochodna = zero). Indukowanie się SEM w poruszającym się zwoju pomimo przepływu prądu stałego jest spowodowane tym, że pole generowane przez cewkę nie jest jednorodne.
Odpowiedź: SEM rotacji
9EKRAN_232
Indukcyjność własna cewki ![]()
Komentarz-EKRAN_232
Indukcyjnością własną cewki nazywamy wielkość określaną jako stosunek strumienia sprzężonego z cewką a wytworzonego przez prąd i płynący przez jej uzwojenie.
Jeszcze raz należy podkreślić, że strumień sprzężony jest równy iloczynowi liczby zwojów razy strumień wypadkowy w sytuacji gdy pominiemy wszelkie rozproszenia strumieni wytwarzanych przez poszczególne zwoje.
Należy pamiętać, że podobnie jak w przypadku rezystancji indukcyjność własna może mieć charakter liniowy bądź nieliniowy. W pierwszym przypadku będzie można określić L=const. W drugim indukcyjność własna będzie zależała od punktu pracy.
9EKRAN_233
Oblicz jednostkową indukcyjność własną dla dwuprzewodowej linii (pominąć indukcyjność wewnętrzną) .
Dane: promień przewodów R=0,25 cm, odległość pomiędzy przewodami a=0,4 m.
Komentarz-EKRAN_233
W linii dwutorowej prąd płynie jednym przewodem i powraca drugim. Zatem układ linii można wyobrazić sobie jak olbrzymi wydłużony zwój (cewkę jednozwojową), dla której będziemy określać indukcyjność własną. Jeżeli odległość pomiędzy przewodami jest znacznie większa od ich promieni to możemy pominąć zjawiska zachodzące wewnątrz przewodów (indukcyjność wewnętrzna).
9EKRAN_234
Rozwiązanie
Natężenie pola magnetycznego pochodzące od pierwszego przewodu w odległości r od przewodu (rysunek)
![]()
Wychodząc z wzoru ![]()
elementarny strumień magnetyczny przechodzący przez pasek o powierzchni ldr ma postać:
![]()
Oznacza to założenie stałości pola w elementarnym pasku o szerokości dr.
Komentarz-EKRAN_234
Zagadnienie określenia zewnętrznej indukcyjności własnej sprowadzimy do wyznaczenia strumienia wytwarzanego przez prądy obu przewodów. W tym celu wykorzystujemy wzór na natężenie pola magnetycznego wokół nieskończenie długiego przewodu wyznaczonego w lekcji 8 (ekran nr 197).
9EKRAN_235
Całkowity strumień magnetyczny przechodzący przez powierzchnię między osiami przewodów, pochodzący od pierwszego przewodu (pomija się strumień wewnątrz pierwszego przewodu) ma postać:
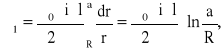
Strumień magnetyczny Φ2 pochodzący od drugiego przewodu jest taki sam.
Φ2 = Φ1
więc ![]()
stąd: ![]()
![]()
Odpowiedź: Indukcyjność własna zewnętrzna na jednostkę długości wynosi: ![]()
![]()
Komentarz-EKRAN_235
Ponieważ założenie o stałości pola może dotyczyć elementarnego paska o szerokości dr stąd całkowity strumień jest sumą strumieni elementarnych. Sumę tą określamy poprzez operacje całkowania po zmiennej r. Zakładając, że strumień wytwarzany przez drugi przewód jest identyczny, całkowity strumień jest dwukrotnie większy od wyznaczonego.
9EKRAN_236
Obliczyć indukcyjność własną cewki nawiniętej na pierścieniowym rdzeniu ferromagnetycznym o przekroju prostokątnym metodą dokładną i metodą przybliżoną (zakładając stałość indukcji B na przekroju poprzecznym rdzenia). Dane: z = 100, R1= 4cm , R2 = 6cm , a = 2cm , μr = 1000.
![]()
a) b)
Komentarz-EKRAN_236
Dla obwodów magnetycznych , dla których μr = const. zależność między strumieniem magnetycznym, a prądem jest liniowa i wówczas indukcyjność własną wyznaczymy ze wzoru
![]()
![]()
![]()
9EKRAN_237
Obliczenia metodą dokładną:
Jeżeli uzwojenie jest nawinięte równomiernie , to natężenie pola magnetycznego w rdzeniu w odległości r od osi wyrażone jest wzorem (lekcja 8 ekran 208):
![]()
, R1< r < R2
a indukcja magnetyczna w rdzeniu
![]()
, R1< r < R2
Strumień magnetyczny przenikający przez elementarną powierzchnię rdzenia o wymiarach axdr dany jest wzorem:
![]()
Komentarz-EKRAN_237
Podobnie jak w pierwszym przykładzie (linia dwutorowa) zakładamy stałość i prostopadłość pola magnetycznego w elementarnym fragmencie przekroju toroidu.
9EKRAN_238
Strumień magnetyczny w całym rdzeniu
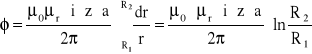
Ponieważ strumień skojarzony cewki dany jest wzorem ψ = z![]()
to po wstawieniu powyższej zależności:
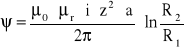
Wiedząc że indukcyjność cewki ![]()
po podstawieniu otrzymujemy:
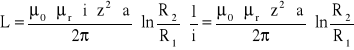
Komentarz-EKRAN_238
Po podstawieniu do wyznaczonego wzoru na indukcyjność cewki indukcyjność cewki w kształcie toroidu otrzymujemy:
![]()
9EKRAN_239
Metoda przybliżona:
Zastępując obwód magnetycznym poniższym schematem możemy na jego podstawie określić strumień: 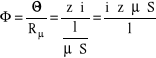
Ponieważ indukcyjność własna z definicji jest równa ![]()
stąd podstawiając określony powyżej strumień otrzymamy następujący wzór: ![]()
Komentarz-EKRAN_239
Oszacowany w ten sposób strumień bazuje na wartości średniej indukcji, stąd drogę l we wzorze na indukcyjność wyznaczymy jako średnią drogę geometryczną w rozpatrywanym toroidzie.
9EKRAN_240
Średnia długość promienia ![]()
Pole powierzchni przekroju rdzenia - ![]()
Średnia długość drogi rdzenia- ![]()
Podstawiając określoną drogę średnią oraz przekrój do oszacowanego wzoru na indukcyjność cewki otrzymany:
![]()
Odpowiedź: Indukcyjności własne cewek określone na podstawie metody dokładnej i przybliżone wynoszą odpowiednio 16.22mH i 16mH.
Komentarz-EKRAN_240
Natężenie pola magnetycznego w tej metodzie dane jest wzorem: ![]()
i jest to natężenie średnie. Stąd indukcja magnetyczna ![]()
Jak wynika z tego przykładu różnica wyliczonych indukcyjności jest nieznaczna, stąd druga metoda jest chętnie stosowana do oszacowania indukcyjności własnej cewki. Należy jeszcze raz podkreślić, że w obu przypadkach założono znajomość przenikalności magnetycznej materiału W praktyce w rzeczywistych cewkach z rdzeniem np. ferromagnetycznym jest nieznane i zależy od punktu pracy.
9EKRAN_241
Przykład
Wyznaczyć przebieg napięcia napięcia na zaciskach ab (rys. 1a), jeżeli przebiegi strumieni magnetycznych przenikających cewki podane są na rys. 1b. Dane: z1=z2=1
Komentarz-EKRAN_241
Zwróć uwagę na zastrzałkowanie strumieni względem SEM w zwojach.
9EKRAN_242
Rozwiązanie
Ponieważ siły elektromotoryczne indukowane w cewkach są zastrzałkowane prawoskrętnie względem strumieni stąd we wzorach na zależność SEM od strumienia (prawo Faradaya) przyjmujemy znak minus.
![]()
, ![]()
oraz
uab = e1 + e2
Przebiegi siły elektromotorycznej e1 w poszczególnych przedziałach czasu wyznaczymy określając funkcje strumienia w tych przedziałach:
Dla przedziału 0÷3 ms
![]()
, ![]()
, ![]()
;
Dla przedziału 3÷4 ms
![]()
, ![]()
, e1 = a2 = 3V;
Dla przedziału 4÷5 ms
![]()
, e1 = 0 ;
Dla przedziału 5÷6 ms:
![]()
, e1 = a2 = 3V
Komentarz-EKRAN_242
Analogicznie można wyznaczyć przebiegi ![]()
2 i e2 wyznacza się podobnie :
0÷1 ms: e2 = 3 V;
1÷2 ms: e2 = 0;
2÷3 ms: e2 = 3 V;
3÷5 ms: e2 = - 3 V;
9EKRAN_243
Przebiegi sił elektromotorycznych i ich suma (napięcie Uab).
Komentarz-EKRAN_243
Przebiegi e1 i e2 narysowane na rysunku 2a ( e1 - linią ciągłą, e2 - linią przerywaną). Na rysunku 2b narysowano przebieg napięcia uab.
9EKRAN_244
Zadanie
Pod wpływem siły zewnętrznej w jednorodnym polu magnetycznym o indukcji B porusza się prosty przewód o długość l ze stałą prędkością v jak na rysunku poniżej. Szyny po których porusza się przewód mają niewielką rezystancję R. Pomijając tarcie obliczyć prąd oraz moc w obwodzie.
Dane: B=1.2 T, v=2m/s, l=1m, R=0.1Ω
Komentarz-EKRAN_244
Przewód przesuwa się ze stałą prędkością w płaszczyźnie prostopadłej do linii. Oznacza to powstanie siły elektromotorycznej w obwodzie o takiej wartości, że prąd płynący pod jej wpływem determinuje elektrodynamiczną siłę działającą na pręt, równoważącą siłę zewnętrzną (I zasada dynamiki).
9EKRAN_245
Rozwiązanie:
Poruszający się przewód wraz z szynami których rezystancję zamodelowano za pomocą elementu skupionego o wartości R tworzy pętle o zmieniającej się w czasie powierzchni:
![]()
stąd strumień można przedstawić wzorem![]()
Uwzględniając prawo Faradaya (![]()
) i różniczkując strumień po czasie otrzymamy indukującą się siłę elektromotoryczną: ![]()
W obwodzie pod wpływem wyznaczonej SEM płynie prad: ![]()
Komentarz-EKRAN_245
Rezystancja szyn została podana dla pewnej chwili co oznacza, że w dłuższym okresie czasu przy przemieszczaniu się pręta należałoby uwzględnić jej zmiany.
9EKRAN_246
Na przewód z prądem w polu magnetycznym działa siła, która ma zwrot przeciwny (reguła lewej dłono) do siły zewnętrznej (zgodnej ze zwrotem v):
![]()
Moc mechaniczna dostarczona można określi ze wzoru : ![]()
Moc wydzielona na rezystancij: ![]()
Odpowiedź: Prąd płynący w obwodzie wyniósł I=24A , a moc tracona na rezystancji Pr=57.6W.
Komentarz-EKRAN_246
Zwróć uwagę, że dostarczona moc mechaniczna jest równa wydzielonej mocy elektrycznej. Bilans ten jest zachowany dzięki pominięciu sił tarcia.
9EKRAN_247
Zadanie
Obliczyć wartość maksymalną siły elektromotorycznej indukowanej w cewce złożonej z z=100 zwojów, jeżeli przebieg zmian strumienia magnetycznego przenikającego cewkę podany jest na rys. 1 a jego wartość maksymalna wynosi 2∙10-2 Wb. Założyć, że przez wszystkie zwoje cewki przenika ten sam strumień.
Komentarz-EKRAN_247
Odpowiedź: emax =100V
9EKRAN_248
Podsumowanie
Oprócz poznanych nowych praw (prawo Faradaya) i reguł (reguła Lenza) w lekcji zaprezentowano szereg przykładów z ich zastosowaniem. W niektórych przykładach wykorzystano metodę analizy magnetowodów do uproszczonego wyznaczenia indukcyjności własnej. Wprowadzono nowy element (cewkę) wobec, której stosujemy wzór Faradaya ze znakiem plus przy lewostronnym całkowaniu siły elektromotorycznej wobec strumienia wzbudzającego tą SEM. Efektem tego jest odbiornikowe zastrzałkowanie napięcia na cewce bez względu na sposób jej nawinięcia. To pozwoli w przyszłości na rysowanie cewki jako element płaski w schemacie elektrycznym.
e
d
![]()
![]()
i
e
i(t)
d
![]()
t
strzałkowanie
prawoskrętne
![]()
e
d
i
V
N
S
strzałkowanie
lewoskrętne względem strumienia wzbudzającego
![]()
![]()
i
e
e
e
i(t)
d
v
i
V
N
N
S
G
_
+
S
d
e
e
i(t)
e
e
e
i
![]()
![]()
i(t)
t
I
II
III
IV
Φ1
Φ2
I
l
I
R
R
1
a
r
dr
2
R
R1
R2
i
a
dr
r
R2
R1
R1
a
80
60
-Φmax
40
20
t[ms]
-emax
Rys.1
0
emax
Φmax
e
Φ
Φ
![]()
![]()
R
![]()
I
l
e
Rys.2a
[V]
t[ms]
0
1 2 3 4 5 6
3
2
1
-1
-2
-3
Rys.2b
uab[V]
t[ms]
0
1 2 3 4 5 6
3
2
1
-1
-2
-3
Rys.1a
uab
Φ2
e2
Φ11
e1
Rys.1b
t[ms]
1
6
Φ2
-6
-3
0
3
6
Φ [10-3Wb]
Φ1
Wyszukiwarka
Podobne podstrony:
Elektrotechnika.02.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
Elektrotechnika.11.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
Elektrotechnika.05.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
Elektrotechnika.04.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
elektrotechnika.07.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
m010p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Biochemia - kolokwium[1], Studia, Semestr III, Biochemia, Wykłady
m014a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m002b, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
ZASADA ZACHOWANIA PĘDU, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
zadania mechanika 11.06.2004, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m011p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Moment siły względem punktu, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
WYKŁAD 01, STUDIA, III rok, INTERNA, Wykłady, wykłady 2006-7
TOCZNE TARCIE LUX PROTOKOL, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m009a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m013a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
więcej podobnych podstron