Wariant II - posadowienie na palach wg PN-83/B-02482

13. Określenie parametrów geotechnicznych

Parametry ustalono metodą B wg normy PN-81/B-03020, polegającą na oznaczeniu wartości parametru na postawie ustalonych zależności korelacyjnych między parametrami fizycznymi lub wytrzymałościowymi a innymi parametrami wyznaczonymi za pomocą badań polowych lub laboratoryjnych.

Zebrane wartości przedstawiono w tab. 9a i 9b:

Tabela 1		wartości charakterystyczne
warstwa gruntu		ID	IL	Ϫ^(n)	w	Ϫ '^(n)	ϕ^(n)	c^(n)	M0	E0
nr	rodzaj	[-]	[-]	[kN/m^3]	[%]	[kN/m^3]	[ş]	[kPa]	[MPa]	[MPa]
I	Gp	-	0,08	21,58	12,00	12,05	17,00	22,00	38,50	28,00
IIa	Ps	0,63	-	18,15	14,00	9,91	34,00	-	118,00	99,00
IIb	Ps	0,63	-	19,62	22,00	10,01	34,00	-	118,00	99,00
III	Pr	0,53	-	19,62	22,00	10,01	33,00	-	102,00	85,00
gr. zas.	Po	0,60	-	18,15	4,00	10,87	39,20	-	175,00	155,00
IV	T	-	0,71	-	-	9,00	9,00	-	2,50	-

Tab. 9a Wartości charakterystyczne parametrów geotechnicznych warstw gruntu

wartości obliczeniowe
Ϫmax^(r)	Ϫmin^(r)	Ϫ 'max^(r)	Ϫ 'min^(r)	ϕmax^(r)	ϕmin^(r)	cmin^(r)
1,1	0,9	1,1	0,9	1,1	0,9	0,9
23,74	19,42	13,26	10,85	18,70	15,30	19,80
19,96	16,33	10,90	8,92	37,40	30,60	-
21,58	17,66	11,01	9,01	37,40	30,60	-
21,58	17,66	11,01	9,01	36,30	29,70	-
19,96	16,33	11,95	9,78	43,12	35,28	-
-	-	9,90	8,10	9,90	8,10	-

Tab. 9b Wartości obliczeniowe parametrów geotechnicznych warstw gruntu

Obliczenia dla warstwy I - gliny piaszczystej (geneza C)

Stan gruntu I_L = 0,08

ρ_s = 2,67 t/m³ - wartość odczytana z normy PN-81/B-03020 - tabl. 2, str. 12

γ_s = ρ_s * g = 2,67 * 9,81 = 26,19 kN/m³

w_n = 12 % - wartość odczytana z normy PN-81/B-03020 - tabl. 2, str. 12

ρ = 2,2 t/m³ - wartość odczytana z normy PN-81/B-03020 - tabl. 2, str. 12

γ⁽ⁿ⁾ = ρ * g = 2,2 * 9,81 = 21,58 kN/m³ , gdzie g - przyspieszenie ziemskie

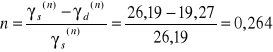
- wartość odczytana z normy PN-81/B-03020 - rys. 4, str. 13

c_(n) = 22 kPa - wartość odczytana z normy PN-81/B-03020 - rys. 5, str. 13

c_min^(r) = c_(n) * γ_m = 22 * 0,9 = 19,8 kPa

M₀ = 38,5 MPa -wartość odczytana z normy PN-81/B-03020 - rys. 7b, str. 17

E₀ = 28 MPa -wartość odczytana z normy PN-81/B-03020 - rys. 7a, str. 17

Piasek średni zalegający powyżej ZWG przyjęto jako wilgotny, poniżej jako mokry.

Jako grunt zasypowy przyjęto pospółkę (P_o) o I_D = 0,60.

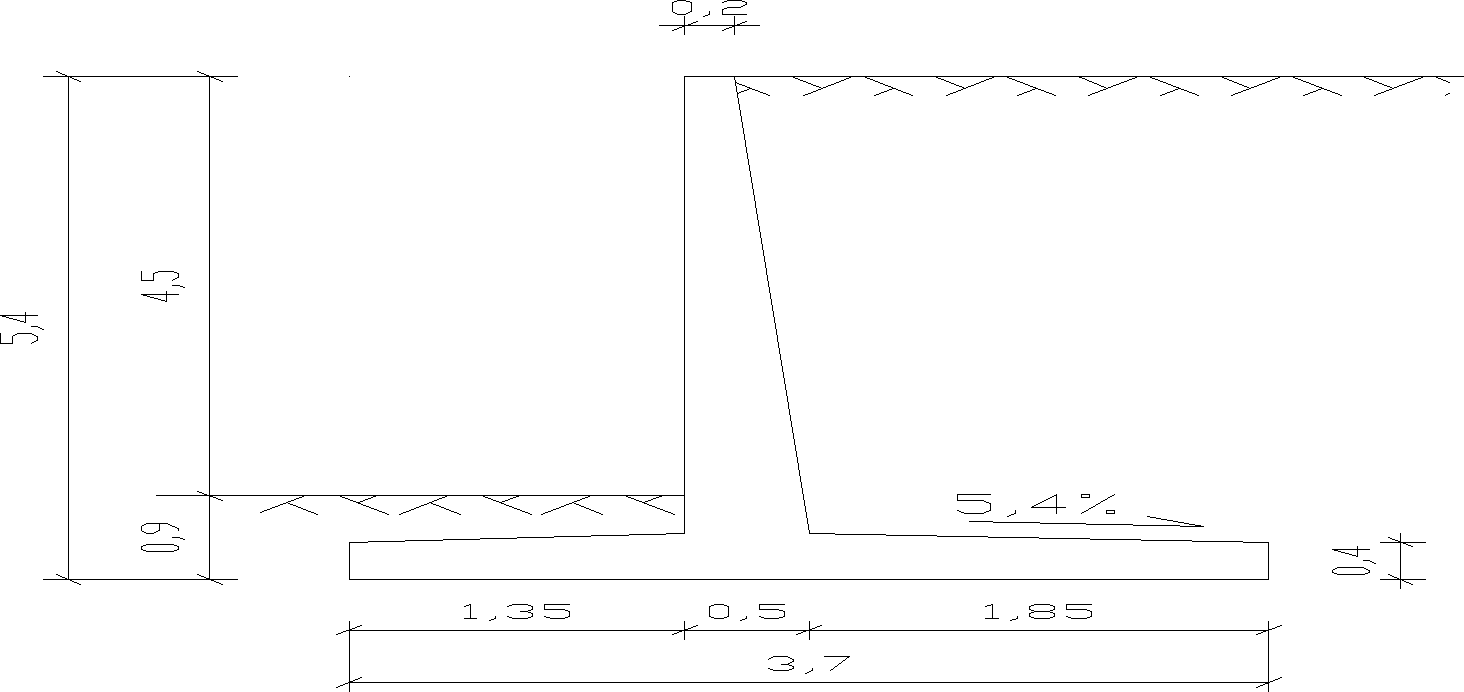
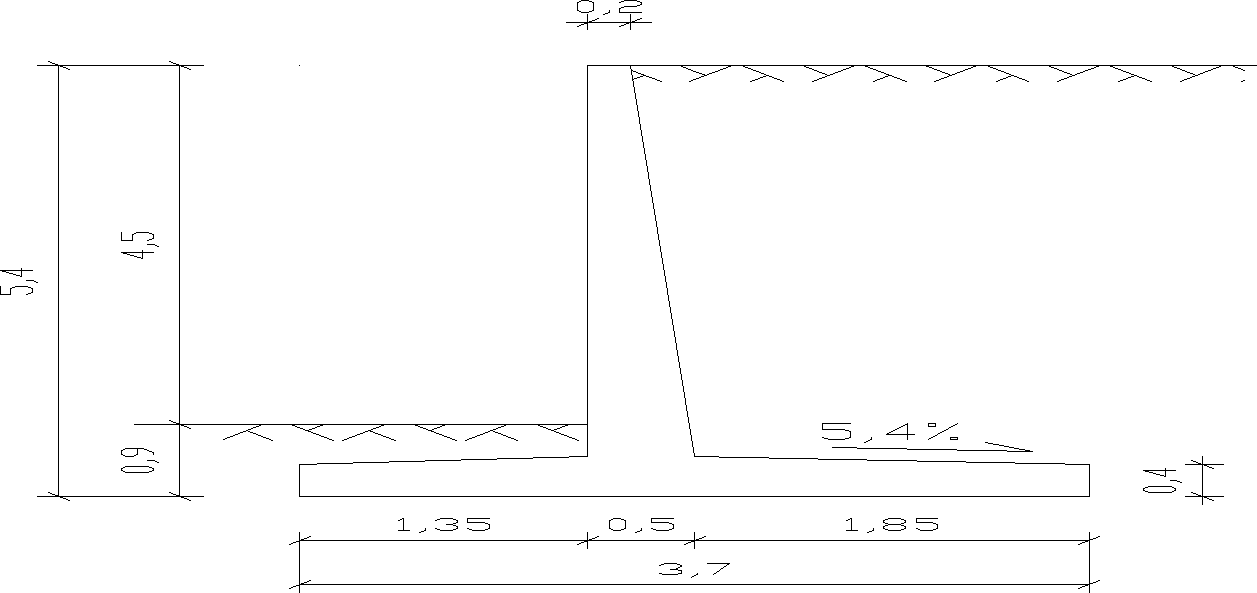
14. Przyjęcie wymiarów ściany oporowej

Projektowana ściana jest ścianą kątową.

Rys.10 Wymiary ściany oporowej (wymiary w [m])

15. Zebranie obciążeń

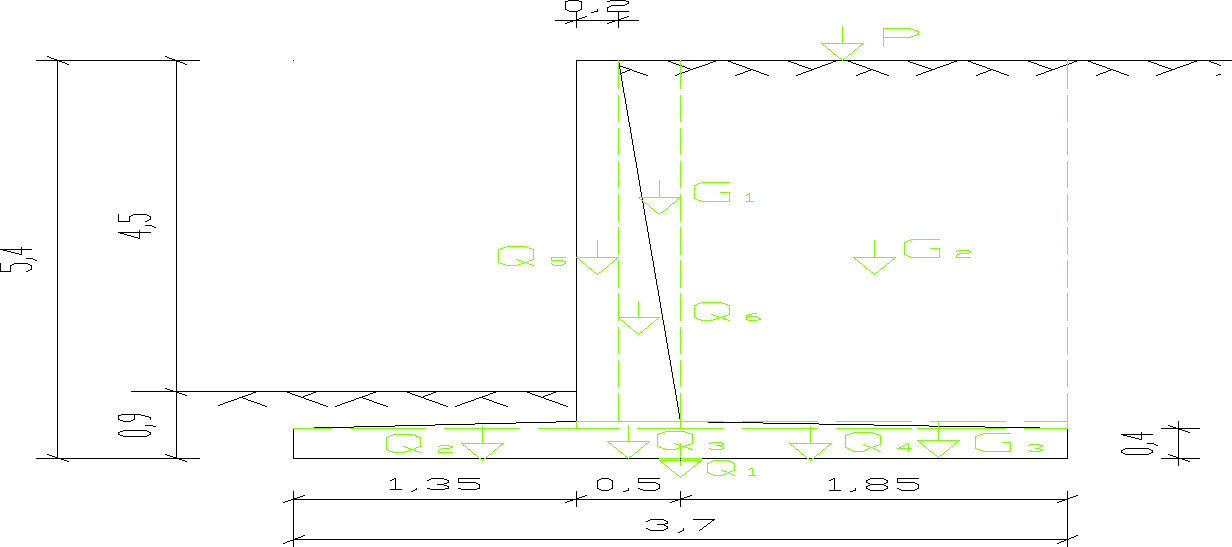
15.1 Obciążenia pionowe

Obciążenia ściany oporowej zebrano na 1 mb konstrukcji.

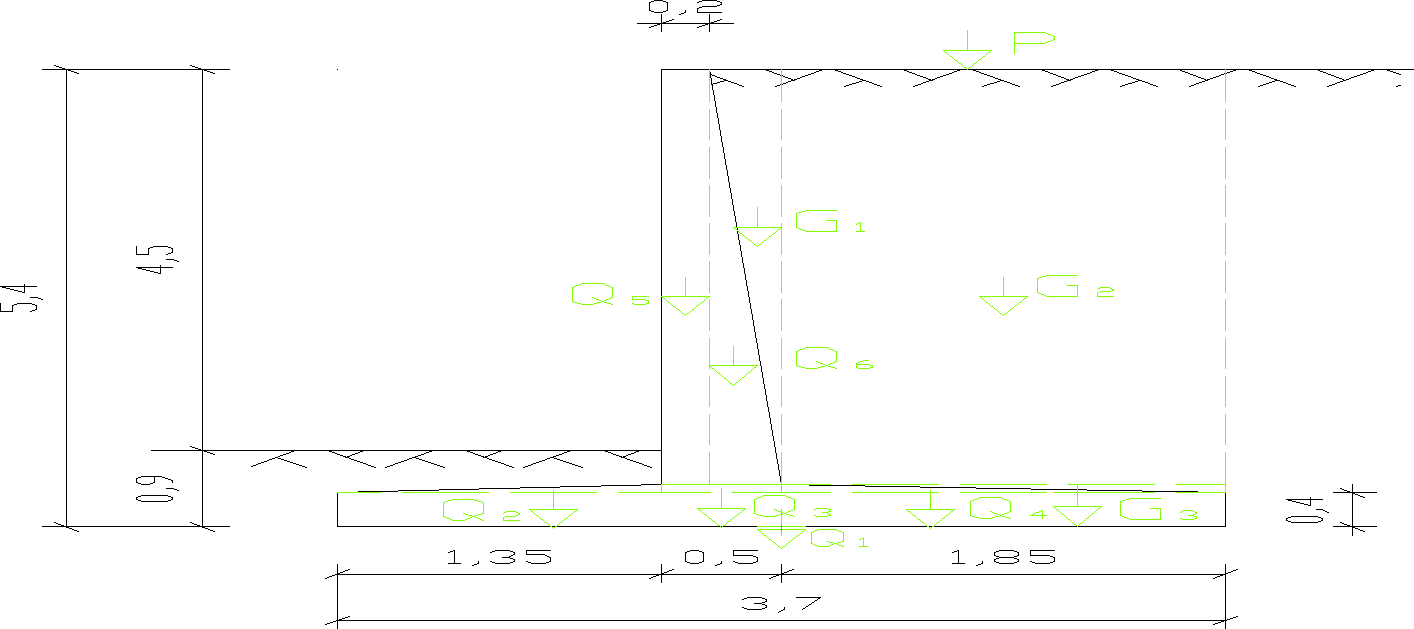
Rys. 11 Wypadkowe sił pionowych działających na ścianę oporową

Obciążenia od konstrukcji - ciężar własny elementów ściany (Q).

Wartości charakterystyczne ciężaru własnego ściany, wykonanej z żelbetu γ_ż = 25 kN/m.

Wartości współczynnika obciążeń: ɣ_f = 1,1 (0,9).

Q₁ = 3,7 * 0,4 * 25 = 37 kN/m

Q₂ = 0,5 * 1,35 * 0,1 * 25 = 1,7 kN/m

Q₃ = 0,5 * 0,1 * 25 = 1,25 kN/m

Q₄ = 0,5 * 1,85 * 0,1 * 25 = 2,3 kN/m

Q₅ = 0,2 * 4,9 * 25 = 24,5 kN/m

Q₆ = 0,5 * 4,9 * 0,3 * 25 = 18,4 kN/m

Obciążenie od gruntu (G) - nad odsadzkami

W zebraniu obciążeń pominięto ciężar gruntu na podsadzce po stronie niższego

naziomu.

Wartości charakterystyczne ciężaru objętościowego gruntu określono na podstawie

normy PN-81/B-03020.

Wartości współczynników obciążeń do określenia wartości obliczeniowych dla gruntu zasypowego bez kontroli zagęszczenia ɣ_f = 1,2 (0,8).

G₁ = 0,5 * 0,3 * 4,9 * 18,15 = 13,3 kN/m γ_Ps = 18,15 kN/m

G₂ = 1,85 * 4,9 * 18,15 = 164,52kN/m

G₃ = 0,5 * 1,85 * 0,1 * 18,15 = 1,7 kN/m

Obciążenie naziomu (P)

Wartości charakterystyczne obciążenia naziomu podano w temacie.

Wartości współczynników obciążeń ɣ_f do określenia wartości obliczeniowych dla obciążenia naziomu powyżej 5 kN/m² ɣ_f = 1,2 (0,9).

P = 15 * 2,15 = 32,25 kN/m

Wartości obciążeń pionowych, zebrano i przedstawiono w tab. 10:

obciążenie	wartości charakterystyczne			wartości obliczeniowe
	X^(n)	r0(X)	M0(X)	Ϫfmax	Xmax^(r)	M0(Xmax)	Ϫfmin	Xmin^(r)	M0(Xmin)
		[kN/m]	[m]	[kNm/mb]	[-]	[kN/m]	[kNm/mb]	[-]	[kN/m]	[kNm/mb]
Q1	37	0	0,00	1,1	40,70	0,00	0,9	33,30	0,00
Q2	1,7	0,95	1,62	1,1	1,87	1,78	0,9	1,53	1,45
Q3	1,25	0,25	0,31	1,1	1,38	0,34	0,9	1,13	0,28
Q4	2,3	-0,62	-1,43	1,1	2,53	-1,57	0,9	2,07	-1,28
Q5	24,5	0,4	9,80	1,1	26,95	10,78	0,9	22,05	8,82
Q6	18,4	0,2	3,68	1,1	20,24	4,05	0,9	16,56	3,31
G1	13,3	0,1	1,33	1,2	15,96	1,60	0,8	10,64	1,06
G2	164,5	-0,93	-152,99	1,2	197,40	-183,58	0,8	131,60	-122,39
G3	1,7	-1,23	-2,09	1,2	2,04	-2,51	0,8	1,36	-1,67
P	32,25	-0,78	-25,16	1,2	38,70	-30,19	0,9	29,03	-22,64
∑	296,9		-164,92		347,77	-199,30		249,26	-133,05

Tab. 10 Wartości charakterystyczne i obliczeniowe obciążenia pionowego

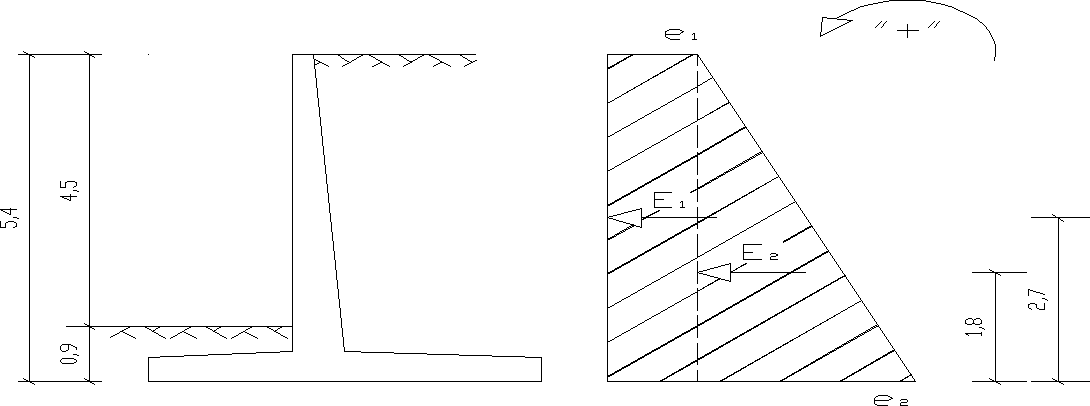
15.2 Obciążenie poziome - parcie gruntu

Przyjęto parcie pośrednie.

Grunt zasypowy - pospółka: I_D = 0,60, ϕ⁽ⁿ⁾ = 39,2º

I_S = 0,855 + 0,165 * I_D = 0,855 + 0,165 * 0,6 = 0,954 wskaźnik zagęszczenia

K_a = tg²(45 -
) = tg²(45 - 19,6) = 0,225 współczynnik parcia czynnego

K₀ = [0,5 - ξ₄ + (0,1 + 2*ξ₄)(5*I_S - 4,15)*ξ₅](1+0,5*tgε) =

[0,5 - 0,1 + (0,1 + 2*0,1)(5*0,954 - 4,15)*0,9] = (0,4 + 0,167) = 0,567

K₀ = 1 - sinϕ = 1 - sin39,2º = 0,368

ξ_4, ξ₅ - współczynniki zależne od sposobu zagęszczenia gruntu, odczytane z normy

PN-81/B-03010

ξ₄ = 0,1

ξ₅ = 0,9

K₀ = max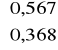
= 0,567

K₁ =
=
=0,273

Wartości parcia jednostkowego

e₁ = p * K₁ = 15 * 0,273 = 4,1 kPa

e₂ = (p + H*γ)*K₁ = (15 + 5,4 * 18,15)*0,273 = 30,85 kPa

Wypadkowe parcia

E₁ = e₁ * H = 4,1 * 5,4 = 22,14 kN/mb

E₂ = 0,5 * (e₂ - e₁) * H = 0,5 * (30,85 - 4,1) * 5,4 = 72,23 kN/mb

Długość ramienia, na którym działa pozioma siła wypadkowa parcia gruntu

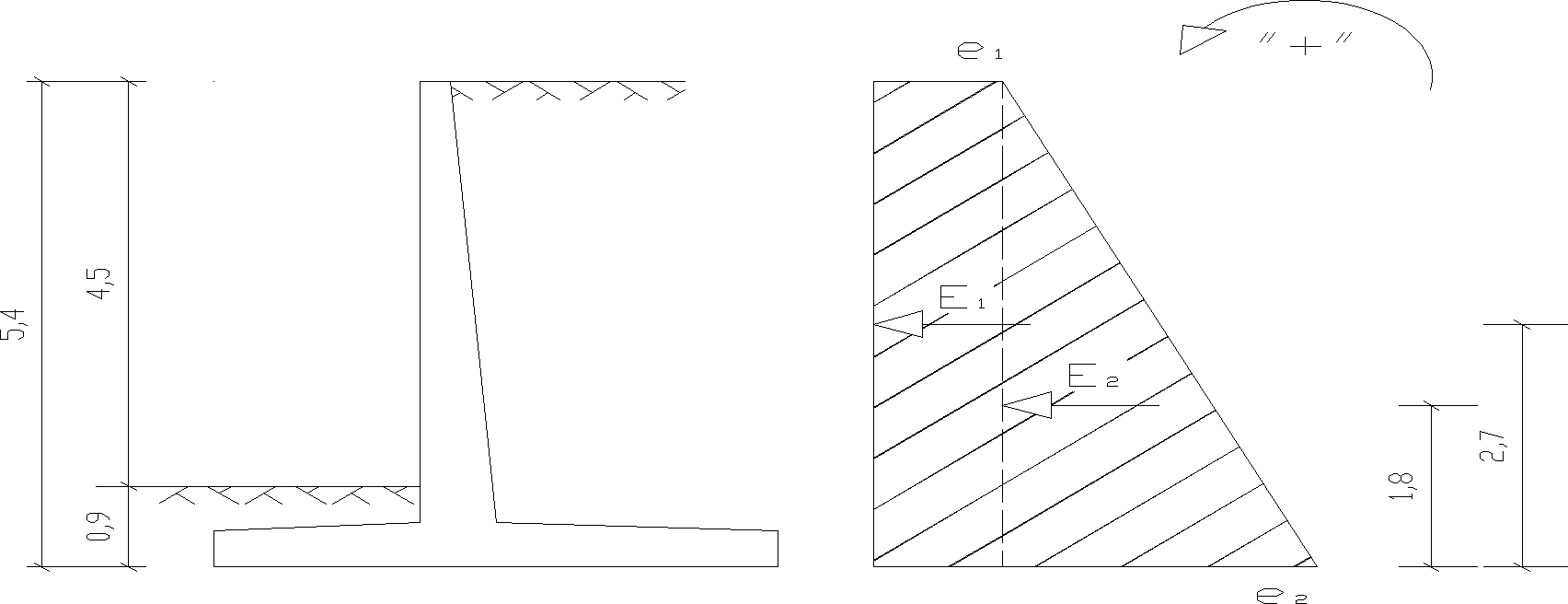
r₀₁ = 0,5 * H = 0,5 * 5,4 = 2,7 m

r₀₂ = 1/3 * H = 1/3 * 5,4 = 1,8 m

Rys. 12 Wypadkowe siły poziome działające na ścianę oporową.

Odpór gruntu przed ścianą ze względów bezpieczeństwa pominięto.

W zbieraniu obciążeń obliczeniowych poziomych uwzględniono tylko wartości

maksymalne ponieważ parcie minimalne nie daje wartości niekorzystniejszych.

obciążenie	wartości charakterystyczne			wartości obliczeniowe
	E^(n)	r0(E^(n))	M0(E^(n))	Ϫfmax	Emax^(r)	M0(Emax)
		kN/mb	m	kNm/mb		kN/mb	kNm/mb
E1	22,14	2,7	59,78	1,2	26,57	71,73
E2	72,23	1,8	130,01	1,2	86,68	156,02
∑	94,37		189,79		113,24	227,75

Tab.11 Wartości charakterystyczne i obliczeniowe obciążenia poziomego

16. Sprawdzenie wymiarów ściany

16.1 Sprowadzenie wypadkowej obciążeń do podstawy fundamentu

Wartości charakterystyczne X^(n), E⁽ⁿ⁾

e_B =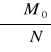
=
=
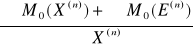
= 0,084 m

0,084 m
warunek spełniony

Wartość siłt wypadkowej

W=
=
= 311,4 kN/m

wartość kąta nachylenia wypadkowej do pionu

sinα =
=
= 0,304 => α = 17º41'

Wartości obliczeniowe X_max^(r), E_max^(r)

N_r = ∑ X_max^(r) = 347,77 kN/m

T_r = ∑ E_msx^(r) = 113,24 kN/m

e_B =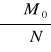
=
=
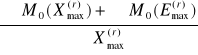
= 0,082m

0,082 m
warunek spełniony

Wartości obliczeniowe X_min^(r), E_max^(r)

e_B =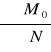
=
=
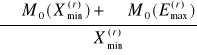
= 0,38 m

0,38 m
warunek spełniony

17. Przyjęcie pali

Zastosowano pale Vibrex o średnicy 0,508 m . Są to pale wbijane za pomocą młotów hydraulicznych lub spalinowych. Mają zamkniętą podstawę tworzącą tzw. but stalowy, która podczas wyciągania przy pomocy wyciągarki i wibratora jest tracona. Pale wykonywane tą techniką mają powiększoną średnicę podstawy i pobocznicy w rejonie podstawy. Charakteryzują się bardzo dużą nośnością oraz bardzo małymi osiadaniami. Zazwyczaj stosowane są w gruntach luźnych, średniozagęszczonych i zagęszczonych.

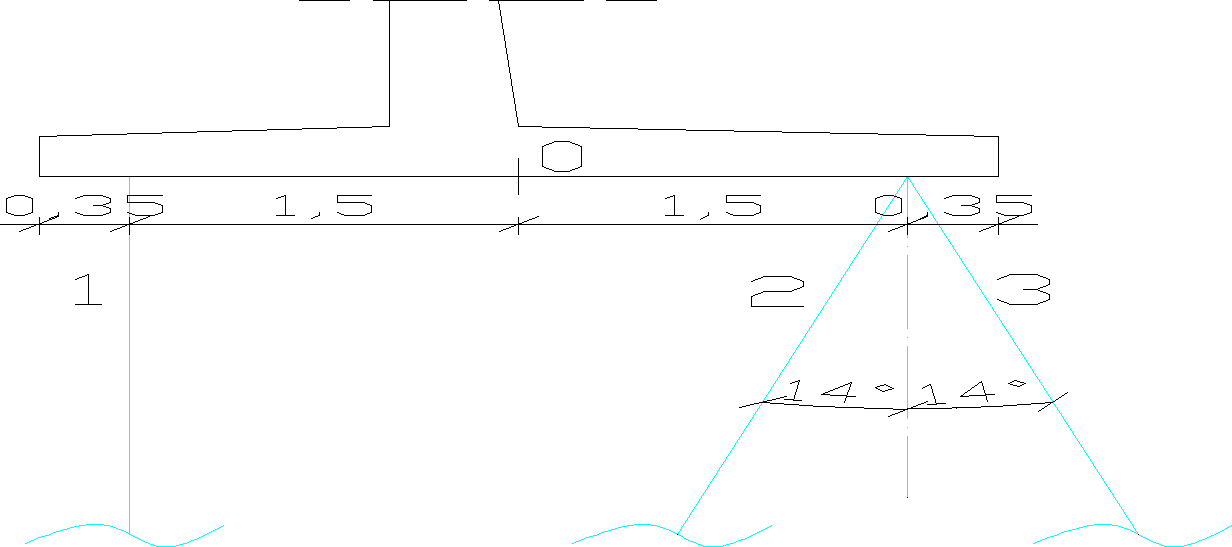
18. Układ pali w przekroju ściany

Pale są rozmieszczone w układzie kozłowym.. Pale rzędu 1 i 2 są palami wciskanymi, pale rzędu 3 palami wyciąganymi. Nachylenie pali ukośnym wynosi 4 : 1. Minimalne zagłębienie w gruncie nośnym wynosi 1,52 m. Odległość osi pala od krawędzi fundamentu

wynosi 0,35 m.

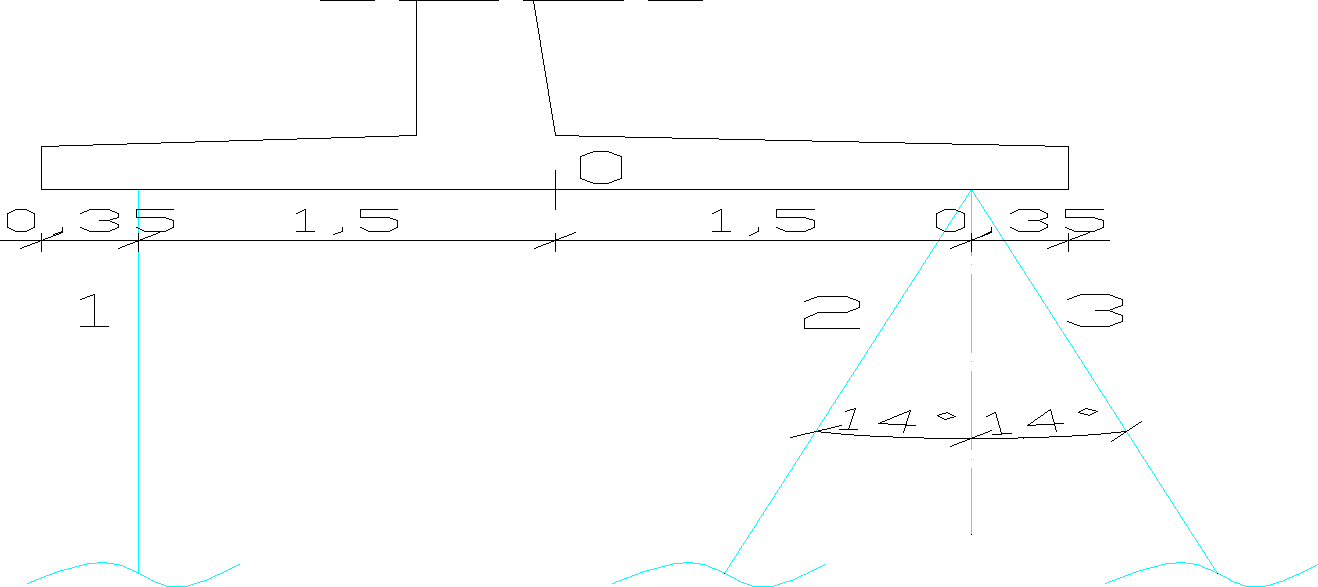
Rys. 13 Układ pali w przekroju ściany

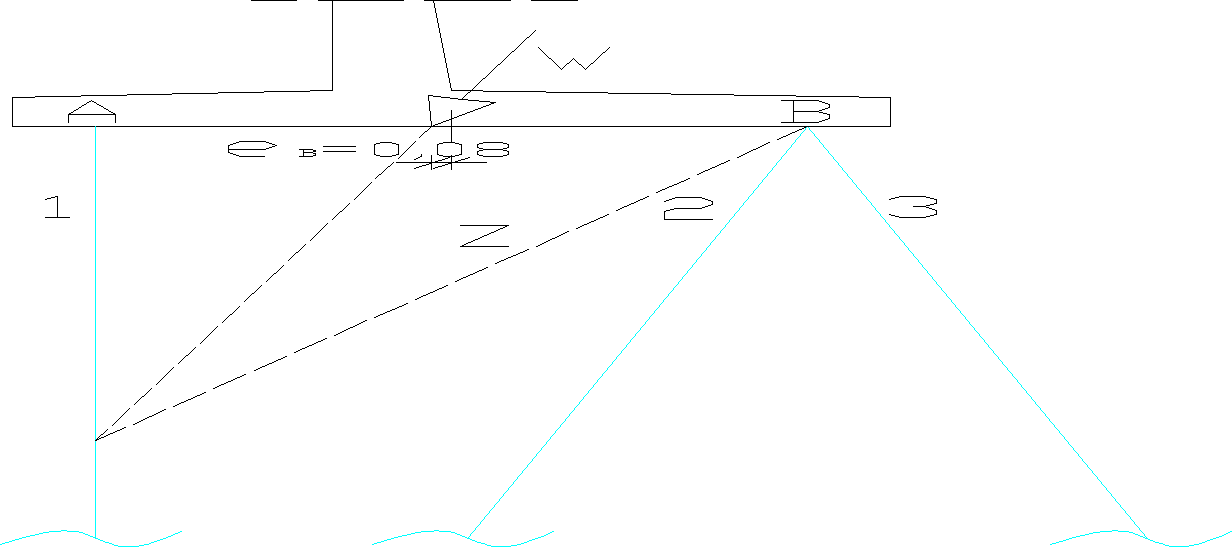
19. Wyznaczenie siły w palach

19.1 Wyznaczenie siły w palach metodą Cullmana (metoda graficzna)

Wartości obliczeniowe X_max^(r), E_max^(r)

e_B =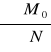
=
=
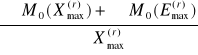
= 0,08m

wartość kąta nachylenia wypadkowej do poziomu

sinα =
=
= 0,951 => α = 72º

skala: 1 jednostka = 50 kN/m

W = 365,7 kN/m / 50 kN/m = 7,3 jednostki

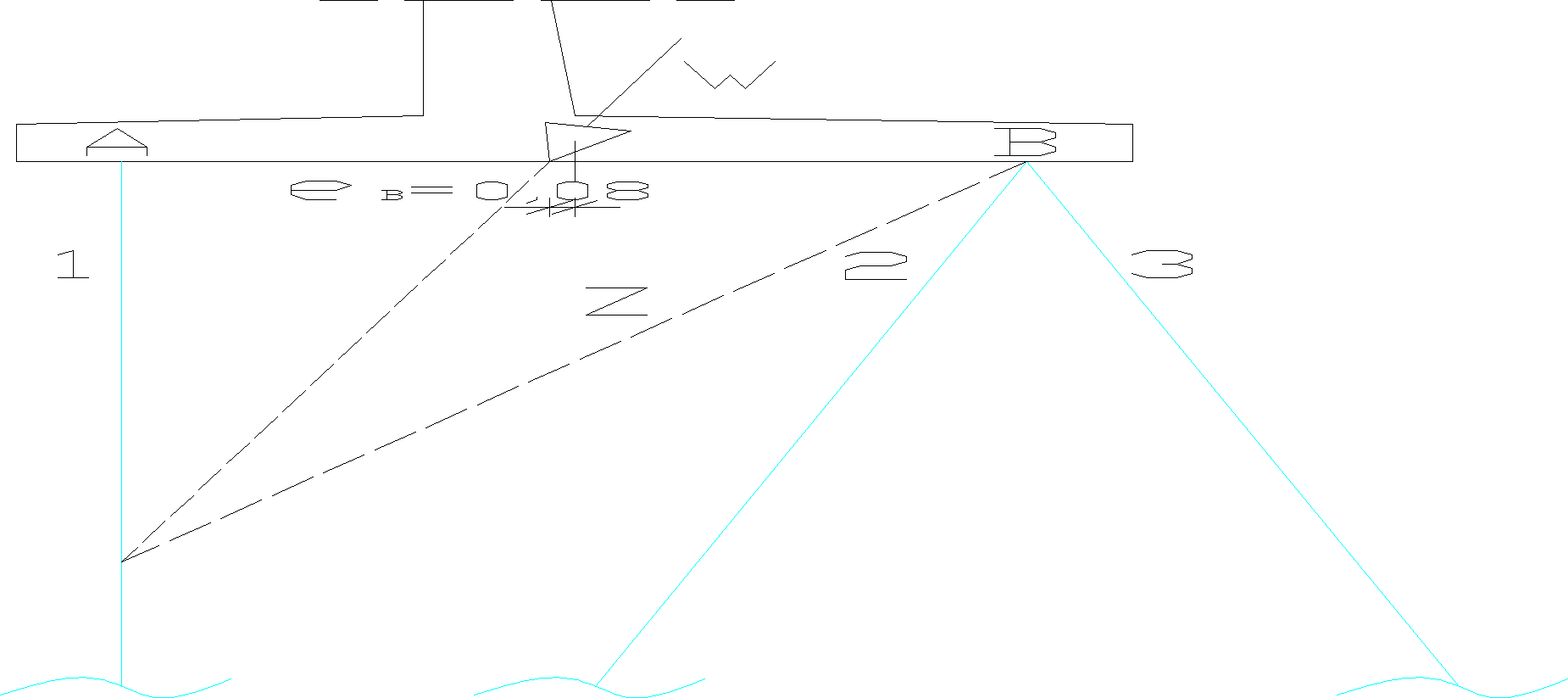
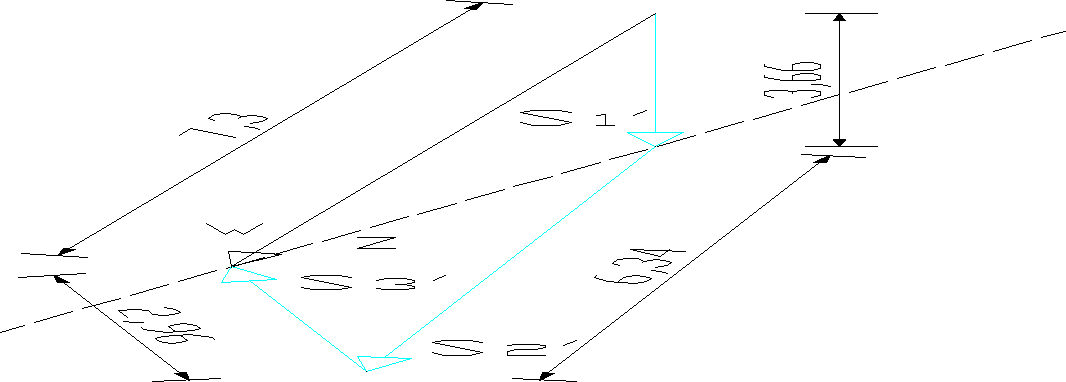
Rys. 14a. Wyznaczanie siły w palach metodą Cullmana

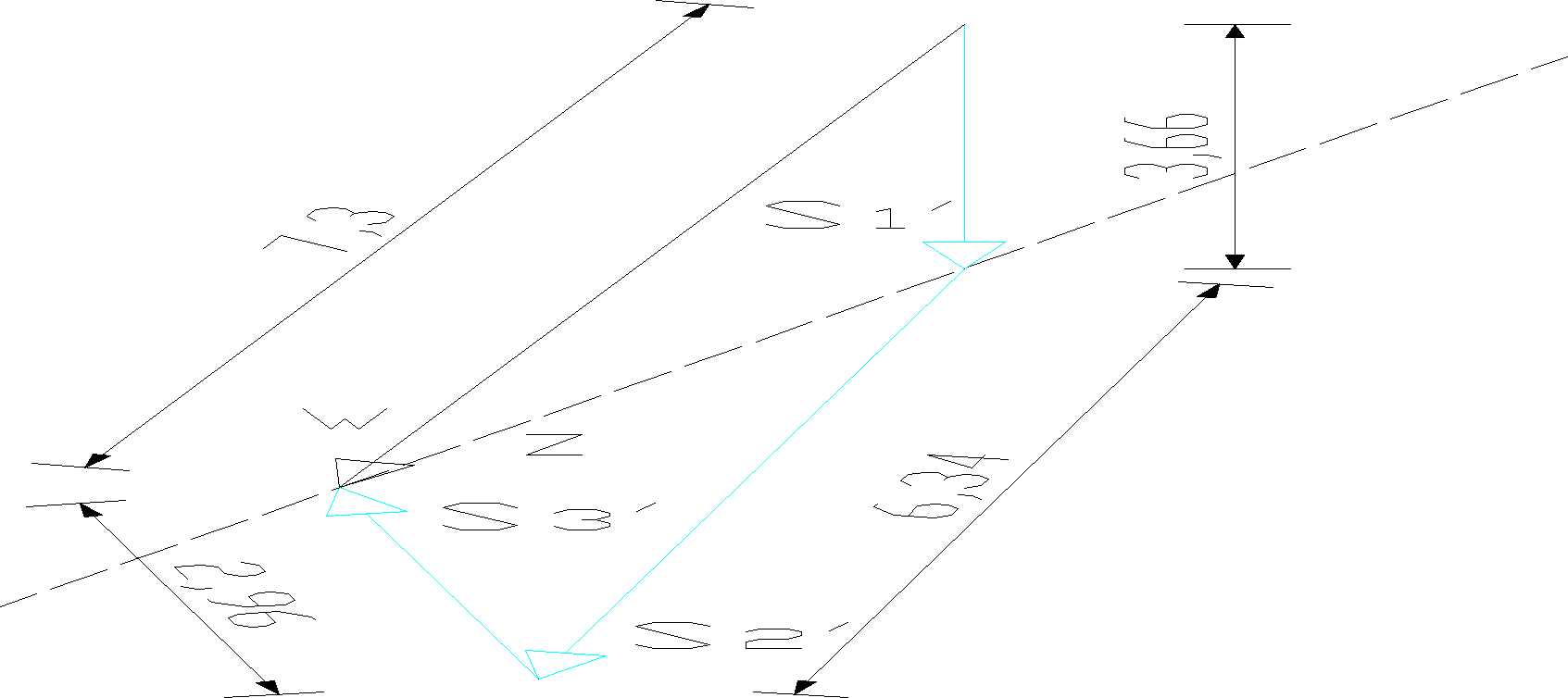
Rys. 14b. Wyznaczanie siły w palach metodą Cullmana

Obliczenia

S₁' = 3,66 * 50 = 183 kN/m

S₂`= 6,34 * 50 = 317 kN/m

S₃' = 2,96 * 50 = 148 kN/m

19.2 Wyznaczenie siły w palach metodą analityczną

∑ M_B = 0 => S₁*AB - ∑V*(e_B +
) = 0 ∑ V = 347,77kN/m

AB = 3 m

S₁*3 - 347,77*(0,08 +3/2) = 0

S₁ = 183,16 kN/m

∑ M_A = 0 => (-S₁*cosβ + S₃*cosβ)*AB + ∑V*(
- e_B) = 0

cosβ = cos 14º = 0,970

sinβ = sin 14º = 0,242

(-S₂*0,970 + S₃*0,970)*3 + 347,77*(1,5 - 0,08) = 0

-2,91*S₂ + 2,91*S₃ + 493,8 = 0

S₃ = S₂ - 169,7

∑ P_x = 0 S₂*sinβ + S₃*sinβ - ∑ H = 0 ∑ H = 113,24 kN/m

S₂*0,242 + S₃*0,242 - 113,24 = 0

S₂*0,242 + (S₂ - 169,7)*0,242 - 113,24 = 0

S₂ =
= 318,8 kN/m

S₃ = 318,8 - 169,7 = 149,1 kN/m

20. Przyjęcie planu palowania

Długość sekcji dylatacyjnej wynosi L = 14m. W jednym rzędzie znajduje się 7 pali (n = 7).

Odległość osiowa między palami wynosi 2m.

Plan palowania znajduje się na rys. 3 w załączniku.

21. Wyznaczenie sił w pojedynczym palu

S_i =

- siła w palu wyznaczona metodą Cullmana

L = 14m - długość sekcji dylatacyjnej

n = 7 - liczba pali w rzędzie

S₁ =
= 366 kN

S₂ =
= 634 kN

S₃ =
= 296 kN

Sprawdzenie stanu granicznego nośności

Sprawdzenie warunku:

Q_r ≤ m*N

gdzie:

N - nośność pala pojedynczego i w grupie

Q_r = S₁, S₂, S₃ - siła w pojedynczym palu (wartość obliczeniowa)

m - współczynnik korekcyjny, dla układu 3 pali m = 0,9

22. Nośność pala pojedynczego pojedynczego uwzględnieniem tarcia negatywnego

22.1 Nośność pala pojedynczego

Nośność pala wciskanego:

Nośność pala wyciąganego: N^w = N_s = ∑S^w_i * t_i^(r) * A_si

Nośność podstawy :

Nośność pobocznicy: N_s = ∑S_si * t_i^(r) * A_si

Tarcie negatywne: T_n = N_s = ∑S_si * t_i^(r) * A_si

S_p, S_si, S^w  - współczynniki technologiczne zależne od pala odczytane z tabl. 4, str. 9

PN-83/B-02482

A_p ­- pole podstawy

A_s - pole pobocznicy pala

q^(r) - jednostkowa obliczeniowa wytrzymałość gruntu pod podstawą pala

t^(r) - jednostkowa obliczeniowa wytrzymałość gruntu wzdłuż pobocznicy

Obliczenie pola podstawy z uwzględnieniem współczynnika zwiększającego pole 1,25

A_p = 1,25 *
= 0,253 m²

Obliczenie pola pobocznicy dla 1 mb pala:

A_s =
= 3,14 * 0,508 * 1 = 1,595 m²

Wyznaczone współczynniki S_p, S_si, S^w   przedstawiono w tabelach 12a i 12b.

Wyznaczenie głębokości krytycznej h_ci:

D_i - średnica pala, D_i = 0,508 m

D_o - średnica miarodajna pala, D_o = 0,4 m

h_ci = h_c

h_ci = 10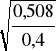
= 11,27 m

Określenie poziomu interpolacji h_z::

Wysokość h_z mierzona jest od spągu warstwy torfu

h_z =
* (∑γ_i*h_i)

γ_Pr = 10,01 kN/m³

∑γ_i * h_i = 21,58*1,5 + 18,15*1,2 + 10,01*1,9 + 9,0*5,4 = 121,77 kN/m²

h_z =
*121,77 = 7,9 m

Wyznaczenie q_max⁽ⁿ⁾ (jednostkowego charakterystycznego granicznego oporu gruntu pod podstawą pala) dla piasku grubego o I_D = 0,53 poprzez interpolacje liniową wartości z tabl. 1 str. 6 PN-83/B-02482

I_D = 0,67 I_D = 0,33 => ΔI_D = 0,34

q_max = 3600 kPa q_max = 2150 kPa => Δq_max = 1450 kPa

0,34 - 1450

0,01 - X

X = 42,65 kPa

q_max⁽ⁿ⁾ = 2150 + (0,53 - 0,33) * 42,65 = 3003 kPa

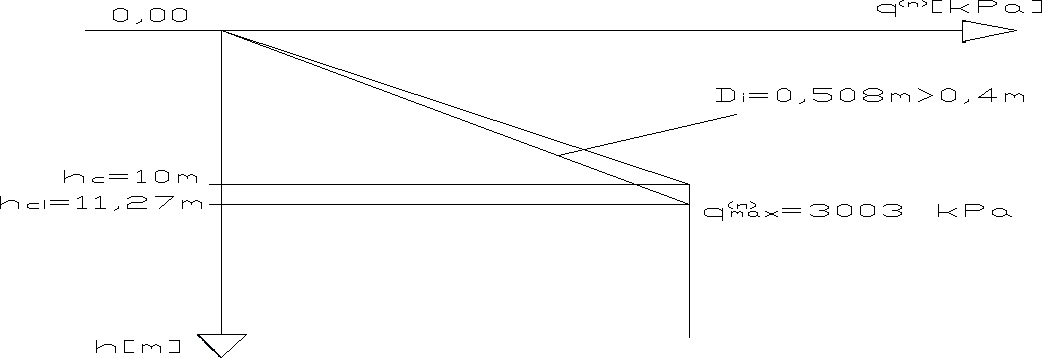
Rys. 15. Wykres zależności q od miąższości warstwy

Wyznaczenie t_max⁽ⁿ⁾ (jednostkowego charakterystycznego granicznego oporu gruntu wzdłuż pobocznicy pala) oraz t_max^(r) dla poszczególnych warstw poprzez interpolacje liniową wartości z tabl. 2 str. 7 PN-83/B-02482

Obliczenie t_max^(r) według wzoru:

t_max^(r) = γ_m * t_max⁽ⁿ⁾

gdzie γ_m jest współczynnikiem materiałowym, który dla tarcia pozytywnego wynosi γ_m = 0,9, tarcia negatywnego γ_m = 1,1, dla torfu γ_m = 1,0

Warstwa 4 - piasek gruby (warstwa nośna) o I_D=0,53

t⁽ⁿ⁾ = 62,88 kPa

γ_m = 0,9 (tarcie pozytywne)

t_max(r) = 0,9*62,88 = 56,59 kPa

Warstwa 3 - torf o I_L=0,71

t_max⁽ⁿ⁾ = 8,0 kPa

γ_m = 1,0 (tarcie negatywne)

t_max^(r) = 1,0*,0 = 8,0 kPa

Warstwa 2 - piasek średni o I_D=0,63

t_max⁽ⁿ⁾ = 70,82 kPa

γ_m = 1,1 (tarcie negatywne)

t_max^(r) = 1,1*70,82 = 77,9 kPa

Warstwa 1 - glina piaszczysta o I_L=0,08

t_max⁽ⁿ⁾ = 46 kPa

γ_m = 1,1 (tarcie negatywne)

t_max^(r) = 1,1*46 = 50,6 kPa

Wartości charakterystyczne i obliczeniowe, oraz wartości współczynników materiałowych zebrano i przedstawiono w tabelach 12a i 12b.

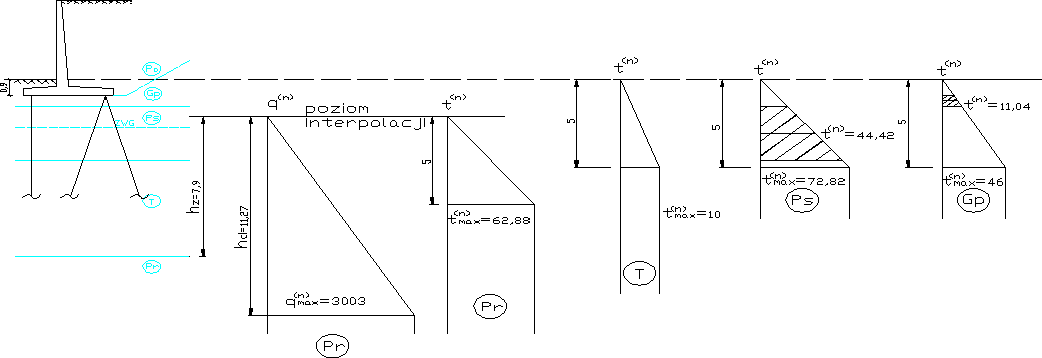
Rys. 16 Interpolacja oporów gruntu wzdłuż pobocznicą i pod podstawą pala w przypadku gruntów uwarstwionych

22.2 Nośność pala w grupie

Pale wciskane

Warunek nośności pala w grupie:

Q_r ≤ m*N_tg

gdzie m = 0,9

Nośność pala wciskanego w grupie:

N_tg = N_p + m₁*N_s - T_n

gdzie:

m₁ - współczynnik redukcyjny zależny od r/R, określany na podstawie tabl. 8 str.

13 normy PN-83/B-02482

r - najmniejsza osiowa odległość między palami wciskanymi

R - zasięg strefy naprężeń naprężeń gruncie wokół pala R = D/2 + ∑h_i*tgα_i

h_i - miąższość warstwy, przez którą przechodzi pal (uwzględniamy tylko

długość w gruncie nośnym)

α_i - kąt, pod którym rozchodzą się naprężenia wokół pala, zależny od rodzaju

gruntu, określany na podstawie tabl. 7 str. 13 normy palowej

Powyższe wielkości oraz obliczenia zebrano i przedstawiono w tabeli 12a.

Pale wyciągane

Q_r ≤ m*N_wg

gdzie m = 0,9

Nośność pala wyciąganego w grupie

N_wg = m₁*N_s

gdzie:

m₁ - współczynnik redukcyjny, zmniejszający nośność pali pracujących w grupie,

określany na podstawie tabl. 8 str. 13 normy palowej, zależny od

r - osiowa odległość między palami wyciąganymi,

R - zasięg strefy naprężeń w gruncie wokół pala:

R = D/2 + 0,1*h

h - miąższość warstwy, przez którą przechodzi pal (uwzględniamy tylko długość

długość gruncie nośnym)

Powyższe wielkości oraz obliczenia zebrano i przedstawiono w tabelach 12a i 12b.

Pale wciskane

Długość	Rzędna	Warstwa	Nośność podstawy (Ap = 0,253 m^2)				Nośność pobocznicy (As(1 mb) = 1,596 m^2)
pala			geotechniczna	Sp	q^(n)	Ϫm	Np = Sp*Ap*q^(n)*Ϫm	Ssi	hi	ti^(n)	Ϫm	Nsi = Ssi*hi*Asi*ti^(n)*Ϫm	Tn = ∑Nsi	Ns = ∑Nsi
[ m ]	[m p.p.t.]		[-]	[kPa]	[-]	[kN]	[-]	[m]	[kPa]	[-]	[kN]	[kN]	[kN]
	-0,90	Poziom posadowienia	-	-	-	-	-	-	-	-	-	-	-
	-1,50	Gp	-	-	-	-	0,9	0,6	-11,04	1,1	-10,47	-10,47	-
	-4,60	Ps	-	-	-	-	1,1	3,1	-44,42	1,1	-265,92	-276,39	-
	-10,00	T	-	-	-	-	0,9	5,4	-10	1	-77,57	-353,96	-
11,00	-11,90	Pr	1,4	2611,30	0,9	832,43	1,1	1,9	62,88	0,9	188,77	-353,96	188,77
12,00	-12,90	Pr	1,4	2877,76	0,9	917,37	1,1	1,0	62,88	0,9	99,35	-353,96	288,12
13,00	-13,90	Pr	1,4	3003,00	0,9	957,30	1,1	1,0	62,88	0,9	99,35	-353,96	387,48
14,00	-14,90	Pr	1,4	3003,00	0,9	957,30	1,1	1,0	62,88	0,9	99,35	-353,96	486,83

Nośność pala poj.		Strefy naprężeń					Nośność pala w grupie
Nt = Np + Ns -Tn	m*Nt	tgαi	r	Ri = D/2 + ∑hi*tgαi	r/Ri	m1	Ntg = Np + m1*Ns - Tn	m*Ntg
[kN]	[kN]	[-]	[m]	[m]			[kN]	[kN]
-	-	-	-				-	-
-	-	-	-				-	-
-	-	-	-				-	-
-	-	-	-				-	-
667,24	600,52	0,105	1,69	0,4535	3,73	1,00	667,24	600,52
851,54	766,39	0,105	1,60	0,5585	2,86	1,00	851,54	766,39
990,82	891,73	0,105	1,50	0,6635	2,26	1,00	990,82	891,73
1090,17	981,15	0,105	1,39	0,7685	1,81	0,95	1065,83	959,25

Tab.12a Zestawienie obliczeń nośności pali wciskanych

Pale wyciągane - Tab 12b . Zestawienie obliczeń nośności pali wyciąganych

Długość	Rzędna	Warstwa	Nośność pobocznicy (As(1 mb) = 1,436 m^2)						Nośność pala poj.
pala			geotechniczna	S^wi	hi	ti^(n)	Ϫm	Nsi = S^wi*hi*Asi*ti^(n)*Ϫm	Ns = ∑Nsi	N^w = Ns	m*N^w
[ m ]	[m p.p.t.]		[-]	[m]	[kPa]	[-]	[kN]	[kN]	[kN]	[kN]
	-0,90	Poziom posadowienia	-	-	-	-	-	-	-	-
	-1,50	Gp	0,6	0,6	11,04	0,9	5,14	5,14	-	-
	-4,60	Ps	0,6	3,1	44,42	0,9	106,78	111,92	-	-
	-10,00	T	0,6	5,4	0	0,9	0,00	111,92	-	-
11,00	-11,90	Pr	0,6	1,9	62,88	0,9	92,64	204,56	204,56	184,10
12,00	-12,90	Pr	0,6	1,0	62,88	0,9	48,76	253,32	253,32	227,99
13,00	-13,90	Pr	0,6	1,0	62,88	0,9	48,76	302,08	302,08	271,87
14,00	-14,90	Pr	0,6	1,0	62,88	0,9	48,76	350,84	350,84	315,75
15,00	-15,90	Pr	0,6	1,0	62,88	0,9	48,76	399,60	399,60	359,64

Strefy naprężeń r = 2 m			Nośność pala w grupie
Ri = D/2 + ∑0,1*hi	r/Ri	m1	N^wg = m1*Ns	m*N^wg
[m]	[-]	[-]	[kN]	[kN]
			-	-
			-	-
			-	-
			-	-
0,444	4,50	1,00	204,56	184,10
0,544	3,68	1,00	253,32	227,99
0,644	3,11	1,00	302,08	271,87
0,744	2,69	1,00	350,84	315,75
0,844	2,37	1,00	399,60	359,64

Warunek nośności pala wciskanego w grupie (na podstawie tabeli):

Pal 1 Q_r = S₁ = 366 kN

366 kN ≤ 600,52 kN → długość pala 1: L = 11 m

Pal 2 Q_r = S₂ = 634 kN

634 kN ≤ 766,39 kN → długość pala 2: L = 12 m

Sprawdzenie warunku dla pali o uśrednionej długości pala

średnia długość pala:
= 12,5 m → r = 1,55 m → m₁ = 1,0

współczynnik m₁ w dalszym ciągu równy 1,0, nośności pali się nie zmienią → warunek spełniony

Warunek nośności pojedynczego pala wciskanego

Pal 1 o długości L = 11m Q_r = S₁ = 366 kN

366 kN ≤ 600,52 kN

Pal 2 o długości L = 12m Q_r = S₂ = 634 kN

634 kN ≤ 766,39 kN

Warunki nośności dla pali wciskanych spełnione

Warunek nośności pala wyciąganego w grupie (na podstawie tabeli):

Q_r ≤ m*N_wg

Pal 3 Q_r = S₃ = 296 kN

296 kN ≤ 315,75 kN → długość pala 3: L = 14 m

Warunek nośności pojedynczego pala wciskanego

Pal 3 o długośći L = 14m Q_r = S₃ = 296 kN

296 kN ≤ 315,75 kN

Warunki nośności dla pali wyciąganych spełnione

Stan graniczny użytkowalności

23. Obliczenie osiadania pala pojedynczego (pojedynczego uwzględnieniem tarcia

negatywnego)

23.1 Osiadanie pala w gruncie nośnym (jednorodnym) zalegającym poniżej warstwy:

torfu, spowodowane obciążeniem zastępczym Q^*_n

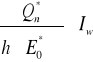
S =

gdzie:

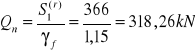
- obciążenie pala działające wzdłuż jego osi

- wartość charakterystyczna obciążenia pala tarciem

negatywnym gruntu, który osiada względem trzonu pala

Q^*_n = 318,26 + 321,78 = 640,04 kN

h = 11 - (10 - 0,9) = 1,9 m - długość pala w gruncie nośnym

E₀^*= E₀ * S_s - moduł odkształcenia gruntu, wyznaczony na podstawie

PN-81/B-03020 i przemnożony przez współczynnik

technologiczny S_s (PN-83/B-02482 tabl. 4)

E₀ dla Pr

E₀ = 85000 kPa

S_s = 1,1

E₀^* = 85000 * 1,1 = 93500 kPa

E_b^* = E₀ * S_p ­- moduł odkształcenia gruntu poniżej podstawy pala,

wyznaczony z PN-81/B-03020 i przemnożenia przez

współczynnik technologiczny S_p (wg PN-83/B-02482

tabl. 4).

S_p = 1,4

E_b^* = 85000 * 1,4 = 119000 kPa

Gdy zachodzi:

E_b^* > E₀^* to I_w = I_ok * R_b

119000 kN > 93500kN → I_w = I_ok * R_b

I_w - współczynnik wpływu osiadania

I_ok - współczynnik wpływu osiadania, przyjmowany z rys. 10

wg PN-83/B-02482, zależny od K_A i h/D

h = 1,9 m - długość pala w gruncie nośnym

D = 0,508 m - średnica pala

K_A - współczynnik sztywności równy:

E_t - moduł ściśliwości trzonu, zależny od klasy betonu

przyjęto klasę betonu B-20 o module E_t = 27,0*10⁶ kPa,

E₀^* = 93500 kPa

R_A - stosunek powierzchni przekroju poprzecznego pala do całkowitej

powierzchni przekroju poprzecznego pala

Pal Vibrex - pal pełny → R_A = 1

K_A =

I_ok = f(K_A = 288,7;
) = {z rys. 10, str. 15, wg PN-83/B-02482} = 1,25

R_b - współczynnik wpływu warstwy mniej ściśliwej w podstawie pala,

przyjmowany wg normy PN-83/B-02482 rys. 12, zależny od h/D, K_A oraz

stosunku modułów E_b^*/E_o^*.

K_A = 288,7 → R_b = 0,98

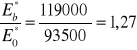
Na podstawie powyższych wartości obliczamy I_w

I_w = I_ok * R_b

I_w = 1,25 * 0,98 = 1,225

Obliczenie osiadania pala w gruncie nośnym

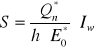
23.2 Przybliżone osiadanie pala, z warstwą nieodkształcalną w podstawie

ΔS =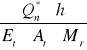

Q^*_n = 318,26 + 321,78 = 640,04 kN (patrz wyżej)

h = 11 - 1,9 = 9,1 m - długość pala powyżej gruntu nośnego

E_t = 27,0*10⁶ kPa (patrz wyżej)

A_t =
=
0,203 m² - pole powierzchni przekroju poprzecznego pala

M_r - współczynnik osiadania dla pala z warstwą

nieodkształcalną w podstawie, przyjmowany wg

normy PN-83/B-02482 rys. 13, zależny od K_A i h/D

h = 9,1 m - długość pala powyżej gruntu nośnego

D = 0,508 m - średnica pala

(patrz wyżej)

E_t = 27,0*10⁶ kPa

R_A = 1 (patrz wyżej)

Moduł odkształcenia E₀^* jako średnią ważoną z modułów poszczególnych gruntów.

Obliczenie E₀ dla torfu o M₀ = 2500 kPa, według wzoru z tabl. 3, str. 15, PN-81/B-03020.

Przyjęto υ = 0,3 (współczynnik Poissona).

kPa

Rodzaj gruntu	E0i	Ss	hi	E0i^*= E0i * Ss	E0i^*ˣ hi
		[kPa]	[-]	[m]	[kPa]	[kPa ˣ m]
Gp	28000	0,9	0,6	25200	15120
T	1857	0,9	5,4	1671,3	9025,02
Ps	99000	1,1	3,1	108900	337590
∑			9,1		361735

Tab13. Obliczenia średniej ważonej modułów E₀^* poszczególnych gruntów

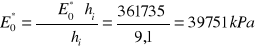
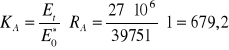
M_r = f(K_A = 679,2;
) = {z rys. 13 wg PN-83/B-02482} = 0,75

Obliczenie osiadania pala, z warstwą nieodkształcalną w podstawie

ΔS =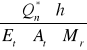

23.3 Osiadanie całkowite

Politechnika Gdańska KGGiBM

Projekt ściany oporowej Mateusz Zieliński

70

---