Ekonometria- bada związki o charakterze ilościowym występujące pomiędzy elementami zjawisk ekonomicznych za pomocą metod statystycznych i matematycznych.

Twórcami tej nauki są: R. Frisch oraz J. Tinbergen (laureaci Nagrody Nobla z ekonomii).

Ekonometrię można stosować wtedy, gdy:

• badane zjawisko ekonomiczne musi być stabilne, tj. ulegać jedynie niewielkim i powolnym zmianom,

• zjawisko musi być mierzalne, tj. jego cechy muszą być wyrażane liczbowo,

• można określić czynniki wpływające na jego zachowanie,

• dostępne są dane statystyczne opisujące zachowanie (w sensie ilościowym) badanego systemu w przeszłości.

model ekonometryczny-Podstawowe narzędzie wykorzystywanym w analizie ekonometrycznej

Model to konstrukcja teoretyczna, która podlega analizie w miejsce rzeczywistego zjawiska, pozwalając na lepsze zrozumienie jego charakteru. Jest ona zawsze znacznie uproszczonym obrazem obserwowanego zjawiska (np. model samolotu, model spirali DNA) pozwala jednak na prowadzenie eksperymentów.

Model ekonometryczny- to formalna konstrukcja, która za pomocą jednego lub kilku równań przedstawia powiązania występujące pomiędzy elementami zjawiska ekonomicznego.

Jest to model matematyczny, który został „dopasowany” do rzeczywistości za pomocą metod statystycznych.

Modele matematyczne są:

• zwięzłe,

• jednoznaczne,

• precyzyjne,

• mają logiczną strukturę,

• łatwe do wykorzystania przy użyciu komputerów.

Podział modeli ekonometrycznych

- ze względu na uwzględnienie powiązań zachodzących jednocześnie lub w kolejnych okresach czasu:

• statyczne,

• dynamiczne.

- ze względu na ilość równań:

• jednorównaniowe,

• wielorównaniowe.

- ze względu na postać funkcji opisującej charakter wpływu zmiennych X na zmienne Y:

• liniowe,

• nieliniowe.

Przykłady modeli ekonometrycznych

Liniowy (jednorównaniowy):

C = α + βY

gdzie: C - konsumpcja

Y - dochód narodowy

α, β - parametry modelu

Liniowy (wielorównaniowy):

C = α + βY

Y = C + I + G

gdzie: I - inwestycje

G - wydatki budżetowe

Nieliniowy:

I = α₀ + α₁R + α₂R² + α₃Y + α₄Y²

gdzie: R - stopa procentowa

Dynamiczny:

C_t = α₀ + α₁Y_t-1

I_t = β₀ + β₁(Y_t-1 - Y_t-2)

Y_t = C_t + I_t + G_t

gdzie: „t”, „t-1”, „t-2” oznaczają kolejne okresy czasu.

Budowa modelu ekonometrycznego

y = f(x₁ ,x₂ , ..., x_n) + u

np. model liniowy:

y = a₁x₁ + a₂x₂ + ... + a_nx_n + u

gdzie:

y - zmienna objaśniana (endogeniczna)

x₁ ,x₂ , ..., x_n - zmienne objaśniające (egzogeniczne)

a₁, a₂, ..., a_n - parametry strukturalne modelu

u - składnik losowy

Na podstawie danych statystycznych opisujących zachowanie systemu w przeszłości parametry modelu są szacowane (estymowane) za pomocą metody najmniejszych kwadratów (MNK), np.

C = 3,45 + 8,52Y + u

Oznacza to dopasowanie modelu do rzeczywistości.

Parametry strukturalne modelu wyrażają ilościowy wpływ danej zmiennej (przy której stoją) na zmienną objaśnianą.

Składnik losowy uwzględnia:

• wpływ innych zmiennych niż te, które są już w modelu,

• różnice między modelem a rzeczywistością,

• błędy pomiaru zmiennych,

• działanie czynników losowych.

Etapy budowy modelu ekonometrycznego

1. specyfikacja modelu - określenie zmiennych objaśnianych i objaśniających, postaci analitycznej modelu oraz źródeł danych statystycznych,

2. estymacja parametrów modelu - na podstawie zgromadzonych danych za pomocą MNK,

3. weryfikacja modelu - określenie, czy wyniki są zgodne z teorią ekonomiczną oraz statystyką,

4. wykorzystanie modelu - do symulacji i tworzenia prognoz.

Specyfikacja modelu

I. Dobór zmiennych objaśniających

Zmienne muszą:

• mieć wysoką zmienność, tj. współczynnik zmienności

w przeciwnym wypadku są to zmienne quasi-stałe

• być silnie skorelowane ze zmienną objaśnianą,

• nie być skorelowane ze sobą.

Zmienne spełniające oba warunki można wybrać stosując metodę formalną, tzw. metodę Hellwiga.

Obliczamy macierz współczynników korelacji pomiędzy zmiennymi objaśniającymi:

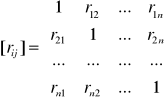
oraz wektor:

współczynników korelacji zmiennych objaśniających ze zmienną objaśnianą.

Rozważa się wszystkie możliwe kombinacje zmiennych objaśniających, których jest:

Dla każdej kombinacji oblicza się indywidualny wskaźnik pojemności informacyjnej:

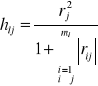
gdzie l = 1 ,..., L,

j = 1 ,..., m_l,

m_l - liczba zmiennych w kombinacji

Integralne wskaźniki pojemności całych kombinacji:

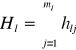
Wybierana jest ta kombinacja zmiennych, dla której H jest największe:

Przykład:

Zmienne x1, x2, x3, x4.

Macierz korelacji i wektor:

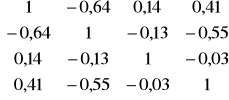
Kombinacje zmiennych:

1:{x1} 5:{x1,x2} 10:{x3,x4} 15:{x1,x2,x3,x4}

2:{x2} 6:{x1,x3} 11:{x1,x2,x3}

3:{x3} 7:{x1,x4} 12:{x1,x2,x4}

4:{x4} 8:{x2,x3} 13:{x1,x3,x4}

9:{x2,x4} 14:{x2,x3,x4}

Dla np. kombinacji nr 5 liczymy:

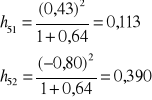
oraz:

Okazuje się, że maksymalna wartość pojemności występuje dla kombinacji nr 9, tj. {x2,x4} i wynosi 0,668.

Problem: zmienne jakościowe, np. branża, wykształcenie, posiadanie bazy transportowej itp.

Wtedy zamieniamy te zmienne na zero-jedynkowe i wstawiamy je do modelu. Na przykład:

• zmienna „wykształcenie pracownika” (podstawowe, średnie, wyższe)

Zamieniamy ją na 2 zmienne zero-jedynkowe:

z1=0 gdy podstawowe,

z1=1 gdy średnie lub wyższe,

z2=0 gdy podstawowe lub średnie,

z2=1 gdy wyższe.

Sprawia trudności jednak interpretacja parametrów przy takich zmiennych.

II. Wybór postaci analitycznej modelu

Kiedy jest jedna zmienna objaśniająca - wykres rozrzutu.

W innym wypadku - teoria ekonomii, literatura, praktyka i doświadczenie.

Estymacja parametrów modelu ekonometrycznego

Parametry modelu

Y = aX + b

można oszacować na podstawie danych statystycznych opisujących zachowanie modelowanego zjawiska w przeszłości.

Do tego celu stosowana jest metoda najmniejszych kwadratów polegająca na minimalizacji

(Y-aX)^T(Y-aX) →min

Rozwiązaniem jest macierz parametrów:

a = (X^TX)^-1X^TY

Opisują one siłę oraz kierunek wpływu zmiennych objaśniających (X) na zmienną objaśnianą (Y).

Weryfikacja modelu

Po oszacowaniu parametrów należy sprawdzić, czy model jest dobry, tj.

• jest zgodny z rzeczywistością,

• jest precyzyjny,

• zmienne objaśniające (X) istotnie wpływają na zmienną objaśnianą (Y).

Do oceny dopasowania modelu do rzeczywistych danych wykorzystuje się:

• wariancję resztową:

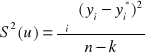
lub w zapisie macierzowym:

gdzie „reszta” oznacza różnicę między wartością empiryczną y_i a teoretyczną y_i^*.

• współczynnik zbieżności:

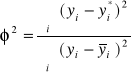
• współczynnik determinacji:

R² = 1 - φ²

Współczynnik determinacji przyjmuje wartości z przedziału [0,1] i informuje jaka część zmian zmiennej objaśnianej Y została wyjaśniona przez model.

Na przykład R² = 0,7 oznacza, iż model w 70% wyjaśnia zmiany zmiennej Y.

Istotność parametrów

Wektor parametrów modelu:

a = (X^TX)^-1X^TY

ma macierz wariancji i kowariancji równą:

D²(a) = S²(u)(X^TX)^-1

Na głównej przekątnej znajdują się wariancje parametrów modelu:

D²(a_i)

Wtedy błąd szacunku parametru a_i jest równy:

D(a_i)

Istotność statystyczną parametrów mierzymy za pomocą sprawdzianu:

gdzie „t” ma rozkład Studenta o n-k stopniach swobody.

Z tablic rozkładu t-Studenta znajdujemy wartość krytyczną t_α dla zadanego poziomu istotności α.

Zwykle jest to α=0,05.

Jeżeli zachodzi nierówność:

to oznacza, że zmienna x_i (przy której stoi parametr a_i) istotnie wpływa na zmienną objaśnianą (y).

W przeciwnym wypadku zmienna ta jest zbędna i należy ją usunąć z modelu.

Dane

y - cena akcji (zł)

x₁ - obroty (mln zł)

x₂ - liczba zatrudnionych (w setkach osób)

y	x1	x2
10	0,6	10
9	0,5	8
11	0,9	8
13	1,1	9
12	1,0	8
15	1,2	7
14	0,9	5
16	1,3	4
17	1,5	4

Należy oszacować parametry strukturalne modelu ekonometrycznego:

y = a₀ + a₁x₁ + a₂x₂ + u

Za pomocą metody najmniejszych kwadratów wektor parametrów liczymy jako:

a = (X^TX)^-1X^TY

Można zastosować skrócone obliczenia:

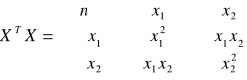
oraz:

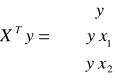
Zatem potrzebne są obliczenia pomocnicze:

y	x1	x2	x1 x2	x^21	x^22	y x1	y x2	y^2
10	0,6	10	6,0	0,36	100	6,0	100	100
9	0,5	8	4,0	0,25	64	4,5	72	81
11	0,9	8	7,2	0,81	64	9,9	88	121
13	1,1	9	9,9	1,21	81	14,3	117	169
12	1,0	8	8,0	1,00	64	12,0	96	144
15	1,2	7	8,4	1,44	49	18,0	105	225
14	0,9	5	4,5	0,81	25	12,6	70	196
16	1,3	4	5,2	1,69	16	20,8	64	256
17	1,5	4	6,0	2,25	16	25,5	68	289
117	9,0	63	59,2	9,82	479	123,6	780	1581

Macierze mają postać:

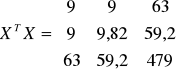
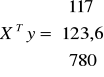
Aby odwrócić macierz X^TX należy obliczyć wyznacznik, który wynosi 150,48 oraz zastosować metodę Sarriusa.

W rezultacie macierz odwrotna ma postać:

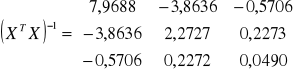
Po dokonaniu obliczeń wektor parametrów "a" ma postać:

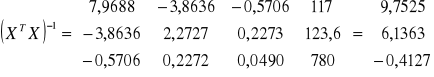
Model ekonometryczny ma więc postać:

y = 9,752 + 6,136 x₁ - 0,431 x₂

Następnie przechodzimy do weryfikacji modelu. Liczymy wariancję resztową:

Czyli:

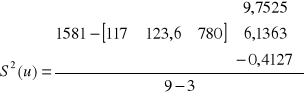
Odchylenie standardowe reszt:

S(u)=0,756

Macierz wariancji i kowariancji ocen parametrów:

D²(a) = S²(u)(X^TX)^-1

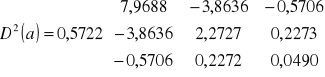
Pierwiastki elementów na przekątnej to błędy szacunku parametrów a_i:

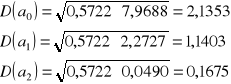
Istotność statystyczną parametrów mierzymy za pomocą:

czyli:

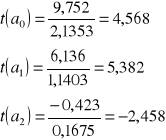
Jeżeli zachodzi nierówność:

to oznacza, że zmienna x_i (przy której stoi parametr a_i) istotnie wpływa na zmienną objaśnianą (y).

Z tablic rozkładu Studenta dla α=0,05 i 9-3=6 stopni swobody

t_α=2,447

Ponieważ powyższa nierówność zachodzi, to wszystkie parametry modelu są statystycznie istotne.

Jakość modelu oceniamy licząc współczynnik zbieżności:

Stąd:

czyli 5,72%.

Współczynnik determinacji wynosi:

R² = 1 - φ²

czyli:

R² = 1 - 0,0572 = 0,9428

czyli 94,28%, co oznacza znakomitą jakość modelu (dopasowanie do danych empirycznych).

Analiza reszt modelu ekonometrycznego

Poprawnie skonstruowany model ekonometryczny powinien charakteryzować się pewnymi pożądanymi właściwościami reszt. Należą do nich:

• losowość reszt,

• symetria rozkładu reszt,

• brak autokorelacji reszt (gdy model jest dynamiczny, tj. uwzględnia zmiany w czasie)

Losowość badamy na przykład za pomocą tzw. testu serii.

Polega on na tym, że wyznaczonym resztom przypisujemy symbol "a", gdy u_i>0 oraz "b", gdy u_i<0. Można w nim zaobserwować serie, tj. ciągi symboli "a" i "b". Ich liczbę określamy jako "k". Następnie z tablic odczytujemy wartość graniczną (krytyczną) "K". Jeżeli jest spełniony warunek:

k>K

to reszty mają charakter losowy.

Przykład

Dla modelu:

y = 9,752 + 6,136 x₁ - 0,431 x₂

obliczono reszty:

y	y^*	ui
10	9,33	0,67
9	9,54	-0,54
11	12,0	-1,0
13	12,81	0,19
12	12,61	-0,61
15	14,25	0,75
14	13,23	0,77
16	16,09	-0,09
17	17,32	-0,32

Uzyskujemy ciąg symboli:

abbabaabb

Liczba serii wynosi k=6. Z tablic wartość krytyczną (dla poziomu istotności α=0,05) odczytujemy jako K=2.

Ponieważ k>K, to uznajemy, że reszty mają charakter losowy.

Symetrię reszt badamy za pomocą testu:

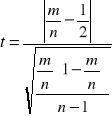
gdzie:

m - liczba reszt dodatnich (u_i>0),

n - liczba obserwacji

Dla n≤30 statystka ta ma rozkład Studenta, a gdy n>30 - rozkład normalny.

Z tablic rozkładu Studenta dla α=0,05 i n-1 stopni swobody znajdujemy wartość krytyczną t_α. Jeżeli spełniona jest nierówność:

t<t_α

to oznacza symetrię reszt.

Przykład

Dla danych podanych wyżej mamy: n=9, m=4. Wtedy wartość testu wynosi:

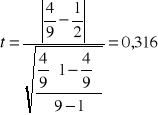
Odczytana z tablic rozkładu Studenta wartość t_α = 2,306.

Zatem 0,316 < 2,306, czyli reszty modelu są symetryczne.

Autokorelacja reszt

oznacza liniową zależność pomiędzy resztami modelu odległymi od siebie o "k" okresów. Dotyczy to modeli dynamicznych.

Jej występowanie oznacza, że:

• pominięto w modelu jedną z istotnych zmiennych objaśniających,

• lub przyjęto niewłaściwą postać modelu.

Liczy się ją jako współczynnik korelacji liniowej Pearsona miedzy resztami. Na przykład dla k=1 mamy:

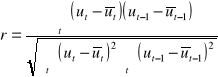
Aby sprawdzić, czy reszty modelu są skorelowane, należy obliczyć wartość testu:

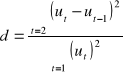
Z tablic Durbina-Watsona odczytuje się wartości graniczne d_D oraz d_G i jeżeli spełniony jest warunek:

d<d_D

to oznacza, że autokorelacja nie występuje. Zaś gdy:

d>d_G

to zjawisko to występuje.

Tak postępujemy, gdy d<2 (autokorelacja dodatnia).

W przeciwnym wypadku (autokorelacja ujemna) liczymy d'=4-d.

Przykład

Dla k=1 obliczono reszty:

ut	ut-1	ut - ut-1	(ut - ut-1)^2	ut^2
0,67				0,4489
-0,54	0,67	-1,21	1,4641	0,2916
-1,0	-0,54	-0,46	0,2116	1,0000
0,19	-1,0	1,19	1,4161	0,0361
-0,61	0,19	-0,8	0,6400	0,3721
0,75	-0,61	1,36	1,8496	0,5625
0,77	0,75	0,02	0,0004	0,5929
-0,09	0,77	-0,86	0,7396	0,0081
-0,32	-0,09	-0,23	0,0529	0,1024
			6,3743	3,4146

Na tej podstawie obliczono:

Ponieważ d<2, to d=1,867

Dla poziomu istotności α=0,05 w tablicach znaleziono:

d_D=0,80 oraz d_G=1,54

Ponieważ d > d_G, oznacza to, że występuje autokorelacja reszt modelu odległych o k=1.

Elastyczność

Jest jedną z metod wnioskowania na podstawie modelu ekonometrycznego y = f(x₁, x₂, ..., x_k).

Mierzy wielkość względnej zmiany zmiennej objaśnianej (y) pod wpływem określonych, względnych zmian jednej ze zmiennych objaśniających (x_i).

Najczęściej chodzi o pytania typu: "o ile % zmieni się y, jeżeli x_i wzrośnie o 5% ?".

Wyróżniamy trzy rodzaje elastyczności:

• elastyczność klasyczna,

• elastyczność różnicowa,

• elastyczność całkowita.

Klasyczna definicja elastyczności

Elastycznością zmiennej y względem zmiennej x_i nazywamy wyrażenie:

czyli pochodną cząstkową funkcji f(x₁, x₂, ..., x_k) względem zmiennej x_i.

Efekt względnych zmian wyraża zależność:

Elastyczność klasyczna ma zastosowanie gdy:

• zmiany zmiennej objaśniającej x_i są bliskie zero:

Δ x_i → 0

• zmiany zmiennej x_i nie wywołują zmian innych zmiennych.

Przykład

Mając model kosztów całkowitych (mln zł):

y = 2 x + 20

gdzie "x" oznacza wielkość produkcji (tys. sztuk), należy obliczyć klasyczną elastyczność dla x=10 tys. sztuk.

Elastyczność określa wzór:

Podstawiając x=10, otrzymujemy:

Oznacza to, że przy produkcji wynoszącej 10 tys. sztuk, jej wzrost o 1% spowoduje wzrost kosztów całkowitych o 0,5%.

Elastyczność różnicowa

Założenie o tym, że zmiany zmiennej objaśniającej x_i są bliskie zero (Δ x_i → 0) jest krępujące, gdyż nie pozwala uwzględnić dużych przyrostów zmiennych objaśniających.

Wtedy lepiej wykorzystać elastyczność różnicową:

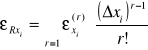
gdzie elastyczność rzędu "r" wyznacza się z wzoru:

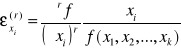
Zwykle w szeregu wystarczy uwzględnić 3 pierwsze wyrazy, co daje wzór:

W modelach liniowych elastyczność różnicowa jest równa elastyczności klasycznej.

Przykład

Mając model produkcji (y):

gdzie x₁ to zatrudnienie, a x₂ - kapitał, obliczymy względny przyrost produkcji, gdy zatrudnienie wzrośnie o 40%.

Elastyczności rzędu pierwszego, drugiego i trzeciego:

Elastyczność różnicowa:

Podstawiając:

otrzymujemy:

Czyli wzrost zatrudnienia o 40% spowoduje wzrost produkcji o 46%.

Elastyczność całkowita

Jest stosowana wtedy, gdy zmiana zmiennej objaśniającej x_i jest bliska zero (Δ x_i → 0), ale pociąga ona za sobą zmiany innych (m) zmiennych objaśniających w modelu.

Wtedy poza wpływem zmiennej x_i na zmiany y należy także uwzględniać efekty pośrednie.

Miara ma postać:

gdzie:

to efekt bezpośredni,

- elastyczność x_j względem y,

- elastyczność x_j względem x_i.

Modele produkcji

• Cobba-Douglasa

wyraża zależność między wielkością produkcji (Y) a różnymi rodzajami nakładów (pracy, środków itp.) oznaczanych jako X₁, X₂, ..., X_k:

w najprostszej postaci jest to model dwuczynnikowy:

gdzie: Y - produkcja,

K - kapitał (wartość brutto majątku trwałego),

L - praca (liczba zatrudnionych),

a₀, a₁, a₂ - parametry,

u - składnik losowy.

Czasami przyjmuje się także założenie o stałej wydajności produkcji, tj. a₁+ a₂=1.

Jest to funkcja nieliniowa i aby oszacować jej parametry za pomocą metody najmniejszych kwadratów (MNK) należy ją sprowadzić do postaci liniowej przez logarytmowanie:

Daje to model liniowy:

Przykład:

Dla pewnych danych uzyskano model:

gdzie parametry mają następujące znaczenie:

0,45 - elastyczność produkcji względem kapitału, tj. jeżeli kapitał wzrośnie o 1%, to produkcja wzrośnie przeciętnie o 0,45% (jeżeli liczba zatrudnionych się nie zmieni),

0,51 - elastyczność produkcji względem pracy, tj. jeżeli liczba zatrudnionych wzrośnie o 1%, to produkcja wzrośnie średnio o 0,51%

Jeżeli ustalimy produkcję na pewnym poziomie (Y₀), to można oszacować wielkość kapitału i pracy:

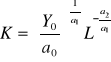
oraz:

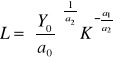
np. jeżeli zatrudniono 707 osób, a wartość produkcji wynosi 2,05 mln zł, to wartość kapitału powinna wynieść:

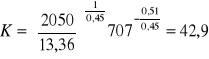
42,9 mln złotych (przy nie zmienionym zatrudnieniu).

Można także określić krańcowe stopy substytucji kapitału, np. jeżeli wartość kapitału (majątku trwałego) spadnie o 5 mln zł, to utrzymując produkcję na poziomie 2,05 mln zł należy zwiększyć zatrudnienie o:

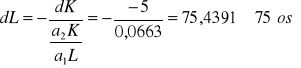
Ponieważ

a₁+ a₂=0,96 to rozpatrywany proces produkcji charakteryzuje się malejącymi przychodami względem skali produkcji, tj. przyrost czynników produkcji daje mniej niż proporcjonalny przyrost produkcji.

• CES (Constant Elasticity of Substitution)

Funkcja o stałej elastyczności substytucji. Jest uogólnieniem modelu Cobba-Douglasa, chociaż trudno szacować jej parametry:

gdzie: a₁+...+ a_k = 1.

W najprostszej postaci jest to model dwuczynnikowy:

gdzie:

oznaczenia są takie same jak poprzednio,

a₁, a₂, b, c - parametry, przy czym:

Jest to model nieliniowy i nie istnieje transformacja przekształcająca go na liniowy.

Przykład:

Dla pewnych danych uzyskano model:

Można obliczyć o ile wzrośnie produkcja, jeżeli zatrudnienie wzrośnie o 2%, a wartość środków trwałych nie ulegnie zmianie.

Wtedy:

zatem, gdy w bieżącym okresie produkcja wynosi 87 mln zł, a zatrudnienie 70 osób, to:

więc:

czyli produkcja wzrośnie o 0,7064%.

Można obliczyć o ile wzrośnie produkcja, jeżeli oba czynniki produkcji wzrosną jednocześnie o 5%.

Wtedy:

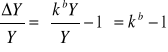
gdzie k oznacza krotność wzrostu („k” razy). Czyli:

czyli produkcja wzrośnie o 4,463%.

Model wydajności pracy

Zależność wydajności pracy od wieku pracownika jest wyrażana za pomocą funkcji:

gdzie: W - wydajność,

T - wiek,

u - składnik losowy.

Jest to funkcja nieliniowa i należy ją sprowadzić do postaci liniowej przez logarytmowanie:

Daje to model liniowy:

Przykład:

Dla pewnych danych uzyskano model:

Można obliczyć optymalny wiek pracownika (tj. wiek, w którym osiąga maksymalną wydajność). Oznacza to, że:

czyli:

a ponieważ zawsze W > 0, więc T=30 lat.

Jego maksymalna wydajność jest wtedy równa:

wykonania normy.

Model kosztów

Może mieć postać wielomianową:

gdzie: K - koszt,

Q - wielkość produkcji.

Przykład:

Koszt wydobycia węgla w pewnej kopalni ze względu na miesięczne wydobycie jest opisany funkcją:

Można wtedy np. obliczyć koszt całkowity wydobycia 5 tys. ton węgla:

Wynosi on 709 tys. zł.

Można obliczyć optymalną z punktu widzenia kosztów jednostkowych wielkość wydobycia. Funkcja kosztów jednostkowych ma postać:

Osiąga ona minimum gdy:

czyli dla Q = 3,8639 tys. ton.

Ten minimalny koszt wynosi:

czyli 139,4 tys. zł

Model dochodów

Do opisu rozkładu dochodów ludności najczęściej stosuje się model Pareto:

gdzie:

Y - liczba osób o dochodach większych lub równych od x,

x - poziom dochodów,

a, b - parametry.

Jest to funkcja nieliniowa i należy ją sprowadzić do postaci liniowej przez logarytmowanie:

Przykład:

Dla pracowników sfery handlu w roku 1992 zbudowano model dochodów:

Modele popytu

wyrażają zależność poziomu popytu (Y) od grupy czynników ekonomicznych i pozaekonomicznych (X), np. cena, dochód itd. Może to być model:

• potęgowy:

• hiperboliczny:

• Tornquista:

1) dla dóbr pierwszej potrzeby:

2) dla dóbr wyższego rzędu:

3) dla dóbr luksusowych:

Przy czym: Y - wydatki na dane dobro lub grupę dóbr,

X - dochody gospodarstw.

Przykład:

W pewnej grupie osób wydatki na kulturę opisano jako funkcję Tornquista drugiego rodzaju dochodów. Po estymacji uzyskano model:

Parametr a₁ oznacza poziom, do którego wydatki rosną,

a₃ - poziom dochodów, przy którym pojawiają się wydatki na analizowane dobro.

Czyli wydatki na kulturę pojawiają się jeżeli miesięczny dochód na osobę osiągnie poziom 143,81 zł i będą rosły w miarę wzrostu dochodów aż do poziomu 167,57 zł.

Literatura:

Kukuła „Elementy ekonometrii w przykładach i zadaniach”

Kukuła „Badania operacyjne w zadaniach i przykładach”

Pawłowski „Ekonometria” (wszystkie pozycje o tym tytule)

Chow (1995)

„Ekonometria jest nauką i sztuką stosowania metod stystycznych do mierzenia relacji ekonomicznych”.

Pawłowski (1978)

„Ekonometria jest nauką o metodach badania ilościowych prawidłowości występujących w zjawiskach ekonomicznych za pomocą odpowiednio wyspecjalizowanego aparatu matematyczno - statystycznego” .

Metody ekonometryczne

Hellwig (1973)

„Metody ekonometryczne sa to więc przeważnie metody statystyczne (rzadziej matematyczne), przy czym nazwą ekonometrycznych zawdzięczaja dziedzinie zastosowań”.

Metody ekonometryczne są możliwe, kiedy spełnione są 4 warunki:

1. analizowana prawidłowość ekonomiczna ulega nieznacznym zmianom w czasie bądź może być stała.

2. zjawisko ekonomiczne i pozaekonomiczne musi być mierzalne.

3. czynniki oddziałujące na badane środowisko dzielimy na grupy:

• czynniki dominujące

• czynniki przypadkowe

4. dostępne muszą być dane statystyczne analizowanych czynników.

Rodzaje danych:

1. szeregi czasowe wartości zmiennych w postaci zasobów( na dany okres czasu) i strumieni (np. za cały miesiąc).

2. dane przekrojowe (rozważamy zjawisko w jednym momencie dla różnych jednostek.

Zadania ekonometrii możemy podzielić na:

1. opisowo - analityczne - wykorzystywane do analizy relacji zachodzących pomiędzy zmiennymi

2. prognostyczne - wyznaczanie i obliczanie prognoz.

Modele ekonometryczne

Narzędziem ekonometrycznym służącym do analizy zależności zachodzacych między różnymi zjawiskami jest model ekonometryczny.

„Model ekonometryczny jest to konstrukcja formalna, która za pomocą jednego równania lub układu równań przedstawia zasadnicze powiązania wystepujące pomiędzy rozpatrywanymi zjawiskami ekonomicznymi”.

Postać modelu

y = f (x,ξ)

Zmienna endogeniczna y jest to zmienna wyjaśniona przez model (jest ona przedmiotem analizy).

Zmienna endogeniczna objaśniana jest przedmiotem analizy w pojedynczym równaniu (y).

Zmienna objaśniająca x to zmienne, które opisują kształtowanie się zmiennej endogenicznej (pojedyncze równanie).

Zmienne egzogeniczne to takie zmienne objaśniające, które występują w modelu w celu opisania kształtowania się zmiennej y , ale same nie są przedmiotem analizy.

Symbol ξ jest to składnik losowy.

y = f (x , ξ)

część dominująca część przypadkowa

Symbol f( ) oznacza określoną postać analityczną funkcji zmiennych objaśniających.

W modelu występują dwa rodzaje parametrów:

• parametry strukturalne modelu,

• parametry struktury stochastycznej modelu, czyli parametry rozkładu ξ modelu.

Wszystko co jest związane ze składnikiem losowym jest stochastyczne.

Przykładem modelu ekonometrycznego może być model konsumpcji:

K₁ = β₀ + β₁D_t +ξ_t

t - szereg czasowy

i - szereg przekrojowy

D_t - dochód

ξ_{t -} przypadkowy

Klasyfikacja modeli ekonometrycznych.

Klasyfikacja modeli ekonometrycznych dokonuje się na podstawie następujących kryteriów:

• 
  cel badania - opisowe ekonometria

- optymalizujące programowanie liniowe (operacyjne)

• występowanie składnika losowego:

• deternistyczne (składnik losowy nie występuje)

• stochastyczne (składnik losowy występuje)

• postać funkcji analitycznej:

• liniowe

• nieliniowe

• sprowadzalne do liniowych

• niesprowadzalne do liniowych

• liczba rozpatrywanych zależności:

• jednorównaniowych

• wielorównaniowych

• dynamiczność zależności:

• statyczne (to modele, w których rozważane zmienne pochodzą z tego samego określonego czasu i opisują zależności w tym samym okresie czasu)

• dynamiczne (modele, w których występują zmienne endogeniczne opóźnione w czasie y_t-p, p=1,.....,m lub zmienne egzogeniczne opóźniane w czasie X_t-q q=1,...,n lub zmienna czasowa t.

• zakres badania:

• mikroekonomiczne

• makroekonomiczne

• charakter powiązań między zmiennymi endogenicznymi (charakter dotyczy modeli wielorównaniowych):

• prosty - jest to model w którym nie ma powiązań pomiędzy zmiennymi endogenicznymi

• rekurencyjny - powiązania pomiędzy zmiennymi endogenicznymi są jednokierunkowe.

• o równaniach współzależnych (powiązania maja charakter sprężeń zwrotnych).

• charakter poznawczy:

• przyczynowo - skutkowy - możemy bezpośrednio określić, które zmienne są przyczyną, a które skutkiem

• symptomatyczny - nie możemy bezpośrednio określić skutku. Związek pomiędzy zmienną egzogeniczną i endogeniczną jest określany na podstawie silnej korelacji

• tendencji rozwojowej - opisują przebieg zjawiska w czasie.

Etapy budowy modelu ekonometrycznego

sprecyzowanie zakresu

badania

określenie zmiennych

endogenicznych

dobór zmiennych

objaśniających

zebranie danych

statystycznych

wybór postaci

analitycznej modelu

estymacja

parametrów modelu

weryfikacja modelu

wykorzystanie

modelu

Zasady interpretacji parametrów w modelach statystycznych.

1. Model liniowy

y_t = β₀ + β₁x_t1 + β_2t2 + .... + β_kx_tk + ξ_t

t = 1,.....,T

czyli

y_t = β₀ +
β_tx_ti + ξ_t

wektor obserwacji na zmiennej endogenicznej oraz macierz obserwacji na zmiennych egzogenicznych przyjmują postacie odpowiednio:

y₁ 1 x₁₁ x₁₂ ... x_1k

Y = y₂ , x = 1 x₂₁ x₂₂ ... x_2k

: : : : : :

y_T 1 x_T1 x_T2 ... x_TK

Interpretacja parametru βi

jeżeli zmienna x_t wzrośnie o jednostkę, a pozostałe zmienne objaśniające nie ulegną zmianie to zmienna endogeniczna zmieni się średnio o β_i jednostek.

k - liczba zmiennych objaśniających równania

β - parametr strukturalny modelu

k+1 - liczba parametrów strukturalnych

T - liczba obserwacji

Liczba stopni swobody:

T - (k+1) = T - k - 1

2. Model potęgowy

y_t = β₀ x^β
x^β
* ... * x^β
ξ_t t= 1, ...,T

lub

ln y_t = ln β₀ + β₁ ln x_t1 +
β₂ ln x_t2 + ... β_k ln x_tk + ln ξ_t

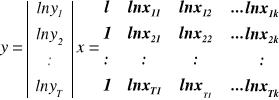
Interpretacja parametru β_i:

Jeżeli zmienna x_i wzrośnie o 1% , a pozostałe zmienne objaśniające nie ulegną zmianie to zmienna endogeniczna zmieni się średnio o β_i%.

3. Model wykładniczy

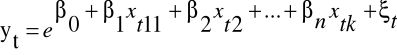
t = 1, ...,T

w postaci liniowej

lny_t = β₀ + β₁x_t1 + β₂x_t2 + ....+ β_kx_tk + ξ_t

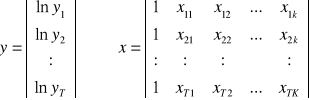
interpretacja parametru β_i:

jeżeli zmienna x_i wzrośnie o jednostkę, a pozostałe zmienne nie ulegną zmianie, to zmienna endogeniczna zmieni się średnio o (e ^βi - 1) * 100% czyli w przybliżeniu o β_i * 100%.

Metoda Najmniejszych Kwadratów (MNK).

Metoda ta wykorzystywana jest do szacowania parametrów modeli liniowych oraz modeli nieliniowych, które można sprowadzić do postaci liniowej.

Niech będzie dany model:

gdzie:

y - zmienna objaśniana

x - zmienna objaśniająca

β - parametry strukturalne

ξ - składnik losowy

t - subskrypt numerujący kolejne obserwacje (t = 1,2,....,T)

k - liczba zmiennych objaśniających

Powody uwzględniania składnika losowego:

• indeterminizm (nieokreśloność) - np. konsument w warunkach wyboru za każdym razem przy tych samych warunkach może podjąć nieco inną decyzję;

• błędy obserwacji wynikające np. z nierzetelności;

• wady w konstrukcji modelu wynikające np. z niewłaściwej konstrukcji dynamicznej modelu.

Założenia modelu regresji liniowej:

1. Postać funkcjonalna modelu jest liniowa.

2. 
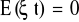
   , czyli wartość oczekiwana składnika losowego jest równa zero, nie występują wahania przypadkowe, składnik losowy nie zadziała.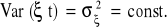

3. 
   , czyli wariancja składnika losowego jest stała w czasie; jeżeli wystąpią już wahania w czasie to zawsze o tą samą wartość.

ξ t - jest homoskedastyczny - posiada stałą wariancję w czasie

4. 
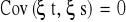
   , jeśli t ≠ s, założenie o braku autokorelacji składnika losowego.

Autokorelacja - jest to przenoszenie oddziaływania składnika losowego z okresu t na składnik losowy z okresu s.

5. 
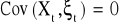
   , czyli zmienne objaśniające są zmiennymi nielosowymi.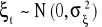

6. 
   , czyli składnik losowy ma rozkład normalny o wartości oczekiwanej równej zero i wariancji stałej w czasie, wynika to z założenia 2 i 3.

Powyższe założenia są to założenia stochastyczne, czyli dotyczące składnika losowego.

Zapis macierzy modelu:

Założenia numeryczne MNK:

1. rz (X) = k + 1, czyli rząd macierzy X równa się liczbie parametrów strukturalnych.

2. k + 1 < T, czyli liczba szacowanych parametrów musi być mniejsza od liczby obserwacji.

Rząd macierzy - jest to liczba liniowo niezależnych kolumn.

- reszta jest oceną nieznanej rzeczywistej wartości składnika losowego ξ wyznaczoną na podstawie oszacowanego modelu.

Ideą KMNK (Klasyczna Metoda Najmniejszych Kwadratów) jest minimalizacja sumy kwadratów reszty.

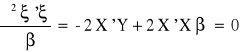
Warunek konieczny istnienia funkcji ekstremum:

Druga pochodna jest określona nieujemnie:

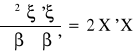
a zatem postać estymatora uzyskanego klasyczną metodą najmniejszych kwadratów jest następująca:

Współliniowość zmiennych a założenia numeryczne.

Jeżeli nie będą spełnione założenia numeryczne wówczas występuje współliniowość zmiennych objaśniających.

Współliniowość zmiennych - polega na tym, że szeregi reprezentujące zmienne objaśniające są nadmiernie skorelowane.

Konsekwencje występowania współliniowości:

1. W przypadku współliniowości dokładnej brak możliwości oszacowania parametrów modelu metodą MNK.

r (x) = k + 1

Jeżeli występuje zależność między zmiennymi strukturalnymi to:

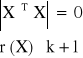
nie możemy zastosować tego wzoru:

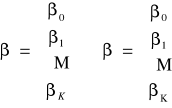
2. W przypadku wysokiej korelacji oceny wariancji estymatorów MNK są bardzo duże.

Wyznacznik macierzy zmierza do zera, ale nie może go osiągnąć.

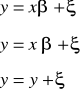
Reszta obliczana jest w sposób następujący:

wartość oszacowana

wartość rzeczywista

Własności estymatora MNK.

Estymator jest BLUE (the Best Linear Unbiased Estimator), czyli najlepszy liniowy nieobciążony estymator.

Własności estymatora MNK:

• nieobciążony - obliczona wartość parametrów strukturalnych jest równa ich wartości rzeczywistej;

• zgodny - dla dowolnie wybranej grupy (nieskończenie wiele obserwacji) zawsze otrzymamy tę samą wartość parametru β;

• najefektywniejszy - estymator ma najmniejszą wariancję spośród wszystkich możliwych do wyznaczenia estymatorów.

Średnie błędy szacunku parametrów strukturalnych obliczamy na podstawie:

Losowe błędy estymacji mają wariancje i kowariancje, które są elementami macierzy wariancji i kowariancji błędów ocen parametrów strukturalnych, oznaczaną przez:

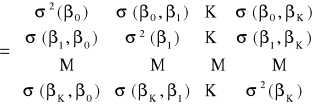
Błędy estymacji parametrów są liniowymi funkcjami składników zakłócających, czyli:

otrzymuje się:

Średnie błędy ocen parametrów oblicza się jako pierwiastki kwadratowe z kolejnych elementów wariancji i kowariancji błędów estymacji parametrów.

Weryfikacja modelu ekonometrycznego.

Polega na sprawdzeniu czy przyjęte założenia dotyczące modelu są spełnione w świetle uzyskanych wyników.

Etapy weryfikacji:

1. Weryfikacja jakościowa - dotycząca założeń ekonomicznych, sprawdzamy czy wyznaczone parametry mają sens ekonomiczny.

2. Weryfikacja ilościowa - weryfikacja hipotez statystycznych (wariancja w czasie, autokorelacja, rozkład normalny).

Weryfikacja ilościowa obejmuje:

• badanie normalności rozkładu składnika losowego;

• badanie homoskedastyczności rozkładu składnika losowego;

• badanie autokorelacji składnika losowego;

• badanie istotności zmiennych objaśniających;

• analizę syntetycznych miar dopasowania - służą do sprawdzenia czy model dobrze odzwierciedla kształtowanie się zmiennej endogenicznej.

1. Wariancja resztowa:

Ocena oszacowania:

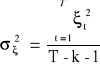
Reszta:

Określa średnie kwadratowe odchylenie wartości teoretycznych od rzeczywistych zmiennych endogenicznych.

2. Odchylenie standardowe reszt (średni błąd resztowy):

Określa o ile jednostek średnio rzecz biorąc (±) wartości rzeczywiste zmiennej endogenicznej odchylają się od wartości teoretycznych wyznaczonych na podstawie modelu.

3. Współczynnik zmienności losowej:

V = (0%, 10%)

Określa procentowy udział średniego błędu resztowego w średniej wartości zmiennej endogenicznej.

Zapis modelu liniowego:

gdzie:

y_t - zmienna rzeczywista

ŷ_t - zmienna teoretyczna, model

ξ_t - reszta

oraz własności:

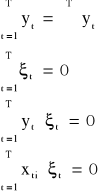
1. suma wartości y = suma wartości ŷ

2. suma reszt = 0

3. iloczyn wartości y i reszt = 0

4. dla i = 1, 2, 3, ... , k

Pozwalają na zapis równości:

Zmienność rzeczywista = zmienność teoretyczna + zmienność reszt

Ogólna suma kwadratów :

OSK = WSK + RSK

RSK - resztowa suma kwadratów

OSK = WSK + RSK

Dzieląc obustronnie przez zmienność rzeczywistą otrzymamy:

4. Współczynnik determinacji:

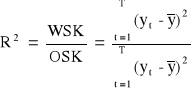
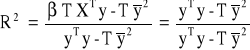
Określa jaka część całkowitej zmienności zmiennej endogenicznej została wyjaśniona przez model empiryczny.

Wadą R² jest to, że można jej wartość sztucznie zawyżać dodając do modelu zmiennych objaśniających i/lub obserwacji.

Interpretacja R² ma sens tylko wtedy, gdy w modelu występuje wyraz wolny. Jeżeli nie występuje to R² może być ujemny.

5. Współczynnik zbieżności:

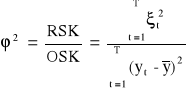
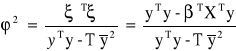
Informuje jaka wartość rzeczywistej zmienności zmiennej endogenicznej nie została wyjaśniona przez model.

Można zauważyć, że:

w celu usunięcia wad liczymy:

6. Skorygowany współczynnik zbieżności:

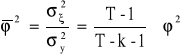
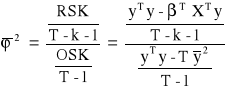
7. Skorygowany współczynnik determinacji:

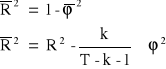
Jeżeli w modelu występują nieistotne zmienne objaśniające oraz zbyt dużo obserwacji wówczas mamy do czynienia ze zjawiskiem pozornego wyjaśnienia, które występuje wtedy, gdy różnica pomiędzy
jest duża.

Można zauważyć, że:

8. Współczynnik korelacji wielorakiej:

- siła związku między wartością rzeczywistą, a oszacowaną.

Współczynnik korelacji wielorakiej jest równy współczynnikowi korelacji liniowej Pearsona.

Indywidualna istotność parametrów strukturalnych.

Niech dany będzie model:

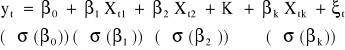
Jeżeli składniki losowe ξ_t mają rozkłady normalne to:

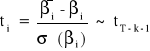
i = 0, 1, ..., k

Z własności rozkładu t - studenta wynika, że:

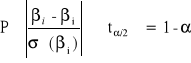
co daje:

Interpretacja:

Z prawdopodobieństwem 1 - α przedział o podanych końcach zawiera nieznaną wartość parametru strukturalnego β_i.

Jak widzimy przedział ufności może mieć różną szerokość.

Przedział ufności jest dobry, czyli wąski, ponadto nie zawiera zera.

Szerokość przedziału ufności zmniejsza się jeżeli:

• jest niska wartość wariancji resztowej;

• nie występuje zależność pomiędzy zmiennymi objaśniającymi.

Testy jednostronne:

1. Lewostronny:

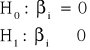
W takim przypadku obszar krytyczny konstruowany jest następująco:

- 1,75 0,00

2. Prawostronny:

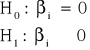
W takim przypadku obszar krytyczny konstruowany jest następujuąco:

Graficzną prezentacją tak zbudowanego obszaru krytycznego jest obszar położony na prawo od wartości t_α:

0,00 1,75

Testowanie indywidualnej istotności parametrów strukturalnych (test t - studenta):

H₀ : β_i = 0 parametr strukturalny jest nie istotnie różny od zera, czyli zmienna objaśniająca X_ti nie istotnie wpływa na zmienną objaśnianą. Hipoteza niekorzystna.

H₀ : β_i ≠ 0 Parametr strukturalny jest istotnie różny od zera, czyli zmienna objaśniajaca X_ti Istotnie wpływa na zmienną objaśnianą.

Weryfikacje hipotez:

Statystyka testu ma postać:

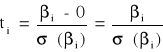
i = 0, 1, ..., k

o rozkładzie t - studenta (T - k - 1) stopniach swobody.

t_i ~ t_{T - k - 1}

Reguły podejmowania decyzji:

odrzucamy H₀ na rzecz H₁

nie ma podstaw do odrzucenia H₀

Wartości krytyczne statystyki t są odczytywane z tablic rozkładu t - studenta dla T - k - 1 stopni swobody i poziomu istotności α.

- t_α/2 t_α/2

3,50 -1,75 0,00 1,75 3,50

odrzucamy przyjmujemy odrzucamy

H₀ H₀ H₀

Badanie łącznej istotności parametrów:

H₀ : β* = 0 gdzie β* = [β₁, β₂, ..., β_k]

Parametry strukturalne łącznie są nie istotnie różne od zera, czyli zmienne objaśniające łącznie, nieistotnie wpływają na zmienną objaśnianą.

H₁ : mówi, że nie wszystkie z wymienionych parametrów są równe zeru (korzystne).

Statystyką testu, jest statystyka, która przy założeniu prawdziwości hipotezy zerowej ma rozkład F. Fishera - Sendykora z (k, T - k - 1) stopniami swobody.

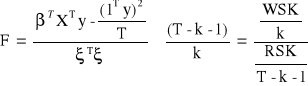
Reguła decyzyjna:

odrzucamy H₀

nie ma podstaw do odrzucenia H₀

Weryfikacja składnika losowego modelu.

Autokorelacja (przenoszenie oddziaływania składnia losowego z okresu na okres) składników losowych.

Założenie stochastyczne modelu implikuje brak skorelowania składników losowych w czasie.

Jeżeli nie jest ono spełnione to:

gdzie t ≠ s

Jeśli składniki losowe z dwóch sąsiednich okresów są ze sobą skorelowane, czyli:

gdzie ε_t - błąd czysto losowy

Jeżeli:

ρ₁ = -1 to w modelu występuje autokorelacja ujemna składników losowych I - rzędu; sytuacja niekorzystna;

ρ₁ = 0 to w modelu nie występuje autokorelacja składników losowych; sytuacja korzystna;

ρ₁ = 1 to w modelu występuje autokorelacja dodatnia składników losowych I - rzędu.

Przyczyny wywołujące autokorelację składników losowych w modelu ekonometrycznym są następujące:

1. Naturalne - następuje zakłócenie w normalnym przebiegu zjawiska, czyli okres przyjęty za jednostkę obserwacji jest krótszy niż czas działania czynników przypadkowych (tzw. autokorelacja czysta).

2. Błędy w budowie modelu powodujące autokorelację:

1. dodatnią:

• przyjęcie niewłaściwej postaci analitycznej (np. zamiast potęgowej szacujemy liniową);

• pominięcie jednej lub kilku istotnych zmiennych;

• powolne wygasanie efektów składnika losowego;

• przyjęcie niewłaściwych opóźnień przy zmiennych;

• niesystematyczny rozkład zmiennej losowej.

2. ujemną:

• przepełnienie modelu zmiennymi;

• nieuwzględnienie występowania cyklu dwuokresowego.

Sposoby eliminacji autokorelacji:

• rozpoznanie przyczyn autokorelacji oraz zmiana konstrukcji modelu;

• zmiana skali zmiennych ekonomicznych;

1. w przypadku autokorelacji dodatniej:

• dołączenie nowej zmiennej objaśniającej;

• wprowadzenie dynamiki do modelu;

• dołączenie zmiennej zerojedynkowej;

• zmiana postaci analitycznej modelu.

2. w przypadku autokorelacji ujemnej:

• usunięcie zmiennej (zmiennych) objaśniającej;

• dołączenie zmiennej cyklicznej dwuokresowej.

Skutki skorelowania składników losowych w czasie:

1. Wariancja resztowa daje zbyt wysokie wartości wskaźnika dopasowania modelu.

2. Elementy macierzy wariancji i kowariancji są niedoszacowane.

3. Wnioskowanie na podstawie istotności nie może być interpretowane jako właściwe.

Jeżeli mamy model autoregresji I - rzędu oraz spełnione są założenia:

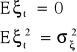
wówczas współczynnik autoregresji I - rzędu jest równy współczynnikowi autokorelacji:

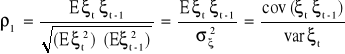
Oceną składnika losowego (ξ_t) jest składnik resztowy
.

Gdy składniki losowe podlegają schematowi autoregresyjnemu I - rzędu to ocena parametru ρ powinna być istotna statystycznie. Ocenę tę otrzymujemy ze wzoru:

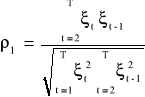
Ocena ta jest nazywana współczynnikiem autokorelacji reszt, który informuje o sile i kierunku skorelowania reszt modelu i jest on przybliżoną miarą współczynnika autokorelacji składników losowych.

Założenia:

1. Model jest liniowy.

2. W modelu występuje wyraz wolny.

3. W modelu nie występuje zmienna endogeniczna opóźniona o jeden okres.

Jeżeli powyższe założenia zostaną spełnione to stosujemy:

Test Durbina - Watsona (DW).

Układ pierwszy testujący występowanie autokorelacji dodatniej:

autokorelacja składników losowych I - rzędu nie występuje

autokorelacja dodatnia

Układ drugi testujący występowanie autokorelacji ujemnej:

autokorelacja składników losowych I - rzędu nie występuje

autokorelacja ujemna

Aby zweryfikować powyższe hipotezy oblicza się statystykę Durbina - Watsona:

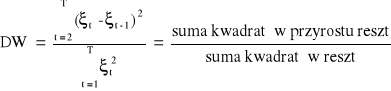
Istnieje pewien przybliżony związek między wartości DW a współczynnikiem autokorelacji reszt I - rzędu:

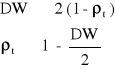
DW = 2 (1 - (-1)) = 4

DW = 2 (1 - 0) = 2

DW = 2 (1 - 1) = 0

ρ1	- 1	↑	0	↑	1
DW	4	↓	2	↑	0

Statystyka DW jest w przybliżeniu malejącą funkcją współczynników autokorelacji reszt I - rzędu.

Jeżeli
to autokorelacja nie występuje.

Zakładamy, że dla takich wartości testu DW autokorelacja składników losowych I - rzędu nie występuje.

Z tablic DW odczytujemy wartości krytyczne (α, k + 1, T).

d_L - wartość dolna

d_U - wartość górna

d_L < d_U

Reguła decyzyjna:

Dla 0 ≤ DW < 2 testujemy występowanie autokorelacji dodatniej:

1. DW < d_L

2. d_L < DW < d_U - obszar martwy testu. Test nie rozstrzyga czy w modelu występuje autokorelacja.

3. DW > d_U - nie ma podstaw do odrzucenia H₀. W modelu autokorelacja nie występuje.

Jeżeli 2 < DW ≤ 4 (wówczas testujemy występowanie autokorelacji ujemnej) należy obliczyć DW ze wzoru:

DW' = 4 - DW

1. DW' < d_L

2. d_L < DW' < d_U

3. DW' > d_U

Badanie normalności rozkładu składników losowych.

Test Jarque'a Bera (J - B).

Weryfikujemy następujące hipotezy:

składnik losowy ma rozkład normalny

składnik losowy nie ma rozkładu normalnego

Do weryfikacji wykorzystujemy statystykę Jarque'a Bera:

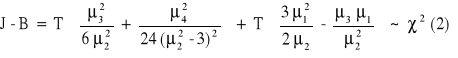
J - B = (0, +∞)

gdzie:

oznacza j - ty moment zwykły w populacji

Obszar krytyczny prawostronny.

Reguła decyzyjna:

odrzucamy H₀ na rzecz H₁, hipoteza niekorzystna

nie ma podstaw do odrzucenia H₀, hipoteza korzystna

Testowanie stałości wariancji składników losowych.

Test White'a.

Testowane są hipotezy zmienności wariancji składników zakłócających modelu:

Homoskedastyczność - stałość wariancji składnika losowego w czasie.

Hederoskedastyczność - brak stałości wariancji składnika losowego w czasie.

X₁ X₂ X_n X₁ X₂ X_n

Poddajemy weryfikacji następujące hipotezy:

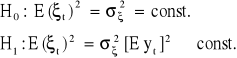
Test White'a jest oparty na dodatkowej regresji kwadratów reszt
:

Po oszacowaniu parametrów modelu KMNK weryfikujemy hipotezę, że parametr α₁ = 0 na rzecz hipotezy alternatywnej, że α₁ ≠ 0.

Statystyka testu White'a ma rozkład:

1. dla dużych prób (> 30):
   ;

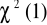
2. dla małych prób (< 30):
   .

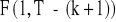
Obszar krytyczny prawostronny.

Reguła decyzyjna:

1. dla dużych prób:

odrzucamy H₀

nie ma podstaw do odrzucenia H₀

2. dla małych prób:

odrzucamy H₀

nie ma podstaw do odrzucenia H₀

Heteroskedastyczność rozkładu składnika losowego.

Test Goldfelda - Quandta (F_GQ).

Zakładamy, że ciąg reszt modelu może zostać podzielony na dwie części (niekoniecznie równe). Założenie to znajduje odzwierciedlenie w zestawie hipotez testu:

wariancje rozkładów składnika losowego w obu próbach są takie same

wariancje rozkładów różnią się

Wyznaczamy statystykę w zależności od liczebności podzielonych prób:

Jeżeli RSK₁ > RSK₂:

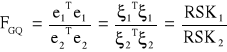
Statystyka:

Jeżeli RSK₂ > RSK₁:

Reguła decyzyjna:

Obszar krytyczny prawostronny.

odrzucamy H₀ na rzecz H₁

nie ma podstaw do odrzucenia H₀

Programowanie liniowe.

Zagadnienie programowania liniowego to szczególny przypadek zagadnienia programowania matematycznego, w którym wszystkie związki zachodzące między zmiennymi mają charakter liniowy.

Metody programowania liniowego pozwalają na określenie optymalnej alokacji ograniczonych zasobów czynników.

Do podstawowych problemów rozwiązywanych metodami programowania liniowego należą m.in.:

• wybór odpowiedniego asortymentu produkcji;

• problem mieszanek (mieszanka i dieta, np. dwie różne farby - grosza i lepsza);

• zagadnienia transportowe;

• zagadnienia kolejek;

• analiza sieciowa (podczas gotowania możemy skrócić czas poprzez robienie czynności równolegle).

Istnieją dwie metody rozwiązywania zadań programowania liniowego:

1. Metoda geometryczna (dwie zmienne decyzyjne).

2. Metoda algorytmiczna (posługująca się algebrą liniową).

Ogólna postać liniowego modelu decyzyjnego:

Jeżeli oznaczymy:

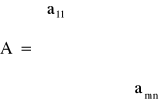
Macierz warunków

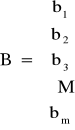
Wektor ograniczeń

m - ile ograniczeń (np. liczba surowca)

n - ile poszczególnych rodzajów zmiennych decyzyjnych (np. dwa rodzaje butów)

A - macierz współczynników technologicznych

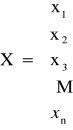
Wektor zmiennych decyzyjnych (ile składników)

To zagadnienie programowania liniowego można zapisać następująco:

Liniowy model decyzyjny:

Postać kanoniczna:

Warunki wewnętrznej zgodności funkcji celu - układ ograniczający funkcję celu w formie nierówności lub równości - nie może być ani więcej ani mniej surowców, np. gwoździ do mebli.

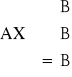
≤ B - optymalna struktura produkcji

≥ B - dieta lub mieszanka

= B

X ≥ 0 - warunki brzegowe nałożone na zmienne decyzyjne (np. nie może być ujemnych ilości butów)

Z (X) = CX - funkcja celu (optimum)

Metoda geometryczna rozwiązywania zagadnienia programowania liniowego:

W modelu występują dwie zmienne decyzyjne:

y₂

x₁

Twierdzenie 1:

Zbiorem wypukłym W c R_n nazywamy taki zbiór, w którym odcinek łączący dwa dowolne punkty należy do zbioru W.

zbiór wypukły odcinek nie należy do zbioru,

więc nie jest wypukły

Twierdzenie 2:

Zbiór D rozwiązań dopuszczalnych liniowego modelu decyzyjnego jest zbiorem wypukłym.

Warunki ograniczające tworzą zbiór rozwiązań dopuszczalnych (LMD - liniowy model decyzyjny).

Twierdzenie 3:

Funkcja celu osiąga wartość optymalną w wierzchołku zbioru wypukłego D utworzonego z rozwiązań dopuszczalnych liniowego modelu decyzyjnego.

y₂

l₁

l₂

x₁

Wypukły zbiór rozwiązań dopuszczalnych T₁ i T₂. Zgodnie z Twierdzeniem 3 o wartości optymalnej podejrzane są punkty wierzchołkowe. Rozwiązanie optymalne znajduje się w jednym z tych punktów wierzchołkowych.

l₁ l₂

Nieograniczony zbiór rozwiązań dopuszczalnych jest wypukły. Funkcja minimalizowana będzie miała określone optimum.

l₁ l₂

Nie jest to zbiór rozwiązań dopuszczalnych, lecz zagadnienie sprzeczne, nie da się rozwiązać.

Zbiór rozwiązań dopuszczalnych to punkt wspólny.

Twierdzenie 4:

Jeżeli istnieją co najmniej dwa rozwiązania optymalne, to każda liniowa kombinacja wypukła tych rozwiązań jest także rozwiązaniem optymalnym danego modelu decyzyjnego.

l₁ l₂

Zbiór rozwiązań jest dopuszczalny. Gdy w dwóch punktach otrzymamy taką samą wartość celu (najmniejszą lub największą).

Schemat programowania liniowego:

1. Określenie:

1. Funkcji celu (maksymalny zysk czy minimalny koszt).

2. Warunków wewnętrznej zgodności funkcji celu.

3. Warunków brzegowych.

2. Wyznaczenie obszaru rozwiązań dopuszczalnych.

3. Wyznaczenie rozwiązania optymalnego.

Dualizm.

Zgodnie z zasadą racjonalnego gospodarowania można rozpatrywać alternatywne rozwiązania:

1. Maksymalizacja efektów przy określonym poziomie nakładów.

2. Minimalizacja kosztów przy określonym poziomie produkcji.

Zasady sprowadzania modelu prymalnego do dualnego:

1. W modelu dualnym występują zmienne decyzyjne „U”.

2. Zmiennych dualnych jest tyle, ile zasadniczych warunków ograniczających w modelu pierwotnym.

3. Ilość warunków ograniczających w modelu dualnym jest równa ilości zmiennych decyzyjnych w modelu prymalnym.

4. Znak nierówności jest podporządkowany kryterium optymalizacji.

Jeżeli jeden ze znaków jest równością (=) wówczas zmienna dualna „U”, która mu odpowiada może mieć dowolny znak (może być ujemna).

5. Wartościami ograniczeń w modelu dualnym są współczynniki funkcji celu w modelu prymalnym.

6. Współczynniki funkcji kryterium modelu dualnego są wartościami ograniczeń w modelu prymalnym.

Zapis modelu:

1. prymalnego:

max Z (X) = C ^T X

AX ≤ B

X ≥ 0

2. dualnego:

min W (U) = B ^T U

A ^T U ≥ C

U ≥ 0

Twierdzenia:

1. Jeżeli model dualny ma rozwiązania to ma je również rozwiązanie pierwotne.

2. Jeżeli model dualny ma rozwiązanie optymalne to wartość funkcji celu modelu pierwotnego i dualnego są takie same.

3. Jeżeli model pierwotny (dualny) ma nieograniczone optimum to model dualny (pierwotny) ma sprzeczny układ warunków ograniczających.

Jeżeli mamy n - zmiennych decyzyjnych to mówimy o metodzie Simplex.

Metoda Simplex:

Niech dany będzie model decyzyjny (postać strukturalna):

max Z (X) = C ^T X

AX ≤ B

X ≥ 0

Metoda Simplex - jest to algebraiczna metoda rozwiązywania zagadnień programowania liniowego. Rozwiązanie optymalne zagadnienia programowania liniowego odpowiada przynajmniej jednemu z wierzchołków zbioru rozwiązań dopuszczalnych.

Metoda polega na iteracyjnym (krokowym) przechodzeniu z wierzchołka do wierzchołka, aż otrzyma się rozwiązanie optymalne (wybiera się ten kierunek, który jest najkrótszy).

Etapy rozwiązywania zagadnienia za pomocą metody Simplex:

1. Doprowadzenie postaci kanonicznej modelu:

do postaci standardowej:

S_i - zapas (zmienna dodatkowa)

lub zamiana

na

S_i - zmienna niedoboru lub nadmiaru (zmienna dodatkowa)

Zmienne „S” w funkcji celu mają współczynniki równe zeru. W wyjaśnionym rozwiązaniu tworzą bazę, dlatego nazywamy je zmiennymi bazowymi. Zmienne bazowe są równe wyrazom wolnym, a zmienne nie bazowe są równe zero. Jeżeli zmienna „S” jest bazowa, to X₁ i X₂ są zmiennymi nie bazowymi.

2. Zapis zagadnienia w postaci tablicy, która zawiera wszystkie informacje o danym zadaniu.

Baza	Cj	X1	X2		Xm	S1		Sn	b1
				C1	C2		Cm	0				0
S1	0	a11	a12		a1m	1		0	b1
S2	0	a21	a22		a2m	0		0	b2
Sn	0	an1	an2		anm	0		1	bn
Cj - Zj						0		0	0
BIG M		0	0		0	0	0	0	0

Wartość funkcji celu dla danego rozwiązania bazowego.

Rozwiązanie bazowe to:

X₀ = [0, ..., 0; b₁, ..., b_m] X = [X₁, X₂, ..., X_n; S₁, S₂, ..., S_n]

gdzie:

X₁ = 0, ..., X_n = 0; S₁ = b₁, ..., S_n = b_n

3. Określenie czy otrzymane rozwiązanie jest rozwiązaniem optymalnym (iteracja).

4. Iteracji dokonuje się tak długo, aż wskaźniki optymalności przyjmą wartości niedodatnie. Natomiast w przypadku minimalizacji wskaźniki te muszą być nieujemne.

Wskaźniki te oblicza się jako:

5. Wybór elementu rozwiązującego:

• wybór kolumny rozwiązującej - kolumny, która charakteryzuje się największym dodatnim współczynnikiem C_j - Z_j, czyli:

max (C_j - Z_j > 0)

• dla ustalonej kolumny szuka się najmniejszego z nieujemnych stosunków:

min

W ten sposób ustala się element rozwiązujący. Do bazy trafia zmienna, w której kolumnie jest element rozwiązujący.

Przechodząc do następnej tablicy dokonuje się przekształceń Jordana:

• elementy w wierszu rozwiązującym dzieli się przez element rozwiązujący;

• elementy w kolumnie rozwiązującej są zamieniane na zera, prócz elementu rozwiązującego;

• pozostałe elementy nie znajdujące się ani w wierszu, ani w kolumnie rozwiązującej oblicza się ze wzoru:

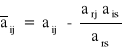
i ≠ r, j ≠ s

r - wiersz rozwiązujący

s - kolumna rozwiązująca

A₁ - zmienna sztuczna A

A - zmienna sztuczna

M - współczynnik w funkcji celu, który jest bardzo dużą liczbą dodatnią

Zmienne „A” nie mają interpretacji ekonomicznej, a więc nie mogą znaleźć się w rozwiązaniu optymalnym.

Każdej zmiennej A_i przypisujemy dużą wartość współczynnika kary oznaczonego przez „M”.

W przypadku, gdy zmienna sztuczna znajduje się w rozwiązaniu bazowym, wówczas wartość celu zwiększa (zmniejsza) się o MA.

Model transponowany.

Podstawowe założenia modelu transponowanego:

• liczba odbiorców i dostawców jest ustalona;

• należy dostarczyć jednorodny produkt;

• znana jest podaż każdego dostawcy i popyt każdego odbiorcy na dany produkt w danym okresie;

• ustalone są koszty jednostkowe transportu produktu;

• koszty jednostkowe transportu pomiędzy dostawcami i odbiorcami są proporcjonalne do przewożonego produktu;

• minimalizowane są łączne koszty przewozu ze względu na odległość;

• wyróżnia się następujące typy odległości:

1. odległość ekonomiczno - taryfowa;

2. odległość komunikacyjna;

3. odległość czasowa.

• odległość ekonomiczno - taryfową i komunikacyjną opisują liniowe modele decyzyjne, natomiast odległość czasową - modele sieciowe.

Podstawowe oznaczenie:

Dostawcy - D_i, gdzie i = 1, 2, ..., m

Odbiorcy - O_j, gdzie j = 1, 2, ..., n

Ilość produktów, które należy dostarczyć (podaż):

a_i (i = 1, 2, ..., m)

Zapotrzebowanie (popyt):

b_j (j = 1, 2, ..., n)

Macierz przepływów X = (x_ij) - zmienne decyzyjne, które informują ile towaru przewozimy od i - tego dostawcy do j - tego odbiorcy.

Macierz odległości C = (c_ij)

Wektor podaży A = [a_i]

Wektor popytu B = [b_j]

Tabela transportowa:

	O1	O2		On	O0
D1	C11 X11	C12 X12		C1n X1n	a1
D2	C21 X21	C22 X22		C2n X2n	a2
Dm	Cm1 Xm1	Cm2 Xm2		Cmn Xmn	am
D0	b1	b2		bn

Istota modelu transportowego polega na wyznaczaniu takiej macierzy przypływów masy towarowej od dostawców do odbiorców, aby zminimalizować funkcję kryterium.

W przypadku, gdy łączna podaż równa się łącznemu popytowi dane zagadnienie nazywamy zbilansowanym lub zamkniętym. W przeciwnym wypadku zagadnienie jest niezbilansowane lub otwarte.

W celu rozwiązania zagadnienia transportowego dane zagadnienie musi być zbilansowane. Aby model zbilansować wprowadza się fikcyjnego odbiorcę, jeżeli:

lub fikcyjnego dostawcę, jeżeli:

Model matematyczny zagadnienia transportowego przedstawia się następująco:

dla i = 1, 2, ..., m

dla j = 1, 2, ..., n

dla każdego i, j

Dwa etapy:

1. Wyznaczenie rozwiązania dopuszczalnego.

2. Wyznaczenie rozwiązania optymalnego (metoda potencjałów).

Zagadnienie transportowe można rozwiązań metodą Simplex, lecz istnieją inne bardziej efektywne metody.

W celu otrzymania rozwiązania dopuszczalnego można wykorzystać:

• metodę kąta północno - zachodniego;

• metodę minimalnego elementu macierzy;

Jeżeli ... rozwiązanie dopuszczalne za pomocą tej metody rozdysponujemy wszystkie środki wówczas otrzymane rozwiązanie jest optymalne.

• metodę minimalnego elementu wiersza;

• metodę minimalnego elementu kolumny;

• metodę aproksymacji Vogla.

Jeżeli istnieje potrzeba poprawy danego rozwiązania należy posłużyć się iteracyjną metodą potencjałów.

Twierdzenie:

Jeżeli dane są dwa zagadnienia transportowe o tych samych wektorach podaży i popytu oraz odpowiadające im macierze odległości

dla i = 1, 2, ..., m j = 1, 2, ..., n

spełniających warunek:

gdzie:

r, u_i, v_j, u_i, v_j - dowolne liczby rzeczywiste

i = 1, 2, ..., m; j = 1, 2, ..., n - to rozwiązanie optymalne jednego zagadnienia jest rozwiązaniem optymalnym drugiego zagadnienia.

Metoda potencjałów.

Składa się z następujących elementów:

• wyznacza się wyjściowe rozwiązanie bazowe (dopuszczalne);

• sprawdza się czy uzyskane rozwiązanie jest rozwiązaniem optymalnym, jeśli tak to procedura kończy się, jeżeli nie to przechodzi do kolejnego etapu;

• ustala się trasę centralną i poprawia poprzednie rozwiązanie, a następnie wraca do etapu drugiego.

Trasa centralna służy do generowania nowego rozwiązania. Trasa centralna <k, l> tworzy wraz z elementami zbioru B cykl C_kl, czyli drogę zamkniętą, która:

• ma parzystą liczbę tras;

• dokładnie dwa elementy w każdym wierszu i kolumnie, przez który przechodzi.

Trasy, które tworzą cykl C_kl oznacza się na przemian znakami „+” i „-”. Trasa ze znakiem „+” zwiększa przewozy, a ze znakiem „-” zmniejsza. Następnie wśród tras zmniejszających przewozy wybiera się tę, która jest minimalna.

Kryterium optymalności.

Otrzymane rozwiązanie jest rozwiązaniem optymalnym, jeżeli wartości wszystkich wskaźników optymalności są ujemne. Jeżeli choć jeden ze wskaźników optymalności jest ujemny to istnieje możliwość poprawy uzyskanego rozwiązania.

Kryterium wejścia.

W macierzy wskaźników optymalności szuka się najmniejszego elementu, a następnie odpowiadającą mu zmienną wprowadza się do bazy.

Kryterium wyjścia.

Bazę opuszcza ta zmienna, dla której trasa zmniejszająca koszty jest najmniejsza.

Nowe rozwiązanie otrzymuje się zwiększając współrzędne dotychczasowego rozwiązania na trasach dodatnich o znalezioną minimalną wartość oraz zmniejszając składowe dla węzłów ujemnych części tras.

---