Ekonomia Matematyczna

Równania różniczkowe i niektóre ich zastosowania ekonomiczne

W równaniach tych poszukujemy funkcji:

1. Równania różniczkowe zwyczajne w równaniach tych poszukujemy funkcji jednej zmiennej. Ogólna postać takiego równania (równanie nr.1)
gdzie F jest daną funkcją n+1 argumentów. Poszukujemy funkcji y= f(x). Liczbę n nazywamy rzędem równania.

1. Równania różniczkowe zwyczajne rzędu pierwszego. Postać
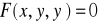
   (równanie nr 2) Poszukujemy różniczkowej funkcji y= f(x) .Każdą taką funkcję spełniającą równanie ( nr 2) nazywamy rozwiązaniem lub całką równania. Jeżeli z równania (nr 2) można wyznaczyć y' tzn. y'= f (x,y) ( równanie nr 3) a funkcja f(x,y):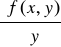
   są ciągłe w pewnym płaskim otoczeniu punktu (x₀,y₀) to przez ten punkt przechodzi dokładnie jedna krzywa całkowa y=f(x) y₀=f(x₀)

1.1.1 Równanie o zmiennych rozdzielonych

lub

Równanie „zakażenia „

B - liczba osób w populacji

Y(t) - funkcji różniczkowej ( dla
) której wartości całkowite dodatnie oznaczają liczbę osób „zakażonych „ w chwili+

- ( równanie nr 4) ay - zakażeni

( b-y) liczba osób nie zakażonych

a - stała dodatnia po całkowaniu

(B-A)=0

b=

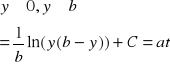
Równanie ( nr 4) jest przykładem pewnego nieliniowego równania zwyczajnego rzędu pierwszego.

2. Równania różniczkowe liniowe

Podstawowe metody całkowania

1. Metoda przewidywań

2. metoda uzmienniania stałej

3. metoda czynnika całkującego prowadząca do wzoru
   

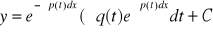
przykład : y - funkcja „ dochód „ y

I - funkcja inwestycji ( stały udział inwestycji w dochodzie ).

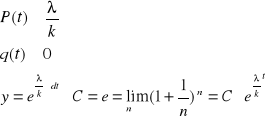
- zwany stopą wzrostu dochodu w rachunku Kaleckiego np. gdy λ=0,2 , k=3

Poziomy stacjonarne procesów.

Jeżeli proces może być opisany za pomocą równania różniczkowego rzędu i-go o stałych współczynnikach to stacjonarne poziomy procesu znajdujemy z równania
jeżeli opis procesu
równanie y^˚=0 oznacza że poszukujemy rozwiązań równania f(y)=0

Przykład : załóżmy, że proces opisuje równanie y˚=y²-5y+6=0 są dwa poziomy stacjonarne y^'₁=3,y₂=2

Przykład 2: Proces zakażenia :y˚=ay(b-y)=0

Y=0 interpretujemy że nikt się nie zarazi

Y=b wszyscy się zakażą

Model eskalacji wydatków budżetowych ( np. na zbrojenia )

X=x(t) - funkcja wydatków budżetowych na zbrojenia w systemie I

Y=y(t) - funkcja wydatków na zbrojenia w systemie II

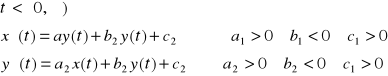
jest to układ dwóch równań różniczkowych różniczkowych z dwiema niewiadomymi funkcjami

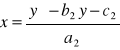
podstawiając do równania I-go równania otrzymamy równanie różniczkowe rzędu II-go względem Y.

Metoda rozwiązywania równań różniczkowych zwyczajnych rzędu II-go o stałych współczynnikach. Rozważania ograniczamy do rozważań liniowych postaci

Rozwiązania poszukujemy w postaci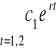

Równanie charakterystyczne jest następujące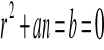
jest to równanie kwadratowe jeśli Δ>0 to są dwa rzeczywiste rozwiązania r₁,r₂ . Znaleziona funkcja
gdzie stałe c₁,c₂ wyliczamy mając dwa warunki początkowe.

Y(0)=y₀ - konkretna liczba

Y(1)=y₁

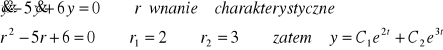
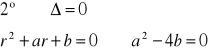
istnieje wtedy jeden dwukrotny pierwiastek r_1,2 rozwiązanie y=(c₁+c₂)^e

3˚ Δ=a²-4b<0

wtedy równanie charakterystyczne posiada dwa pierwiastki nierzeczywiste

r₁=ά-iβ r₂=α+iβ gdzie αβ zależą od stałych a i b

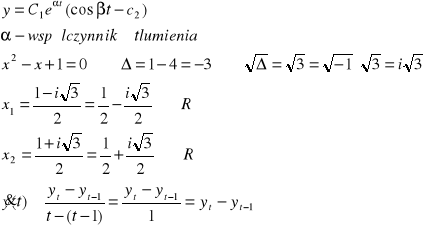
W analizie numerycznej do obliczeń stosuje się właśnie ten wzór przybliżony

Podobnie konstruuje się wzory zwrotne wyrażające
za pomocą pochodnych.

Y=Y(t) - różniczkowa funkcja zmiennej t> 0

W analizie różniczkowej posługujemy się wielkościami Y(t),Y(t-1), Y(t-2). Rozważmy równanie różniczkowe I rzędu o stałych współczynnikach
sosunek ten nazywa się dynamiką Y pomiędzy chwila t-1 a t . Natomiast
tempo wzrostu Y (analogiem tego pojęcia jest
- stopa wzrostu ).

Analityczne pojęcie problemu stanów stacjonarnych procesów dających się opisać za pomocą równań różnicowych G(Yt,Yt-1)=0 to stan stacjonarny jeśli istnieje znajdujemy z równania G(g,g…)=0

nie ma stanów stacjonarnych

1. Geg yt jest rosnący powód załóżmy że y1>y₀ gdyż
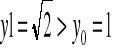
   załóżmy że dla pewnego t>1 yt>yt-1 wtedy yt+1=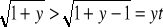
   

2. ciąg yt jest ograniczony z góry ( przez liczbę 2)
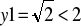
   załóżmy że dla pewnego t>1 yt<2 wtedy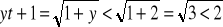
   ciąg yt jest więc bieżny ( jako rosnący i ograniczony )

Niech
do rozwiązania

Dla równania różniczkowego liniowego rzędu I postaci yt+ay-1=0 yt=Ar⁺ gdzie A dowolna stała

r- pierwiastek równania charakterystycznego powstałego z rozwiązania znajdujemy

Równanie postaci Yt=A(-a)^t

Równanie różniczkowe rzędu II

otrzymujemy równanie charakterystyczne

r²+ar+b=0

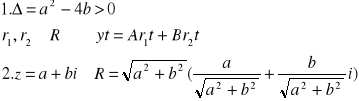
Postać trygonometryczna liczb zespolonych

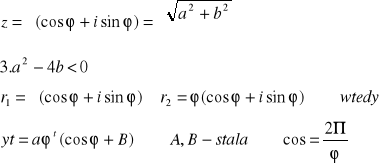
Model Samuelana Hiltera

( y- produkcja, zt - popyt globalny)

Zt=I_t+ Ct ( I- inwestycje, Ct- konsumpcje )

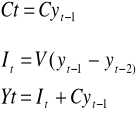
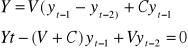
współczynnik kapitałowości inwestycji

---